北京师大附中2020-2021学年下学期高一年级期末考试数学试卷
本试卷有三道大题，考试时长120分钟，满分150分。
一、选择题（每小题4分，共40分，每题均只有一个正确答案）
1. 若sinα＜0，且cosα＞0，则角α是
A. 第一象限角 B. 第二象限角 C. 第三象限角 D. 第四象限角
2. 已知正方形ABCD的边长为1，则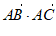
＝
A.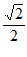 
B. 1 C. 
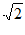D. 2
3. 圆锥的母线长为5cm，底面半径为2cm，则圆锥的侧面积为
A. 20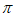
cm2 B. 10
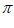cm2 C. 28
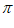cm2 D. 14
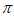cm2
4. 已知向量a＝（-1，3），b＝（x，-1），a⊥b，则x的值是
A. 3 B.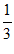 
C. -3 D.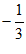 
5. 如图，四边形ABCD是正方形，PA⊥平面ABCD，且PA＝AB，则直线PB与直线CD所成角的大小是
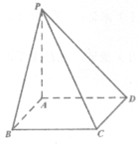
A. 30° B. 45° C. 60° D. 90°
6. 函数y＝2sin（x–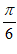
）的图象
A. 关于直线x＝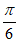
对称 B. 关于直线x＝–
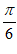对称
C. 关于点（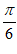
，0）对称 D. 关于点（–
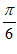，0）对称
7. 在△ABC中，a＝2bcosC，那么这个三角形是
A. 等边三角形 B. 等腰三角形 C. 直角三角形 D. 不确定
8. 如图，在长方体ABCD-A1B1C1D1中，若E，F，G，H分别是棱A1B1，BB1，CC1，C1D1的中点，则下列结论一定成立的是
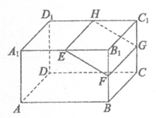
A. 四边形EFGH是矩形 B. 四边形EFGH是正方形
C. BD∥HG D. 平面EFGH∥平面ABCD
9. 已知平面向量a，b满足|a|＝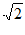
，|b|＝1，则“a–b与a＋2b互相垂直“是“a⊥b“的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
10. 如图，函数y＝2sin（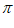
x＋
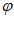）（0＜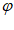
≤
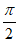）在一个周期内的图象与y轴交于点（0，1）。P是其图象上的最高点，M、N是其图象与x轴的交点，则
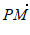与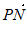
的夹角的余弦值为
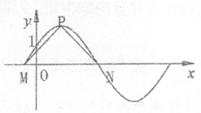
A. 0 B.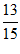 
C. 
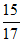D. 1
二、填空题（每小题5分，共25分）
11. 在△ABC中，B＝30°，AB＝15，BC＝5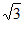
，则AC＝_______。
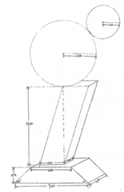
12. 如图，这个组合体是小张同学自己设计的一个小奖杯，计划送给小刘同学，以鼓励其认真努力的学习数学，已知该奖杯中的四棱柱的高为10cm，底面是长和宽分别为3cm、2cm的矩形，则该四棱柱的体积是________cm3；奖杯顶部两个球的半径分别为5cm和2cm，则这两个球的表面积之和为________cm2。
13. 我国魏晋时期的数学家刘徽在给《九章算术》作注时，想到了推算球体积的方法，创造了一个称为“牟合方盖“的立体图形。如图1所示，在一个正方体内作两个互相垂直的内切圆柱，其相交的部分，就是牟合方盖，如图2所示，牟合方盖恰好把正方体的内切球包含在内并且同球相切，刘徽指出，球体积与牟合方盖体积之比等于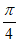
，若正方体的棱长为2，则“牟合方盖“的体积等于_________。
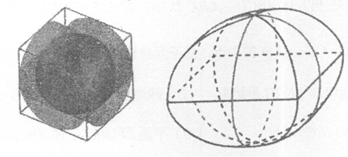
图1 图2
14. α和β是两个不同的平面，m和n是平面α及β外的两条不同直线，给出四个论断：
①m⊥n ②α⊥β ③n⊥β ④m⊥α
以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题：________。
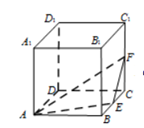
15. 如图，在棱长为1的正方体ABCD-A1B1C1D1中，点E，F分别是棱BC，CC1的中点，P是侧面BB1C1C内一点，若A1P∥平面AEF，则下列说法正确的是________。
①线段A1P的最大值是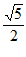
②A1P⊥B1D
③A1P与DE一定异面
④三棱锥B-A1PC1的体积为定值
（注：全部正确得5分，有漏选得3分，有错选或不选得0分）
三、解答题（共6小题，共85分。解答时写出文字说明，演算步骤或证明过程）
16. （本小题14分）
在△ABC中，b＝2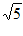
，A＝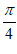
，cosB＝
。
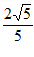（I）求a的值；
（Ⅱ）求△ABC的面积。
17. （本小题12分）
在正方体ABCD-A1B1C1D1中，E为CC1中点。
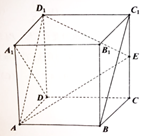
（I）求证：BC1∥平面AD1E；
（Ⅱ）求证：A1D⊥平面ABC1D1。
18. （本小题14分）
已知函数f（x）＝（2cos2x-1）sin2x＋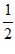
cos4x。
（I）求f（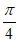
）；
（Ⅱ）求f（x）的最小正周期；
（III）求f（x）在区间（0，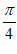
）上的最大值。
19. （本小题15分）
在△ABC中，sin2B＋sin2C-sin2A＝sinBsinC。
（I）求A的值；
（Ⅱ）再从条件①、条件②、条件③这三个条件中选择两个作为已知，求BC边上的中线AD的长度。
条件①：b＝8；条件②：S△ABC＝10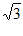
；条件③：cosB＝
。
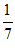注：如果选择多组条件分别解答，按第一个解答计分。
20. （本小题15分）
已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB＝90°，PA⊥平面ABCD，且PA＝AD＝DC＝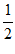
AB＝1，M是棱PB上的动点。
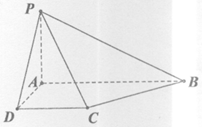
（I）求证：平面PAD⊥平面PCD；
（Ⅱ）若PD∥平面ACM，求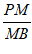
的值；
（Ⅲ）当M是PB中点时，设平面ADM与棱PC交于点N，求截面ADNM的面积。
21. （本小题15分）
已知集合Sn＝｛X｜X＝（x1，x2，…，xn），xi∈R，i＝1，2，…，n｝，称xi为X的第i个分量，对于Sn的元素A＝（a1，a2，…，an），B＝（b1，b2，…，bn），定义A与B的两种乘法分别为：
A×B＝（a1b2– a2b1，a2b3– a3b2…，anb1– a1bn），
A*B＝（a1a2＋b1b2，a2a3＋b2b3…，ana1＋bnb1）。
给定函数f（x），定义Sn上的一种变换F（X，f）=（f（x1），f（x2），…，f（xn））。
（I）设f（x）＝|x|，A＝（1，0，-1），B＝（-1，0，1），求F（A，f）×F（B，f）和F（A，f）*F（B，f）；
（Ⅱ）设f（x）＝sinx，g（x）＝cosx，对于X=（x1，x2，…，xn），设A0＝F（X，f），B0＝G（X，g）。对任意k∈N且k≤n-1，定义Ak+1＝Ak×Bk，Bk＋1＝Ak*Bk。
（i）当n＝3时，求证：A2中为0的分量个数不可能是2个；
（i）若X＝（x1，x2，…，xn）的任一分量都只能取x或-x，设An-1的第1个分量为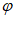
（x），求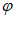
（x）的最小正周期的最小值，并求出此时所有的X。
参考答案
一、选择题（每小题4分，共40分，每题均只有一个正确答案）
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
D | B | B | C | B | C | B | A | C | C |
二、填空题（每小题5分，共25分）
11. 5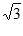
12. 60cm3，116
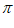cm2 13.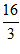 
14. m⊥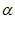
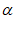，n⊥β，
⊥β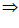
m⊥n或m⊥n，m⊥
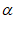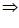
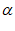，n⊥β
⊥β
15. ①④（注：全部正确得5分，有漏选得3分，有选错或不选得0分）
三、解答题（共5小题，共85分。解答时写出文字说明，演算步骤或证明过程）
16. （本小题14分）
（1）a＝5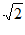
；（II）S△ABC＝15。
17. （本小题14分）
（I）略；
（II）略。
18. （本小题14分）
解：（I）f（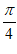
）=-
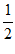
（II）因为f（x）＝（2 cos2 x-1）sin 2x＋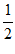
cos 4x＝cos 2x sin 2x＋
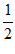cos4x
＝
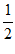（sin4x＋cos4x）＝
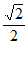sin（4x＋
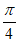），所以f（x）的最小正周期为
，
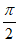（III）当x＝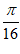
时，最大值为
。
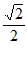19. （本小题14分）
答案：A＝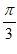
，AD＝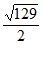
20. （本小题14分）
（I）略；
（Ⅱ）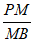
＝
；
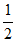（Ⅲ）截面ADNM的面积是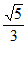
。
21. 答案：
（I）f（A）＝f（B）＝（1，0，1），f（A）×f（B）＝（0，0，0）。
f（A）*f（B）＝（0，0，2）；
（II）由已知可得A1＝（sin（x1-x2），sin（x2-x3），sin（x3-x1）），
B1＝（cos（x1-x2），cos（x2-x3），cos（x3-x1）），进而有
A2＝（sin（x1-2x2＋x3），sin（x2-2x3＋x1），sin（x3-2x1＋x2）），
假设有且只有两个元素为0，则不妨设前两个为0，即有
x1-2x2＋x3＝k1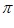
，x2-2x3＋x1＝k2
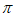，k2，k1∈Z，则有
x3-2x1＋x2＝-[（x1-2x2＋x3）＋（x2-2x3＋x1）］＝–（k1＋k2）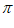
，因此有
sin（x3-2x1＋x2）＝0，所以假设不成立；因此，所证命题成立。
（III）因为A0＝（sinx1，sinx2，…sin xn），B0＝cosx1，cosx2，….cosxn），
A1＝（sin（x1-x2），sin（x2-x3），… sin（xn-x1）），
B1＝（cos（x1-x2），cos（x2 -x3），… cos（xn-x1）），
由已知可知|xi–x i+1｜≤2|x|，i＝1，2，…n，xn+1＝x1（式1），同理在A2和B2中正弦和余弦函数的角度值绝对值小于等于4|x|，依此类推，则Ak和Bk中正弦和余弦函数的角度值绝对值小于等于2k|x|，因此，An-1中第一个元素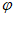
（x）＝sin
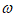x的
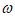满足|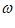
|≤2n-1，因此无论正负，当|
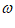|＝2n-1时
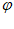（x）＝sin
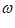x的最小正周期取最小值为
。
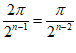此时需满足式1要求，x和-x相间，X＝（x，-x，x，-x…），（-x，x，-x，x……）。