北京市顺义区2020-2021学年下学期初中七年级期末教学质量检测数学试卷
本试卷共三道大题,31道小题,满分100分.考试时间120分钟。
一、选择题(本题共20分,每小题2分)
下列各题均有四个选项,其中只有一个是符合题意的.
1.下列计算正确的是
A.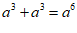 B.
B.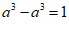
C.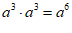 D.
D.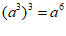
2.下列采用的调查方式中,不合适的是
A.为了了解潮白河的水质,采取抽样调查
B.为了了解顺义区中学生睡眠时间,采取抽样调查
C.为了了解一批灯泡的使用寿命,采取全面调查
D.为了了解某班同学的数学成绩,采取全面调查
3.在电子产品领域当中,芯片的重要性不言而喻,华为的手机芯片——麒麟980是全球首次商用最领先的TSMC 7nm制造工艺,7nm也被称为栅长,简单来说指的是CPU上形成的互补氧化物金属半导体场效应晶体管栅极的宽度为7nm.已知1纳米(nm)=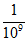 米(m).将7nm用科学记数法表示正确的是
米(m).将7nm用科学记数法表示正确的是
A.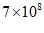 米 B.
米 B.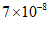 米 C.
米 C.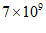 米 D.
米 D.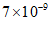 米
米
4.如图,AB∥CD,AD⊥CE于点A,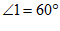 ,则
,则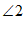 的度数是
的度数是
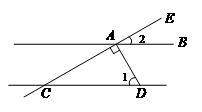
A.30° B.40° C.45° D.60°
5.下列因式分解正确的是
A.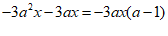 B.
B.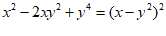
C.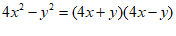 D.
D.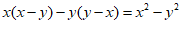
6.在下列方程:①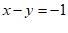 ,②
,②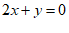 ,③
,③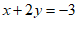 ,④
,④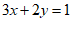 中,任选两个组成二元一次方程组,若
中,任选两个组成二元一次方程组,若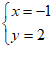 是该方程组的解,则选择的两个方程是
是该方程组的解,则选择的两个方程是
A.①③ B.①④ C.②④ D.②③
7.某中学开展读书活动,为了了解七年级学生自入学以来的读书册数,对从中随机抽取的30名学生的读书册数进行调查,结果如下表所示:
册数/册 | 1 | 2 | 3 | 4 | 5 |
人数/人 | 3 | 7 | 9 | 6 | 5 |
根据统计表中的数据,这30名同学读书册数的众数、中位数分别是
A. 3,9 B. 3,3 C. 2,9 D. 9,3
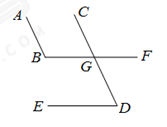
8.如图,∠1=∠A,∠2=∠D,有下列4个结论:①AD∥EF;②AD∥BC,③EF∥BC,④AB∥DC中.则正确结论的个数是
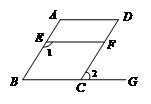
A.4 B.3 C.2 D.1
9.已知关于x,y的二元一次方程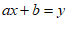 ,当x分别取值时对于y的值如下表所示,则关于x的不等式
,当x分别取值时对于y的值如下表所示,则关于x的不等式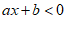 的解集为
的解集为
x | … | -1 | 0 | 1 | 2 | 3 | … |
y | … | 3 | 2 | 1 | 0 | -1 | … |
A.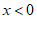 B.
B.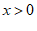 C.
C.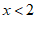 D.
D.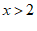
10.已知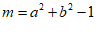 ,
,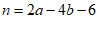 ,则m与n的大小关系是
,则m与n的大小关系是
A.m≥n B.m > n
C.m≤n D.m < n
二、填空题(本题共20分,每小题2分)
11.分解因式: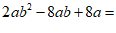
.
12.写出一个解是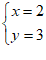 的二元一次方程:
的二元一次方程:
.
13.计算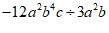 的结果是_____________.
的结果是_____________.
14.如果将一组数据中的每一个数据都减去10,那么对于所得的一组新数据的判断:①众数不变;②中位数改变;③平均数改变.其中正确判断的序号是
.
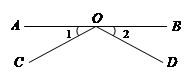
15.如图,点O是直线AB上一点,∠1=∠2,写出图中一对互补的角
,图中共有
对互补的角.
16.数学老师布置10道选择题作为课堂练习,并将全班同学的得分情况绘制成下表,则全班同学这次课堂练习的平均成绩是
分.
成绩/分 | 70 | 80 | 90 | 100 |
人数/人 | 2 | 20 | 10 | 8 |
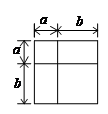
17.利用下图中图形面积关系,写出一个正确的等式:
.
18.当a>b时,关于x的不等式组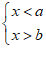 的解集为
的解集为
.
19.已知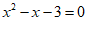 ,则代数式
,则代数式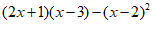 的值为 .
的值为 .
20.甲、乙、丙三人进行羽毛球比赛赛前训练,每局两人进行比赛,第三个人做裁判,每一局都要分出胜负,胜方和原来的裁判进行新一局的比赛,输方转做裁判,依次进行.半天训练结束时,发现甲共当裁判9局,乙、丙分别进行了14局、12局比赛,在这半天的训练中,甲、乙、丙三人共进行了
局比赛,其中最后一局比赛的裁判是
.
三、解答题(共11道小题,共60分)
21.(5分)计算: 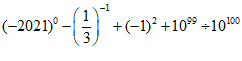 .
.
22.(5分)解方程组: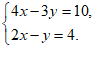
23.(4分)从单项式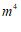 ,
,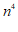 ,
,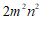 中任选2个,并用”-”号连接成一个多项式,再对其进行因式分解.
中任选2个,并用”-”号连接成一个多项式,再对其进行因式分解.
24.(5分)解不等式组: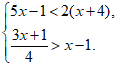
25.(5分)计算: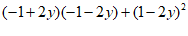 .
.
26.(5分)某中学食堂为1000名学生提供了A、B、C、D四种套餐,为了了解学生对这四种套餐的喜好情况,学校随机抽取200名学生进行”你最喜欢哪一种套餐(必选且只选一种)”问卷调查.根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
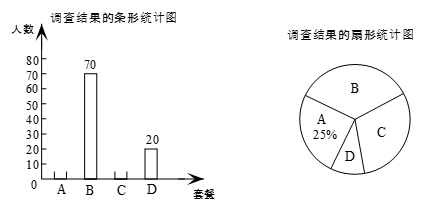
(1)求在抽取的200人中最喜欢A套餐的人数.
(2)求扇形统计图中”C”对应扇形的圆心角度数.
(3)补全条形统计图.
(4)依据本次调查结果,估计全校1000名学生中最喜欢B套餐的人数.
27.(5分)已知:如图,AB∥CD, 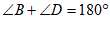 .
.
求证:BF∥ED.
28.(7分)已知x,y满足方程组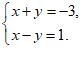 求代数式
求代数式 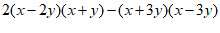 的值.
的值.
29.(7分)为增强中小学生垃圾分类的意识,某校组织了”垃圾分类”知识竞赛,对表现优异的班级进行奖励,学校购买了若干个篮球和排球,购买10个篮球和8个排球共需1 640元;购买20个篮球和10个排球共需2 800元.
(1)求购买1个篮球和1个排球各需多少元?
(2)若学校购买篮球和排球共30个,且支出不超过2 600元,则最多能够购买多少个篮球?
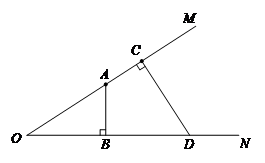
30.(6分)如图,点A、C在∠MON的一边OM上,AB⊥OM于点B,CD⊥OM交射线ON于点D.按要求画图并猜想证明:
(1)过点C画ON的垂线段CE,垂足为点E;
(2)过点E画EF∥OC,交CD于点F.
请你猜想∠OAB与∠CEF的数量关系,并证明你的结论.
31.(6分)现定义运算,对于任意有理数a,b,都有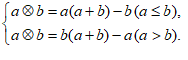
如: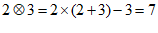 ,
,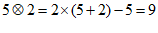 .
.
(1)若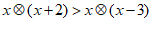 ,求x的取值范围;
,求x的取值范围;
(2)有理数a,b在数轴上的位置如下图所示,计算: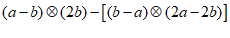 .
.

【试题答案】
一、选择题(本题共20分,每小题2分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | C | C | D | A | B | C | B | B | D | A |
二、填空题(本题共20分,每小题2分)
11.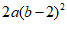 ; 12.
; 12.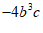 ; 13.略; 14.②③;
; 13.略; 14.②③;
15.如:∠1与∠BOC互补, 4; 16.86; 17.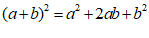 ;
;
18.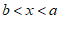 ; 19.
; 19.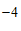 ; 20. 17 , 甲 .
; 20. 17 , 甲 .
三、解答题(本题共60分)
21.解: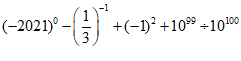
=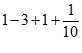 …………………………………………………… 4分
…………………………………………………… 4分
=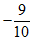 …………………………………………………………………… 5分
…………………………………………………………………… 5分
 22.解:
22.解: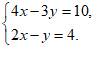
②×2,得 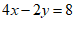 ③ …………………………………… 1分
③ …………………………………… 1分
③-①,得 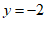 ……………………………………………… 3分
……………………………………………… 3分
把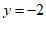 代入②,得
代入②,得 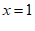 ………………………………………… 4分
………………………………………… 4分
∴原方程组的解是 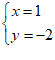 ………………………………………… 5分
………………………………………… 5分
23.解:如: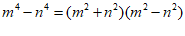 …………………………………… 2分
…………………………………… 2分
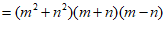 …………………………………… 4分
…………………………………… 4分
 24.解:
24.解: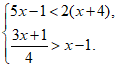
解不等式①,得 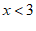 …………………………………………… 2分
…………………………………………… 2分
解不等式②,得 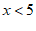 …………………………………………… 4分
…………………………………………… 4分
∴原不等式组的解集为 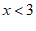 . …………………………………… 5分
. …………………………………… 5分
25.解: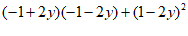
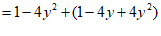 ……………………………………………… 2分
……………………………………………… 2分
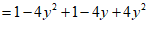 ……………………………………………… 3分
……………………………………………… 3分
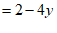 ……………………………………………………………… 5分
……………………………………………………………… 5分
26.解:(1)200×25%=50(人),
在抽取的200人中最喜欢A套餐的有50人. ………………… 1分
(2)200-50-70-20=60,
60÷200×360°=108°. ………………………………………… 2分
(3)补全条形统计图如下:
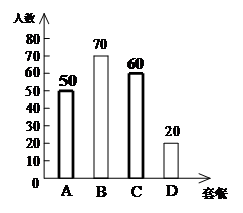
………………………… 4分
(4)60÷200×1000 =300(人),
估计全校1000名学生中最喜欢C套餐的有300人. ………… 5分
27.证明:∵AB∥CD(已知),
∴ ∠B+∠CGB= 180°(两直线平行,同旁内角互补). ……… 2分
∵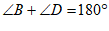 (已知),
(已知),
∴∠CGB =∠D(同角的补角相等). …………………………… 4分
∴ BF∥ED(同位角相等,两直线平行).……………………… 5分
28.解:由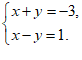
得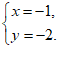 …………………………………………………………… 3分
…………………………………………………………… 3分
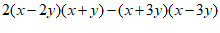 =
=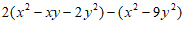
=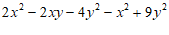
=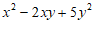 ………………………………………………………… 6分
………………………………………………………… 6分
把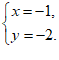 代入上式,得
代入上式,得
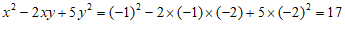 ………… 7分
………… 7分
29.解:(1)设购买1个篮球需要x元,购买1个排球需要y元,根据题意,得
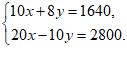 ……………………………………………… 2分
……………………………………………… 2分
解这个方程组,得 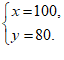 …………………………………… 4分
…………………………………… 4分
答:购买1个篮球、1个排球各需要100元、80元. ……………… 5分
(2)设能购买m个篮球,根据题意,得
100m+80(30-m)≤2600.
解这个不等式,得 m≤10.
答:最多能购买10个篮球. ……………………………………… 7分
30.解:按要求画图如下图:
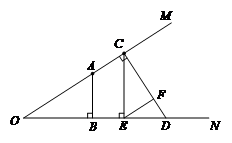
………………………………… 2分
∠OAB与∠CEF的数量关系是:∠OAB = ∠CEF.…………………… 3分
证明:∵ AB⊥ON, CE⊥ON(已知),
∴ ∠OBA=∠OEC=90°(垂直定义).
∴ AB∥CE(同位角相等,两条直线平行). ………………………… 4分
∴∠OAB =∠OCE(两直线平行,同位角相等).
∵ EF∥OC,
∴ ∠OCE =∠CEF.(两直线平行,内错角相等). ……………… 5分
∴ ∠OAB =∠CEF.(等量代换). ………………………………… 6分
31.解:(1)∵ x < x+2,x > x-3,
∴ 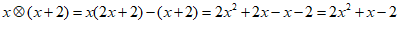 ,
,
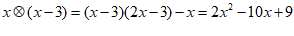 .
.
∵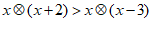 ,
,
∴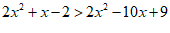 .
.
∴ 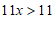 .
.
∴ 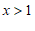 .
.
x的取值范围是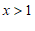 . ……………………………………… 3分
. ……………………………………… 3分
(2)∵a-b<0,2b>0,b-a>0,2a-2b<0,
∴a-b<2b,b-a>2a-2b.
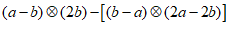
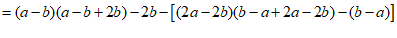
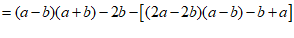
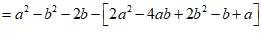
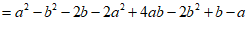
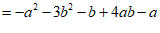 ……………………………………… 6分
……………………………………… 6分
