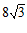北京市门头沟区2020—2021学年下学期初中八年级期末调研数学试卷
本试卷共三道大题,28道小题,满分100分,考试时间120分钟。
一、选择题(本题共16分,每小题2分)
第1-8题均有四个选项,符合题意的选项只有一个.
1.如果点P的坐标是(3,1),那么点P在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.篆书是我国古代书体之一.下列篆体字”美”、”丽”、”北”、”京”中,不是轴对称图形的是
|
|
|
|
A | B | C | D |
3.如果一个多边形的内角和为540°,那么这个多边形的边数是
A.6 B.5 C.4 D.3
4.如果函数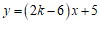 是关于x的一次函数,且y随x增大而增大,那么k取值范围是
是关于x的一次函数,且y随x增大而增大,那么k取值范围是
A. k≠0 B.k<3 C.k≠3 D.k>3
5.将方程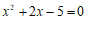 配方后,原方程变形为
配方后,原方程变形为
A.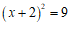 B.
B.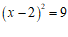 C.
C.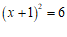 D.
D. 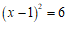
6.下列命题正确的是
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线相等的四边形是矩形 C.有一组邻边相等的四边形是菱形
D.有一组邻边相等且有一个角是直角的平行四边形是正方形
7.某地为发展教育事业,加强了对教育经费的投入,2020年投入4 000万元,预计2022年投入6 000万元,设教育经费的年平均增长率为x,下面所列方程正确的是
A.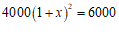 B.
B.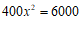
C.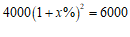 D.
D.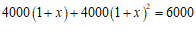
8.某公司新产品上市30天全部售完.图1表示产品的市场日销售量与上市时间之间的关系,图2表示单件产品的销售利润与上市时间之间的关系,下列四个结论中错误的是
A.第30天该产品市场日销售量最大
B.第20天至30天该产品单件产品销售利润最大
C.第20天该产品日销售总利润最大
D.第20天至30天该产品日销售总利润逐日增多
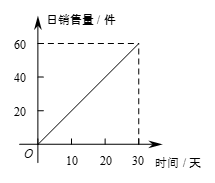
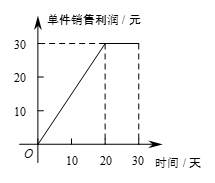
图1 图2
二、填空题(本题共16分,每小题2分)
9.一元二次方程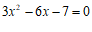 的二次项系数是
的二次项系数是
,常数项是
.
10.在函数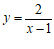 中,自变量x的取值范围是
中,自变量x的取值范围是
.
11.点P(2,1)关于x轴对称点的坐标为
.
12.写出一个图象经过点(1,1)的一次函数的表达式
.
13.在菱形ABCD中,对角线AC与BD交于点O,如果∠ABC =
60°,AC =
4,那么这个菱形的面积是
.
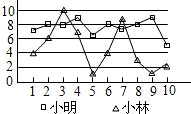
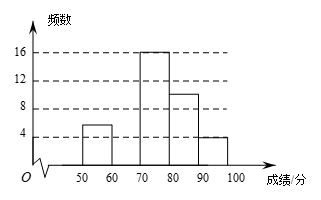
14.有两名学员小林和小明练习射击,第一轮10枪打完后两人打靶的环数如图所示,如果通常新手的成绩都不太稳定,那么根据图中所给的信息,估计小林和小明两人中新手是
(填”小林”或”小明”).
15.写出一个一元二次方程,使其两个根中有一个根为2,此方程为
.
16.在平面直角坐标系xOy中,A(0,1),B(1,1),下面有四种说法:
① 一次函数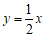 的图象与线段AB有公共点;
的图象与线段AB有公共点;
② 当0≤b≤1时,一次函数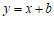 的图象与线段AB有公共点;
的图象与线段AB有公共点;
③ 当k<2,k≠0时,一次函数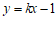 的图象与线段AB有公共点;
的图象与线段AB有公共点;
④ 当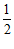 ≤k≤1时,一次函数
≤k≤1时,一次函数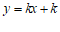 的图象与线段AB有公共点.
的图象与线段AB有公共点.
上述说法中正确的是
(填序号).
三、解答题(本题共68分,第17~21题每小题5分,第22~24题每小题6分,第25题5分,第26题6分,第27~28题每小题7分)
解答应写出文字说明、证明过程或演算步骤.
17.解方程: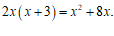
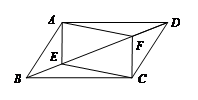
18.已知:如图,E、F是平行四边形ABCD对角线BD上的两点,且BE = DF.
求证:AE = CF.
19.阅读材料,并回答问题:
小明在学习一元二次方程时,解方程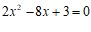 的过程如下:
的过程如下:
解: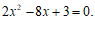
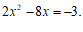 ①
①
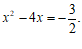 ②
②
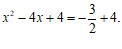 ③
③
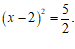 ④
④
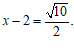 ⑤
⑤
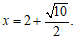 ⑥
⑥
问题:(1)上述过程中,从
步开始出现了错误(填序号);
(2)发生错误的原因是:
;
(3)在下面的空白处,写出正确的解答过程.
20.已知:如图,在□ABCD中,过点D作DE⊥AB于E,点F在边CD上,DF = BE,连接AF和BF.
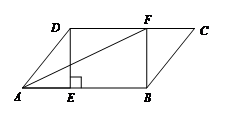
(1)求证:四边形BFDE是矩形;
(2)如果AF平分∠DAB,CF = 3,BF = 4,求DF的长.
21.已知:如图1,线段a,线段b.
求作:菱形ABCD,使其两条对角线的长分别等于线段a,b的长.
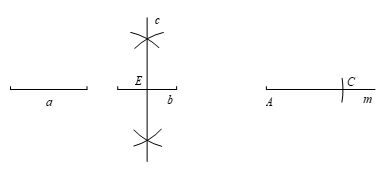
图1 图2
作法:① 如图1,作线段b的垂直平分线c,交线段b于点E;
② 如图2,作射线m,在m上截取线段AC = a;
③ 作线段AC的垂直平分线GF交线段AC于点O;
④ 以点O为圆心,线段b的一半为半径作弧,交直线GF于点B,D;
⑤ 连接AB,BC,CD,DA.
∴ 四边形ABCD就是所求作的菱形.
问题:(1)使用直尺和圆规,依作法补全图2(保留作图痕迹);
(2)完成下面的证明.
证明:∵ OA = OC ,OB = OD,
∴ 四边形ABCD是
.
∵ AC⊥BD,
∴ 四边形ABCD是菱形.(
)(填推理的依据).
22. 如图,将矩形纸片ABCD沿对角线AC折叠,点D落在点F处,AF与BC相交于点E.
如图,将矩形纸片ABCD沿对角线AC折叠,点D落在点F处,AF与BC相交于点E.
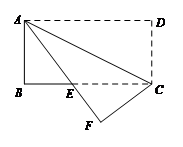
(1)求证:△ABE ≌ △CFE;
(2)如果AB = 4,AD = 8,求AE的长.
23.已知关于x的一元二次方程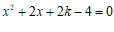 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围;
(2)如果k为正整数,且该方程的根都是整数,求k的值.
24.在平面直角坐标系xOy中,一次函数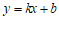 (
(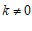 )的图象由函数
)的图象由函数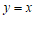 的图象平移得到,且经过点(1,2).
的图象平移得到,且经过点(1,2).
(1)求这个一次函数的表达式;
(2)当x>1时,对于x的每一个值,函数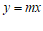 (
(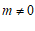 )的值大于
)的值大于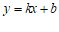 的值,直接写出m的取值范围.
的值,直接写出m的取值范围.
25.为了弘扬中华传统文化,了解学生的整体阅读能力,某校组织全校学生进行了一次阅读理解测试.从中随机抽取了八年级(1)班和八年级(2)班各25人的成绩(单位:分)进行了统计分析.
a.收集数据
(1)班 | 77 | 79 | 80 | 80 | 85 | 86 | 86 | 87 | 88 | 89 | 89 | 90 | 91 |
91 | 91 | 91 | 91 | 92 | 93 | 95 | 95 | 96 | 97 | 98 | 98 | ||
(2)班 | 69 | 79 | 79 | 79 | 86 | 87 | 87 | 89 | 89 | 90 | 90 | 90 | 90 |
90 | 91 | 92 | 92 | 92 | 94 | 95 | 96 | 96 | 97 | 98 | 98 |
b.整理和描述数据
成绩x/分数 | (1)班 | (2)班 | ||
频数 | 频率 | 频数 | 频率 | |
60≤x<70 | 0 | 0 | 1 | 0.04 |
70≤x<80 | 2 | 0.08 | 3 | 0.12 |
80≤x<90 | 9 | a | 5 | 0.20 |
90≤x≤100 | 14 | 16 | 0.64 | |
注:成绩90分及以上为优秀,80~89分为合格,80分以下为不合格.
c.分析数据
两组样本数据的平均数、中位数、众数如下表所示:
班级 | 平均数 | 众数 | 中位数 |
(1)班 | 89.4 | b | 91 |
(2)班 | 89.4 | 90 | c |
根据以上信息,回答下列问题:
(1)表中a =
,b =
,c =
;
(2)在抽取的两班中,测试成绩比较整齐的是
班(填”1″或”2″);
(3)根据调查情况,可以推断
班本次测试成绩较好,理由为
.
26.在平面直角坐标系xOy中,直线l1:y = kx + b经过A(4,1)和B(7,2)两点.
(1)求直线l1的表达式;
(2)如果横、纵坐标都是整数的点叫作整点.直线l2和直线l1关于x轴对称,过点C(m,0)作垂直于x轴的直线l3,l3与l1和l2围的区域为”W”(不包含边界).
① 当m = 3时,求区域”W”内整点的个数;
② 如果区域”W”内恰好有6个整点,直接写出m的取值范围.
27.已知,在正方形ABCD中,连接对角线BD,点E为射线CB上一点,连接AE.F是AE的中点,过点F作FM⊥AE于F,FM交直线BD于M,连接ME、MC.
(1)如图1,当点E在CB边上时
① 依题意补全图1;
② 猜想∠MEC与∠MCE之间的数量关系,并证明.
(2)如图2,当点E在CB边的延长线上时,补全图2,并直接写出∠MEC与∠MCE之间的数量关系.
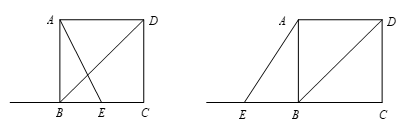
图1 图2
28.在平面直角坐标系xOy中,对于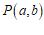 和
和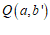 给出如下定义:
给出如下定义:
如果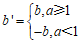 ,那么点Q就是点P的关联点.
,那么点Q就是点P的关联点.
例如,点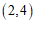 的关联点是
的关联点是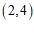 ,点
,点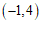 的关联点是
的关联点是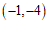 .
.
(1)点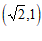 的关联点是
的关联点是
,点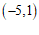 的关联点是
的关联点是
.
(2)如果点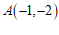 和点
和点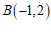 中有一个点是直线
中有一个点是直线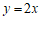 上某一个点的关联点,那么这个点是
上某一个点的关联点,那么这个点是
.
(3)如果点P在直线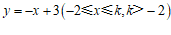 上,其关联点Q的纵坐标
上,其关联点Q的纵坐标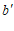 的取值范围是
的取值范围是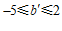 ,求k的取值范围.
,求k的取值范围.
【试题答案】
一、选择题(本题共16分,每小题2分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | A | B | B | D | C | D | A | C |
二、填空题(本题共16分,每小题2分)
题号 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
答案 | 3,-7 | x≠1 | (2,-1) | 略 |
| 小林 | 略 | ②④ |
三、解答题(本题共68分,第17~21题每小题5分,第22~24题每小题6分,第25题5分,第26题6分,第27~28题每小题7分)
17.(本小题满分5分)
解: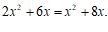 ……………………………………………………………………1分
……………………………………………………………………1分
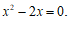 ……………………………………………………………………………2分
……………………………………………………………………………2分
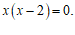 ………………………………………………………………………3分
………………………………………………………………………3分
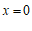 ,
,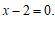 ………………………………………………………………………4分
………………………………………………………………………4分
∴ 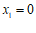 ,
,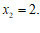 ………………………………………………………………………5分
………………………………………………………………………5分
18.(本小题满分5分)
证明:∵ 四边形ABCD是平行四边形,
∴ AB=CD,AB∥CD. …………………………………………………………………2分
∴ ∠ABE=∠CDF. ……………………………………………………………………3分
又∵ BE=DF.
∴ △ABE≌△CDF. ……………………………………………………………4分
∴ AE=CF. ……………………………………………………………………………5分
19.(本小题满分5分)
解:(1)⑤;………………………………………………………………………………1分
(2)略;……………………………………………………………………………2分
(3)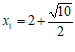 ,
,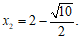 ………………………………………………………5分
………………………………………………………5分
20.(本小题满分5分)
证明:(1)在口ABCD中,AB∥CD,即DF∥BE.
∵ DF=BE,
∴ 四边形BFDE为平行四边形. ………………………………………………1分
∵ DE⊥AB,∴ ∠DEB=90°.
∴ 四边形BFDE为矩形. ………………………………………………………2分
(2)由(1)可得,∠BFC=90°.
在Rt△BFC中,由勾股定理得BC=5. …………………………………………3分
∵四边形ABCD是平行四边形,
∴ AD=BC=5. ……………………………………………………………………4分
∵ AF平分∠DAB,∴ ∠DAF=∠FAB.
又∵ AB∥CD,∴ ∠DFA=∠FAB.
∴ DF=AD=5. ……………………………………………………………………5分
21.(本小题满分5分)
解:(1)作图;……………………………………………………………………………3分
(2)理由.………………………………………………………………………………5分
22.(本小题满分6分)
(1)证明:∵ 矩形ABCD沿对角线AC折叠后,点D落在点F处,
∴ ∠F=∠D=∠B=90°,CD=CF=AB.
又∵∠AEB=∠CEF,
∴ △ABE≌△CFE. ……………………………………………………………3分
(2)解:设AE=x.
∵△ABE≌△CFE,∴CE=AE=x.
∵矩形ABCD,AD=8,
∴BC=AD=8. ………………………………………………………………………4分
∴BE=8-x.
又∵AB=4,
在Rt△ABE中,∠B=90°,
由勾股定理得 (8-x)2+42=x. ……………………………………………………5分
解得x=5.
∴ AE=5. ……………………………………………………………………………6分
23.(本小题满分6分)
解:(1)由题意,得 △=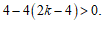
∴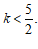 ……………………………………………………………………………2分
……………………………………………………………………………2分
(2)∵ k为正整数,
∴ k=1,2.…………………………………………………………………………3分
当k=1时,方程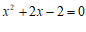 的根
的根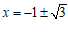 不是整数;……………………4分
不是整数;……………………4分
当k=2时,方程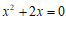 的根
的根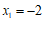 ,
,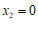 都是整数; …………………5分
都是整数; …………………5分
综上所述,k=2.…………………………………………………………………6分
24.(本小题满分6分)
解:(1)∵ 一次函数y=kx+b的图象由函数y=x的图象平移得到,
∴ k=1. ………………………………………………………………………………2分
又∵ 一次函数y=x+b的图象过点(1,2),
∴ 1+b=2.
∴ b=1. ……………………………………………………………………………4分
∴ 这个一次函数的表达式为y=x+1. ……………………………………………5分
(2)m≥2. ………………………………………………………………………………6分
25.(本小题满分5分)
解:(1)a=0.36,b=91,c=90;……………………………………………………3分
(2)1班;………………………………………………………………………………4分
(3)略. …………………………………………………………………………………5分
26.(本小题满分6分)
解:(1)∵直线l1:y = kx + b经过A(4,1)和B(7,2)两点,
∴ 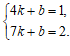 解得
解得 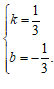
∴直线l1的表达式为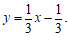 …………………………………………………2分
…………………………………………………2分
(2)① 依题意画出图形
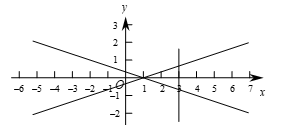
观察图形区域”W”内整点为1个. …………………………………………4分
② 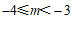 或
或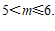 ……………………………………………………6分
……………………………………………………6分
27.(本小题满分7分)
解:(1)① 补全图1;…………………………………………………………………2分
② ∠MEC与∠MCE的数量关系是∠MEC=∠MCE,证明如下:……………3分
如图,连接AM.
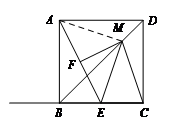
∵ MF是线段AE的垂直平分线,
∴ MA=ME.
又∵ 正方形ABCD,
∴ AD=DC,∠ADM与∠CDM,
又∵ MD=MD,
∴ △ADM≌△CDM,
∴AM=MC.
∴ ME=MC.
∴ ∠MEC=∠MCE. ……………………………………………………………6分
(2)补图略,数量关系为∠MEC=∠MCE . ………………………………………7分
28.(本小题满分7分)
解:(1)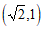 ,
,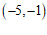 ;……………………………………………………………2分
;……………………………………………………………2分
(2)B;…………………………………………………………………………………4分
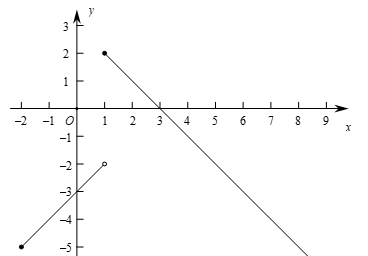
(3)依题意,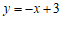 图象上的点P的关联点必在函数
图象上的点P的关联点必在函数
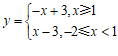 图象上
图象上
∴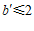 ,即当
,即当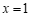 时,
时,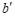 取最大值2.
取最大值2.
当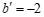 时,
时,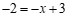 .
.
∴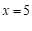 . …………………………………………………………………………5分
. …………………………………………………………………………5分
当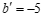 时,
时,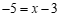 或
或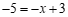 .
.
∴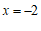 或
或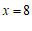 . ………………………………………………………………6分
. ………………………………………………………………6分
∵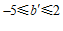 ,
,
由图象可知,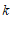 的取值范围是
的取值范围是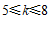 .………………………………………7分
.………………………………………7分
说明:
若考生的解法与给出的解法不同,正确者可参照评分参考相应给分。