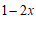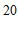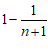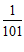北京市门头沟区2020-2021学年下学期初中七年级期末调研数学试卷
本试卷共三道大题,28道小题,满分100分,考试时间120分钟。
一、选择题(本题共16分,每小题2分)
下列各题均有四个选项,其中只有一个是符合题意的.
1.一元一次不等式的解集在数轴上表示如图所示,该不等式的解集为
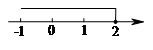
A.x≥2 B.x≤2 C. 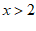 D.
D. 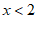
2.北斗卫星导航系统(BDS)是中国自行研制的全球卫星导航系统,未来全球定位精度将优于10米,测速精度将优于0.2米/秒,授时精度将优于0.000 000 02秒,将数字0.000 000 02用科学记数法表示为
A.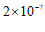 B.
B. 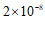 C.
C. 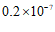 D.
D. 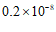
3.下列计算正确的是
A.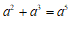
B. 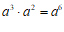 C.
C.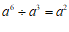 D.
D. 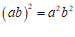
4.下列式子从左到右变形是因式分解的是
A.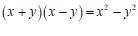 B.
B.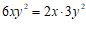
C.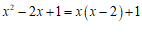 D.
D.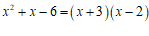
5.下列调查中,适合采用全面调查的是
A.对我国初中生眼睛近视情况的调查
B.对我区市民”五一”出游情况的调查
C.对某班学生的校服尺寸大小的调查
D.对我区市民掌握新冠防疫知识情况的调查
6.《九章算术》是中国传统数学的重要著作,方程术是它的最高成就.其中记载:”今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗.问醇、行酒各得几何?”
译文:今有优质酒1斗的价格是50钱,普通酒1斗的价格是10钱,现在买了两种酒2斗,共付30钱.问优质酒、普通酒各买多少斗?

如果设买优质酒x斗,普通酒y斗,则可列方程组为
A.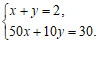 B.
B.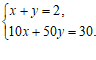
C.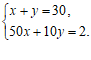 D.
D.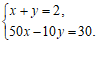
7.如图,直线AB,CD相交于点O,OF⊥OC于O,OE平分∠AOF,如果∠COE=15°,那么∠BOD的度数是
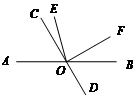
A.75° B.50° C.60° D.70°
8.在新版《北京市生活垃圾管理条例》正式实施一周年之际,某校连续4周开展了”垃圾分类我知道”的知识问答测试活动,并将测试成绩整理,绘制成如下所示的统计图.(注:第1~4周参与测试的学生人数不变)
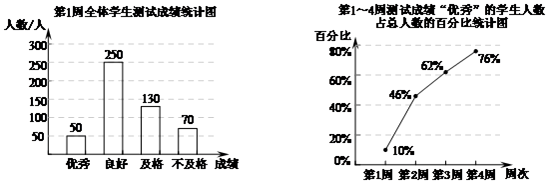
下面有三个推断:
①每周共有500名学生参与测试;
②从第1周到第4周,测试成绩”优秀”的学生人数在总人数中的占比逐周增长,且第2周增长最多;
③第4周测试成绩”优秀”的学生人数达到400人.
其中合理的推断的序号是
A.①② B.①③ C.②③ D.①②③
二、填空题(本题共16分,每小题2分)
9.如果把方程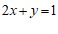 改写成用含x的代数式表示y的形式,那么
改写成用含x的代数式表示y的形式,那么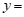 ___________.
___________.
10.如果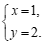 是关于x,y的方程
是关于x,y的方程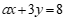 的解,那么
的解,那么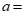 ___________.
___________.
11.如果代数式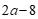 的值是非负数,那么a 的取值范围是___________.
的值是非负数,那么a 的取值范围是___________.
12.如图,将等腰直角三角板放在两条平行线上,如果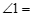 25°,那么
25°,那么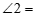 _____°.
_____°.
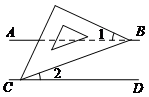
13.用一组a,b,c的值说明命题”如果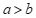 ,那么
,那么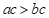 “是假命题,这组值可以是
“是假命题,这组值可以是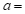 ___________,
___________,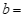 ___________,
___________,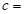 ___________.
___________.
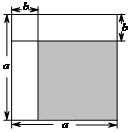
14.下图中的四边形均为长方形或正方形,根据图形的面积关系,写出一个正确的等式:__________________________________.
15.甲,乙,丙三人参与学生会主席选举,共发出1000张选票,得票最高者为当选人,且废票不计入任何一位候选人的得票数内.学校共设有三个投票箱,目前第一、第二投票箱已经统计了所有选票,剩下第三投票箱尚未统计,结果如下表所示:
投票箱 | 候选人 | 废票 | 合计 | ||
甲 | 乙 | 丙 | |||
一 | 123 | 150 | 100 | 12 | 385 |
二 | 135 | 55 | 260 | 15 | 465 |
三 | |||||
那么一定没有机会当选学生会主席的是___________(填”甲”,”乙”或”丙”).
16.符号”f“表示一种运算,它对一些数的运算如下:
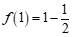 ,
,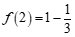 ,
,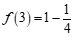 ,
,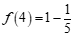 , ……
, ……
利用以上运算的规律,写出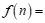 ___________(n为正整数),
___________(n为正整数),
计算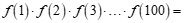 ___________.
___________.
三、解答题(本题共68分,第17-18题,每小题8分,第19题4分,第20-25题,每小题5分,第26-28题,每小题6分)
17.计算:
(1)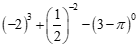 ; (2)
; (2)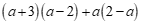 .
.
18.把下列各式分解因式:
(1)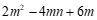 ; (2)
; (2)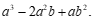
19.解方程组: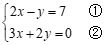 .
.
20.解不等式组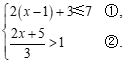 ,并求出这个不等式组的所有的整数解.
,并求出这个不等式组的所有的整数解.
21.如图,∠AOB,点C在边OB上.
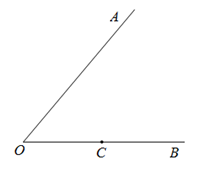
(1)过点C画直线CD⊥OA,垂足为D;
(2)过点C画直线CM∥OA,过点D画直线DN∥OB,直线CM,DN交于点E.
(3)如果∠AOB=50°,那么∠CDE=_________°.
22.先化简,再求值:
已知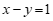 ,求
,求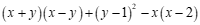 的值.
的值.
23.完成下面的证明:
已知:如图,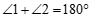 .
.
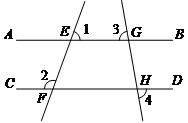
求证: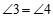 .
.
证明:∵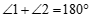 (已知),
(已知),
又∵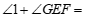 ______°(平角定义),
______°(平角定义),
∴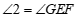 (____________________________________________).
(____________________________________________).
∵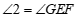 (已证),
(已证),
∴AB∥CD(____________________________________________).
∵AB∥CD(已证),
∴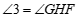 (____________________________________________).
(____________________________________________).
又∵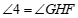 (____________________________________________),
(____________________________________________),
∴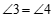 (等量代换).
(等量代换).
24.已知:如图,∠B=∠1,∠A=∠E.
(1)求证:AC∥EF;
(2)如果∠F=60°,求∠ACF的度数.
25.为弘扬”绿水青山门头沟”精神,某中学组织学生开展了”义务植树促环保,我为京西添新绿”社会实践活动.为了了解全校500名学生义务植树情况,小武开展了一次调查研究.
小武从每个班级随机抽取了5名学生进行调查,并将收集的数据(单位:棵)进行整理、描述,绘制成如下两幅不完整的统计图,根据图中提供的信息解答下列问题:
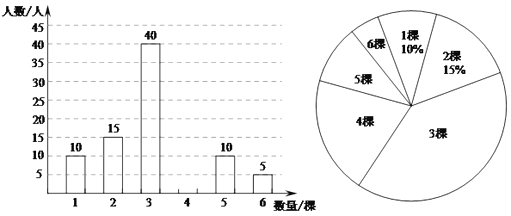
(1)小武一共随机抽取 名学生进行调查;在扇形统计图中,”3棵”所在的扇形的圆心角等于 度;
(2)补全条形统计图;
(3)随机抽取的这部分学生义务植树数量的中位数是 ;
(4)在这次社会实践活动中,学校授予义务植树数量不少于4棵的学生为”植树小能手”的称号,根据调查结果,估计该学校获得”植树小能手”称号的学生有 名.
26.某校组织学生去游乐园参加拓展体验活动,活动中有”空中飞人”和”保卫地球”两个体验项目供同学选择. 如果4名同学选择”空中飞人”,1名同学选择”保卫地球”,购票费用共需210元;如果3名同学选择”空中飞人”,2名同学选择”保卫地球”,购票费用共需220元.
(1)求每张”空中飞人”的票价和每张”保卫地球”的票价各为多少元;
(2)在(1)的条件下,某班有45名同学全部参加体验,老师要求购票总费用不超过2000元,那么最少有多少名同学选择”空中飞人”体验项目?
27.已知,直线AB∥CD,直线EF交AB,CD于点E,F,动点P为平面上一点(点P不在AB,CD,EF上),连接PE,PF .
(1)如图1,当动点P在直线AB,CD之间,且位于直线EF右侧时,
①依题意补全图1;
②猜想∠EPF,∠PEB,∠PFD的数量关系,并证明.
(2)如图2,当动点P在直线AB上方时,直接写出∠EPF,∠PEB,∠PFD的数量关系.
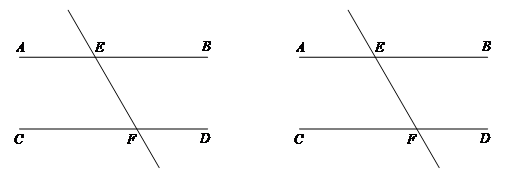
图1 图2
28.对于两个非零实数a,b定义一种新运算,记作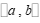 .
.
定义:如果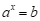 ,那么
,那么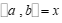 (
(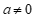 ,
,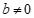 ,x为整数).
,x为整数).
例如:因为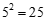 ,所以
,所以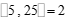 ;因为
;因为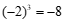 ,所以
,所以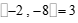 .
.
根据上述运算的定义,回答下列问题:
(1)计算: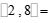 ___________,
___________,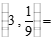 ___________;
___________;
(2)如果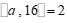 ,那么
,那么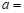 ___________;
___________;
(3)如果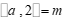 ,
,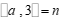 ,那么
,那么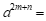 ___________;
___________;
(4)如果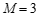 ,
,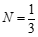 ,那么
,那么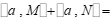 ___________.
___________.
【试题答案】
一、选择题(本题共30分,每小题3分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | B | B | D | D | C | A | C | A |
二、填空题(本题共18分,每小题3分)
题号 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
答案 |
| 2 | a≥4 |
| 略 |
| 乙 |
|
三、解答题(本题共68分,第17-18题,每小题8分,第19题4分,第20-25题,每小题5分,第26-28题,每小题6分)
17.(本小题满分8分)
(1)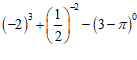 .
.
解:原式=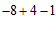 , …………………………………………………………………3分
, …………………………………………………………………3分
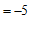 ,………………………………………………………………………………4分
,………………………………………………………………………………4分
(2)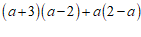 .
.
解:原式=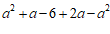 , ………………………………………………2分
, ………………………………………………2分
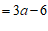 , ……………………………………………………………………………4分
, ……………………………………………………………………………4分
18.(本小题满分8分)
(1)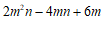 .
.
解:原式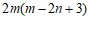 , …………………………………………………………4分
, …………………………………………………………4分
(2)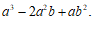 ;
;
解:原式=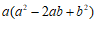 ,………………………………………………………2分
,………………………………………………………2分
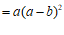 . ………………………………………………………………………4分
. ………………………………………………………………………4分
19.(本小题满分4分)
解方程组: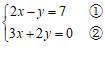 .
.
解:①×2得 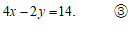 ………………………………………………1分
………………………………………………1分
②+③得 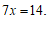
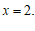 …………………………………………………………………………2分
…………………………………………………………………………2分
把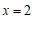 代入①得
代入①得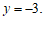 …………………………………………………………………3分
…………………………………………………………………3分
所以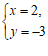 是原方程组的解. …………………………………………………………4分
是原方程组的解. …………………………………………………………4分
20.(本小题满分5分)
解:原不等式组为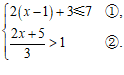
解:解不等式①,得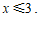 …………………………………………………………1分
…………………………………………………………1分
解不等式②,得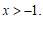 ………………………………………………………………2分
………………………………………………………………2分
∴ 原不等式组的解集为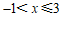 ………………………………………………4分
………………………………………………4分
∴ 原不等式组的所有整数解为0,1,2,3. …………………………………………5分
21.(本小题满分5分)
解:(1)略;……………………………………………………………………………1分
(2)略;…………………………………………………………………………………4分
(3)40.…………………………………………………………………………………5分
22.(本小题满分5分)
解: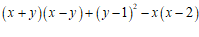
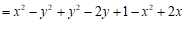 ………………………………………………3分
………………………………………………3分
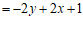 ………………………………………………………………………4分
………………………………………………………………………4分
∵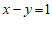 ,
,
∴原式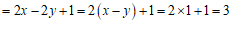 ……………………………………5分
……………………………………5分
23.(本小题满分5分)
解:180 ; ……………………………………………………………………1分
同角的补角相等 ; …………………………………………………………………2分
内错角相等,两直线平行;……………………………………………………………3分
两直线平行,同位角相等;……………………………………………………………4分
对顶角相等.………………………………………………………………………………5分
24.(本小题满分5分)
解:(1)证明:∵∠B=∠1(已知),
∴AB∥DE(同位角相等,两直线平行).………………………………1分
∴∠A=∠AME(两直线平行,内错角相等) .……………………………2分
又∵∠A=∠E(已知),
∴∠E=∠AME(等量代换).……………………………………………3分
∴AC∥EF(内错角相等,两直线平行).………………………………4分
(2)∵AC∥EF(已证),
∴∠ACF+∠F=180°(两直线平行,同旁内角互补) .
∵∠F=60°(已知)
∴∠ACF =120°……………………………………………………………………5分
25.(本小题满分5分)
解:(1)100,144;……………………………………………………………………2分
(2)略 ;…………………………………………………………………………………3分
(3)3; …………………………………………………………………………4分
(4)175. ……………………………………………………………………………5分
26.(本小题满分6分)
解:(1)设每张”空中飞人”的票价x元,每张”保卫地球”的票价y元.………1分
根据题意,得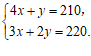 …………………………………………… 3分
…………………………………………… 3分
解得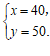 ………………………………………………………… 4分
………………………………………………………… 4分
答:每张”空中飞人”的票价40元,每张”保卫地球”的票价50元.
(2)设m名同学选择”空中飞人”体验项目,那么(45-m)名同学选择”保卫地球”体验项目.
根据题意,得: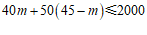 ,…………………………………… 5分
,…………………………………… 5分
解得: m≥25.
答:最少有25名同学选择”空中飞人”体验项目.…………………………6分
27.(本小题满分6分)
解:(1) ①补全图形;………………………………………………………… 1分
② ∠EPF=∠PEB+∠PFD .
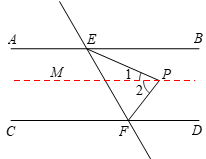
证明:过点P作PM∥AB.
∵AB∥CD,
∴CD ∥PM.………………………………………………………2分
∴ ∠PEB=∠1,∠PFD=∠2;………………………………3分
∵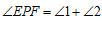 ,
,
∴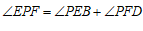 .………………………………………4分
.………………………………………4分
(3)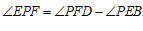 ,
,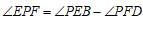 .……………………6分
.……………………6分
28.(本小题满分6分)
解:(1)3,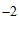 ;……………………………………………………………………2分
;……………………………………………………………………2分
(2)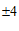 ; ……………………………………………………………………………4分
; ……………………………………………………………………………4分
(3)12; ………………………………………………………………………………5分
(4)0.…………………………………………………………………………………6分
说明:
若考生的解法与给出的解法不同,正确者可参照评分参考相应给分。