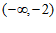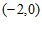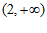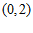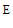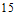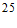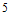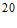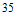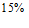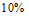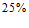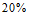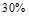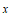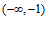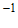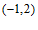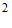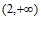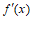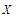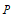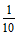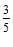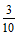北京市西城区2020-2021学年下学期高二年级期末考试数学试卷
本试卷共150分。考试时长120分钟。
第一部分(选择题
共40分)
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 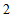 与
与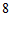 的等差中项是
的等差中项是
A. | B. |
C. | D. |
2. 已知函数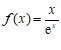 ,则
,则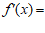
A. | B. |
C. | D. |
3. 在抛物线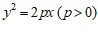 上,若横坐标为
上,若横坐标为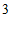 的点到焦点的距离为
的点到焦点的距离为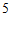 ,则
,则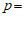
A. | B. |
C. | D. |
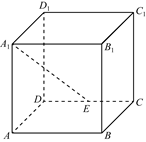
4. 如图,在正方体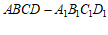 中,
中, 为
为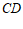 的中点,则直线
的中点,则直线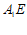 与
与 所成角的余弦值为
所成角的余弦值为
A. 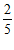 B.
B. 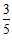 C.
C. 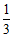 D.
D. 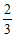
5. 圆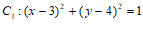 和圆
和圆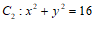 的位置关系为
的位置关系为
A. 内切 | B. 相交 |
C. 外切 | D. 外离 |
6. 设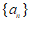 是公比为
是公比为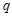 的等比数列,且
的等比数列,且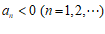 。若
。若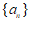 为递增数列,则
为递增数列,则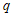 的取值范围是
的取值范围是
A. | B. |
C. | D. |
7. 将一枚质地均匀的硬币连续抛掷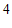 次,记
次,记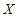 为“正面朝上“出现的次数,则随机变量
为“正面朝上“出现的次数,则随机变量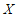 的方差
的方差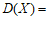
A. | B. |
C. | D. |
8. 在空间直角坐标系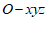 中,已知
中,已知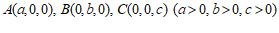 ,且
,且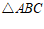 的面积为
的面积为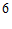 。过
。过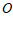 作
作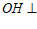 平面
平面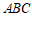 于点
于点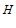 。若三棱锥
。若三棱锥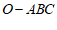 的体积为
的体积为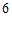 ,则点
,则点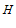 的坐标可以为
的坐标可以为
A. | B. |
C. | D. |
9. 记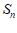 为数列
为数列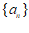 的前
的前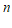 项和。若
项和。若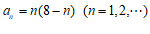 ,则
,则
A. | B. |
C. | D. |
10. 已知函数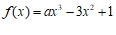 。若
。若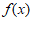 有且只有一个零点
有且只有一个零点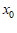 ,且
,且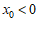 ,则实数
,则实数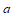 的取值范围是
的取值范围是
A. | B. |
C. | D. |
第二部分(非选择题
共110分)
二、填空题共5小题,每小题5分,共25分。
11. 已知函数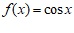 ,则
,则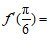 _____。
_____。
12. 已知双曲线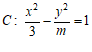 的焦距为
的焦距为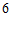 ,则实数
,则实数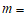 _____;
_____;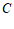 的渐近线方程为_____。
的渐近线方程为_____。
13. 甲、乙两地降雨的概率分别为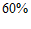 和
和 ,两地同时降雨的概率为
,两地同时降雨的概率为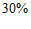 。则在甲地降雨的条件下,乙地也降雨的概率为_____。
。则在甲地降雨的条件下,乙地也降雨的概率为_____。
14. 用铁皮围成一个容积为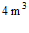 的无盖正四棱柱形水箱,需用铁皮的面积至少为_____
的无盖正四棱柱形水箱,需用铁皮的面积至少为_____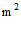 。(注:铁皮厚度不计,接缝处损耗不计)
。(注:铁皮厚度不计,接缝处损耗不计)
15. 已知点列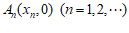 ,其中
,其中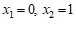 。
。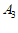 是线段
是线段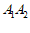 的中点,
的中点,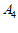 是线段
是线段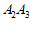 的中点,…,
的中点,…,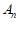 是线段
是线段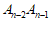 的中点,…。记
的中点,…。记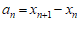 。则
。则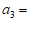 _____;
_____;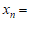 _____。
_____。
三、解答题共6小题,共85分。解答应写出文字说明,演算步骤或证明过程。
16. (本小题13分)
已知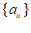 是等比数列,
是等比数列,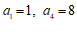 。
。
(Ⅰ)求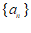 的通项公式;
的通项公式;
(Ⅱ)若等差数列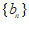 满足
满足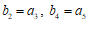 ,求
,求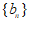 的前
的前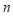 项和
项和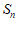 。
。
17. (本小题13分)
已知函数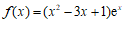 。
。
(Ⅰ)求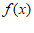 的单调区间;
的单调区间;
(Ⅱ)求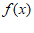 在区间
在区间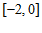 上的最大值和最小值。
上的最大值和最小值。
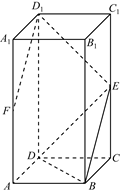
18. (本小题15分)
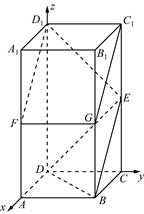
如图,在长方体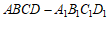 中,底面
中,底面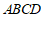 是边长为
是边长为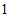 的正方形,
的正方形,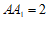 ,
,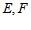 分别为
分别为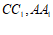 的中点。
的中点。
(Ⅰ)求证: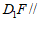 平面
平面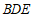 ;
;
(Ⅱ)求直线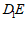 与平面
与平面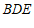 所成角的正弦值;
所成角的正弦值;
(Ⅲ)求直线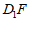 与平面
与平面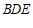 之间的距离。
之间的距离。
19. (本小题14分)
某超市销售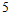 种不同品牌的牙膏,它们的包装规格均相同,销售价格(元/管)和市场份额(指该品牌牙膏的销售量在超市同类产品中所占比重)如下:
种不同品牌的牙膏,它们的包装规格均相同,销售价格(元/管)和市场份额(指该品牌牙膏的销售量在超市同类产品中所占比重)如下:
牙膏品牌 |
|
|
|
|
|
销售价格 |
|
|
|
|
|
市场份额 |
|
|
|
|
|
(Ⅰ)从这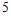 种不同品牌的牙膏中随机抽取
种不同品牌的牙膏中随机抽取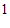 管,估计其销售价格低于
管,估计其销售价格低于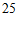 元的概率;
元的概率;
(Ⅱ)依市场份额进行分层抽样,随机抽取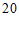 管牙膏进行质检,其中
管牙膏进行质检,其中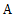 和
和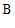 共抽取了
共抽取了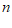 管。
管。
(ⅰ)求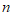 的值;
的值;
(ⅱ)从这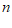 管牙膏中随机抽取
管牙膏中随机抽取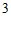 管进行氟含量检测。记
管进行氟含量检测。记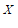 为抽到品牌
为抽到品牌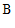 的牙膏数量,求
的牙膏数量,求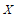 的分布列和数学期望。
的分布列和数学期望。
(Ⅲ)品牌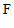 的牙膏下月进入该超市销售,定价
的牙膏下月进入该超市销售,定价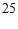 元/管,并占有一定市场份额。原有
元/管,并占有一定市场份额。原有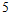 个品牌的牙膏销售价格不变,所占市场份额之比不变。设本月牙膏的平均销售价为每管
个品牌的牙膏销售价格不变,所占市场份额之比不变。设本月牙膏的平均销售价为每管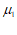 元,下月牙膏的平均销售价为每管
元,下月牙膏的平均销售价为每管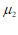 元,比较
元,比较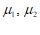 的大小。(只需写出结论)
的大小。(只需写出结论)
20.(本小题15分)
已知椭圆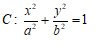 的离心率为
的离心率为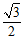 ,且过点
,且过点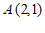 。
。
(Ⅰ)求椭圆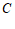 的方程;
的方程;
(Ⅱ)过点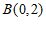 作斜率为
作斜率为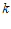 的直线交椭圆
的直线交椭圆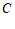 于点
于点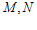 ,直线
,直线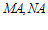 分别交直线
分别交直线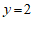 于点
于点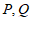 。求证:
。求证: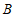 为
为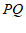 的中点。
的中点。
21. (本小题15分)
已知函数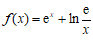 。
。
(Ⅰ)求曲线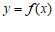 在点
在点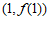 处的切线方程;
处的切线方程;
(Ⅱ)证明: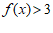 。
。
参考答案
一、选择题(共10小题,每小题4分,共40分)
1. B | 2. C | 3. D | 4. D | 5. C |
6. C | 7. B | 8. B | 9. A | 10. C |
二、填空题(共5小题,每小题5分,共25分)
11. 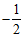 12.
12. 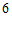
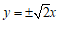
13. 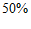 14.
14. 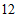
15. 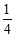
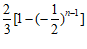
注:(12)、(15)题第一空2分,第二空3分。
三、解答题(共6小题,共85分)
16.(共13分)
解:(Ⅰ)设等比数列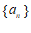 的公比为
的公比为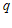 .
.
由题设,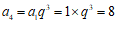 , …………2分
, …………2分
解得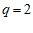 .
.
…………4分
所以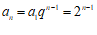 .
.
…………6分
(Ⅱ)设等差数列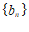 的公差为
的公差为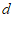 .
.
因为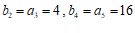 ,
,
所以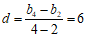 . …………8分
. …………8分
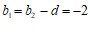 . …………10分
. …………10分
所以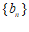 的前
的前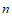 项和
项和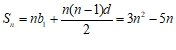 . …………13分
. …………13分
17. (共13分)
解:(Ⅰ)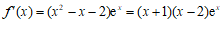 .
.
…………2分
令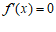 ,得
,得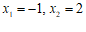 .
.
…………4分
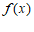 与
与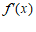 的变化情况如下:
的变化情况如下:
|
|
|
|
|
|
|
|
|
|
|
|
| ↗ | ↘ | ↗ |
所以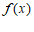 的单调递减区间为
的单调递减区间为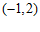 ,单调递增区间为
,单调递增区间为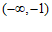 和
和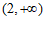 .
.
…………7分
(Ⅱ)由(Ⅰ)知,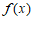 在区间
在区间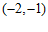 上单调递增,在区间
上单调递增,在区间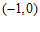 上单调递减.
上单调递减.
所以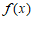 在区间
在区间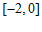 上的最大值为
上的最大值为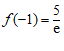 .
.
…………9分
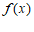 在区间
在区间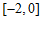 上的最小值为
上的最小值为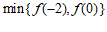 .
.
…………11分
因为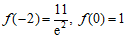 ,且
,且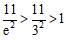 ,
,
所以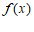 在区间
在区间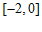 上的最小值为
上的最小值为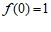 .
.
…………13分
18.(共15分)
解:(Ⅰ)取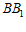 的中点
的中点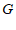 ,连接
,连接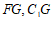 .
.
因为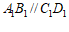 ,且
,且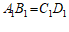 ;
;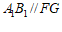 ,且
,且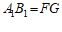 ,
,
所以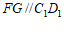 ,且
,且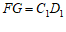 .
.
所以四边形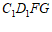 为平行四边形.
为平行四边形.
所以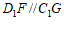 . …………1分
. …………1分
在矩形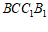 中,因为
中,因为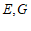 分别为
分别为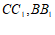 的中点,
的中点,
所以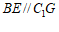 .所以
.所以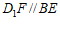 . …………2分
. …………2分
又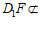 平面
平面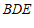 , …………3分
, …………3分
所以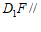 平面
平面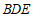 . …………4分
. …………4分
(Ⅱ)如图建立空间直角坐标系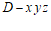 . …………5分
. …………5分
则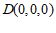 ,
,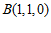 ,
,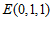 ,
,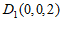 .
.
所以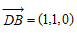 ,
,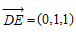 ,
,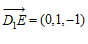 .
.
设平面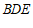 的法向量为
的法向量为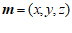 ,则
,则
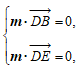 即
即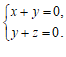 …………7分
…………7分
令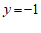 ,则
,则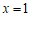 ,
,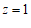 ,于是
,于是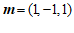 . …………8分
. …………8分
设直线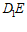 与平面
与平面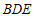 所成角为
所成角为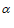 ,则
,则
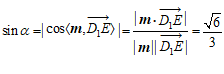 . …………11分
. …………11分
(Ⅲ)由(Ⅰ)知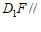 平面
平面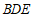 ,
,
所以直线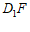 与平面
与平面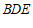 之间的距离为点
之间的距离为点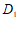 到平面
到平面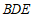 的距离.
的距离.
…………13分
所以直线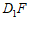 与平面
与平面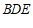 之间的距离为
之间的距离为
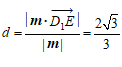 . …………15分
. …………15分
19.(共14分)
解:(Ⅰ)记“从该超市销售的牙膏中随机抽取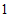 管,其销售价格低于
管,其销售价格低于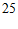 元“为事件
元“为事件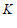 .
.
由题设,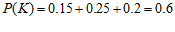 . …………3分
. …………3分
(Ⅱ)(ⅰ)由题设,品牌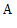 的牙膏抽取了
的牙膏抽取了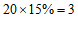 管,
管,
品牌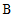 的牙膏抽取了
的牙膏抽取了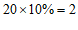 管,
管,
所以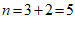 . …………5分
. …………5分
(ⅱ)随机变量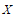 的可能取值为
的可能取值为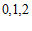 .
.
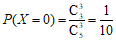 ;
;
…………6分
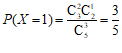 ;
;
…………7分
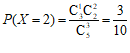 . …………8分
. …………8分
所以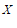 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
…………9分
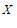 的数学期望为
的数学期望为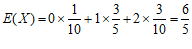 . …………11分
. …………11分
(Ⅲ)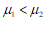 . …………14分
. …………14分
20.(共15分)
解:(Ⅰ)由题设,得
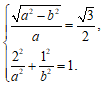 …………2分
…………2分
解得
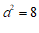 ,
,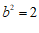 .
.
所以椭圆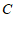 的方程为
的方程为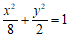 . …………4分
. …………4分
(Ⅱ)由题意,设直线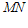 的方程为
的方程为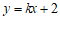 .
.
由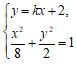 得
得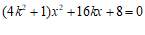 . …………5分
. …………5分
由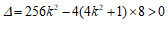 ,得
,得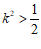 .
.
设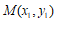 ,
,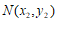 ,则
,则
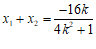 ,
,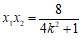 . …………7分
. …………7分
①当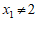 时,直线
时,直线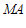 的方程为
的方程为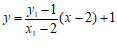 .
.
令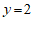 ,得点
,得点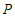 的横坐标
的横坐标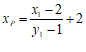 . …………8分
. …………8分
同理可得点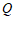 的横坐标
的横坐标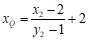 . …………9分
. …………9分
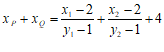
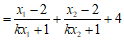 …………10分
…………10分
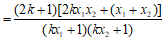 . …………12分
. …………12分
因为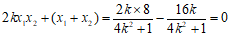 ,所以
,所以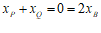 .
.
所以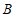 为
为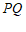 的中点. …………13分
的中点. …………13分
②当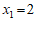 时,
时,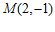 ,
,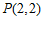 .
.
直线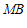 的方程为
的方程为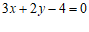 ,可求得
,可求得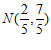 .
.
所以直线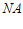 的方程为
的方程为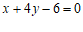 ,从而
,从而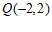 .
.
此时依然有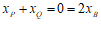 . …………15分
. …………15分
综上,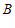 为
为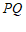 的中点.
的中点.
21.(共15分)
解:(Ⅰ)函数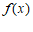 的定义域为
的定义域为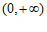 .
.
…………1分
且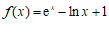 ,
,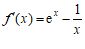 . …………3分
. …………3分
因为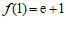 ,
,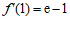 , …………5分
, …………5分
故所求的切线方程为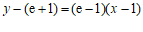 ,即
,即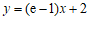 .
.
…………6分
(Ⅱ)由(Ⅰ)可知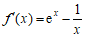 为
为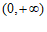 上的增函数. …………7分
上的增函数. …………7分
因为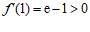 ,
,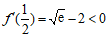 ,
,
所以存在唯一的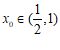 ,使
,使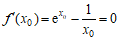 . …………9分
. …………9分
从而有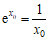 ,
,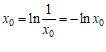 . …………11分
. …………11分
因为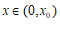 时,
时,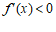 ;
;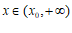 时,
时,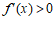 ,
,
所以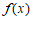 在区间
在区间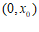 上单调递减,在区间
上单调递减,在区间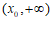 上单调递增.
上单调递增.
…………13分
所以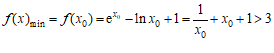 .
.
所以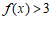 . …………15分
. …………15分

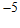
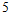
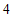
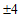
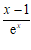
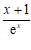
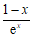
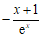
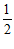
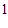
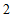
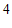
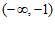
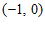
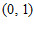
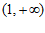
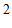
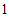
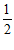
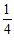
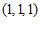
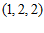
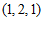
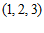
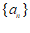
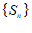 有最大项
有最大项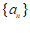
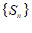 有最小项
有最小项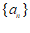
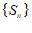 有最大项
有最大项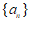
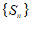 有最小项
有最小项