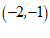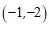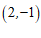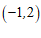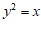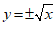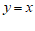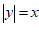北京市石景山区2020-2021学年下学期初中八年级期末考试数学试卷
本试卷共三道大题,28道小题.满分100分,考试时间100分钟。
一、选择题(本题共16分,每小题2分)
下面各题均有四个选项,符合题意的选项只有一个.
1.在平面直角坐标系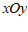 中,点
中,点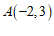 关于原点对称的点的坐标为
关于原点对称的点的坐标为
A. | B. | C. | D. |
2.下列标识中是中心对称图形的是

A. | B. | C. | D. |
3.如果一个多边形的内角和是外角和的2倍,那么这个多边形的边数为
A. | B. | C. | D. |
4.如图,小山为了测量某湖两岸A,B两点间的距离,先在AB外选定一点C,然后测量得到CA,CB的中点D,E,且DE=8m,从而计算出A,B两点间的距离是
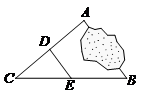
A. | B. | C. | D. |
5.不解方程,判断关于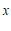 的一元二次方程
的一元二次方程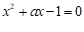 的根的情况为
的根的情况为
A. 有两个不相等的实数根 | B. 有两个相等的实数根 |
C. 只有一个实数根 | D. 没有实数根 |
6.如图是某动物园的示意图,若分别以正东、正北方向为x轴、y轴的正方向建立平面直角坐标系,表示狮虎山的点的坐标为 ,表示熊猫馆的点的坐标为
,表示熊猫馆的点的坐标为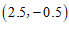 ,则表示百鸟园的点的坐标为
,则表示百鸟园的点的坐标为

A. | B. |
C. | D. |
7.在下列关于变量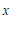 ,
,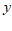 的关系式中,能够表示
的关系式中,能够表示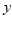 是
是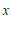 的函数关系的是
的函数关系的是
A. | B. | C. | D. |
8.在□ABCD中,O为AC的中点,点E,M为□ABCD同一边上任意两个不重合的动点(不与端点重合),EO,MO的延长线分别与□ABCD的另一边交于点F,N.
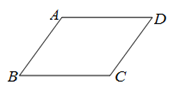
下面四个推断:
① EF=MN
② EN∥MF
③ 若□ABCD是菱形,则至少存在一个四边形ENFM是菱形
④ 对于任意的□ABCD,存在无数个四边形ENFM是矩形
其中,所有正确的有
A. ①③ | B. ②③ | C. ①④ | D. ②④ |
二、填空题(本题共16分,每小题2分)
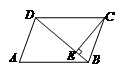
9.函数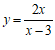 中自变量
中自变量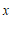 的取值范围是
的取值范围是
.
10.如图Rt△ABC中,∠ACB=90°,点D为AB的中点,若AC=6,BC=8,则CD=
.
11.如图,请给矩形ABCD添加一个条件,使它成为正方形,则此条件可以为
.

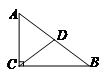
12.如图,在□ABCD中,∠A=70°,DB=DC, CE⊥BD于E,则∠BCE=
.
13.已知一次函数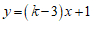 中,
中,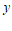 随
随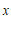 的增大而减小,则
的增大而减小,则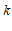 的取值范围是
的取值范围是
.
14.关于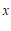 的一元二次方程
的一元二次方程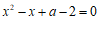 的一个根为1,则
的一个根为1,则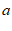 的值为
的值为
.
15.平面直角坐标系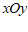 中,点A,B,C,D的位置如图所示,当
中,点A,B,C,D的位置如图所示,当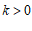 且
且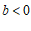 时,A,B,C,D四点中,一定不在一次函数
时,A,B,C,D四点中,一定不在一次函数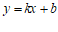 图象上的点为
图象上的点为
.

16.为庆祝中国共产党建党100周年,某高校组织党史知识竞赛.根据小明、小刚5次预赛成绩绘制成下侧的统计图.
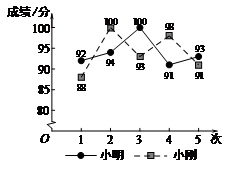
下面有四个推断:
①小明、小刚5次成绩的平均数相同
②与小刚相比,小明5次成绩的极差大
③与小刚相比,小明5次成绩的方差小
④与小明相比,小刚的成绩比较稳定
其中,所有合理推断的序号是
.
三、解答题(本题共68分,第17-21题,每小题5分;第22-24题,每小题6分;第25题5分;第26题6分,27-28题,每小题7分)解答应写出文字说明,演算步骤或证明过程.
17.下面是小阳设计的作矩形的尺规作图过程.
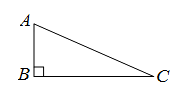
已知:Rt△ABC,∠ABC=90°.
求作:矩形 ABCD.
作法:
①以A为圆心,BC的长为半径画弧,再以C为圆心,
AB的长为半径画弧,两弧交于点D;
②连接DA,DC.
所以四边形ABCD即为所求作的矩形.
根据小阳设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵AD=BC,CD=AB,
∴四边形ABCD是
(
).
∵∠ABC=90°,
∴四边形ABCD是矩形(
).
18.选择适当的方法解方程: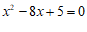 .
.
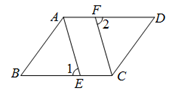
19.已知:如图,E,F分别为□ABCD的边BC,AD上的点,且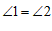 .
.
求证:AE=CF.
20.一次函数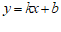 的图象与正比例函数
的图象与正比例函数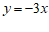 的图象平行,且过点
的图象平行,且过点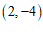 .
.
(1)求一次函数 的表达式;
的表达式;
(2)画出一次函数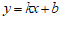 的图象;
的图象;
(3)结合图象解答下列问题:
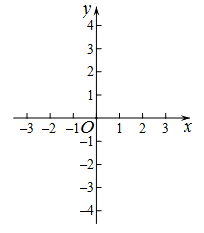
①当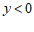 时,
时,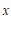 的取值范围是
的取值范围是
;
②当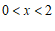 时,
时,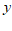 的取值范围是
的取值范围是
.
21.关于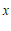 的一元二次方程
的一元二次方程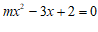 有两个实数根.
有两个实数根.
(1)求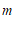 的取值范围;
的取值范围;
(2)若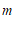 为正整数,求此时方程的根.
为正整数,求此时方程的根.
22.袁隆平是我国研究与发展杂交水稻的开创者,被誉为”杂交水稻之父”,成功选育了世界上第一个实用高产杂交水稻品种.某农业基地现有杂交水稻种植面积20公顷,计划两年后将杂交水稻种植面积增至24.2公顷,求该农业基地杂交水稻种植面积的年平均增长率.
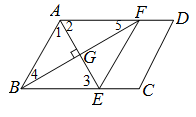
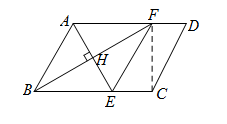
23.如图,在□ABCD中,AE平分∠BAD交BC于点E,过点B作BF⊥AE于点H,交AD于点F,连接EF.
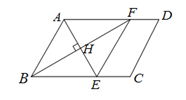
(1)求证:四边形ABEF是菱形;
(2)连接CF,若CE=1,CF=2,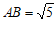 ,求菱形ABEF的面积.
,求菱形ABEF的面积.
24.某校为了解初二年级学生的身高情况,从中随机抽取了40名学生的身高数据,并对数据进行整理、描述和分析. 下面给出了部分信息.
a. 40名学生身高的频数分布表和频数分布直方图如下:
40名学生身高的频数分布表(表1)
身高x(cm) | 频数 | 频率 |
150≤x<155 | 4 | 0.100 |
155≤x<160 | a | 0.300 |
160≤x<165 | 7 | 0.175 |
165≤x<170 | b | m |
170≤x<175 | 8 | 0.200 |
175≤x<180 | 2 | 0.050 |
合计 | 40 | 1.000 |
40名学生身高的频数分布直方图
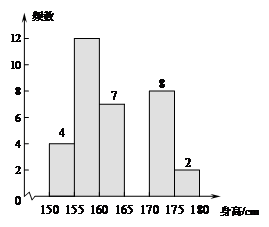
b. 40名学生身高在160≤x<165这一组的数据如下表(表2)所示:
身高(cm) | 160 | 161 | 162 | 163 | 164 |
频数 | 1 | 0 | 1 | 2 | 3 |
根据以上信息,回答下列问题:
(1)表1中a的值为
;
(2)补全该校40名学生身高频数分布直方图;
(3)样本数据的中位数是
;
(4)若该校初二年级共400名学生,估计身高不低于165cm的学生有
人.
25.平面直角坐标系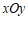 中,直线
中,直线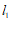 :
: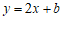 与直线
与直线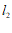 :
: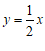 交于点
交于点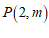 .
.
(1)求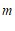 ,
,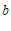 的值;
的值;
(2)直线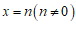 与直线
与直线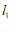 ,
,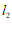 分别交于M,N两点,当MN=3时,若以M,N,P,Q为顶点的四边形是平行四边形,请直接写出点Q的坐标.
分别交于M,N两点,当MN=3时,若以M,N,P,Q为顶点的四边形是平行四边形,请直接写出点Q的坐标.
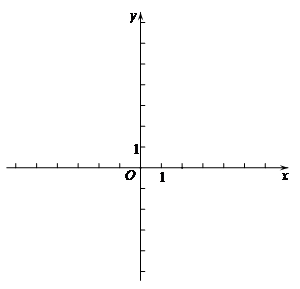
26.小明从学校出发,匀速骑行到相距2400米的图书馆,小明出发的同时,同学小阳以每分钟80米的速度从图书馆沿同一条道路步行回学校,两人离学校的路程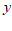 (单位:米)与时间x(单位:分钟)的函数图象如图所示.
(单位:米)与时间x(单位:分钟)的函数图象如图所示.
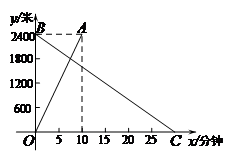
(1)阅读分析题目的文字及图象信息,直接写出能推理得到的三条不同的结论;
(2)若小明在图书馆停留5分钟后沿原路按原速返回,请补全小明离学校的路程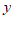 与x的函数图象;
与x的函数图象;
(3)在(2)的条件下,小明从学校出发,经过多长时间在返校途中追上小阳?
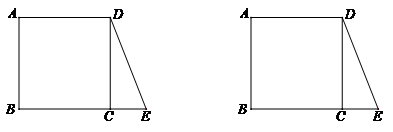
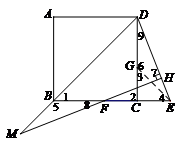
27.已知:如图,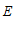 为正方形
为正方形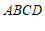 的边BC延长线上一动点,且
的边BC延长线上一动点,且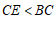 ,连接
,连接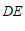 .点F与点E关于直线DC对称,过点F作
.点F与点E关于直线DC对称,过点F作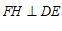 于点H,直线FH与直线DB交于点M.
于点H,直线FH与直线DB交于点M.
(1)依题意补全图1;
(2)若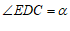 ,请直接写出
,请直接写出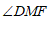 =
=
(用含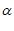 的式子表示);
的式子表示);
(3)用等式表示BM与CF的数量关系,并证明.

28.对于平面直角坐标系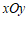 中的线段
中的线段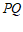 与点R,给出如下定义:若
与点R,给出如下定义:若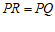 ,则称点R为线段
,则称点R为线段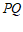 的”
的”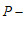 等长点”.
等长点”.
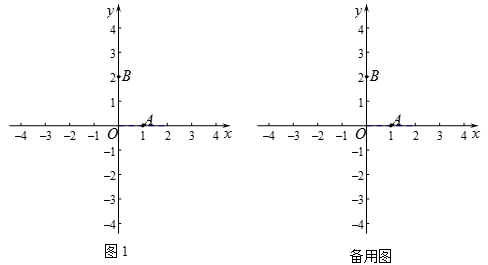
如图1,已知点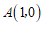 ,
,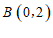 .
.
(1)在点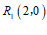 ,
,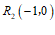 ,
,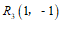 中,线段
中,线段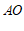 的”
的”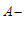 等长点”为
等长点”为
;
(2)若直线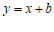 上存在线段
上存在线段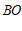 的”
的”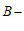 等长点”,求b的取值范围;
等长点”,求b的取值范围;
(3)连接AB,
①若第一象限内的点R是线段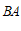 的”
的”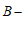 等长点”,且△ABR是直角三角形,则点R的坐标为
等长点”,且△ABR是直角三角形,则点R的坐标为
;
②矩形CDEF中,DE=2,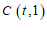 ,
,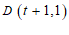 ,若矩形CDEF上存在线段
,若矩形CDEF上存在线段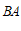 的”
的”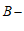 等长点”,直接写出
等长点”,直接写出 的取值范围.
的取值范围.
【试题答案】
阅卷须知:
为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可。若考生的解法与本解法不同,正确者可参照评分参考给分,解答右端所注分数,表示考生正确做到这一步应得的累加分数
一、选择题(本题共16分,每小题2分)
题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答 案 | B | B | C | C | A | A | C | D |
二、填空题(本题共16分,每小题2分)
9.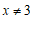 10.
10.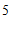 11.答案不唯一,如
11.答案不唯一,如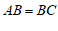 12.
12.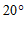 ;
;
13.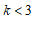 14.
14.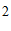 15.D 16.①③
15.D 16.①③
三、解答题(本题共68分,第17-21题,每小题5分;第22-24题,每小题6分;第25题5分;第26题6分,27-28题,每小题7分)解答应写出文字说明,演算步骤或证明过程.
17.解:(1)使用直尺和圆规,补全图形如图所示:
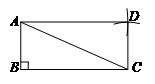
(2)平行四边形;两组对边分别相等的四边形是平行四边形;
有一个角是直角的平行四边形是矩形.
18.解:原方程可化为: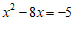
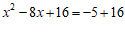 .
.
 .
.
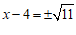 .
.
∴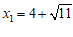 ,
,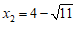 .
.
19.证明:方法一:
∵四边形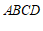 是平行四边形,
是平行四边形,
∴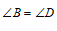 ,
,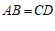 . …………… 2分
. …………… 2分
∵∠1=∠2,
∴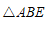 ≌
≌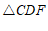 (AAS). ………………4分
(AAS). ………………4分
∴AE=CF. …………………5分
方法二:
∵四边形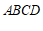 是平行四边形,
是平行四边形,
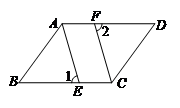
∴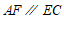 .
.
∴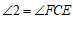 .
.
∵∠1=∠2,
∴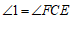 .
.
∴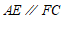 .
.
∴四边形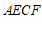 是平行四边形.
是平行四边形.
∴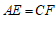 .
.
20.解:(1)根据题意得: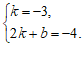
解得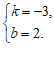
∴一次函数的表达式为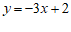 .
.
(2)图象如图所示:
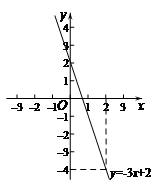
(3)①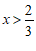 ;
;
②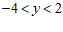 .
.
21.解:(1)∵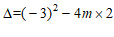
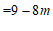 .
.
依题意,得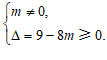
解得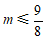 且
且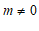 .
.
(2)∵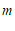 为正整数,
为正整数,
∴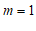 .
.
∴原方程为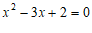 .
.
解得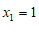 ,
,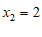 .
.
22.解:该农业基地杂交水稻种植面积的年平均增长率为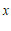 .
.
根据题意,得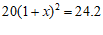 .
.
整理,得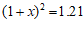 .
.
解得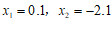 (不合题意,舍去)
(不合题意,舍去)
∴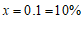 .
.
答:该农业基地杂交水稻种植面积的年平均增长率为10%.
23.(1)证明:
∵四边形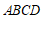 是平行四边形,
是平行四边形,
∴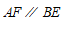 .
.
∴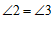 .
.
∵∠1=∠2,
∴∠1=∠3.
∴AB=BE.
∵BF⊥AE,∠1=∠2,
∴∠4=∠5.
∴AB=AF.
∴AF=BE.
∴四边形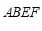 是平行四边形.
是平行四边形.
又∵BF⊥AE,
∴四边形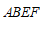 是菱形.
是菱形.
(2)解:连接CF.
∵四边形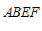 是菱形,
是菱形,
∴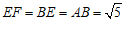 .
.
∵CE=1,CF=2,
∴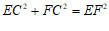 .
.
∴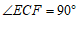 .
.
∴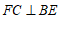 .
.
∴菱形ABEF的面积为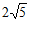 .
.
24.解:(1)12; ………1分
(2)如图所示: ………2分
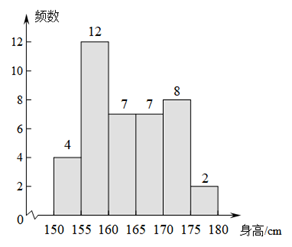
(3)163.5cm; ………4分
(4)170人. ………6分
25.解:(1)∵直线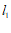 :
: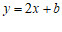 与直线
与直线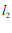 :
: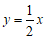 交于点
交于点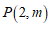 ,
,
∴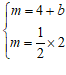
∴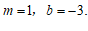
(2)点Q的坐标为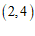 ,
,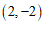 或
或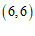 .
.
26.解:(1)答案不唯一,如:
①小明骑车的速度为每分钟240米;
②点C的坐标为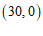 ;
;
③线段OA的函数表达式为 ;
;
④线段BC是小阳离校的路程与时间的函数图象.
(2)补全图象如图所示:
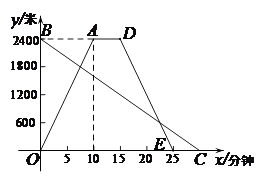
(3)设DE的表达式为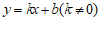 .
.
∵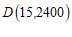 ,
,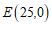 ,
,
∴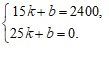 解得
解得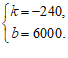
∴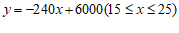 .
.
由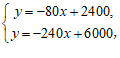 得
得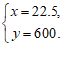
答:小明从学校出发,经过22.5分钟追上小阳.
27.解:(1)补全图形如图所示.
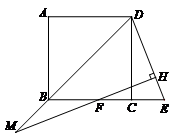
(2)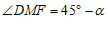 ;
;
(3)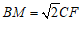 .
.
证明:在CD上取点G,使得CG=CE,连接GE.
∵四边形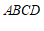 是正方形,
是正方形,
∴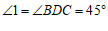 ,
,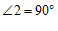 ,BC=DC.
,BC=DC.
∴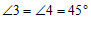 .
.
∴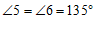 .
.
∴BF=GD.
∵点F与点E关于直线DC对称,
∴CF=CE=CG,且点F在BC上.
∵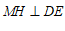 于
于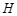 ,
,
∴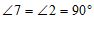 .
.
∴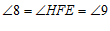 .
.
∴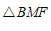 ≌
≌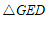 .
.
∴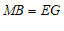 .
.
∵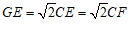 ,
,
∴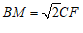 .
.
28.解:(1)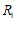 ,
,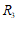 ;
;
(2)如图,过点B作直线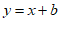 的垂线,垂足为H.
的垂线,垂足为H.
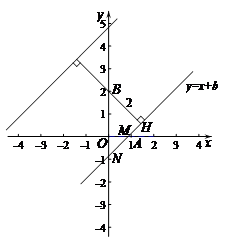
不妨设直线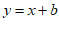 与
与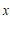 轴交于点M,与
轴交于点M,与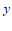 轴交于点N.
轴交于点N.
则易得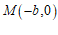 ,
,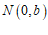 .
.
∴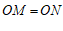 .
.
∴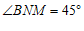 .
.
当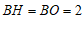 时,
时,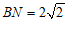
i) 若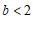 ,则
,则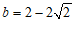 .
.
ii)若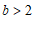 ,则
,则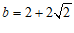 .
.
结合函数图象,可得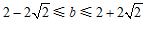 .
.
(3)① 点R的坐标为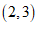 ;
;
② 当线段EF在CD上方时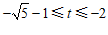 或
或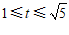 ;
;
当线段EF在CD下方时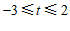 .
.
综上所述: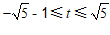

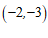
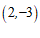
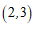
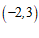
 m
m m
m m
m m
m