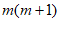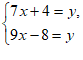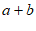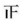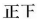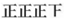北京市昌平区2020-2021学年下学期初中七年级期末质量抽测数学试卷
本试卷共100分。考试时长120分钟。
一、选择题(共8道小题,每小题2分,共16分)第1-8题均有四个选项,符合题意的选项只有一个。
1. 已知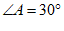 ,那么
,那么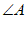 的余角等于(
的余角等于(
)
A. 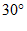 B.
B. 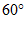 C.
C. 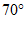 D.
D. 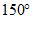
2. 叶绿体是绿色植物进行光合作用的场所,叶绿体DNA最早发现于衣藻叶绿体,长约0.00005米.其中,0.00005用科学记数法表示为(
)
A. 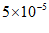 B.
B. 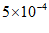 C.
C. 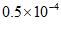 D.
D. 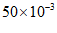
3. 下列计算正确的是(
)
A. 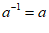 B.
B. 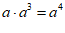 C.
C. 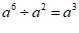 D.
D. 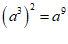
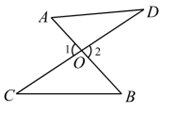
4. 如图,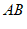 与
与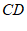 相交于点
相交于点 ,则下列结论正确的是(
,则下列结论正确的是(
)
A. 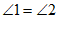 B.
B. 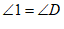 C.
C. 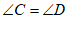 D.
D. 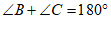
5. 如果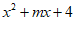 是一个完全平方式,则
是一个完全平方式,则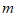 等于(
等于(
)
A. 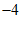 B. 2 C. 4 D.
B. 2 C. 4 D. 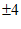
6. 有下列变形:①由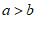 得
得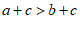 ;②由
;②由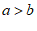 得
得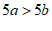 ;③由
;③由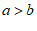 得
得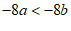 ;④由
;④由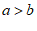 得
得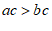 ,其中变形一定正确且使用了“不等式两边都乘(或除以)同一个正数,不等号的方向不变“这一不等式基本性质的是
,其中变形一定正确且使用了“不等式两边都乘(或除以)同一个正数,不等号的方向不变“这一不等式基本性质的是
A. ① B. ② C. ③ D. ④
7. 已知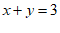 ,如果
,如果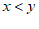 且
且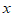 ,
,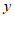 是正整数,那么不等式
是正整数,那么不等式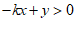 中
中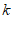 的取值范围是(
的取值范围是(
)
A. 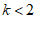 B.
B. 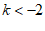 C.
C. 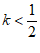 D.
D. 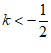
8. 在某学校庆祝建党“100周年“的活动上,宇阳同学用围棋棋子按照某种规律摆成如图所示的“100”字样.按照这种规律,第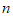 个“100”字样的棋子个数是(
个“100”字样的棋子个数是(
)

A. 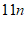 B.
B. 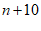 C.
C. 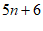 D.
D. 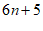
二、填空题(共8道小题,每小题2分,共16分)
9. 分解因式: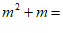 ________。
________。
10. 如果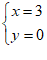 是关于
是关于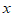 ,
,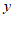 的二元一次方程
的二元一次方程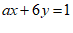 的解,那么
的解,那么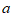 的值是________。
的值是________。
11. 昌平区五月份某一周每天的最高气温统计如下表:
最高气温(℃) | 22 | 24 | 25 | 27 |
天数 | 2 | 3 | 1 | 1 |
则这组数据的平均数是______℃,众数是_____℃.
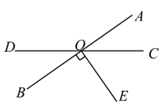
12. 如图所示,直线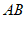 ,
,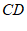 相交于点
相交于点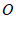 ,
,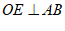 于点
于点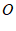 ,如果
,如果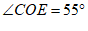 ,那么
,那么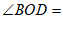 _____
_____ .
.
13. 我国古代数学名著《算法统宗》中有这样一个问题:隔墙听得客分银,不知人数不知银,七两分之多四两,九两分之少半斤。问:人数多少?银子几何?意思是:有若干客人分银若干两,如果每人分7两,还多4两;如果每人分9两,还差8两(题中斤、两为旧制,1斤=16两)。问:有多少位客人?多少两银子?设有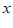 位客人,
位客人,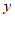 两银子,根据题意,可列方程组为______。
两银子,根据题意,可列方程组为______。
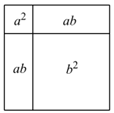
14. 把面积为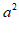 ,
,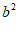 的小正方形和面积为
的小正方形和面积为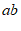 的两个长方形拼成如图所示的大正方形。那么,大正方形的边长为_____.(
的两个长方形拼成如图所示的大正方形。那么,大正方形的边长为_____.(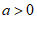 ,
,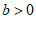 )
)
15 .已知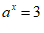 ,
,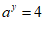 ,则
,则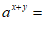 _____.
_____.
16. “体育节“中,初一年级四个班进行了足球单循环比赛,每两班赛一场,胜一场得3分,平一场得1分,负一场得0分.比赛结束后,一班、二班、三班、四班分别获得第一、二、三、四名,各班的总得分恰好是四个连续奇数,那么与二班踢平的班是_____.
三、解答题(本题共12道小题,第17-22题,每小题5分,第23-26题,每小题6分,第27、28题,每小题7分,共68分)
17. 分解因式: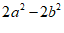 .
.
18. 计算: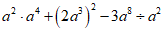 .
.
19. 解不等式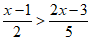 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
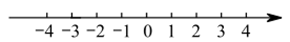
20. 解方程组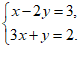
21. 解不等式组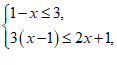 并写出整数解的中位数。
并写出整数解的中位数。
22. 先化简,再求值: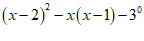 ,其中
,其中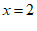 。
。
23. 某集团校对本集团的四个校区的初一学生,围绕着“你最喜欢的居家健身项目是什么(只选一项)“的问题进行了随机抽样调查.过程如下:
收集数据
A. 平板支撑 B. 蹲起 C. 仰卧起坐 D. 开合跳 E.其他
经过调查得到的一组数据如下:
D C C A D A B A D B
B E D D E D B C C E
E C B D E E D D E D
B B C C D C E D D A
B D D C D D E D C E
整理数据
抽样调查50名初一学生最喜欢的居家健身项目人数统计表
活动项目 | 划记 | 频数 |
A.平板支撑 |
| 4 |
B.蹲起 | ||
C.仰卧起坐 | 正正 | 10 |
D.开合跳 | ||
E.其他 | 正正 | 10 |
总计 | 50 |
描述数据
各校区初一学生人数占集团初一学生总人数的百分比
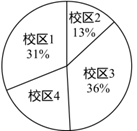
根据以上信息回答下列问题:
(1)补全统计表;
(2)求本次抽样调查中,最喜欢开合跳项目的人数占被调查总人数的百分比;
(3)若校区4共有160名初一学生,请你估计该集团初一学生中,最喜欢蹲起项目的人数约为多少人?
24.(1)阅读以下内容:
已知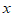 ,
,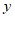 满足
满足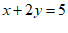 ,且
,且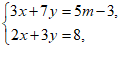 求
求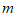 的值。
的值。
三位同学分别提出了以下三种不同的解题思路:
甲同学:先解关于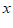 ,
,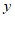 的方程组
的方程组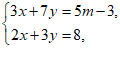 再求
再求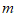 的值.
的值.
乙同学:先将方程组中的两个方程相加,再求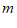 的值.
的值.
丙同学:先解方程组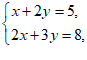 ,再求
,再求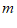 的值.
的值.
(2)你最欣赏(1)中的哪种思路?先根据你所选的思路解答此题,再简要说明你选择这种思路的理由.
请先选择思路,再解答题目。
我选择_______同学的思路(填“甲“或“乙“或“丙“). |
25. 用纸片拼图时,我们发现利用图1中的三种纸片(边长分别为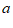 ,
,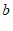 的正方形和长为
的正方形和长为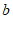 宽为
宽为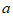 的长方形)各若干,可以拼出一些长方形来解释某些等式,比如图2可以解释为:
的长方形)各若干,可以拼出一些长方形来解释某些等式,比如图2可以解释为: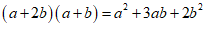 .
.
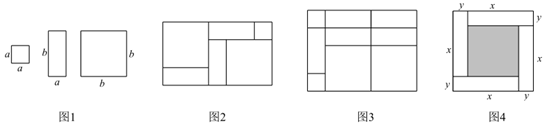
(1)图3可以解释为等式:_______;
(2)要拼出一个两边长为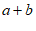 ,
,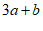 的长方形,先回答需要以下三种纸片各多少块,再用画图或整式乘法验证你的结论;
的长方形,先回答需要以下三种纸片各多少块,再用画图或整式乘法验证你的结论;
 _____块,
_____块, _____块,
_____块,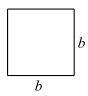 _____块
_____块
(3)如图4,大正方形的边长为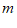 ,小正方形的边长为
,小正方形的边长为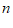 ,若用
,若用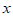 ,
,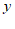 (
(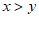 )表示四个相同小长方形的两边长,以下关系式正确的是_____(填序号).
)表示四个相同小长方形的两边长,以下关系式正确的是_____(填序号).
①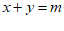 ;②
;②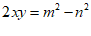 ;③
;③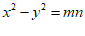 ;④
;④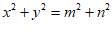 .
.
26. 小聪把一副三角尺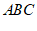 ,
,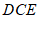 按如图1的方式摆放,其中边
按如图1的方式摆放,其中边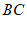 ,
,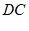 在同一条直线上,将其抽象出如图2的几何图形后,过点
在同一条直线上,将其抽象出如图2的几何图形后,过点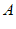 作射线
作射线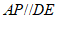 .
.
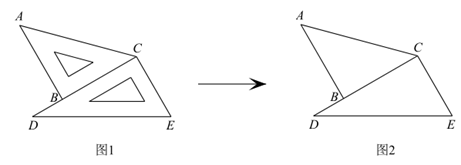
(1)依题意将图2补充完整;
(2)求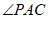 的度数。
的度数。
27.【概念学习】
定义:对于一个三位的自然数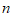 ,各数位上的数字都不为0,且百位数字与十位数字之和除以个位数字的商为整数,则称这个自然数
,各数位上的数字都不为0,且百位数字与十位数字之和除以个位数字的商为整数,则称这个自然数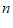 为“好数“.
为“好数“.
例如:714是“好数“,因为它是一个三位的自然数,7,1,4都不为0,且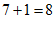 ,
,
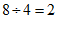 ,2为整数;
,2为整数;
643不是“好数“,因为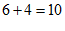 ,
,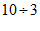 的商不是整数.
的商不是整数.
【初步探究】
(1)自然数312,675,981,802是“好数“的为______;
(2)在横线上填“真“或“假“:
①个位数字为1的一个三位自然数一定是“好数“是______命题;
②各数位上的数字都相同的一个三位自然数一定是“好数“是_____命题;
【深入思考】
求同时满足下列条件的“好数“:
(1)百位数字比十位数字大5;
(2)百位数字与十位数字之和等于个位数字.
28. 阅读下列材料:
我们知道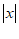 表示的是在数轴上数
表示的是在数轴上数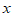 对应的点与原点的距离,即
对应的点与原点的距离,即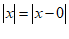 ,也就是说,
,也就是说,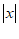 对表示在数轴上数
对表示在数轴上数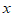 与数0对应点之间的距离.这个结论可以推广为
与数0对应点之间的距离.这个结论可以推广为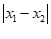 表示在数轴上数
表示在数轴上数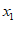 ,
,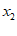 对应点之间的距离.
对应点之间的距离.
例1解方程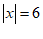 .
.
解:∵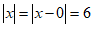 ,
,
∴在数轴上与原点距离为6的点对应的数为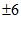 ,即该方程的解为
,即该方程的解为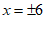 .
.
例2解不等式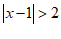 .
.
解:如图,首先在数轴上找出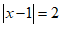 的解,即到1的距离为2的点对应的数为
的解,即到1的距离为2的点对应的数为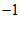 ,3,则
,3,则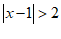 的解集为到1的距离大于2的点对应的所有数,所以原不等式的解集为
的解集为到1的距离大于2的点对应的所有数,所以原不等式的解集为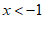 或
或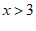 .
.

参考阅读材料,解答下列问题:
(1)方程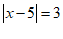 的解为______;
的解为______;
(2)解不等式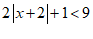 ;
;
(3)若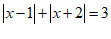 ,则
,则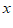 的取值范围是_______;
的取值范围是_______;
(4)若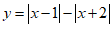 ,则
,则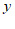 的取值范围是_______.
的取值范围是_______.
参考答案
一、选择题(本题共8道小题,每小题2分,共16分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | B | A | B | A | D | B | A | C |
二、填空题(本题共8道小题,每小题2分,共16分)
题号 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
答案 |
|
| 24,24 | 35 |
|
| 12 | 一班,四班 |
三、解答题(本题共12道小题,第17—22题,每小题5分,第23—26题,每小题6分,第27、28题,每小题7分,共68分)
17. 解: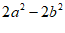
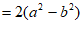 2分
2分
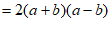 。 5分
。 5分
18. 解:原式=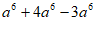 3分
3分
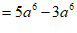 4分
4分
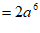 。 5分
。 5分
19. 解: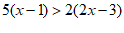 , 1分
, 1分
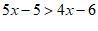 , 2分
, 2分
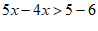 , 3分
, 3分
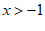 。 4分
。 4分
解集在数轴上表示为

20. 解: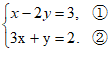
②×2,得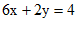 , ③ 1分
, ③ 1分
①+③,得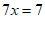 。 2分
。 2分
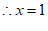 。 3分
。 3分
将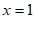 代入②,得
代入②,得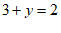 ,
,
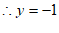 , 4分
, 4分
所以,原方程组的解为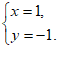 5分
5分
21. 解: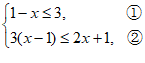
解不等式①,得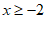 , 1分
, 1分
解不等式②,得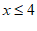 , 2分
, 2分
所以,原不等式组的解集为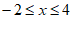 , 3分
, 3分
所以,整数解为-2,-1,0,1,2,3,4, 4分
所以,整数解的中位数为1。 5分
22. 解:原式=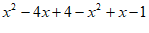 3分
3分
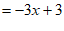 。 4分
。 4分
当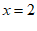 时,原式=-3。 5分
时,原式=-3。 5分
23. 解:(1)如下表。 2分
抽样调查50名初一学生最喜欢的居家健身项目人数统计表
活动项目 | 划记 | 频数 |
A. 平板支撑 |
| 4 |
B. 蹲起 |
| 8 |
C. 仰卧起坐 | 正正 | 10 |
D. 开合跳 |
| 18 |
E. 其他 | 正正 | 10 |
总计 | 50 |
(2)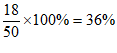 。 3分
。 3分
(3)校区4初一学生人数占集团初一学生总人数的20%。 4分
集团总人数: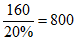 , 5分
, 5分
该集团初一学生中,最喜欢蹲起项目的人数约为800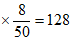 (人)。 6分
(人)。 6分
24. 解:我选择乙同学的思路。 1分
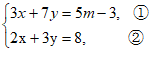
①+②,得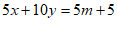 , 2分
, 2分
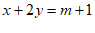 , ③ 3分
, ③ 3分
将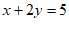 代入③,得
代入③,得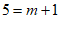 , 4分
, 4分
所以,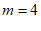 。 5分
。 5分
理由,此思路可以体现运算的简洁性。 6分
25. 解:(1)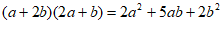 。 2分
。 2分
(2)需要三种纸片的块数如下:

3分
验证如下:
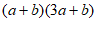
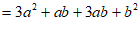 4分
4分
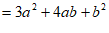 。 5分
。 5分
(3)①,③。 6分
26. 解:(1)依题意将图2补充完整。 1分
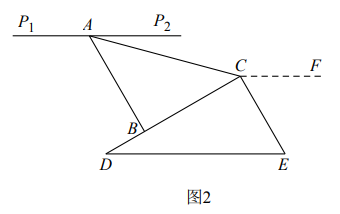
(2)过点C作CF∥DE, 2分
∴∠FCE=∠E=60°, 3分
∵∠ACB=45°,∠DCE=90°,
∴∠ACF=165°,
又∵AP∥DE,
∴AP∥CF。 4分
当点P在点A左侧时,∠PAC=∠ACF=165°, 5分
当点P在点A右侧时,∠PAC=180°-∠ACF=15°。 6分
27. 解:【初步探究】
(1)312,981。 2分
(2)①假,②真。 4分
【深入思考】
设十位数字为a,则百位数字为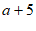 ,个数数字为
,个数数字为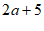 。 5分
。 5分
∵”好数”是三位的自然数,且各数位上的数字都不为0,
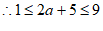 ,
,
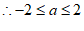 ,
,
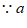 为正整数,
为正整数,
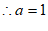 或2,
或2,
∴当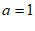 时,
时,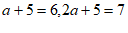 ;
;
当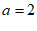 时,
时,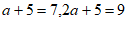 ,
,
∴满足条件的”好数”为617或729。 7分
28. 解:(1) 或
或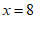 。 2分
。 2分
(2)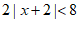 ,
,
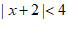 , 3分
, 3分
在数轴上找出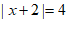 的解为-6或2, 4分
的解为-6或2, 4分
所以,原不等式的解集为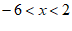 。 5分
。 5分
(3)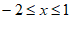 。 6分
。 6分
(4)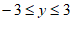 。 7分
。 7分
注:所有题选取其他思路酌情给分。