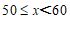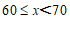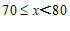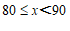北京市平谷区2020-2021学年下学期初中七年级期末调研数学试卷
本试卷共三道大题,27道小题,满分100分,考试时间120分钟。
一、选择题(本题共16分,每小题2分)
第1-8题均有四个选项,符合题意的选项只有一个.
1.平谷是中国著名的大桃之乡,每年4月桃花竞相开放,漫山遍野,如霞似锦,如海如潮,最是壮观。吸引无数市民和游客慕名前往。桃园内弥漫着桃花花粉,桃花花粉直径约为0.00003米,其中0.00003用科学记数法表示为
A.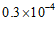 B.
B.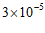
C.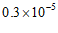 D.
D.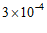
2.若实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是
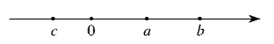
A.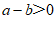 B.
B.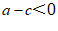 C.
C.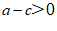 D.
D. 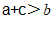
3.下列计算正确的是
A.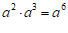 B.
B.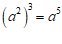
C.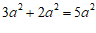 D.
D. 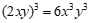
4. 在下列因式分解的过程中,分解因式正确的是
A.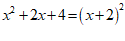 B.
B.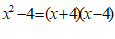
C.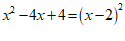 D.
D.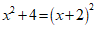
5. “十三五”时期是北京市迄今为止大气污染治理力度最大,成效最明显的五年,2020年空气质量优良天数继续增加,大气主要污染物中细颗粒物(PM2.5)年均浓度首次实现38微克/立方米,空气质量改善取得标志性、历史性突破。小明收集了2021年3月北京市16个城区的PM2.5的浓度均值(单位:微克/立方米),并整理如下表:
PM2.5的浓度 | 79 | 80 | 81 | 83 | 84 | 86 |
城区的个数 | 3 | 1 | 2 | 4 | 5 | 1 |
则北京市16个城区的PM2.5的浓度均值(单位:微克/立方米)的众数和中位数分别为
A.83,82 B.84,82 C.84,83 D.83,84
6. 关于命题”若 a=b,则|a|=|b|”与其逆命题的真假性,下列判断正确的是
A.原命题与其逆命题都是真命题
B.原命题与其逆命题都是假命题
C.原命题是假命题,其逆命题是真命题
D.原命题是真命题,其逆命题是假命题
7. 如图,将木条 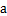 ,
,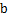 与
与 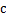 钉在一起,
钉在一起,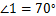 ,
,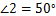 ,要使木条
,要使木条 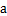 与
与 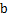 平行,木条
平行,木条 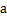 需顺时针旋转度数是
需顺时针旋转度数是
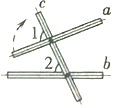
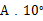 B.
B.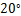
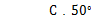
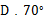
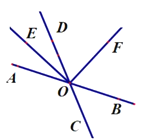
8.如图,直线 AB,CD 相交于点 O,分别作∠AOD,∠BOD 的平分线OE,OF. 将直线 CD 绕点 O 旋转,下列数据与∠BOD 大小变化无关的是
A. ∠AOD 的度数 B. ∠AOC 的度数
C. ∠EOF 的度数 D. ∠DOF 的度数
8.如图,直线 AB,CD 相交于点 O,OE平分∠AOD,OF平分∠BOD.当直线CD绕点O顺时针旋转α°(0<α<180)时,下列各角的度数与∠BOD度数变化无关的角是
A. ∠AOD B. ∠AOC C. ∠EOF D. ∠DOF
二、填空题(本题共16分,每小题2分)
9.用不等式表示:a的3倍与b的和不小于3
.
10. 如果把方程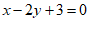 写成用含y的代数式表示x的形式,那么x =
写成用含y的代数式表示x的形式,那么x =
.
11.若多项式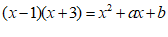 ,则
,则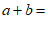
12.若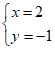 是方程
是方程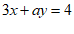 的解,则
的解,则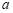 的值为
的值为
.
13.计算:(1)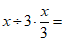
;
(2)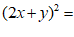
.字母的字体
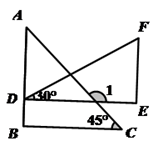
14. 将一副直角三角板如图摆放,点 D 落在 AB边上,BC∥DE,则∠1= °.
15. 已知方程组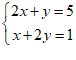 ,则
,则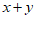 的值为_________.
的值为_________.
16.2020年比较流行一款推理类游戏,是用剧本虚拟出一场故事,玩家根据演绎和推理案件过程,得出结论.类比,此游戏过程,请同学们用扑克牌做一个简单的推理游戏:
①从左到右有三张不重复的扑克牌,这三张牌中不是红桃就是方块;
②红桃右边有且仅有一张方块;
③6的左边至少有一张是8;
④8的右边至少有一张是8.
请写出这三张牌从左到右的顺序可能是:
. (填写正确的序号)
红桃8,方块6,方块8 红桃8,红桃6,方块8 红桃8,方块8,红桃6

三、解答题(本题共68分,第17题10分,第18、19题,每题5分,第20题10分,第21、22题,每题5分,第23题6分,第24、25题,每小题5分,第26、27题,每小题6分)解答应写出文字说明、演算步骤或证明过程.
17.分解因式:
(1)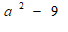
(2)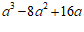 .
.
18.解不等式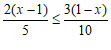 ,并求出非负整数解.
,并求出非负整数解.
19.解不等式组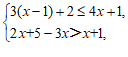 并把它的解集在数轴上表示出来.
并把它的解集在数轴上表示出来.
20.用适当的方法解下列方程组
(1)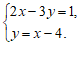 (2)
(2)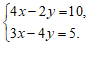
21.计算:
(1)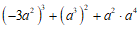
22.已知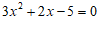 ,求代数式
,求代数式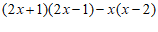 的值
的值
23.列方程(组)、解应用题
2021年4月世界休闲大会在北京平谷举办,本届大会秉承了”全域、全季、全民休闲”的理念,多角度呈现。大会的主会场馆-金海湖国际会展中心,位于金海湖畔,屹立于桃花海中,将为大家呈现了一幅用建筑写就的”山水画卷”。周末小明与父母去金海湖参观,在迎宾大道看到一种园艺造型, 他们一家子有如下交流:
(1)爸爸说:”如果搭配这个园艺造型需要花卉50盆,绿植90盆,每盆花卉的价格比每盆绿植的价格贵2元,而搭配这样一个园艺造型需要花费1500元,你知道每盆花卉和绿植各多少元吗?”请你帮小明解决此问题并写出求解过程.
(2)妈妈说:”若需要同样的花卉和绿植布置某个展厅,要求绿植比花卉多100盆,花费不低于6500元但也不能超过7000元,” 请你帮小明写出一种购买方案.
24.完成下面的证明:
已知:如图,AB∥CD,AD和BC交于点O,E为OA上一点,作∠AEF=∠AOB,交AB于点F.
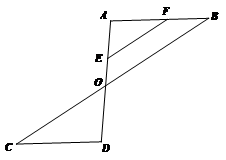
求证:∠EFA=∠C
证明:∵∠AEF=∠AOB,
∴
∥
( ).
∴∠EFA =∠B.
∵ AB∥CD,
∴∠B =∠C( ).
∴∠EFA=∠C( ).
25. 2021年平谷区创建文明城区的工作已全面启动。区教育系统结合《北京市生活垃圾管理条例》实施周年的重要节点,大力普及中学生垃圾分类知识,某校组织学生收集废弃塑料瓶活动以减少环境污染,现从七年级(2)班随机抽取了20名学生,对这20名学生一周内进行收集废弃塑料瓶活动的数量进行整理、描述和分析.下面给出了部分信息。
过程如下:
a.收集废弃塑料瓶的数量:
66 | 70 | 71 | 78 | 71 | 78 | 75 | 78 | 58 | 80 |
63 | 90 | 80 | 85 | 80 | 89 | 85 | 86 | 80 | 87 |
b、整理、描述数据:
数量 |
|
|
|
|
|
人数 | 1 | 2 | m | 9 | 1 |
c.收集废弃塑料瓶的数量统计图:
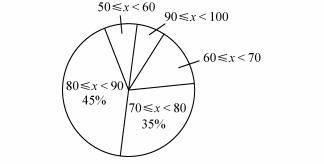
d.样本数据的平均数、中位数、众数如下表所示:
年级 | 平均数 | 中位数 | 众数 |
七年级(2)班 | 77.5 | n | k |
请根据所给信息,解答下列问题:
(1)m=
, n=
, k=
(2)在扇形统计图中,”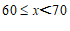 “所在的扇形的圆心角等于
“所在的扇形的圆心角等于
度;
(3)七年级共有200人,估计七年级收集数量不少于80个塑料瓶的学生总人数为
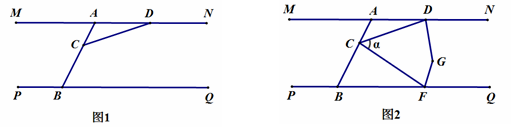
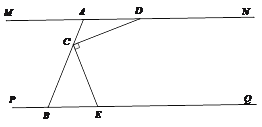
26.已知:直线MN、PQ被AB所截,且MN//PQ,点C是线段AB上一定点,点D是射线AN上一动点,连接CD.
(1)在图1中过点C作CE⊥CD,与射线BQ交于E点.
依题意补全图形;
求证:∠ADC+∠BEC=90°;
(2)如图2所示,点F是射线BQ上一动点,连接CF,∠DCF=α,分别作∠NDC与∠CFQ的角平分线交于点G,请用含有α的代数式来表示∠DGF,直接写出无需证明.
27.定义:若一个整数能表示成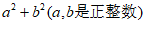 的形式,则称这个数为”完美数”.
的形式,则称这个数为”完美数”.
例如:因为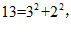 所以13是”完美数”;
所以13是”完美数”;
再如:因为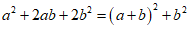 ,所以
,所以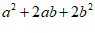 也是”完美数”.
也是”完美数”.
- 请直接写出一个小于10的”完美数”,这个”完美数”是
;
- 判断53
(请填写”是”或”否”)为”完美数”;
- 已知
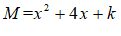
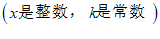 ,要使M为”完美数”,试求出符合条件的一个k值,并说明理由;
,要使M为”完美数”,试求出符合条件的一个k值,并说明理由;
- 如果数m,n都是”完美数”,试说明mn也是”完美数”.
【试题答案】
一、选择题(本题共16分,每小题2分)
题号
1
2
3
4
5
6
7
8
答案
B
C
D
A
C
B
D
C
二、填空题(本题共16分,每小题2分)
9.
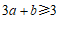
10.
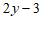
11.-1
12.
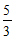
13.
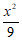 ;
;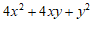
14.135
15.2 16.
三、解答题
 17.解:(1)原式
17.解:(1)原式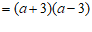
 (2)原式
(2)原式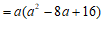 ⋯⋯⋯⋯⋯⋯⋯⋯⋯3分
⋯⋯⋯⋯⋯⋯⋯⋯⋯3分
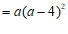 ⋯⋯⋯⋯⋯⋯⋯⋯⋯5分
⋯⋯⋯⋯⋯⋯⋯⋯⋯5分
 18.解:原式
18.解:原式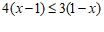
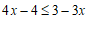 ⋯⋯⋯⋯⋯⋯⋯⋯⋯1分
⋯⋯⋯⋯⋯⋯⋯⋯⋯1分
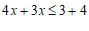 ⋯⋯⋯⋯⋯⋯⋯⋯⋯2分
⋯⋯⋯⋯⋯⋯⋯⋯⋯2分
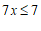 ⋯⋯⋯⋯⋯⋯⋯⋯⋯3分
⋯⋯⋯⋯⋯⋯⋯⋯⋯3分
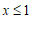 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯4分
. ⋯⋯⋯⋯⋯⋯⋯⋯⋯4分
所以,此不等式的解集是
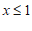 ,其中非负整数解为0,1. ⋯⋯⋯⋯⋯⋯⋯⋯⋯5分
,其中非负整数解为0,1. ⋯⋯⋯⋯⋯⋯⋯⋯⋯5分
19.解不等式组:
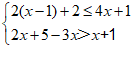
解①得,x≥-2 ⋯⋯⋯⋯⋯⋯⋯⋯⋯2分
解②得,x <2 ⋯⋯⋯⋯⋯⋯⋯⋯⋯3分
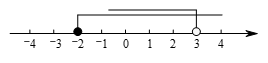 ⋯⋯⋯⋯⋯⋯⋯⋯⋯4分
⋯⋯⋯⋯⋯⋯⋯⋯⋯4分
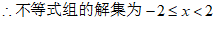 ⋯⋯⋯⋯⋯⋯⋯⋯⋯5分
⋯⋯⋯⋯⋯⋯⋯⋯⋯5分
 20.(1)解二元一次方程组
20.(1)解二元一次方程组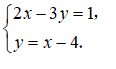
把代入得:
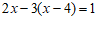
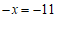
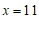 ⋯⋯⋯⋯⋯⋯⋯⋯⋯2分
⋯⋯⋯⋯⋯⋯⋯⋯⋯2分
将
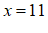 代入,得
代入,得 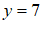 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯4分
. ⋯⋯⋯⋯⋯⋯⋯⋯⋯4分
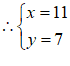 ⋯⋯⋯⋯⋯⋯⋯⋯⋯5分
⋯⋯⋯⋯⋯⋯⋯⋯⋯5分
(2)解二元一次方程组
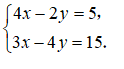
×2得:
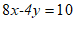 ⋯⋯⋯⋯⋯⋯⋯⋯⋯1分
⋯⋯⋯⋯⋯⋯⋯⋯⋯1分-得
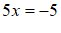 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯2分
. ⋯⋯⋯⋯⋯⋯⋯⋯⋯2分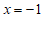 ⋯⋯⋯⋯⋯⋯⋯⋯⋯3分
⋯⋯⋯⋯⋯⋯⋯⋯⋯3分将
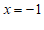 代入①,得
代入①,得 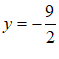 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯4分
. ⋯⋯⋯⋯⋯⋯⋯⋯⋯4分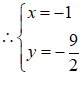 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯5分
. ⋯⋯⋯⋯⋯⋯⋯⋯⋯5分21.原式
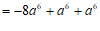 ⋯⋯⋯⋯⋯⋯⋯⋯⋯3分
⋯⋯⋯⋯⋯⋯⋯⋯⋯3分
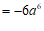
22.原式
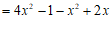 ⋯⋯⋯⋯⋯⋯⋯⋯⋯2分
⋯⋯⋯⋯⋯⋯⋯⋯⋯2分
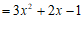 ⋯⋯⋯⋯⋯⋯⋯⋯⋯3分
⋯⋯⋯⋯⋯⋯⋯⋯⋯3分
由
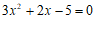
得
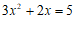 ⋯⋯⋯⋯⋯⋯⋯⋯⋯4分
⋯⋯⋯⋯⋯⋯⋯⋯⋯4分
 原式
原式 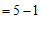
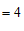
23.(1)解:设每盆绿植的价格为x元,则每盆花卉的价格为(x+2)元.
根据题意列方程,得: ⋯⋯⋯⋯⋯⋯⋯⋯⋯1分
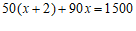 ⋯⋯⋯⋯⋯⋯⋯⋯⋯2分
⋯⋯⋯⋯⋯⋯⋯⋯⋯2分
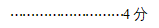 解方程得:
解方程得: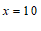 .
.
所以:x+2=12
答:每盆绿植的价格为10元,则每盆花卉的价格为12元.
(2)解:设需要花卉y盆,则需要绿植(y+100)盆.
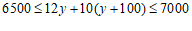 ⋯⋯⋯⋯⋯⋯⋯⋯⋯5分
⋯⋯⋯⋯⋯⋯⋯⋯⋯5分
解得:
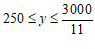
答:需要花卉250--272盆,对应需要绿植350--372盆任意一种即可 ⋯⋯⋯⋯⋯⋯⋯6分
24.∵∠AEF=∠AOB,
∴EF∥OB(同位角相等,两直线平行).⋯⋯⋯⋯⋯⋯3分
∴∠EFA =∠B.
∵ AB∥CD,
∴∠B =∠C.(两直线平行,内错角相等).⋯⋯⋯⋯⋯⋯⋯⋯⋯4分
∴∠EFA=∠C( 等量代换 ).⋯⋯⋯⋯⋯⋯⋯⋯⋯5分
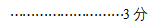 25. (1) m=7 , n= 79 , k= 80
25. (1) m=7 , n= 79 , k= 80
(2) 在扇形统计图中,”
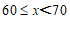 “所在的扇形的圆心角等于 36 度;⋯⋯⋯4分
“所在的扇形的圆心角等于 36 度;⋯⋯⋯4分
(3)七年级共有200人,估计七年级收集数量不少于80个塑料瓶的学生总人数为 100人 ⋯⋯⋯⋯⋯⋯⋯⋯⋯5分
26.
(1)
⋯⋯⋯1分
(2)证明:过点C作CH∥MN ⋯⋯⋯2分
∵CH∥MN
∴∠ADC=∠DCH ⋯⋯⋯3分
∵PQ∥MN
∴PQ∥CH
∴∠BEC=∠ECH ⋯⋯⋯4分
∵∠DCH+∠ECH=∠DCE=90°
∴∠ADC+∠BEC=90°
⋯⋯⋯5分
(3)
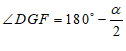
⋯⋯⋯6分
27.(1)请直接写出一个小于10的”完美数”,这个”完美数”是 5 ;⋯⋯⋯1分
(2)判断53 是 (请填写”是”或”否”)为”完美数”; ⋯⋯⋯2分
(3)当k=5时(不固定,符合条件即可) ⋯⋯⋯3分
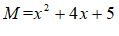
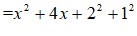
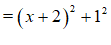 ⋯⋯⋯4分
⋯⋯⋯4分
∴当k=5时,M为”完美数”
(4)如果数m,n都是”完美数”,试说明mn也是”完美数”.
设
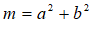 ,
,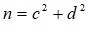 ⋯⋯⋯5分
⋯⋯⋯5分
∴
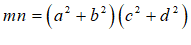
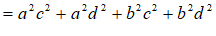
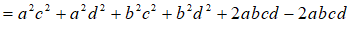
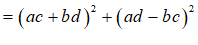 ⋯⋯⋯6分
⋯⋯⋯6分
∴mn也是”完美数”