北京市丰台区2020-2021学年下学期初中七年级期末练习数学试卷
本试卷满分100分。考试时间90分钟。
一、选择题(本题共30分,每小题3分)
下列各题均有四个选项,其中只有一个是符合题意的.
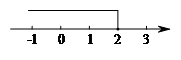
1.数轴上表示的不等式的解集正确的是
A. 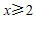 B.
B. 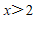 C.
C. 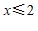 D.
D. 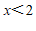
2.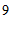 的平方根是
的平方根是
A. 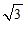 B.
B. 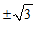 C.
C. 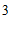 D.
D. 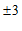
3.如图,直线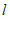 与直线
与直线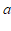 ,
,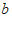 相交,且
相交,且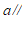
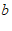 ,如果∠1
,如果∠1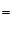 110º,那么∠2的度数是
110º,那么∠2的度数是
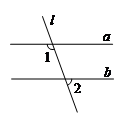
A. 20° B. 70° C. 90° D. 110°
4.空气是由多种气体混合而成,为了直观地介绍空气各成分的百分比,最适合使用的统计图是
A. 条形图 B. 折线图 C. 扇形图 D. 直方图
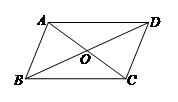
5.如图,四边形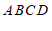 中,
中,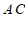 ,
,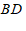 交于点
交于点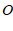 ,如果
,如果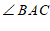
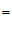
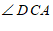 ,那么以下四个结论中错误的是
,那么以下四个结论中错误的是
A. 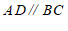 B.
B. 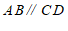
C. 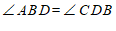 D.
D. 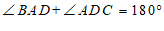
6.如果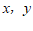 满足方程组
满足方程组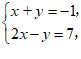 那么
那么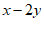 的值是
的值是
A. 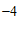 B.
B. 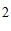 C.
C. 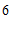 D.
D. 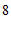
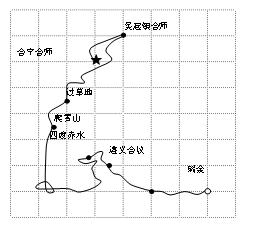
7.2021年是中国共产党建党100周年暨红军长征胜利85周年.长征是中国共产党和中国革命事业从挫折走向胜利的伟大转折点.下图是红一方面军长征路线图,如果表示瑞金的点的坐标为(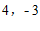 ),表示遵义会议的点的坐标为(
),表示遵义会议的点的坐标为(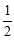 ,
,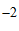 ),那么表示吴起镇会师的点的坐标为
),那么表示吴起镇会师的点的坐标为
A. (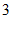 ,
,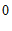 ) B. (
) B. (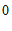 ,
,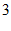 ) C. (
) C. (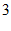 ,
,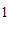 ) D. (
) D. (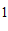 ,
,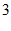 )
)
8.明代数学家程大位的著作《算法统综》中有一个”绳索量竿”问题:”一只竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托,问索长几尺?”
译文为:”现有一根竹竿和一条绳索,用绳索去量竹竿,绳索比竹竿长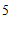 尺,如果将绳索对折后再去量竹竿,就比竹竿短5尺,问绳索长几尺?”(注:一托=
尺,如果将绳索对折后再去量竹竿,就比竹竿短5尺,问绳索长几尺?”(注:一托=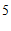 尺)
尺)
设绳索长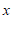 尺,竹竿长
尺,竹竿长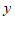 尺,根据题意列方程组正确的是
尺,根据题意列方程组正确的是
A. 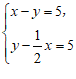 B.
B. 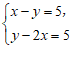 C.
C. 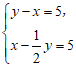 D.
D. 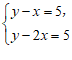
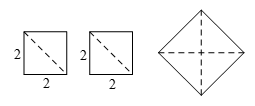
9.如图,用边长为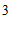 的两个小正方形拼成一个大正方形,
的两个小正方形拼成一个大正方形,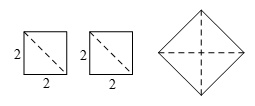
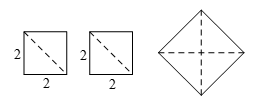 则大正方形的边长最接近的整数是
则大正方形的边长最接近的整数是
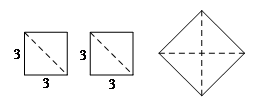
A. 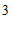 B.
B. 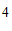 C.
C. 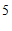 D.
D. 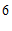
10.已知关于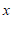 的不等式组
的不等式组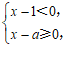 有以下说法:
有以下说法:
①如果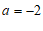 ,那么不等式组的解集是
,那么不等式组的解集是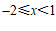
 ②如果不等式组的解集是
②如果不等式组的解集是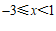 ,那么
,那么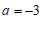
③如果不等式组的整数解只有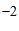 ,
,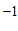 ,
,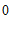 ,那么
,那么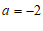
④如果不等式组无解,那么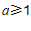
其中所有正确说法的序号是
A. ①②③ B. ①②④ C. ①③④ D. ②③④
二、填空题(本题共18分,每小题3分)
11.如果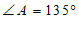 ,那么
,那么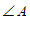 的邻补角的度数为
的邻补角的度数为
 .
.
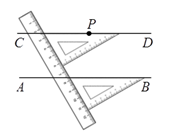
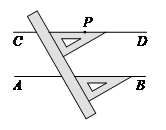
12.如图,利用直尺和三角板,过直线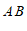 外一点
外一点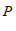 画直线
画直线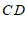 ,使
,使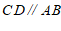 ,画图的依据是
,画图的依据是
.
13.如果点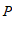 (
(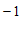 ,
,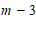 )到
)到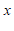 轴的距离等于
轴的距离等于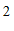 ,那么
,那么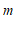 的值为
的值为
.
14.写出一个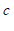 的值,说明命题”如果
的值,说明命题”如果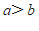 ,那么
,那么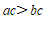 “是假命题,这个值可以是
“是假命题,这个值可以是
.
15.某日小王驾驶一辆小型车到某地办事,上午9:00到达,在路边的电子收费停车区域内停车.收费标准如图:
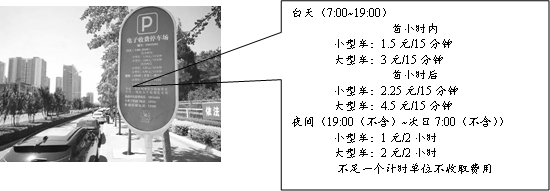
(1)如果他9:50离开,那么应缴费
元;
(2)如果他离开时缴费15元,那么停车的时长可能是
分钟.
(写出一个即可)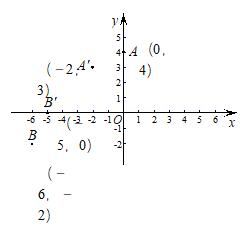
 16.在平面直角坐标系
16.在平面直角坐标系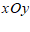 中,对点
中,对点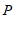 进行如下操作:把点
进行如下操作:把点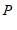 的横、纵坐标乘以同一个实数
的横、纵坐标乘以同一个实数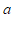 ,将得到的点先向左平移
,将得到的点先向左平移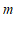 个单位长度,再向上平移
个单位长度,再向上平移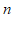 个单位长度,得到点
个单位长度,得到点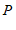 的对应点
的对应点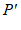 .如图,点
.如图,点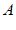 ,
,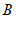 经过上述操作后得到的对应点分别是点
经过上述操作后得到的对应点分别是点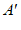 ,
,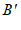 .
.
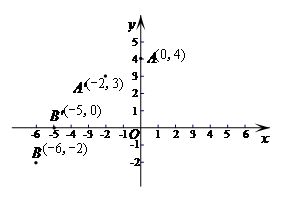
 (1)如果点 (
(1)如果点 (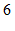 ,
,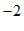 )经过上述操作后得到的对应点是点
)经过上述操作后得到的对应点是点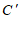 ,那么点
,那么点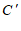 的坐标为
的坐标为
;
- 如果点
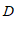 经过上述操作后得到的对应点
经过上述操作后得到的对应点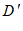 与点
与点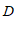 重合,那么点
重合,那么点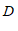 的坐标为
的坐标为
.
三、解答题(本题共52分,第17-23,25题,每小题5分,第24,26题,每小题6分)
17.计算:
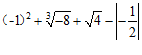 .
.
18.解方程组:
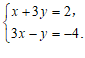
19.解不等式组:
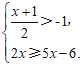
20.在平面直角坐标系
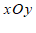 中,已知点
中,已知点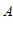 (
(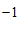 ,
,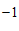 ),
),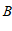 (
(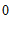 ,
,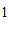 ).
).
(1)将线段
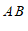 向右平移
向右平移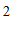 个单位长度,向下平移
个单位长度,向下平移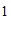 个单位长度,平移后得到对应线段
个单位长度,平移后得到对应线段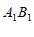 ,请画出线段
,请画出线段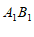 ,并写出点
,并写出点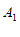 ,
,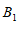 的坐标;
的坐标;
(2)平移线段
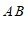 得到线段
得到线段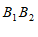 ,使得点
,使得点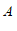 与点
与点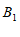 重合,写出一种由线段
重合,写出一种由线段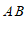 得到线段
得到线段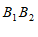 的运动过程.
的运动过程.
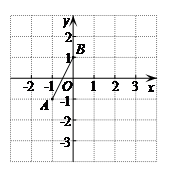
21.为贯彻落实教育部印发的《大中小学劳动教育指导纲要(试行)》通知要求,培养学生劳动习惯与劳动能力,某校学生发展中心在暑假期间开展了”家务劳动我最行”的实践活动.开学后从本校七至九年级各随机抽取30名学生,对他们的每日平均家务劳动时长(单位:min)进行了调查,并对数据进行了收集、整理和描述.下面是其中的部分信息:
a.
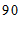 名学生每日平均家务劳动时长的频数分布表:
名学生每日平均家务劳动时长的频数分布表:
分组
频数
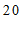 ≤x<
≤x<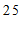
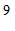
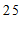 ≤x<
≤x<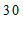
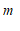
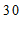 ≤x<
≤x<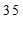
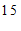
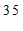 ≤x<
≤x<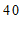
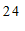
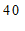 ≤x<
≤x<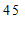
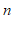
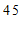 ≤x<
≤x<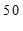
合计
 b.
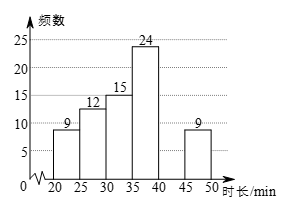
b.  名学生每日平均家务劳动时长频数分布直方图:
名学生每日平均家务劳动时长频数分布直方图:
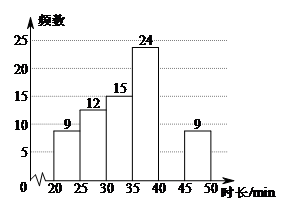
c. 每日平均家务劳动时长在
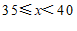 这一组的是:
这一组的是:
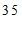
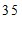
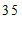
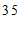
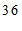
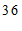
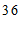
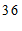
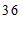
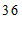
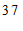
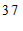
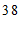
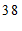
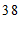
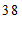
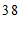
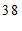
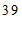
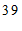
d. 小东每日平均家务劳动时长为
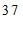 min.
min.
根据以上信息,回答下列问题:
(1)写出频数分布表中的数值m =
,n =
;
(2)补全频数分布直方图;
(3)小东每日平均家务劳动时长
样本中一半学生的每日平均家务劳动时长;(填”超过”或”没超过”)
(4)学生发展中心准备将每日平均家务劳动时长达到40min及以上的学生评为”家务小能手”,如果该校七至九年级共有420名学生,请估计获奖的学生人数.
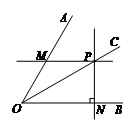
22.如图,点
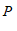 为
为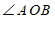 的角平分线
的角平分线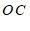 上的一点,过点
上的一点,过点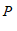 作
作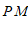 ∥
∥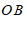 交
交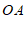 于点
于点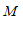 ,过点
,过点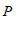 作
作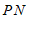 ⊥
⊥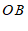 于点
于点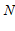 .当
.当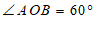 时,求∠
时,求∠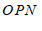 的度数.
的度数.
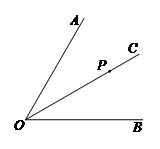
(1)依题意,补全图形;
(2)完成下面的解题过程.
解:∵
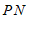 ⊥
⊥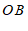 于点
于点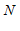 ,
,
∴∠
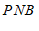
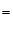
°(
)(填推理的依据).
∵
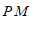 ∥
∥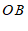 ,
,
∴∠
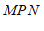
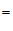 ∠
∠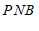
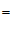
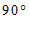 ,
,
∠
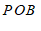
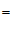
(
)(填推理的依据).
∵
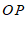 平分
平分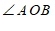 ,且
,且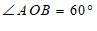 ,
,
∴∠POB
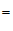
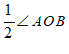
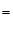 30°(角的平分线的定义).
30°(角的平分线的定义).
∴
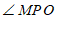
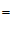
°.
∵
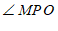 +
+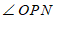
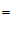 ∠
∠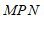 ,
,
∴
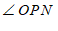
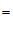
°.
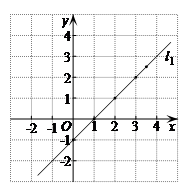
23.在平面直角坐标系
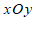 中,二元一次方程的一个解可以用一个点表示,以二元一次方程的解为坐标的点的全体叫做这个方程的图象.例如
中,二元一次方程的一个解可以用一个点表示,以二元一次方程的解为坐标的点的全体叫做这个方程的图象.例如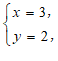 是方程
是方程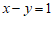 的一个解,用一个点(
的一个解,用一个点( ,
,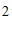 )来表示,以方程
)来表示,以方程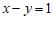 的解为坐标的点的全体叫做方程
的解为坐标的点的全体叫做方程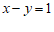 的图象,方程
的图象,方程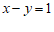 的图象是图中的直线
的图象是图中的直线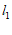 .
.
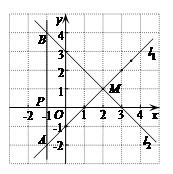
(1)二元一次方程
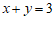 的图象是直线
的图象是直线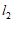 ,在同一坐标系中画出这个方程的图象;
,在同一坐标系中画出这个方程的图象;
(2)写出直线
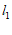 与直线
与直线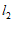 的交点
的交点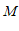 的坐标;
的坐标;
(3)过点
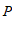 (
(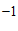 ,
,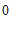 )且垂直于
)且垂直于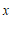 轴的直线与
轴的直线与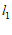 ,
,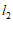 的交点分别为
的交点分别为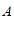 ,
,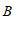 ,直接写出三角形
,直接写出三角形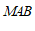 的面积.
的面积.
24.课上教师呈现一个问题:
如图,
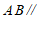
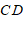 ,点
,点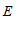 是线段
是线段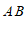 ,
,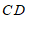 所在直线
所在直线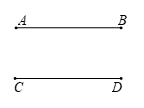 外的一点,连接
外的一点,连接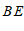 ,
,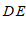 ,探究∠
,探究∠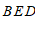 ,∠
,∠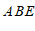 ,∠
,∠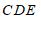 之间的数量关系.
之间的数量关系.
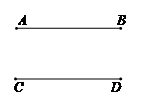
小凯画出了图
 ,图
,图 ,分析思路及结论如下:
,分析思路及结论如下:
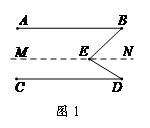
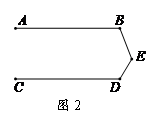
分析思路:
要寻求三个角之间的数量关系,根据图中角的位置特征,可以借助平行线进行角的位置的转换.
如图
 ,过点
,过点 作
作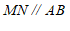 .
.
(1)由
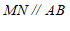 可知∠
可知∠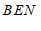
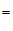 ∠
∠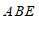 ;
;
(2)由
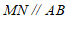 ,
,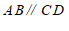 得到
得到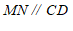 ,
,
可知∠
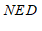
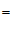 ∠
∠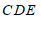 ;
;
(3)由∠
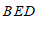
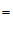 ∠
∠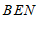 +∠
+∠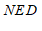 ,
,
得到结论:∠
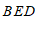
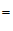 ∠
∠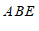 +∠
+∠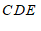 .
.
如图2,类似图1的分析……
得到结论:∠
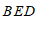 +∠
+∠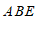 +∠
+∠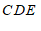
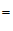
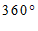 .
.
小明认为小凯只考虑了点
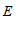 在直线
在直线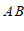 ,
,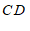 之间的情况,点
之间的情况,点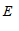 的位置应该还有其他情况.
的位置应该还有其他情况.
根据以上材料,解答问题:
画出一种点
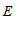 不在直线
不在直线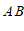 ,
,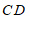 之间的图形,写出探究∠
之间的图形,写出探究∠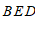 ,∠
,∠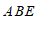 ,∠
,∠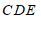 之间的数量关系的分析思路及结论.
之间的数量关系的分析思路及结论.
25.”冰墩墩”和”雪容融”分别是北京
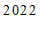 年冬奥会和冬残奥会的吉祥物.自
年冬奥会和冬残奥会的吉祥物.自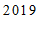 年正式亮相后,相关特许商品投放市场,持续热销.某冬奥官方特许商品零售店购进了一批同一型号的”冰墩墩”和”雪容融”玩具,连续两个月的销售情况如下表:
年正式亮相后,相关特许商品投放市场,持续热销.某冬奥官方特许商品零售店购进了一批同一型号的”冰墩墩”和”雪容融”玩具,连续两个月的销售情况如下表:

月份
销售量/件
销售额/元
冰墩墩
雪容融
第
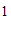 个月
个月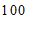
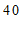
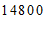
第2个月
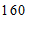
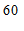
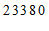
(1)求此款”冰墩墩”和”雪容融”玩具的零售价格;
(2)某单位欲购买这两款玩具作为冬奥知识竞赛活动的奖品,要求”雪容融”的数量恰好等于”冰墩墩”的数量的
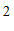 倍,且购买总资金不得超过
倍,且购买总资金不得超过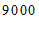 元,请根据要求确定该单位购买”冰墩墩”玩具的最大数量.
元,请根据要求确定该单位购买”冰墩墩”玩具的最大数量.
26.在平面直角坐标系
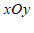 中,已知点
中,已知点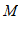 (
(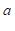 ,
,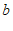 ).如果存在点N(
).如果存在点N(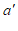 ,
,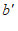 ),满足
),满足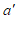 =
=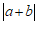 ,
,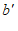 =
=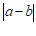 ,则称点
,则称点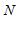 为点
为点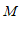 的”控变点”.
的”控变点”.
(1)点
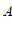 (
(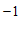 ,
,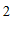 )的”控变点”
)的”控变点”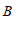 的坐标为
的坐标为
;
(2)已知点
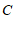 (
(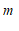 ,
,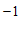 )的”控变点”
)的”控变点”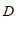 的坐标为(
的坐标为(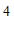 ,
,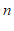 ),求
),求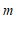 ,
,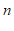 的值;
的值;
(3)长方形
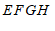 的顶点坐标分别为(
的顶点坐标分别为(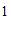 ,
,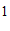 ),(
),(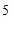 ,
,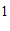 ),(
),(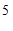 ,
,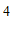 ),(
),(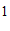 ,
,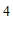 ).
).
如果点
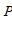 (
(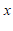 ,
,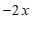 )的”控变点”
)的”控变点”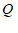 在长方形
在长方形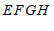 的内部,直接写出
的内部,直接写出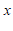 的取值范围.
的取值范围.
【试题答案】
一、选择题(本题共30分,每小题3分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
D
B
C
A
D
D
A
B
B
二、填空题(本题共18分,每小题3分)
11.45° 12.同位角相等,两直线平行 13.5或1 14.
 1(答案不唯一) 15.(1)4.5 (2)120 (答案不唯一) 16.(1)(1,0) (2)(
1(答案不唯一) 15.(1)4.5 (2)120 (答案不唯一) 16.(1)(1,0) (2)( 4,2)
4,2)
三、解答题(本题共52分,第17-23,25题,每小题5分,第24,26题,每小题6分)
- 解:原式=
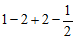 , ……4分
, ……4分
=
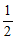 . ……5分
. ……5分
- 解:
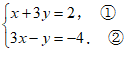
由①,得
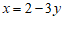 .③ ……1分
.③ ……1分
把③代入②,
得
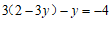 . …… 2分
. …… 2分
解得
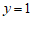 . ……3分
. ……3分
把
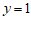 代入③,解得
代入③,解得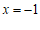 .……4分
.……4分
∴原方程组的解为
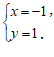 ……5分
……5分
- 解:
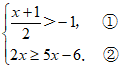
解不等式①,得
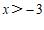 . ……2分
. ……2分
解不等式②,得
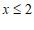 . ……4分
. ……4分
不等式组的解集在数轴上表示如下:
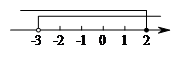
∴不等式组的解集为
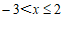 .…5分
.…5分
20. 解:(1)正确画出线段A1B1; ……2分
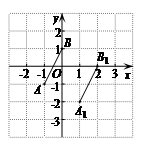
A1(1,-2),B1(2,0);……3分
(2)线段AB先向右平移3个单位长度,再向上平移1个单位长度得到线段B1B2. (答案不唯一)……5分
21. 解:(1)m= 12 ,n= 21 ;……2分
(2)正确补全图形; ……3分
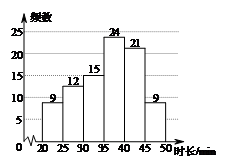
(3)超过; ……4分
(4)140人. ……5分
22.解:(1)正确补全图形; ……1分
(2)解:∵PN⊥OB于点N,
∴∠PNB = 90°(垂直的定义).2分
∵PM∥OB,
∴∠MPN=∠PNB= 90°.
∠POB = ∠MPO
.
( 两直线平行,内错角相等 ).3分
∵OP平分∠AOB,且∠AOB=60°,
∴∠POB=
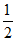 ∠AOB= 30°
∠AOB= 30°
(角的平分线的定义).
∴∠MPO= 30 °. ……4分
∵∠MPO+∠OPN=∠MPN,
∴∠OPN= 60 °. ……5分
23.(1)正确画出图象; ……2分
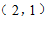 ; ……3分
; ……3分
- 9. ……5分
 解:如图,
解:如图,
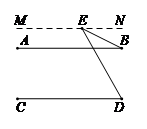
……1分
分析思路:
过点E作MN∥AB. ……2分
(1)由MN∥AB可知∠BEN=∠ABE; ……3分
(2)由MN∥AB,AB∥CD得到MN∥CD,可知∠NED=∠CDE; ……4分
(3)由∠BED=∠NED
 ∠BEN , ……5分
∠BEN , ……5分
得到结论:∠BED=∠CDE
 ∠ABE. ……6分
∠ABE. ……6分
25. 解:(1)设”冰墩墩”玩具的零售价为x元,”雪容融”玩具的零售价为y元.
……1分
根据题意,列出方程组:
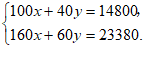 ……2分
……2分
解方程组,得
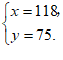
答:”冰墩墩”玩具的零售价为118元,”雪容融”玩具的零售价为75元. …3分
(2)设该单位可买a件”冰墩墩”玩具.
根据题意,可列出不等式:118a+
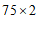 a≤9000, ……4分
a≤9000, ……4分
解不等式 ,得a≤33
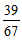 .
.
答:该单位最多购买33件”冰墩墩”玩具. ……5分
26. 解:(1)(1,3); ……1分
(2)根据定义可知
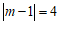 ,解得m=5或m=
,解得m=5或m= 3.
3.
当m=5时,
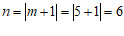 ;
;
当m=
 3时,
3时,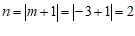 .
.
∴
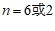 . ……4分
. ……4分
(3)
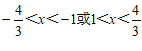 . ……6分
. ……6分
