北京101中学2020-2021学年下学期高一年级期末考试数学试卷
一、选择题:共10小题。在每小题列出的四个选项中,选出符合题目要求的一项。
1.已知z=2−i,则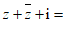 ( )
( )
(A)2−2i (B)4−i (C)2+2i (D)4+i
2.下列区间中,函数f(x)=7sin(x−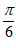 )单调递增的区间是( )
)单调递增的区间是( )
(A)(0,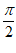 ) (B)(
) (B)(
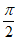 ,π) (C)(π,
,π) (C)(π,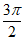 ) (D)(
) (D)(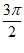 ,2π)
,2π)
3.在△ABC中,已知a=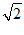 ,b=2,B=45°,则A=( )
,b=2,B=45°,则A=( )
(A)30°或60° (B)30° (C)60°或120° (D)150°
4.设平面α与平面β相交于直线m,直线a在平面α内.直线b在平面β内,且b⊥m,则“α⊥β”是“a⊥b“的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
5.在△ABC中,C=90°,AC=4,BC=3,点P是AB的中点,则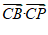 =( )
=( )
(A)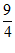 (B)4 (C)
(B)4 (C)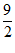 (D)6
(D)6
6.已知α,β是两个不同的平面,m,n是两条不同的直线,下列命题中错误的是( )
(A)若m⊥α,n∥m,n⊂β,则α⊥β
(B)若m⊂α,α∥β,n⊂β,则n∥m
(C)若m⊥α,α∥β,n⊥β,则n∥m
(D)若β⊥α,α∩β=n,m⊂α,n⊥m,则m⊥β
7.若tanθ=−2,则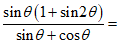 ( )
( )
(A)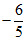 (B)
(B)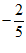 (C)
(C)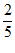 (D)
(D)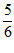
8.为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
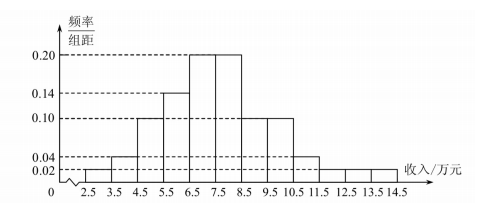
根据此频率分布直方图,下面结论中不正确的是( )
(A)该地农户家庭年收入低于4.5万元的农户比率估计为6%
(B)该地农户家庭年收入不低于10.5万元的农户比率估计为10%
(C)估计该地农户家庭年收入的平均值不超过6.5万元
(D)估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
9.如图,在空间四边形ABCD中,两条对角线AC,BD互相垂直,且长度分别为4和6,平行于这两条对角线的平面与边AB,BC,CD,DA分别相交于点E,F,G,H,记四边形EFGH的面积为y,设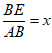 ,则( )
,则( )
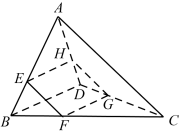
(A)函数y=f(x)的值域为(0,4] (B)函数y=f(x)的最大值为8
(C)函数y=f(x)在(0,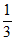 )上单调递增 (D)函数y=f(x)满足f(x)=f(
)上单调递增 (D)函数y=f(x)满足f(x)=f(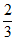 −x)
−x)
10.有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回的随机取两次,每次取1个球,甲表示事件“第一次取出的球的数字是1″,乙表示事件“第二次取出的球的数字是2″,丙表示事件“两次取出的球的数字之和是8″,丁表示事件“两次取出的球的数字之和是7″,则( )
(A)甲与丙相互独立 (B)甲与丁相互独立
(C)乙与丙相互独立 (D)丙与丁相互独立
二、填空题:共6小题。
11.设a∈R.若复数(1+i)(a+i)在复平面内对应的点位于实轴上,则a=____________.
12.若A为△ABC的内角,且sin2A=−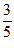 ,则cos(A+
,则cos(A+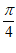 )的值为____________.
)的值为____________.
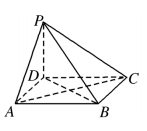
13.如图,已知PD垂直于正方形ABCD所在的平面,连接PB,PC,PA,AC,BD,则一定互相垂直的平面有____________对.
14.已知不等式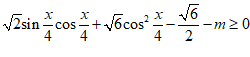 对于
对于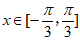 恒成立,则实数m的取值范围是____________.
恒成立,则实数m的取值范围是____________.
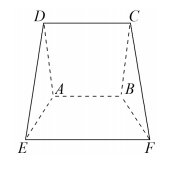
15.中国古代数学名著《九章算术》中记载:”今有羡除“.刘徽注:”羡除,隧道也.其所穿地,上平下邪.“现有一个羡除如图所示,四边形ABCD,ABFE,CDEF均为等腰梯形,AB∥CD∥EF,AB=6,CD=8,EF=10,EF到平面ABCD的距离为3,CD与AB间的距离为10,则这个羡除的体积是____________.
16.已知函数f(x)=|sinx|cosx,给出下列五个结论:
①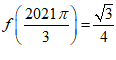 ; ②若|f(x1)|=|f(x2)|,则x1=x2+kπ(k∈Z);
; ②若|f(x1)|=|f(x2)|,则x1=x2+kπ(k∈Z);
③f(x)在区间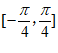 上单调递增; ④函数f(x)的周期为π;
上单调递增; ④函数f(x)的周期为π;
⑤f(x)的图像关于点(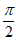 ,0)成中心对称.
,0)成中心对称.
其中正确的结论的序号是____________.
三、解答题:共4小题。解答应写出文字说明、演算步骤或证明过程。
17.在△ABC中,c=2,C=30°.再从条件①、条件②、条件③这三个条件中选择一个作为已知,使其能够确定唯一的三角形,求:
(1)a的值;
(2)△ABC的面积.
条件①:
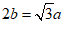 ;条件②:
;条件②:
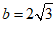 ;条件③:A=45°.
;条件③:A=45°.
18.为迎接2022年北京冬季奥运会,普及冬奥知识,某地区小学联合开展了“冰雪答题王“冬奥知识竞赛活动.现从参加该活动的学生中随机抽取了30名学生,将他们的竞赛成绩(单位:分)用茎叶图记录如下:
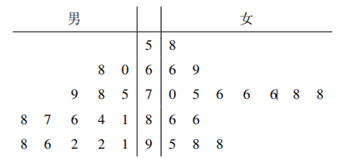
(1)从该地区参加该活动的男生中随机抽取1人,估计该男生的竞赛成绩在90分以上的概率;
(2)从该地区参加该活动的全体男生中随机抽取2人,全体女生中随机抽取2人,估计这4人中男生竞赛成绩在90分以上的人数比女生竞赛成绩在90分以上的人数多的概率;
(3)为便于普及冬奥知识,现从该地区某所小学参加冬奥知识竞赛活动的学生中随机选取10名男生、10名女生作为冬奥宣传志愿者,记这10名男生竞赛成绩的平均数为µ1,这10名女生竞赛成绩的平均数为µ2,能否认为µ1>µ2,说明理由.
19.已知正四棱柱ABCD−A1B1C1D1中,M是DD1的中点.
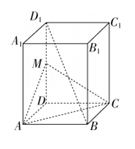
(1)求证:BD1∥平面AMC;
(2)求证:AC⊥BD1;
(3)在线段BB1上是否存在点P,当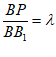 时,平面A1PC1∥平面AMC?若存在,求出λ的值并证明;若不存在,请说明理由.
时,平面A1PC1∥平面AMC?若存在,求出λ的值并证明;若不存在,请说明理由.
20.对n∈N∗,定义an(x)=
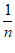 (sin2x−cosnx).
(sin2x−cosnx).
(1)求a2(x)−a1(x)的最小值;
(2)∀n∈N∗,有an(x)≥A恒成立,求A的最大值;
(3)求证:不存在m,n∈N∗,且m>n,使得am(x)−an(x)为恒定常数.
参考答案
1.D 2.A 3.B 4.A 5.C 6.B 7.C 8.D 9.C 10.B
11.−1. 12.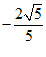 . 13.7. 14.(−∞,
. 13.7. 14.(−∞,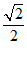 ]. 15.120. 16.①⑤.
]. 15.120. 16.①⑤.
17.选择条件①:2b=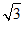 a.
a.
(1)在△ABC中,因为2b=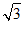 a,所以b=
a,所以b=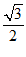 a.
a.
因为c=2,C=30°,
根据余弦定理:
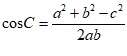 ,得
,得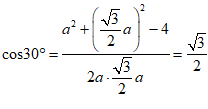 ,
,
整理,得a2=16,由于a>0,所以a=4.
(2)由(1)可知,b=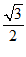 a=2
a=2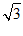 .
.
因为a=4,c=2,所以a2=b2+c2.所以A=90°.
因此,△ABC是直角三角形.
所以S=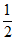 bc=
bc=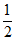 ×2
×2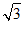 ×2=2
×2=2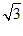 .
.
选择条件②:不给分.
选择条件③:A=45°.
(1)在△ABC中,因为A=45°,C=30°,c=2,
根据正弦定理:
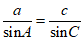 ,所以
,所以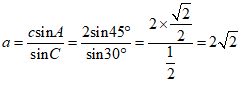 .
.
(2)在△ABC中,因为sinB=sin(A+C),
所以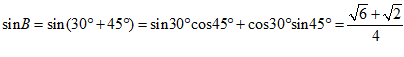 .
.
所以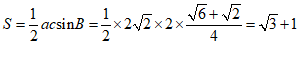 .
.
18.(1)由茎叶图可知,随机抽取的30名学生中男生有15名,其中竞赛成绩在90分以上的学生有5名.
所以随机抽取的15名男生中竞赛成绩在90分以上的频率为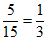 .
.
所以从该地区参加该活动的男生中随机抽取1人,该男生的竞赛成绩在90分以上的概率估计为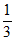 .
.
(2)记Ai(i=1,2)表示“第i名男生的竞赛成绩在90分以上“,Bj(j=1,2)表示“第j名女生的竞赛成绩在90分以上“,C表示“4人中男生竞赛成绩在90分以上的人数比女生竞赛成绩在90分以上的人数多“.
同(1),从该地区参加该活动的女生中随机抽取1人,该女生竞赛成绩在90分以上的概率估计为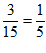 ,
,
则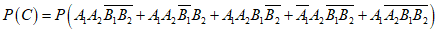
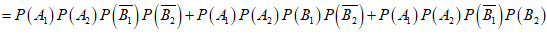
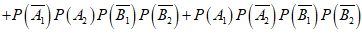
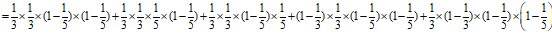
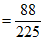 .
.
(3)参考答案:不能确定是否有µ1>µ2.
上述10名男生,10名女生竞赛成绩的数据是随机的,所以µ1,µ2是随机的.
所以不能确定是否有µ1>µ2.
19.(1)在正四棱柱ABCD−A1B1C1D1中,连接BD交AC于N,连接MN.
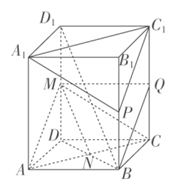
因为ABCD为正方形,所以N为BD中点,
在△DBD1中,因为M为DD1中点,所以BD1∥MN.
因为MN⊂平面AMC,BD1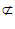 平面AMC,
平面AMC,
所以BD1∥平面AMC.
(2)因为ABCD为正方形,所以AC⊥BD.
因为DD1⊥平面ABCD,所以DD1⊥AC.
因为DD1∩BD=D,所以AC⊥平面BDD1.
因为BD1⊂平面BDD1,所以AC⊥BD1.
(3)当λ=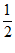 ,即点P为线段BB1的中点时,平面A1PC1∥平面AMC.
,即点P为线段BB1的中点时,平面A1PC1∥平面AMC.
因为AA1∥CC1,且AA1=CC1,
所以四边形AA1C1C是平行四边形,所以AC∥A1C1.
取CC1的中点Q,连接MQ,QB.
因为M为DD1中点,所以MQ∥AB,且MQ=AB,
所以四边形ABQM是平行四边形.所以BQ∥AM.
同理BQ∥C1P.
所以AM∥C1P.
因为A1C1∩C1P=C1,AC∩AM=A,
所以平面A1PC1∥平面AMC.
20.略.
