本试卷共三道大题，25道小题，满分100分。考试时间120分钟。
一、选择题（本题共24分，每小题3分）
第1~8题均有四个选项，符合题意的选项只有一个．
1．在抛物线y=x2-4x-5上的一个点的坐标为
A．(0,-4) B．(2,0) C．(1,0) D．(-1,0)
2．在半径为6cm的圆中，60°的圆心角所对弧的弧长是
A．πcm B．2πcm C．3πcm D．6πcm
3．将抛物线y=x2先向右平移3个单位长度，再向上平移5个单位长度，所得抛物线的解析式为
A．y=(x+3)2+5 B．y=(x-3)2+5 C．y=(x+5)2+3 D．y=(x-5)2+3
4．2020年是紫禁城建成600年暨故宫博物院成立95周年，在此之前有多个国家曾发行过紫禁城元素的邮品．图1所示的摩纳哥发行的小型张中的图案，以敞开的紫禁城大门和大门内的石狮和太和殿作为邮票和小型张的边饰，如果标记出图1中大门的门框并画出相关的几何图形（图2），我们发现设计师巧妙地使用了数学元素（忽略误差），图2中的四边形ABCD与四边形A’B’C’D’，是位似图形，点O是位似中心，点A’是线段OA的中点，那么以下结论正确的是：
A．四边形ABCD与四边形A’B’C’D’的相似比为1:1
B．四边形ABCD与四边形A’B’C’D’的相似比为1:2
C．四边形ABCD与四边形A’B’C’D’的周长比为3:1
D．四边形ABCD与四边形A’B’C’D’的面积比为4:1
5．如图，AB是⊙O的直径，CD是弦，若∠CDB=32°，则∠ABC等于
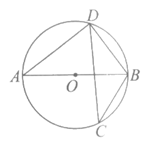
A．68° B．64°
C．58° D．32°
6．若抛物线y=ax2+bx+c(a≠0)经过A(1，0)，B(3，0)两点，则抛物线的对称轴为
A．x=1 B．x=2 C．x=3 D．x=4
7．近年来我国无人机产业迅猛发展，无人机驾驶员已正式成为国家认可的新职业．中国民用航空局的现有统计数据显示，从2017年底至2019年底，全国拥有民航局颁发的民用无人机驾驶执照的人数已由约2.44万人增加到约6.72万人．若设2017年底至2019年底，全国拥有民用无人机驾驶执照人数的年平均增长率为x，则可列出关于x的方程为
A．2.44 (1+x)= 6.72 B．2.44 (1+2x) =6.72
C．2.44 (1+x)2 =6.72 D．2.44 (1-x)2=6.72
8．现有函数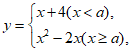
，如果对于任意的实数n，都存在实数m，使得当x=m时，y=n，那么实数a的取值范围是
A．-5≤a≤4 B．-1≤a≤4 C．-4≤a≤1 D．-4≤a≤5
二、填空题（本题共24分，每小题3分）
9．若正六边形的边长为2，则它的半径为________．
10．若抛物线y=ax2（a≠0）经过A(1，3)，则该抛物线的解析式为________．
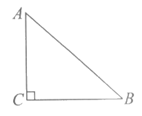
11．如图，在Rt△ABC中，∠C=90°，AC=6，AB=9，则sinB=________．
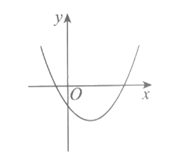
12．若抛物线y=ax2+bx+c（a≠0）的示意图如图所示，则a________0，b____0，c____0（填“>”，“=”或“<“）．
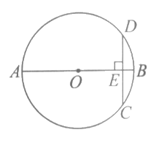
13．如图，AB为⊙O的直径，AB=10，CD是弦，AB⊥CD于点E，若CD=6，则EB=________．
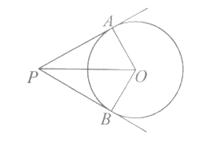
14．如图，PA，PB是⊙O的两条切线，A，B为切点，若OA=2，∠APB=60°，则PB=________．
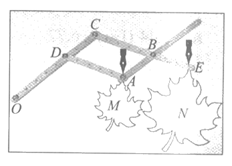
15．放缩尺是一种绘图工具，它能把图形放大或缩小．
制作：把钻有若干等距小孔的四根直尺用螺栓分别在点A，B，C，D处连接起米，使得直尺可以绕着这些点转动，O为固定点，OD=DA=CB，DC=AB=BE，在点A，E处分别装上画笔．
画图：现有一图形M，画图时固定点O，控制点A处的笔尖沿图形M的轮廓线移动，此时点E处的画笔便画出了将图形M放大后的图形N．
原理：
若连接OA，OE，可证得以下结论：
①△ODA和△OCE为等腰三角形，
则∠DOA=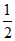
（180°-∠ODA），∠COE=
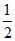（180°-∠________）；
②四边形ABCD为平行四边形（理由是________）；
③∠DOA=∠COE，于是可得O，A，E三点在一条直线上；
④当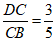
时，图形N是以点O为位似中心，把图形M放大为原来的________倍得到的．
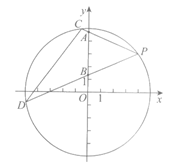
16．如图，在平面直角坐标系xOy中，P(4，3)，⊙O经过点P，点A，点B在y轴上，PA=PB，延长PA，PB分别交⊙O于点C，点D，设直线CD与x轴正方向所夹的锐角为α．
(1) ⊙O的半径为_______，
(2) tanα=_______．
三、解答题（本题共52分，第17、18、20～22题每小题5分，第19题6分，第23～25题每小题7分）
17．计算：2sin60°-tan45°+cos230°．
18．已知关于x的方程x2+2x+k-4=0．
(1)如果方程有两个不相等的实数根，求k的取值范围；
(2)若k=1，求该方程的根．
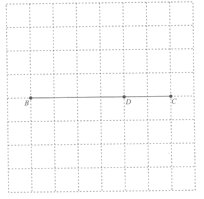
19．借助网格画图并说理：
如图所示的网格是正方形网格，△ABC的三个顶点是网格线的交点，点A在BC边的上方，AD⊥BC于点D，BD=4，CD=2，AD=3．以BC为直径作⊙O，射线DA交⊙O于点E，连接BE，CE．
(1)补全图形；
(2)填空：∠BEC=______°，理由是_______；
(3)判断点A与⊙O的位置关系并说明理由；
(4) ∠BAC_______∠BEC（填“>”，“=”或“<“）．
20．二次函数y=ax2+bx+c（a≠0）的图象经过(3，0)点，当x=1时，函数的最小值为-4．
(1)求该二次函数的解析式并画出它的图象；
(2)直线x=m与抛物线y=ax2+bx+c（a≠0）和直线y=x-3的交点分别为点C，点D，点C位于点D的上方，结合函数的图象直接写出m的取值范围．
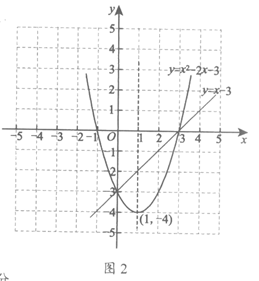
21．如图，AB为⊙O的直径，AC为弦，点D在⊙O外，∠BCD=∠A，OD交⊙O于点E．
(1)求证：CD是⊙O的切线；
(2)若CD=4，AC=2.7，cos∠BCD=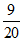
，求DE的长．
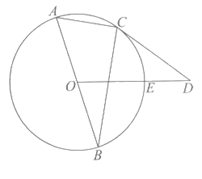
22．如图，正方形ABCD的边长为4，点E在AB边上，BE=1，F为BC边的中点．将正方形截去一个角后得到一个五边形AEFCD，点P在线段EF上运动（点P可与点E，点F重合），作矩形PMDN，其中M，N两点分别在CD，AD边上．设CM=x，矩形PMDN的面积为S．
(1)DM=_______（用含x的式子表示），x的取值范围是_______；
(2)求S与x的函数关系式；
(3)要使矩形PMDN的面积最大，点P应在何处？并求最大面积．
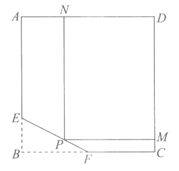
23．已知抛物线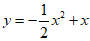
．
(1)直接写出该抛物线的对称轴，以及抛物线与y轴的交点坐标；
(2)已知该抛物线经过A(3n+4，y1)，B(2n-1，y2)两点．
①若n<-5，判断y1与y2的大小关系并说明理由;
②若A，B两点在抛物线的对称轴两侧，且y1>y2，直接写出n的取值范围．
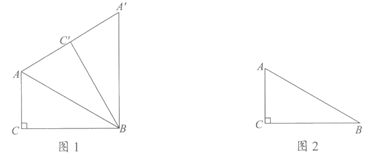
24．在Rt△ABC中，∠ACB=90°，∠ABC=30°，，BC=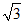
，将△ABC绕点B顺时针旋转α(0°<α≤120°)得到△A’BC’，点A，点C旋转后的对应点分别为点A’，点C’．
(1)如图1，当点C’恰好为线段AA’的中点时，α=____°，AA’=____；
(2)当线段AA’与线段CC’有交点时，记交点为点D．
①在图2中补全图形，猜想线段AD与A’D的数量关系并加以证明；
②连接BD，请直接写出BD的长的取值范围．
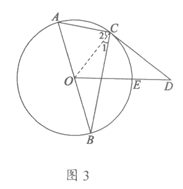
25．对于平面内的图形G1和图形G2，记平面内一点P到图形G1上各点的最短距离为d1，点P到图形G2上各点的最短距离为d2，若d1=d2，就称点P是图形G1和图形G2的一个“等距点“．在平面直角坐标系xOy中，已知点A(6，0)，B(0，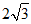
)．
(1)在R(3，0)，S(2，0)，T(1，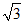
)三点中，点A和点B的等距点是_______；
(2)已知直线y=-2．
①若点A和直线y=-2的等距点在x轴上，则该等距点的坐标为_______；
②若直线y=a上存在点A和直线y=-2的等距点，求实数a的取值范围；
(3)记直线AB为直线l1，直线l2：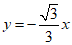
，以原点O为圆心作半径为r的⊙O．若⊙O上有m个直线l1和直线l2的等距点，以及n个直线l1和y轴的等距点(m≠0，n≠0)，当m≠n时，求r的取值范围.
参考答案
一、选择题（本题共24分，每小题3分）
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | D | B | B | D | C | B | C | A |
二、填空题（本题共24分，每小题3分）
9．2． 10．y=3x2．11．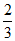
． 12．>,<,<． 13．1． 14．
．
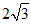15．OCE；两组对边分别相等的四边形是平行四边形；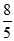
．
16．(1)5（1分）；(2)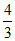 
（2分）．
三、解答题（本题共52分，第17、18、20～22题每小题5分，第19题6分，第23～25题每小题7分）
17．解：2sin60°-tan45°+cos230°
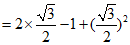…………………3分
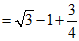
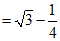.………………………………5分
18．解：(1)△=22-4×1×(k-4)…………………………1分
=20-4k．
∵方程有两个不相等的实数根，
∴△>0．……………………………2分
解得k<5．………………………………3分
(2)当k=1时，原方程化为x2+2x-3=0．
解得x1=-3，x2=1, ………………………………5分
19．解：(1)补全图形见图1．……………………………1分
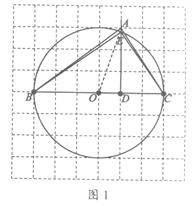
(2) 90，直径所对的圆周角是直角 ………………………………3分
(3)点A在⊙O外，
理由如下：连接OA．
∵BD=4，CD=2,
∴BC=BD+CD=6,
．
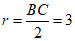∵AD⊥BC,
∴∠ODA=90°．
在Rt△AOD中，AD=3, OD=BD-OB=1，
∴
∵
,
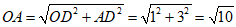
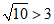∴OA>r．……………………………………4分
∴点A在⊙O外．……………………………………5分
(4)∠BAC<∠BEC．…………………………………………6分
20．解：(1)∵当x=1时，二次函数y=ax2+bx+c
（a≠0）的最小值为-4，
∴二次函数的图象的顶点为(1，-4)．
∴二次函数的解析式可设为
y=a(x-1)2-4（a≠0）．
∵二次函数的图象经过(3，0)点，
∴a（3-1）2-4=0．
解得a=1．
∴该二次函数的解析式为
y=(x-1)2-4．……………………………2分
画图象见图2．……………………………………3分
(2)m<0或m>3．………………………………………5分
21．(1)证明：如图3，连接OC．
∵AB为⊙O的直径，AC为弦，
∴∠ACB=90°，∠1+∠2=90°．
∵OA=OC，
∴∠2=∠A．
∵∠BCD=∠A,
∴∠2=∠BCD．
∴∠1+∠BCD=90°．
∴∠OCD=90°．
∴CD⊥OC．………………………………………………2分
∵OC为⊙O的半径，
∴CD是⊙O的切线．…………………………………3分
(2)解：∵∠BCD=∠A, cos∠BCD=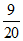
，
∴cosA=cos∠BCD=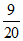
．
在Rt△ABC中，∠ACB=90°，AC=2.7, cosA=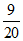
，
∴
.
∴
.
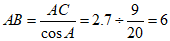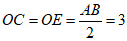在Rt△OCD中，∠OCD=90°，OC=3, CD=4,
∴
.
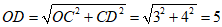∴DE=OD-OE=5-3=2．…………………………………………5分
22．解：如图4．
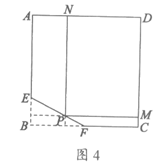
(1) 4-x，0≤x≤1．…………………………………2分
(2)可得DN=PM=2x+2．
S=DM·DN=(4-x)(2x+2)=-2x2+6x+8,
其中0≤x≤1．…………………………3分
(3)∵此抛物线开口向下，对称轴为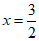
，
∴当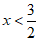
时，y随x的增大而增大．
∵x的取值范围为0≤x≤1，
∴当x=1时，矩形PMDN的面积最大，此时点P与点E重合，此时最大面积为12．…………………5分
23．解：(1)x=1，(0，0)．…………………………………2分
(2) xA-xB=（3n+4）–（2n-1）=n+5，
xA-1= (3n+4)-1=3n+3=3(n+1),
xB-1=（2n-1）-1=2n-2=2（n-1）．
①当n< -5时，xA-1<0，xB-1<0，xA-xB<0．
∴A，B两点都在抛物线的对称轴x=1的左侧，且xA<xB．…………4分
∵抛物线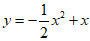
开口向下，
∴在抛物线的对称轴x=1的左侧，y随x的增大而增大．
∴y1<y2．……………………………5分
②-1<n<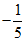
………………………………7分
24．解：(1) 60，2．…………………………………………2分
(2)①补全图形见图5．…………………………………3分
AD=A’D．
证明如下：
如图5，过点A作A’C’的平行线，交CC’于点E，记∠1=β，
∵将Rt△ABC绕点B顺时针旋转α得到Rt△A’BC’，
∴∠A’C’B=∠ACB=90°，A’C’=AC，BC’=BC．
∴∠2=∠1=β．
∴∠3=∠ACB-∠1=90°-β，∠A’C’D=∠A’C’B+∠2=90°+β．
∵AE∥A’C’，
∴∠AED=∠A’C’D=90°+β,
∴∠4=180°-∠AED=180°- (90°+β) =90°-β．
∴∠3=∠4
∴AE=AC
∴AE=A’C’．
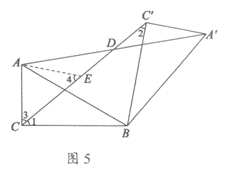
在△ADE和△A’DC’中，
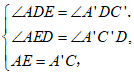
∴△ADE≌△A’DC’．……………………………………4分
∴AD=A’D．……………………………………5分
证法不唯一．
②1≤BD≤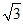 
．…………………………………………………………7分
25．解：(1)S(2，0)．…………………………………1分
(2)①(4，0)或(8，0)．……………………………………3分
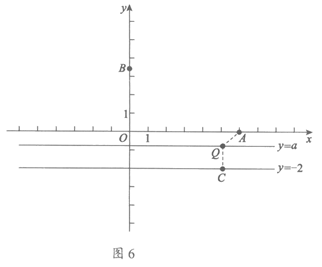
②如图6，设直线y=a上的点Q为点A和直线y=-2的等距点，连接QA，过点Q作直线y=-2的垂线，垂足为点C．
∵点Q为点A和直线y=-2的等距点，
∴QA=QC．
∴QA2=QC2．
∵点Q在直线y=a上，
∴可设点Q的坐标为Q(x，a)．
∴（x-6）2+a2=[a-（-2）]2．
整理得x2-12x+32-4a=0．
由题意得
关于x的方程x2-12x+32-4a=0有实数根．
∴△=(-12)2-4×1×(32-4a)=16(a+l)≥0．
解得a≥-1．…………………………………………5分
(3)如图7．
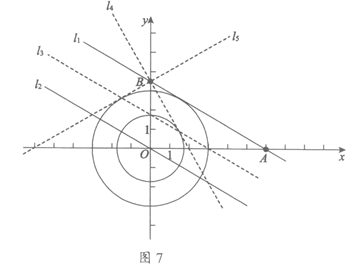
直线l1和直线l2的等距点在直线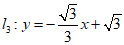
上．
直线l1和y轴的等距点在直线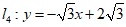
或
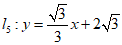上．
由题意得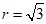
或r≥3．……………………………7分