本试卷共150分。考试时长120分钟。
第一部分（选择题
共40分）
一、选择题共10小题，每小题4分，共40分。在每小题列出的四个选项中，选出符合题目要求的一项。
(1)已知集合A={-1，0，2，3），B={x|x=2k-1，k∈N}，那么A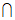
B=
(A){-1，0） (B){-1，2） (C){0，3} (D){-1，3}
（2）方程组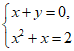
的解集是
(A){(1,-1),(-1,1)} (B){(1,1),(-2,2)}
(C){(1,-1),(-2,2) } (D){(2，-2),(-2,2) }
(3)函数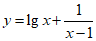
的定义域是
(A)(0,+∞) (B)(1,+∞) (C)(0,1)U(1,+∞) (D)[0,1)U(1,+∞)
(4)为了解学生在“弘扬传统文化，品读经典文学“月的阅读情况，现从全校学生中随机抽取了部分学生，并统计了他们的阅读时间（阅读时间t∈[0，50]），分组整理数据得到如图所示的频率分布直方图．则图中a的值为
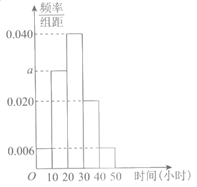
(A) 0.028
(B) 0.030
(C) 0.280
(D) 0.300
(5)若a>b，则一定有
(A)
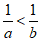(B)
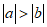(C)
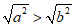(D) a3> b3
(6)在平行四边形ABCD中，设对角线AC与BD相交于点O，则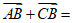
(A) 2
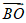
(B) 2
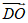
(C)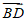 
(D)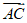
(7)设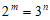
，则m，n的大小关系一定是
(A)m>n (B)m<n (C)m≥n (D)以上答案都不对
(8)从2015年到2020年，某企业通过持续的技术革新来降低其能源消耗，到了2020年该企业单位生产总值能耗降低了20%．如果这五年平均每年降低的百分率为x，那么x满足的方程是
(A) 5x=0.2 (B) 5(1-x)=0.8 (C) x5=0.2 (D) (1-x)5=0.8
(9)设a，b为平面向量，则“存在实数λ(λ≥0)，使得a=λb“是“|a+ b|=|a|+|b|”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(10)设f(x)为定义在R上的函数，函数f(x+1）是奇函数，对于下列四个结论：
①f(1)=0；
②f (1-x)=-f(1+x)；
③函数f(x)的图像关于原点对称；
④函数f(x)的图像关于点(1，0)对称；
其中，正确结论的个数为
(A)1 (B)2 (C)3 (D)4
第二部分（非选择题
共110分）
二、填空题共5小题，每小题5分，共25分。
(11)已知向量a=(1，-2)，b=(-3，1)，那么|a–b|=__________．
(12)若方程x2 -2x+a =0有两个不相等的正实数根，则实数a的取值范围是_________．
(13)设f(x)为R上的奇函数，且f(x)在(0，+∞)上单调递增，f(2)=0，则不等式f(x)<0的解集是_________．
(14)已知函数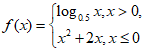
那么f(2)=_________；当函数y=f(x)-a有且仅有三个零点时，实数a的取值范围是_________．
(15)某厂商为推销自己品牌的可乐，承诺在促销期内，可以用3个该品牌的可乐空罐换1罐可乐．对于此促销活动，有以下三个说法：
①如果购买10罐可乐，那么实际最多可以饮13罐可乐；
②欲饮用100罐可乐，至少需要购买67罐可乐；
③如果购买n(n∈N*)罐可乐，那么实际最多可饮用可乐的罐数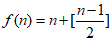
。（其中[x]表示不大于x的最大整数）
则所有正确说法的序号是_________．
三、解答题共6小题，共85分。解答应写出文字说明，演算步骤或证明过程。
(16)（本小题13分）
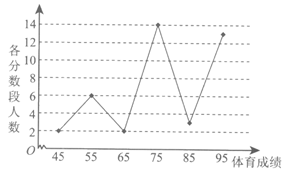
某校高一年级1000名学生全部参加了体育达标测试，现从中随机抽取40名学生的测试成绩，整理并按分数段[40，50)，[50，60)，[60，70)，[70，80)，[80，90)，[90，100]进行分组，假设同一组中的每个数据可用该组区间的中点值代替，则得到体育成绩的折线图如下．
(I)估计该校高一年级中体育成绩大于或等于70分的学生人数；
(II)现从体育成绩在[60，70)和[80，90)的样本学生中随机抽取2人，求其中恰有1人体育成绩在[60，70)的概率．
(17)（本小题15分）
设函数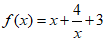
.
(I)求函数f(x)的图像与直线y=2x交点的坐标；
(II)当x∈(0，+∞)时，求函数f(x)的最小值；
(III)用单调性定义证明：函数f (x)在(2，+∞)上单调递增．
(18)（本小题14分）
以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩，乙组记录中有一个数字模糊，无法确认，假设这个数字具有随机性，并在图中以a表示．
(I)若甲、乙两组的数学平均成绩相同，求a的值；
(II)求乙组平均成绩超过甲组平均成绩的概率;
(III)当a=3时，试比较甲、乙两组同学数学成绩的方差的大小．（结论不要求证明）
(19)（本小题15分）
设函数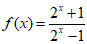
．
(I)若f（a）=2，求实数a的值；
(II)判断函数f(x)的奇偶性，并证明你的结论；
(III)若f(x)≤m对于x∈[1，+∞)恒成立，求实数m的最小值．
(20)（本小题13分）
经销商经销某种农产品，在一个销售季度内，每售出1吨该产品获利润500元，未售出的产品，每1吨亏损300元，经销商为下一个销售季度购进了130吨该农产品，以x（单位：吨，100≤x≤150）表示下一个销售季度内的市场需求量，y（单位：元）表示下一个销售季度内销售该农产品的利润．
(I)将y表示为x的函数；
(II)求出下一个销售季度利润y不少于57000元时，市场需求量x的范围．
(21)（本小题15分）
设函数f(x)的定义域为R．若存在常数m(m≠0)，对于任意x∈R，f（x+m）=mf(x)成立，则称函数f(x)具有性质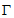
，记P为满足性质
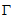的所有函数的集合．
(I)判断函数y=x和y=2是否属于集合P?（结论不要求证明）
(II)若函数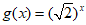
，证明：g(x)∈P；
(III)记二次函数的全体为集合Q，证明：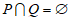
．
参考答案
一、选择题：本大题共10小题，每小题4分，共40分．
1． D 2． C 3． C 4． A 5． D
6． B 7． D 8． D 9． A 10．C
二、填空题：本大题共5题，每小题5分，共25分．
11．5 12．(0，1) 13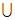．(-∞，-2)
(0，2)
14． -1; (-1，0] 15．②③
注：第14题第一问2分，第二问3分；第15题全部选对得5分，不选或有错选得0分，其他得3分，
三、解答题：本大题共6小题，共85分，其他正确解答过程，请参照评分标准给分．
16．（本小题13分）
解：(I)由折线图，知样本中体育成绩大于或等于70分的学生有30人， ………………2分
所以该校高一年级学生中体育成绩大于或等于70分的学生约有1000×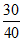
= 750人．
……………………………5分
(II)设“其中恰有1人体育成绩在[60，70)”为事件M， ………………………6分
记体育成绩在[60，70)的数据为A1，A2，体育成绩在[80，90)的数据为B1，B2，B3，
则从这两组数据中随机抽取2个，所有可能的结果有10种，它们是：(A1，A2)，(A1,B1)，
(A1，B2)，(A1，B3)，(A2，B1)，（A2，B2），(A2，B3)，(B1，B2)，(B1，B3)，（B2，B3）．…………8分
而事件M的结果有6种，它们是：(A1，B1)，(A1，B2)，(A1，B3)，（A2，B1），（A2，B2），(A2，B3)， ………………………………………………10分
因此事件M的概率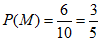
． ………………………………13分
17．（本小题15分）
解：( I)由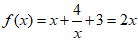
，解得x1=-1，x2=4． …………………………2分
所以函数f(x)的图像与直线y=2x的交点为(-1，-2)，(4，8)． ………………4分
(II)因为x>0，
所以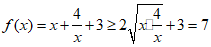
……………………7分
当且仅当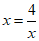
，即x=2时取等号．
故当x=2时，函数f(x)在(0，+∞)上取到最小值7． …………………………9分
(III)任取x1，x2∈(2，+∞)，且x1<x2，那么
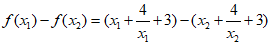………11分
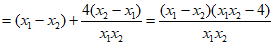………13分
因为2<x1<x2，
所以x1-x2<0，x1x2-4>0，
从而f(x1)-f(x2) <0，即f(x1)<f(x2)．
所以函数f (x)在(2，+∞)上单调递增， ………15分
18．（本小题14分）
解：(I)依题意，得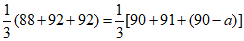
…………………………3分
解得a=1． ……………………………………………………4分
(II)设“乙组平均成绩超过甲组平均成绩“为事件A， …………5分
依题意a=0，1，2，…，9．共有10种可能， ………7分
由(I)，知当a=1时甲、乙两个小组的数学平均成绩相同，
故当a=2，3，4，…，9时，乙组平均成绩超过甲组平均成绩，共有8种可能．…9分
所以乙组平均成绩超过甲组平均成绩的概率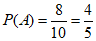
． ………………11分
(III)甲组同学数学成绩的方差大于乙组同学数学成绩的方差． …………14分
19．（本小题15分）
解：(I)由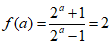
，解得2a =3． ………2分
所以a=log2 3． ………4分
(II)结论：函数f(x)为奇函数． ………5分
证明如下：
函数f(x)的定义域为（-∞，0）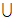
（0，+∞）． ………6分
因为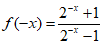
………7分
,
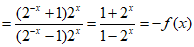所以函数f(x)为奇函数， ………9分
(III)
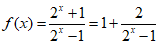……11分
由x∈[1，+∞)，得2x≥2，即2x-1≥1．
故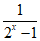
∈（0,1]，则
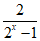∈（0,2]．
所以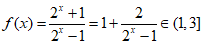
.
即f(x)的值域为(1，3]． ……………………………………13分
由f(x)≤m对于x∈[1，+∞)恒成立，得m≥3，
所以实数m的最小值为3． …………………………………………15分
20．（本小题13分）
解：(I)当x∈[100，130)时，y=500x-300(130-x)=800x-39000；………………3分
当x∈[130，150]时，y=500×130= 65000． ………6分
所以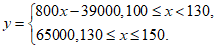
……8分
( II)由y≥57000，解得x∈[120，150]．
故下一个销售季度利润y不少于57000元时，市场需求量x∈[120，150]．……13分
21．（本小题15分）
解：(I)函数y=x不属于集合P；函数y=2属于集合P． ……3分
( II)证明：设m=2， ……………………………………6分
因为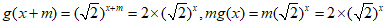
，
所以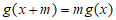
．
故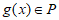
…………………………9分
（注：本小问中的m还可以等于4）
(III)设二次函数f(x)=ax2+ bx+ c(a≠0)为集合Q中的任意一个元素，………10分
假设存在常数m(m≠0)，对于任意x∈R，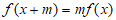
成立，……11分
因为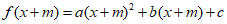
，
，
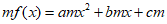所以ax2+ (2ma+b)x+ (am2+bm+c)=amx2+bmx+cm对于任意x∈R成立．
……13分
所以a=am①；2ma+b=bm ②；am2+ bm+c=cm③同时成立．
由①及a≠0，得m=1．
代入②，得a=0，这与a≠0矛盾，
所以不存在常数m(m≠0)，对于任意x∈R，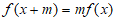
成立，
所以
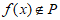，即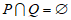
． ……………………15分