本试卷共四道大题,26道小题。满分100分。考试时间100分钟。
一、选择题(本题共20分,每小题2分)
第1—10题均有四个选项,符合题意的选项只有一个。
1. 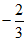 的相反数是
的相反数是
A. 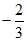 B.
B. 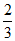 C.
C. 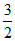 D.
D.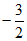
2. 国家统计局公布的数据显示,经初步核算,2020年尽管受到新冠疫情的影响,前三个季度国内生产总值仍然达到近697 800亿元,按可比价格计算,同比增长了6.2%,将数据697 800用科学记数法表示为
A. 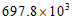 B.
B. 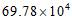 C.
C. 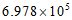 D.
D.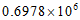
3. 下列计算正确的是
A. 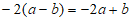 B.
B.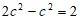
C. 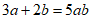 D.
D.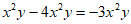
4. 下图是某个几何体的平面展开图,则这个几何体是
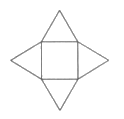
A. 长方体 B. 三棱柱 C. 四棱锥 D. 三棱锥
5. 下列方程变形中,正确的是
A. 方程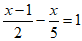 ,去分母得
,去分母得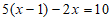 ;
;
B. 方程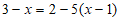 ,去括号得
,去括号得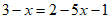 ;
;
C. 方程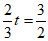 ,系数化为1得
,系数化为1得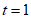 ;
;
D. 方程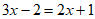 ,移项得
,移项得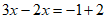 。
。
6. 如图,OA表示北偏东20°方向的一条射线,OB表示南偏西50°方向的一条射线,则∠AOB的度数是
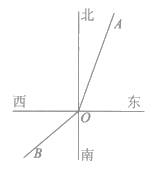
A. 100° B. 120° C. 140° D. 150°
7. 若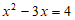 ,则
,则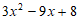 的值是
的值是
A. 20 B. 16 C. 4 D. -4
8. 如图,数轴上的点A表示的数为有理数a,下列各数中在0,1之间的是
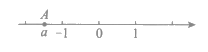
A. 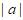 B.
B. 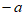 C.
C. 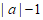 D.
D.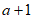
9. 下列说法正确的是
(1)如果互余的两个角的度数之比为1:3,那么这两个角分别为45°和135°
(2)如果两个角是同一个角的补角,那么这两个角不一定相等
(3)如果两个角的度数分别是73°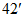 和16°
和16°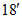 ,那么这两个角互余
,那么这两个角互余
(4)一个锐角的余角比这个锐角的补角小90°
A. 1个 B. 2个 C. 3个 D. 4个
10. 如图表示3×3的数表,数表每个位置所对应的数都是1,2或3,定义a*b为数表中第a行第b列的数。例如,数表第3行第1列所对应的数是2,所以3*1=2。

A. 0,2 B. 1,2 C. 1,0 D. 1,3
二、填空题(本题共16分,每小题2分)
11. 用四舍五入法取近似数:2.7682≈__________(精确到0.01)。
12. 若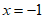 是关于x的方程
是关于x的方程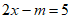 的解,则m的值是__________。
的解,则m的值是__________。
13. 若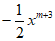
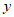 与
与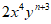 是同类项,则
是同类项,则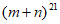 =___________。
=___________。
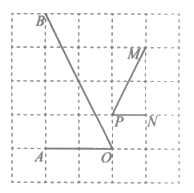
14. 如图所示的网格是正方形网格,则∠AOB__________∠MPN。(填”>”,”=”或”<“)
15. 用符号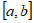 表示
表示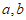 两数中的较大者,用符号
两数中的较大者,用符号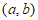 表示
表示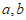 两数中的较小者,则
两数中的较小者,则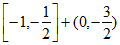 的值为_____________。
的值为_____________。
16. 我国古代数学著作《孙子算经》中记载了这样一个有趣的数学问题”今有五等诸侯,共分橘子60颗,人别加三颗,问五人各得几何?”题目大意是:诸侯五人,共同分60个橘子,若后面的每个人总比他前一个人多分3个,问每个人各分得多少个橘子?若设中间的那个人分得x个橘子,依题意可列方程为_____________。
17. 如图,C,D,E为线段AB上三点,
(1)若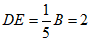 ,则AB的长为___________;
,则AB的长为___________;
(2)在(1)的条件下,若点E是DB的中点,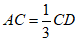 ,则CD的长为_______。
,则CD的长为_______。

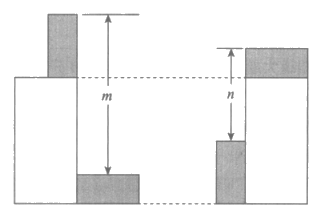
18. 有四个大小完全相同的小长方形和两个大小完全相同的大长方形按如图所示的位置摆放,按照图中所示尺寸,小长方形的长与宽的差是__________。(用含m,n的式子表示)
三、解答题(本题共45分,第20题20分,第22题10分,其余每题5分)
19. 如图,已知平面内有四个点A,B,C,D。
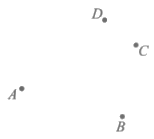
根据下列语句按要求画图。
(1)连接AB;
(2)作射线AD,并在线段AD的延长线上用圆规截取DE=AB;
(3)作直线BC与射线AD交于点F。
观察图形发现,线段AF+BF>AB,得出这个结论的依据是:_______________________。
20. 计算:
(1)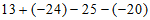 ;
;
(2)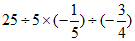 ;
;
(3)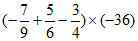 ;
;
(4)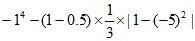 。
。
21. 先化简,再求值: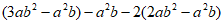 ,其中
,其中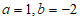 。
。
22. 解下列方程:
(1)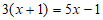 ;
;
(2)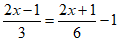 。
。
23. 解方程组: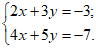
四、解答题(本题共19分,第24题5分,第25题6分,第26题8分)
24. 请补全下面的解题过程(括号中填写推理的依据)。
已知:如图,点A,O,B在同一条直线上,OD平分∠AOE,∠COD=90°。
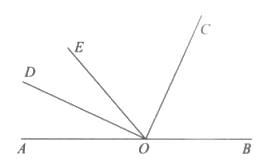
求证:OC是∠BOE的平分线。
证明:因为OD是∠AOE的平分线,
所以∠AOD=∠DOE。
(理由:_____________________)
因为∠COD=90°,
所以∠DOE+∠__________=90°,
∠AOD+∠BOC=180°-∠COD=__________°。
因为∠AOD=∠DOE,
所以∠__________=∠___________。
(理由:___________________)
所以OC是∠BOE的平分线。
25. 某环卫公司通过政府采购的方式计划购进一批A,B两种型号的新能源汽车。据了解,2辆A型汽车和3辆B型汽车的进价共计80万元;3辆A型汽车和2辆B型汽车的进价共计95万元。
(1)求A,B两种型号的汽车每辆进价分别为多少万元;
(2)该公司计划恰好用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),并使得购进的B种型号的新能源汽车数量多于A种型号的新能源汽车数量,请直接写出该公司的采购方案。
26. 数轴上有A,B两个点,点A在点B的左侧,已知点B表示的数是2,点A表示的数是a。
(1)若a=-3,则线段AB的长为____________;(直接写出结果)
(2)若点C在线段AB之间,且AC-BC=2,求点C表示的数;(用含a的式子表示)
(3)在(2)的条件下,点D在数轴上C点左侧,AC=2AD,BD=4BC,求a的值。
附加题
试卷满分:20分
一、填空题(本题6分)
1. 观察下列等式,探究其中的规律并回答问题:
1+8=32,
1+8+16=52,
1+8+16+24=72,
1+8+16+24+32=k2,
…,…
(1)第4个等式中正整数k的值是_____________;
(2)第5个等式是:______________________;
(3)第n个等式是:________________________。(其中n是正整数)
二、解答题(本题共14分,第2题6分,第3题8分)
2. 下图所示的三种拼块A,B,C,每个拼块都是由一些大小相同、面积为1个单位的小正方形组成,如编号为A的拼块的面积为3个单位。
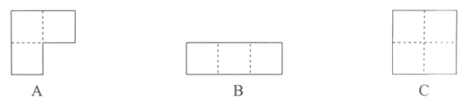
现用若干个这三种拼块拼正方形,拼图时每种拼块都要用到,且这三种拼块拼图时可平移、旋转,或翻转。
(1)若用1个A种拼块,2个B种拼块,4个C种拼块,则拼出的正方形的面积为___________个单位;
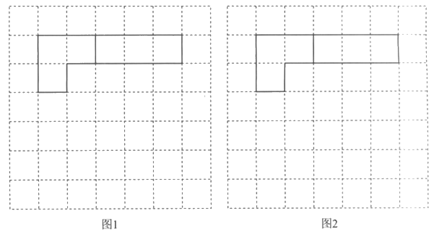
(2)在图1和图2中,各画出了一个正方形拼图中1个A种拼块和1个B种拼块,请分别用不同的拼法将图1和图2中的正方形拼图补充完整。要求:所用的A,B,C三种拼块的个数与(1)不同,用实线画出边界线,拼块之间无缝隙,且不重叠。
3. 对于数轴上的点A,B,C,D,点M,N分别是线段AB,CD的中点,若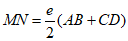 ,则将e的值称为线段AB,CD的相对离散度。特别地,当点M,N重合时,规定
,则将e的值称为线段AB,CD的相对离散度。特别地,当点M,N重合时,规定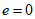 。设数轴上点O表示的数为0,点T表示的数为2。
。设数轴上点O表示的数为0,点T表示的数为2。
(1)若数轴上点E,F,G,H表示的数分别是-3,-1,3,5,则线段EF,OT的相对离散度是___________,线段FG,EH的相对离散度是___________;
(2)设数轴上点O右侧的点S表示的数是s,若线段OS,OT的相对离散度为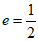 ,求s的值;
,求s的值;
(3)数轴上点P,Q都在点O的右侧(其中点P,Q不重合),点R是线段PQ的中点,设线段OP,OT的相对离散度为e1,线段OQ,OT的相对离散度为e2,当e1=e2时,直接写出点R所表示的数r的取值范围。
【试题答案】
一、选择题(本题共20分,每小题2分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | B | C | D | C | A | D | A | C | B | C |
二、填空题(本题共16分,每小题2分)
11. 2.77 12. -7 13. -1 14. =
15. -2 16. 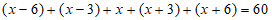 ,或
,或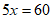
17. 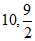 18.
18.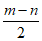
三、解答题(本题共45分,第20题20分,第22题10分,其余每题5分)
19. 解:
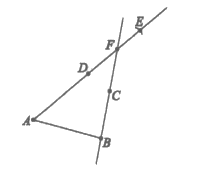
线段AF+BF>AB,依据:两点之间,线段最短。 5分
20. 解:(1)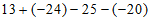
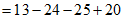 2分
2分
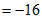 。 5分
。 5分
(2)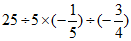
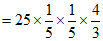 3分
3分
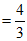 。 5分
。 5分
(3)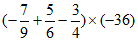
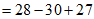 3分
3分
=25。 5分
(4)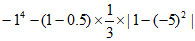
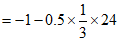 3分
3分
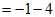
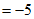 。 5分
。 5分
21. 解: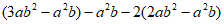
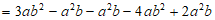
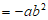 。 3分
。 3分
当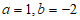 时,
时,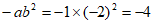 。 5分
。 5分
22. 解:(1)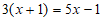 。
。
去括号,得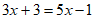 ,
,
移项,得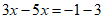 , 3分
, 3分
合并同类项,得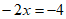 ,
,
系数化1,得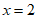 。 5分
。 5分
(2)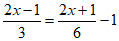 。
。
去分母,得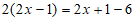 ,
,
去括号,得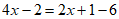 ,
,
移项,得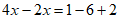 ,
,
合并同类项,得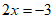 ,
,
系数化1,得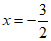 。 5分
。 5分
23. 解: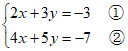
①×2,得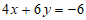 。
。
③
②-③,得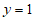 。
。
将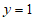 代入①,得
代入①,得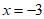 ,
,
所以,这个方程组的解是
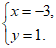
四、解答题(本题共19分,第24题5分,第25题6分,第26题8分)
24. 证明:因为OD是∠AOE的平分线,
所以∠AOD=∠DOE。
(理由:角平分线的定义)
因为∠COD=90°,
所以∠DOE+∠COE=90°,
∠AOD+∠BOC=180°-∠COD=90°。
因为∠AOD=∠DOE,
所以∠COE=∠BOC。
(理由:等角的余角相等)
所以OC是∠BOE的平分线。
25. 解:(1)设A,B两种型号的汽车每辆进价分别为x万元,y万元。
依题意,列出的方程组为
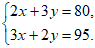
解这个方程组,得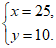
答:A,B两种型号的汽车每辆进价分别为25万元,10万元。
(2)购进A型号的新能源汽车2台,B型号的新能源汽车15台;
购进A型号的新能源汽车4台,B型号的新能源汽车10台。
26. 解:(1)5; 1分
(2)设C点表示的数为x,则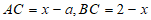 ,
,
因为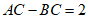 ,
,
所以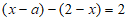 , 2分
, 2分
解这个方程,得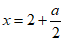 , 3分
, 3分
所以C点表示的数为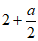 。 4分
。 4分
(3)依题意,得
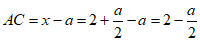 ,
,
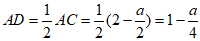
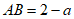 。
。
当点D在点A的左侧时,
因为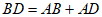 ,
,
所以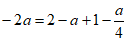 ,
,
解得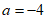 。 6分
。 6分
当点D在点A的右侧,点C的左侧时,
因为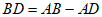 ,
,
所以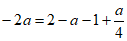 ,
,
解得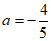 ,
,
综上,a的值为-4或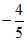 。 8分
。 8分
附加题答案:
一、填空题(本题6分)
1. (1)9; 2分
(2)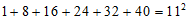 ; 4分
; 4分
(3)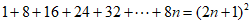 。 6分
。 6分
二、解答题(本题共14分,第2题6分,第3题8分)
2. 解:(1)25; 2分
(2)答案不唯一,如:
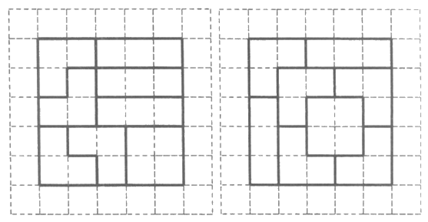
6分
3. 解:(1)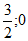 2分
2分
(2)设线段OS,OT的中点分别为L,K,
因为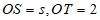 ,
,
所以点L,K在数轴上表示的数分别为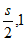 ,
,
所以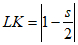 。 3分
。 3分
因为线段OS,OT的相对离散度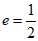 ,
,
所以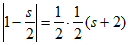 。(*) 4分
。(*) 4分
由题意,可知点L与点K不能重合,
所以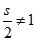 ,即
,即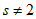 。
。
当点L在点K的左侧时,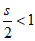 ,
,
(*)式化为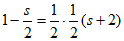 ,
,
解这个方程,得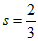 。 5分
。 5分
当点L在点K的右侧时,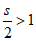 ,
,
(*)式化为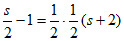 ,
,
解这个方程,得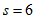 。
。
综上,s的值为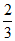 或6。 6分
或6。 6分
(3)数r的取值范围是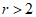 。 8分
。 8分
