本试卷共三道大题,26道小题。满分100分。考试时间100分钟。
一、选择题(本题共30分,每小题3分)
第1~l0题均有四个选项,符合题意的选项只有一个.
1.3-2的计算结果为
A.6 B.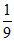 C.
C.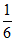 D.9
D.9
2.下列图形中,是轴对称图形的是
3.下列运算中正确的是
A.a2+a=a3 B.a5·a2=a10 C. (a2)3=a8 D.
(ab2)2=a2b4
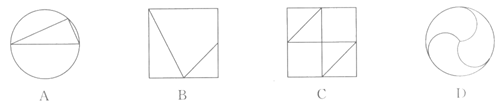
4.如图,在△ABC和△DEF中,∠C=∠F=90°,添加下列条件,不能判定这两个三角形全等的是
A.∠A=∠D,∠B=∠E B.AC=DF,AB=DE
C.∠A=∠D,AB=DE D.AC=DF,CB=FE
5.化简分式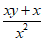 的结果是
的结果是
A.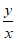 B.
B.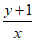 C.
C.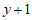 D.
D.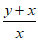
6.如果m2+m=5,那么代数式m(m-2)+(m+2)2的值为
A.14 B.9 C.-1 D.-6
7.已知一次函数y=kx-6,且y随x的增大而减小.下列四个点中,可能是该一次函数图象与x轴交点的是
A.(0,0) B.(2,0) C.(-2,0) D.(6,0)
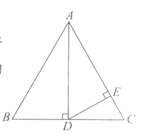
8.如图,在△ABC中,点D,E分别在边AB,BC上,点A与点E关于直线CD对称.若AB=7,AC=9,BC=12,则△DBE的周长为
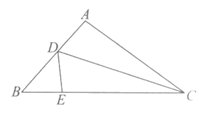
A.9 B.10
C.11 D.12
9.在学校组织的秋季登山活动中,某班分成甲、乙两个小组同时开始攀登一座450m高的山.乙组的攀登速度是甲组的1.2倍,乙组到达顶峰所用时间比甲组少15min.如果设甲组的攀登速度为x m/min,那么下面所列方程中正确的是
A.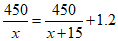 B.
B.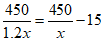
C.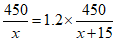 D.
D.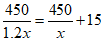
10.如图1,四边形ABCD是轴对称图形,对角线AC,BD所在直线都是其对称轴,且AC,BD相交于点E.动点P从四边形ABCD的某个顶点出发,沿图1中的线段匀速运动,设点P运动的时间为x,线段EP的长为y,图2是y与x的函数关系的大致图象,则点P的运动路径可能是
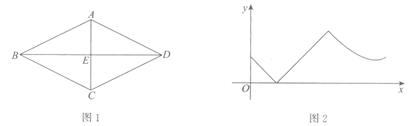
A.C→B→A→E B.C→D→E→A
C.A→E→C→B D.A→E→D→C
二、填空题(本题共18分,第15,17题每小题3分,其余每小题2分)
11.若分式
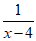
有意义,则x的取值范围是_________.
12.点A(1,-3)关于x轴对称的点的坐标为_________.
13.计算:10a2b3÷(-5ab3)=_________.
14.如图,△ABC≌△ADE,点D在边BC上,∠EAC=36°,则∠B=_________°.
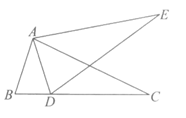
15.已知小腾家、食堂、图书馆在同一条直线上,小腾从家去食堂吃早餐,接着去图书馆查阅资料,然后回家.下面的图象反映了这个过程中小腾离家的距离y(单位:m)与时间x(单位:min)之间的对应关系.根据图象可知,小腾从食堂到图书馆所用时间为_________min;请你根据图象再写出一个结论:____________________________________。
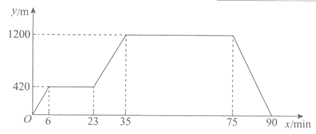
16.如图1,先将边长为a的大正方形纸片ABCD剪去一个边长为b的小正方形EBGF,然后沿直线EF将纸片剪开,再将所得的两个长方形按如图2所示的方式拼接(无缝隙,无重叠),得到一个大的长方形AEGC.根据图1和图2的面积关系写出一个等式:__________________.(用含a,b的式子表示)
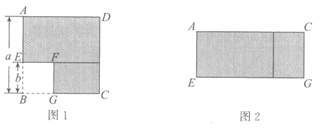
17.如图,△ABC是等边三角形,AD⊥BC于点D,DE⊥AC于点E.若AD=12,则DE=_________;△EDC与△ABC的面积关系是: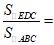 _________.
_________.
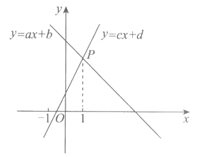
18.如图,一次函数y=ax+b与y=cx+d的图象交于点P.
下列结论中,所有正确结论的序号是_________.
①b<0;②ac<0;③当x>1时,ax+b>cx+d;
④a+b=c+d;⑤c>d,
三、解答题(本题共52分,第19题8分,第20~24题每小题6分,第25,26题每小题7分)
19.分解因式:
(1)x3-25x; (2)m(a-3)+2(3-a).
20.计算: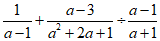 .
.
21.小红发现,任意一个直角三角形都可以分割成两个等腰三角形.
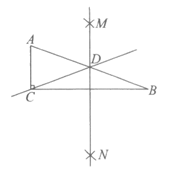
已知:在△ABC中,∠ACB=90°.
求作:直线CD,使得直线CD将△ABC分割成两个等腰三角形.
下面是小红设计的尺规作图过程.
作法:如图,
①作直角边CB的垂直平分线MN,与斜边AB相交于点D;
②作直线CD.
所以直线CD就是所求作的直线.
根据小红设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明,
证明:∵直线MN是线段CB的垂直平分线,点D在直线MN上,
∴DC=DB.(__________________)(填推理的依据)
∴∠_____________=∠_____________.
∵∠ACB=90°,
∴∠ACD=90°-∠DCB,
∠A=90°-∠_________.
∴∠ACD=∠A.
∴DC=DA.(__________________)(填推理的依据)
∴△DCB和△DCA都是等腰三角形.
22.解方程: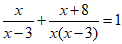 .
.
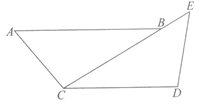
23.如图,AB∥CD,点E在CB的延长线上,∠A=∠E,AC=ED.
(1)求证:BC=CD;
(2)连接BD,求证:∠ABD=∠EBD.
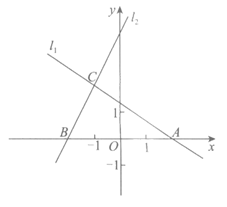
24.如图,在平面直角坐标系xOy中,直线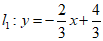 与x轴交于点A.
与x轴交于点A.
直线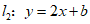 与x轴交于点B,且与直线l1交于点C(-1,m).
与x轴交于点B,且与直线l1交于点C(-1,m).
(1)求m和b的值;
(2)求△ABC的面积;
(3)若将直线l2向下平移t(t>0)个单位长度后,所得到的直线与直线l1的交点在第一象限,直接写出t的取值范围.
25.给出如下定义:在平面直角坐标系xOy中,已知点P1(a,b),P2((c,b),P3(c,d),这三个点中任意两点间的距离的最小值称为点P1,P2,P3的“最佳间距“.
例如:如图,点P1(-1,2),P2(1,2),P3(1,3)的“最佳间距“是1.
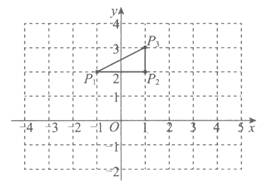
(1)点Q1(2,1),Q2(4,1),Q3(4,4)的“最佳间距“是_________,
(2)已知点O(0,0),A(-3,0),B(-3,y).
①若点O,A,B的“最佳间距“是1,则y的值为__________,
②点O,A,B的“最佳间距“的最大值为_____________;
(3)已知直线l与坐标轴分别交于点C(0,3)和D(4,0),点P(m,n)是线段CD上的一个动点.当点O(0,0),E(m,0),P(m,n)的“最佳间距“取到最大值时,求此时点P的坐标.
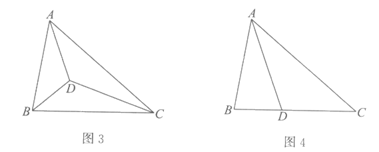
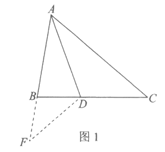
26.课堂上,老师提出了这样一个问题:
如图1,在△ABC中,AD平分∠BAC交BC于点D,且AB+BD=AC.
求证:∠ABC=2∠ACB.
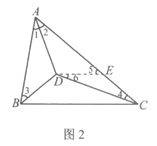
小明的方法是:如图2,在AC上截取AE,使AE=AB,连接DE,构造全等三角形来证明结论.
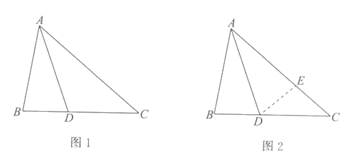
(1)小天提出,如果把小明的方法叫做“截长法“,那么还可以用“补短法“通过延长线段AB构造全等三角形进行证明.辅助线的画法是:延长AB至F,使BF=____________,连接DF.
请补全小天提出的辅助线的画法,并在图1中画出相应的辅助线;
(2)小芸通过探究,将老师所给的问题做了进一步的拓展,给同学们提出了如下的问题:
如图3,点D在△ABC的内部,AD,BD,CD分别平分∠BAC,∠ABC,∠ACB,且AB+BD=AC.求证:∠ABC=2∠ACB.
请你解答小芸提出的这个问题;
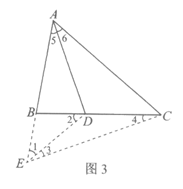
(3)小东将老师所给问题中的一个条件和结论进行交换,得到的命题如下:
如果在△ABC中,∠ABC=2∠ACB,点D在边BC上,AB+BD=AC,那么AD平分∠BAC.
小东判断这个命题也是真命题,老师说小东的判断是正确的.请你利用图4对这个命题进行证明.
数学附加题
试卷满分:20分
一、填空题(本题6分)
1.我们可以将一些只含有一个字母且分子、分母的次数都为一次的分式变形,转化为整数与新的分式的和的形式,其中新的分式的分子中不含字母,如:
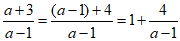 ,
,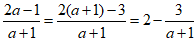 .
.
参考上面的方法,解决下列问题:
(1)将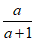 变形为满足以上结果要求的形式:
变形为满足以上结果要求的形式: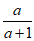 =________________;
=________________;
(2)①将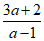 变形为满足以上结果要求的形式:
变形为满足以上结果要求的形式: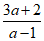 =____________;
=____________;
②若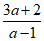 为正整数,且a也为正整数,则a的值为___________.
为正整数,且a也为正整数,则a的值为___________.
二、解答题(本题共14分,第2题6分,第3题8分)
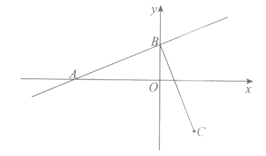
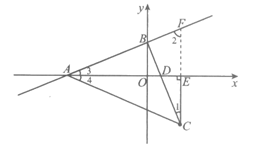
2.如图,在平面直角坐标系xOy中,直线y=kx+3与x轴的负半轴交于点A.与y轴交于点B.点C在第四象限,BC⊥BA,且BC=BA.
(1)点B的坐标为_________,点C的横坐标为_________;
(2)设BC与x轴交于点D,连接AC,过点C作CE⊥x轴于点E.若射线AO平分∠BAC,用等式表示线段AD与CE的数量关系,并证明.
3.在平面直角坐标系xOy中,对于任意两点M(x1,y1),N(x2,y2),定义如下:
点M与点N的“直角距离“为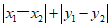 ,记作dMN·
,记作dMN·
例如:点M(1,5)与N(7,2)的“直角距离“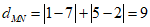 .
.
(1)已知点P1(-1,0),P2(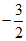 ,
,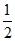 ),P3(
),P3(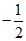 ,
,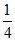 ),P4(
),P4(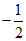 ,
,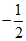 ),则在这四个点中,与原点O的“直角距离“等于1的点是_________;
),则在这四个点中,与原点O的“直角距离“等于1的点是_________;
(2)如图,已知点A(1,0),B(0,1),根据定义可知线段AB上的任意一点与原点O的“直角距离“都等于1.
若点P与原点O的“直角距离“dOP=1,请在图中将所有满足条件的点P组成的图形补全;
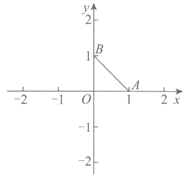
(3)已知直线y=kx+2,点C(t,0)是x轴上的一个动点.
①当t=3时,若直线y=kx+2上存在点D,满足dCD=1,求k的取值范围;
②当k=-2时,直线y=kx+2与x轴,y轴分别交于点E,F.若线段EF上任意一点H都满足1≤dCH≤4,直接写出t的取值范围.
参考答案
一、选择题(本题共30分,每小题3分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | B | C | D | A | B | A | C | B | B | D |
二、填空题(本题共18分,第15,17题每小题3分,其余每小题2分)
11. x≠4. 12.(1,3). 13. -2a. 14.72.
15.12; 答案不唯一,如:小腾家到图书馆的距离为1200米.
16.答案不唯一,如: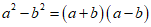 . 17.6;
. 17.6;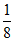 . 18.②,④,⑤.
. 18.②,④,⑤.
(说明:第15,17题第一个空2分,第二个空1分:第18题答对一个得1分,全对得2分)
三、解答题(本题共52分,第19题8分,第20-24题每小题6分,第25,26题每小题7分)
19.解:(1)x3-25x
=x(x2-25) ……………………………………2分
=x(x+5)(x-5). …………………………………4分
(2)m(a-3)+2(3-a)
= m(a-3)- 2(a-3) ……………………………………2分
=(a-3)(m-2).…………………………………………4分
20.解: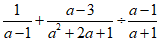
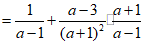 …………………………2分
…………………………2分
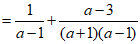 ……………………3分
……………………3分
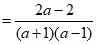 …………………………………………5分
…………………………………………5分
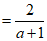 .…………………………6分
.…………………………6分
21.解:(1)补全图形,如图所示: …………………………2分
(2)证明:∵直线MN是线段CB的垂直平分线,
点D在直线MN上,
∴DC=DB.
(线段垂直平分线上的点与这条线段两个端点的距离相等) ……………………3分
∴∠DCB=∠B, ………………………4分
∵∠ACB=90°,
∴∠ACD=90°-∠DCB,
∠A=90°-∠B. ……………………………5分
∴∠ACD=∠A.
∴DC=DA.(等角对等边) …………………………6分
∴△DCB和△DCA都是等腰三角形.
22.解:方程两边同乘x(x-3),…………………………1分
得 x2+x+8=x(x-3). ………………………3分
整理,得4x=-8.
解得x= -2. ……………………………5分
检验:当x=-2时,x(x-3)≠0.
所以,原分式方程的解为x=-2. …………………………6分
23.证明:(1)∵AB∥CD,
∴∠ABC=∠ECD.…………………………1分
在△ABC与△ECD中,
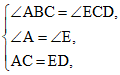
∴△ABC≌△ECD.…………………………………3分
∴BC=CD. …………………………………4分
(2)如图,
∴∠CBD=∠CDB. ………………………………5分
∵∠ABD=∠ABC+∠CBD,
∠EBD=∠BCD+∠CDB,
∴∠ABD=∠EBD.…………………………6分
24.解:(1)∵直线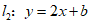 与直线
与直线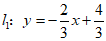 交于点C(-1,m)
交于点C(-1,m)
∴
 …………………………1分
…………………………1分
∴2=2×(-1)+b
∴b=4. …………………………………2分
(2)过点C作CD⊥x轴于点D,如图.
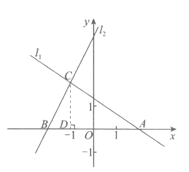
直线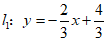 ,当y=0时,x=2;
,当y=0时,x=2;
直线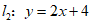 ,当y=0时,x=-2;
,当y=0时,x=-2;
∴A(2,0),B(-2,0).
∴AB=4.
∴
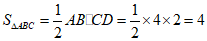 …………………………4分
…………………………4分
(3)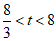 .………………………6分
.………………………6分
25.解:(1)2; ………………………………………………2分
(2)①1或-1; ……………………………………………4分
②3; …………………………………………5分
(3)设直线l的表达式为y=kx+b.
∵直线l经过点C(0,3)和D(4,0),
∴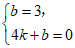
解得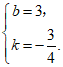
∴直线l的表达式为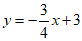 . ……………………6分
. ……………………6分
∵点P(m,n)是线段CD上的一个动点,
∴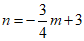
如图,当OE=PE时,点O,E,P的“最佳间距“取到最大值.
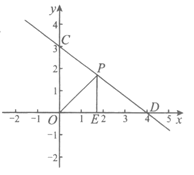
∴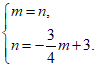
解得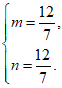
∴此时点P的坐标为(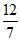
,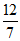
). ………………7分
26.解:(1) BD,…………………………………1分
如图1所示; ………………2分
(2)证明:在AC上截取AE,使AE=AB,连接DE,
如图2.
则AC=AE+EC=AB+EC.
∵AC=AB+BD,
∴EC=BD.
∵AD, BD, CD分别平分∠BAC, ∠ABC, ∠ACB,
∴∠1=∠2,∠ABC=2∠3, ∠ACB=2∠4.
在△ABD与△AED中,
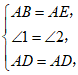
∴△ABD≌△AED.
∴∠3=∠5,BD=ED.
∴EC=ED.
∴∠4=∠6.
∴∠5=∠4+∠6=2∠4=∠ACB.
∴∠3=∠ACB.
∴∠ABC=2∠3=2∠ACB.………………………5分
(3)证明:延长AB至E,使BE=BD,连接ED,EC,如图3.
∵BE=BD,
∴∠1=∠2.
∴∠ABC=∠1+∠2=2∠1.
∵∠ABC=2∠ACB,
∴∠1=∠ACB.
∵AE=AB+BE=AB+BD=AC,
∴∠AEC=∠ACE.
∵∠3=∠AEC-∠1,∠4=∠ACE-∠ACB,
∴∠3=∠4.
∴DE=DC.
在△AED与△ACD中,
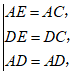
∴△AED≌△ACD.
∴∠5=∠6.
∴AD平分∠BAC. ………………………………7分
附加题参考答案
一、填空题(本题6分)
1.解:(1)
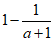 ;…………………………………………………2分
;…………………………………………………2分
(2)①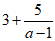 ;…………………………………………………4分
;…………………………………………………4分
②2或6. …………………………………………………6分
二、解答题(本题共14分,第2题6分,第3题8分)
2.解:(1)(0,3), ……………………………………………………2分
3; ……………………………………………………3分
(2) AD=2CE. ……………………………………………………4分
证明:延长CE交直线AB于点F,如图.
∵BC⊥BA,
∴∠ABD=∠CBF=90°.
∴∠1+∠2=90°.
∵CE⊥x轴于点E,
∴∠AEF=∠AEC=90°.
∴∠3+∠2=90°.
∴∠3=∠1.
在△ABD与△CBF中,
∴△ABD≌△CBF.
∴AD=CF.
∵射线AD平分∠BAC,
∴∠3=∠4.
∴∠2=∠ACE.
∴AF=AC.
∴CF=2CE.
∴AD=2CE. ………………………………………………6分
3.解:(1) P1,P4; ……………………………………2分
(2)如图1所示; ………………………………4分
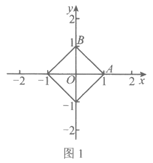
(3)①如图2,与点C的“直角距离“等于1的点组成的图形是四边形MNST.
当直线y=kx+2经过点M(3,1)时,
l=3k+2,解得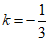 ;
;
当直线y=kx+2经过点N(2,0)时,
0=2k+2,解得k=-1,
此时点S(3,-1)也在这条直线上,
∵直线y=kx+2上存在点D,满足dCD=1,
∴k的取值范围是
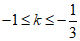 . ……………6分
. ……………6分
②-2≤t≤0或t=2. …………………8分
