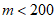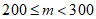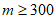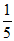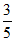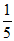本试卷共150分。考试时长120分钟。
第一部分(选择题
共40分)
一、选择题:共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 已知集合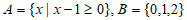 ,则
,则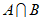 =
=
A. {0} B. {1} C. {2} D. {1,2}
2. 已知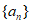 是公差为d的等差数列,
是公差为d的等差数列,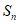 为其前n项和,若
为其前n项和,若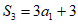 ,则
,则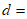
A. -2 B. -1 C. 1 D. 2
3. 下列函数中,既是奇函数,又在区间(0,1)上单调递增的是
A. 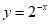 B.
B. 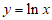 C.
C. 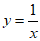 D.
D.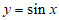
4. 将正方体去掉一个四棱锥,得到的几何体如图所示,该几何体的侧(左)视图为
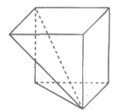
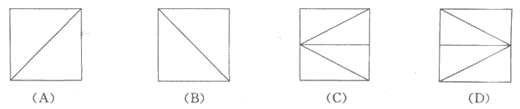
5. 与圆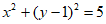 相切于点(2,2)的直线的斜率为
相切于点(2,2)的直线的斜率为
A. -2 B. 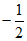 C.
C. 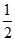 D. 2
D. 2
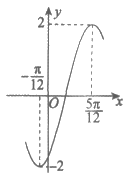
6. 函数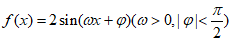 的部分图象如图所示,则
的部分图象如图所示,则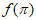 =
=
A. 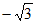 B.
B. 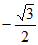 C.
C. 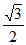 D.
D.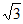
7. 设a,b是两个不共线向量,则”a与b的夹角为锐角”是”a⊥(a-b)”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
8. 十二生肖,又叫属相,依次为鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪,现有十二生肖的吉祥物各一个,甲、乙、丙三名同学从中各选一个,甲没有选择马,乙、丙二人恰有一人选择羊,则不同的选法有
A. 242种 B. 220种 C. 200种 D. 110种
9. 已知抛物线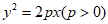 的焦点F到准线的距离为2,过焦点F的直线与抛物线交于A,B两点,且
的焦点F到准线的距离为2,过焦点F的直线与抛物线交于A,B两点,且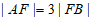 ,则点A到y轴的距离为
,则点A到y轴的距离为
A. 5 B. 4 C. 3 D. 2
10. 某公园门票单价30元,相关优惠政策如下:
①10人(含)以上团体购票9折优惠;
②50人(含)以上团体购票8折优惠;
③100人(含)以上团体购票7折优惠;
④购票总额每满500元减100元(单张票价不优惠)。
现购买47张门票,合理地设计购票方案,则门票费用最少为
A. 1090元 B. 1171元 C. 1200元 D. 1210元
第二部分(非选择题
共110分)
二、填空题:共5小题,每小题5分,共25分。
11. 复数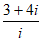 =_____________。
=_____________。
12. 函数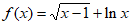 的定义域是_____________。
的定义域是_____________。
13. 已知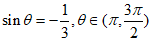 ,则
,则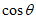 =___________,
=___________,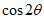 =___________。
=___________。
14. 已知双曲线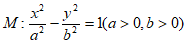 ,△ABC为等边三角形,若点A在y轴上,点B,C在双曲线M上,且双曲线M的实轴为△ABC的中位线,则双曲线M的离心率为_________。
,△ABC为等边三角形,若点A在y轴上,点B,C在双曲线M上,且双曲线M的实轴为△ABC的中位线,则双曲线M的离心率为_________。
15. 已知函数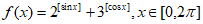 ,其中
,其中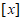 表示不超过x的最大整数。
表示不超过x的最大整数。
例如: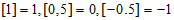 。
。
①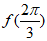 =____________;
=____________;
②若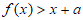 对任意
对任意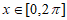 都成立,则实数a的取值范围是__________。
都成立,则实数a的取值范围是__________。
三、解答题:共6小题,共85分,解答应写出文字说明、演算步骤或证明过程。
16.(本小题13分)
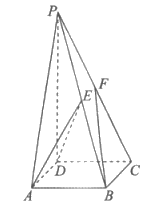
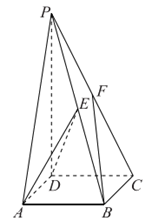
如图,在四棱锥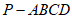 中,PD⊥平面ABCD,PD=4,底面ABCD是边长为2的正方形,E,F分别为PB,PC的中点。
中,PD⊥平面ABCD,PD=4,底面ABCD是边长为2的正方形,E,F分别为PB,PC的中点。
(Ⅰ)求证:平面ADE⊥平面PCD;
(Ⅱ)求直线BF与平面ADE所成角的正弦值。
17.(本小题13分)
已知函数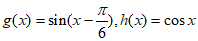 ,再从条件①、条件②这两个条件中选择一个作为已知,求:
,再从条件①、条件②这两个条件中选择一个作为已知,求:
(Ⅰ)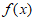 的最小正周期;
的最小正周期;
(Ⅱ)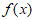 在区间
在区间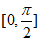 上的最大值。
上的最大值。
条件①: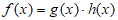 ;
;
条件②: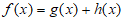 。
。
注:如果选择条件①和条件②分别解答,按第一个解答计分。
18.(本小题14分)
为了解果园某种水果产量情况,随机抽取100个水果测量质量,样本数据分组为[100,150),[150,200),[200,250),[250,300),[300,350),[350,400](单位:克),其频率分布直方图如图所示:
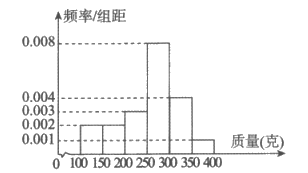
(Ⅰ)用分层抽样的方法从样本里质量在[250,300),[300,350)的水果中抽取6个,求质量在[250,300)的水果数量;
(Ⅱ)从(Ⅰ)中得到的6个水果中随机抽取3个,记X为质量在[300,350)的水果数量,求X的分布列和数学期望;
(Ⅲ)果园现有该种水果约20 000个,其等级规格及销售价格如下表所示,
质量m(单位:克) |
|
|
|
等级规格 | 二等 | 一等 | 特等 |
价格(元/个) | 4 | 7 | 10 |
试估计果园该种水果的销售收入。
19.(本小题15分)
已知椭圆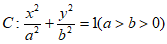 过点
过点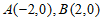 ,且离心率为
,且离心率为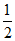 。
。
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线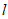 与椭圆C有且仅有一个公共点E,且与x轴交于点G(E,G不重合),ET⊥x轴,垂足为T。求证:
与椭圆C有且仅有一个公共点E,且与x轴交于点G(E,G不重合),ET⊥x轴,垂足为T。求证: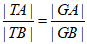 。
。
20.(本小题15分)
已知函数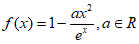 。
。
(Ⅰ)若曲线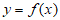 在点
在点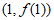 处的切线平行于直线
处的切线平行于直线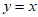 ,求该切线方程;
,求该切线方程;
(Ⅱ)若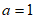 ,求证:当
,求证:当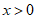 时,
时,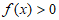 ;
;
(Ⅲ)若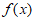 恰有两个零点,求a的值。
恰有两个零点,求a的值。
21.(本小题15分)
给定正整数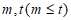 ,若数列
,若数列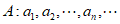 满足:
满足: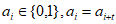 ,
,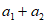
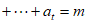 ,则称数列A具有性质
,则称数列A具有性质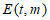 。
。
对于两个数列B: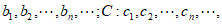
定义数列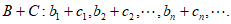
(Ⅰ)设数列A具有性质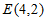 ,数列B的通项公式为
,数列B的通项公式为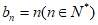 ,求数列
,求数列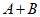 的前四项和;
的前四项和;
(Ⅱ)设数列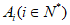 具有性质
具有性质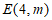 ,数列B满足
,数列B满足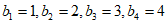 且
且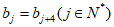 ,若存在一组数列
,若存在一组数列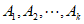 ,使得
,使得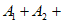 …
…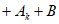 为常数列,求出m所有可能的值;
为常数列,求出m所有可能的值;
(Ⅲ)设数列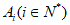 具有性质
具有性质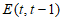 (常数
(常数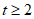 ),数列B满足
),数列B满足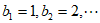
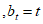 且
且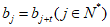 ,若存在一组数列
,若存在一组数列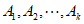 ,使得
,使得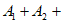 …
…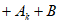 为常数列,求k的最小值。(只需写出结论)
为常数列,求k的最小值。(只需写出结论)
【试题答案】
一、选择题(共10小题,每小题4分,共40分)
1. D 2. C 3. D 4. B 5. A
6. A 7. B 8. C 9. C 10. B
二、填空题(共5小题,每小题5分,共25分)
11. 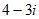 12.
12. 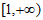 13.
13. 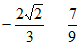 14.
14.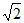
15. 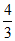
三、解答题(共6小题,共85分)
16.(共13分)
解:(Ⅰ)因为PD⊥平面ABCD,
所以PD⊥AD,
因为底面ABCD是正方形,
所以AD⊥CD,
因为 ,
,
所以AD⊥平面PCD,
又因为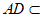 平面ADE,
平面ADE,
所以平面ADE⊥平面PCD。 4分
(Ⅱ)因为PD⊥底面ABCD,
所以PD⊥AD,PD⊥CD,
因为底面ABCD是正方形,所以AD⊥CD。
如图建立空间直角坐标系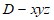 。
。
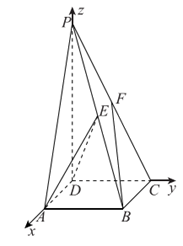
因为PD=4,底面ABCD为边长为2的正方形,
所以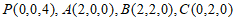 ,
,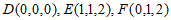 ,
,
则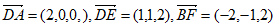 。
。
设平面ADE的法向量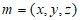 ,
,
由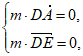 可得
可得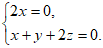
令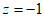 ,则
,则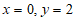 ,
,
所以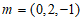 。
。
设直线BF与平面ADE所成角为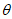 ,
,
则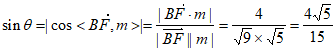 ,
,
所以直线BF与平面ADE所成角的正弦值为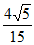 。 13分
。 13分
17.(共13分)
解:选条件①: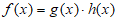 ;
;
(Ⅰ)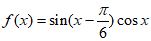
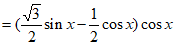
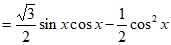
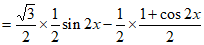
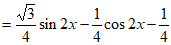
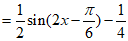 。
。
所以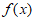 的最小正周期是
的最小正周期是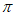 。 7分
。 7分
(Ⅱ)因为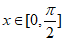 ,
,
所以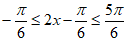 ,
,
所以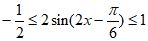 ,
,
所以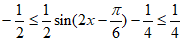 ,
,
当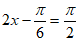 ,即
,即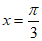 时,
时,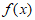 有最大值
有最大值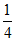 。 13分
。 13分
选条件②: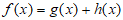 。
。
(Ⅰ)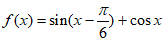
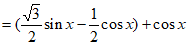
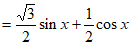
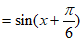 。
。
所以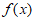 的最小正周期是
的最小正周期是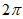 。 7分
。 7分
(Ⅱ)因为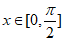 ,
,
所以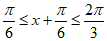 ,
,
所以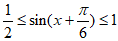 ,
,
当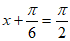 ,即
,即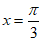 时,
时,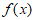 有最大值1。 13分
有最大值1。 13分
18.(共14分)
解:(Ⅰ)质量在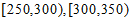 的该种水果的频率分别为
的该种水果的频率分别为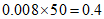 ,
,
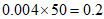 ,其比为2:1,
,其比为2:1,
所以按分层抽样从质量在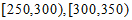 的这种水果中随机抽取6个,
的这种水果中随机抽取6个,
质量在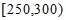 的该种水果有4个。 4分
的该种水果有4个。 4分
(Ⅱ)由(Ⅰ)可知,6个水果中有2个质量在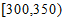 ,
,
所以X的所有可能取值为0,1,2,
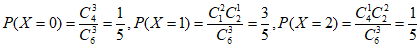 。
。
所以X的分布列为
X | 0 | 1 | 2 |
P |
|
|
|
故X的数学期望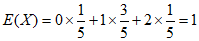 。 10分
。 10分
(Ⅲ)由频率分布直方图可知,质量在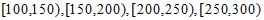 ,
,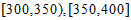 的该种水果的频率分别为0.1,0.1,
的该种水果的频率分别为0.1,0.1,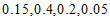 ,
,
所以估计20000个水果中,二等品有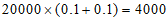 个;
个;
一等品有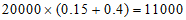 个;
个;
特等品有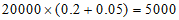 个。
个。
果园该种水果的销售收入为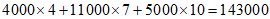 (元)。 14分
(元)。 14分
19.(共15分)
解:(Ⅰ)依题意,得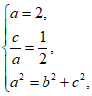
解得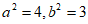 ,
,
所以椭圆C的方程为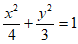 。 4分
。 4分
(Ⅱ)由题设知直线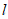 的斜率存在,设直线
的斜率存在,设直线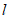 的方程为:
的方程为: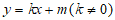 ,
,
由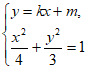 消去y,整理得
消去y,整理得 。
。
依题意,有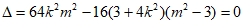 ,解得
,解得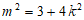 。
。
设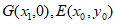 ,则
,则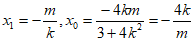 ,
,
因为ET⊥x轴,所以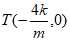 ,
,
所以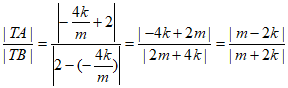 。
。
又因为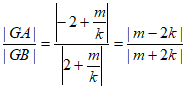 ,
,
所以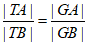 。 15分
。 15分
20.(共15分)
解:(Ⅰ)因为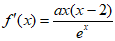 ,所以
,所以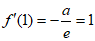 ,故
,故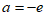 ,
,
所以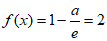 ,
,
所以切线方程为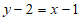 ,即
,即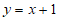 。 4分
。 4分
(Ⅱ)当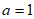 时,
时,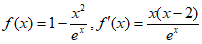 ,
,
当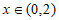 时,
时,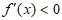 ;当
;当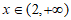 时,
时,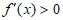 ,
,
所以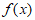 在区间(0,2)上单调递减,在区间
在区间(0,2)上单调递减,在区间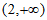 上单调递增,
上单调递增,
所以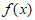 的最小值为
的最小值为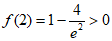 ,
,
故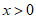 时,
时,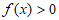 。 10分
。 10分
(Ⅲ)对于函数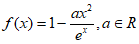 。
。
(i)当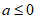 时,
时,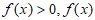 没有零点;
没有零点;
(ii)当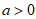 时,
时,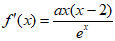 。
。
当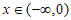 时,
时,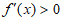 ,所以
,所以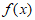 在区间
在区间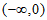 上单调递增;
上单调递增;
当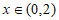 时,
时,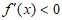 ,所以
,所以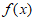 在区间(0,2)上单调递减;
在区间(0,2)上单调递减;
当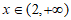 时,
时,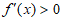 ,所以
,所以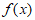 在区间
在区间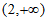 上单调递增,
上单调递增,
所以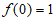 是
是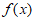 的极大值,
的极大值,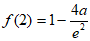 是
是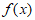 的极小值。
的极小值。
因为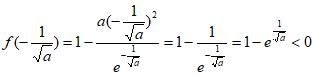 ,
,
所以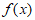 在
在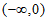 上有且只有一个零点。
上有且只有一个零点。
由于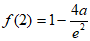 ,
,
①若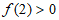 ,即
,即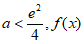 在区间
在区间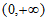 上没有零点;
上没有零点;
②若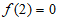 ,即
,即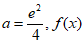 在区间
在区间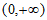 上只有一个零点;
上只有一个零点;
③若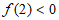 ,即
,即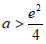 ,由于
,由于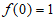 ,所以
,所以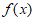 在区间
在区间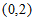 上有一个零点。
上有一个零点。
由(Ⅱ)知,当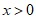 时,
时,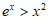 ,
,
所以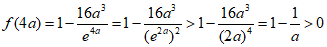 ,
,
故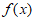 在区间
在区间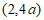 上有一个零点,
上有一个零点,
因此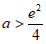 时,
时,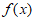 在区间
在区间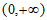 上有两个零点。
上有两个零点。
综上,当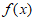 有两个零点时,
有两个零点时,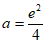 。 15分
。 15分
21.(共15分)
解:(Ⅰ)数列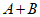 的前四项和为A的前四项和与B的前四项和之和,为2+10=12。
的前四项和为A的前四项和与B的前四项和之和,为2+10=12。
4分
(Ⅱ)由题知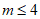 ,数列
,数列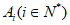 满足:
满足: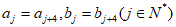 ,所以只考虑数列
,所以只考虑数列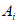 和
和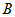 的前四项,
的前四项,
取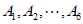 为
为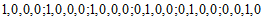 ,可使
,可使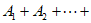
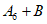 的前四项为4,4,4,4,所以m=1成立;
的前四项为4,4,4,4,所以m=1成立;
取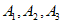 为1,1,0,0;1,1,0,0;1,0,1,0,可使
为1,1,0,0;1,1,0,0;1,0,1,0,可使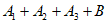 的前四项为4,4,4,4,所以
的前四项为4,4,4,4,所以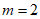 成立;
成立;
取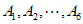 为
为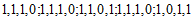 ;
;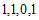 ,可使
,可使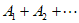
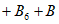 的前四项为
的前四项为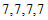 ,所以
,所以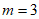 成立;
成立;
当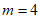 时,
时,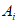 前四项是
前四项是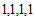 ,所以对任意的
,所以对任意的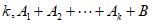 不会是常数列;
不会是常数列;
综上,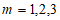 。 12分
。 12分
(Ⅲ)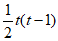 。 15分
。 15分