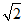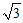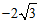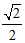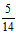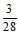本试卷考试时长120分钟,满分150分。
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1.在复平面内,复数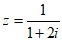 对应的点位于( )
对应的点位于( )
(A)第一象限 (B)第一象限 (C)第一象限 (D)第一象限
2.椭圆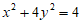 的离心率为( )
的离心率为( )
(A)
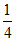 (B)
(B)
 (C)
(C)
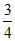
(D)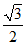
3.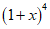 的展开式中x2的系数是( )
的展开式中x2的系数是( )
(A)8 (B)7 (C)6 (D)4
4.某批数量很大的产品的次品率为p,从中任意取出4件,则其中恰好含有3件次品的概率是( )
(A) p3 (B)p3(1-p) (C)
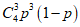 (D)
(D)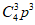
5.已知抛物线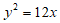 的焦点为F,点P在抛物线上且横坐标为3,则|PF|等于( )
的焦点为F,点P在抛物线上且横坐标为3,则|PF|等于( )
(A)4 (B)6 (C)8 (D) 10
6.已知双曲线
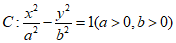 的一条渐近线方程为
的一条渐近线方程为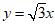 ,一个焦点坐标为(2,0),则双曲线C的方程为( )
,一个焦点坐标为(2,0),则双曲线C的方程为( )
(A)
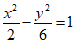 (B)
(B)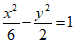 (C)
(C)
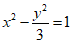 (D)
(D)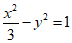
7.已知m,n表示两条不同直线,α表示平面,下列说法正确的是( )
(A)若m∥α,n∥α,则m∥n (B)若m⊥α,n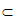 α,则m⊥n
α,则m⊥n
(C)若m⊥α,m⊥n,则n∥α (D)若m∥α ,m⊥n,则n⊥α
8.已知F1,F2是椭圆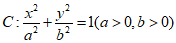 的左,右焦点,A是C的左顶点,点P在过A且斜率为
的左,右焦点,A是C的左顶点,点P在过A且斜率为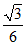 的直线上,△PF1F2为等腰三角形,∠F1F2P=120°,则C的离心率为( )
的直线上,△PF1F2为等腰三角形,∠F1F2P=120°,则C的离心率为( )
(A)
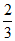 (B)
(B)
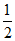 (C)
(C)
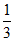 (D)
(D)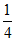
9.万历十二年,中国明代音乐理论家和数学家朱载堉在其著作《律学新说》中,首次用珠算开方的办法计算出了十二个半音音阶的半音比例,这十二个半音音阶称为十二平均律.十二平均律包括六个阳律(黄钟、太族、姑洗、蕤宾、夷则、无射)和六个阴律(大吕、夹钟、仲吕、林钟、南吕、应钟).现从这十二平均律中取出2个阳律和2个阴律,排成一个序列,组成一种旋律,要求序列中的两个阳律相邻,两个阴律不相邻,则可组成不同的旋律( )
(A) 450种 (B) 900种 (C) 1350种 (D) 1800种
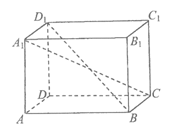
10.在正方体ABCD-A1B1C1D1中,在正方形DD1C1C中有一动点P,满足PD1⊥PD,则直线PB与平面DD1C1C所成角中最大角的正切值为( )
(A)1 (B)
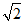 (C)
(C)
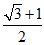 (D)
(D)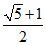
二、填空题
共6小题,每小题5分,共30分。
11.若复数z=i·(1-i),则|z|=____________.
12.若直线2x-y-5=0与直线x+ay+3=0相互垂直,则实数a=____________.
13.盒子里有20个形状、大小、质地相同的小球,其中有8个白色的,6个红色的,6个黑色的,从盒子里任意取出一个球,已知这个球不是黑球,则取出的球是红球的概率是____________.
14.如图,在长方体ABCD-A1B1C1D1中,设AD=AA1=1,AB=2,则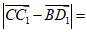 ____________,
____________,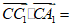 ____________.
____________.
15.已知椭圆C1,抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为坐标原点.右表给出坐标的五个点中,有两个点在C1上,另有两个点在C2上.则椭圆C1的方程为____________ ,C1的左焦点到C2的准线之间的距离为____________.
x | 1 | 3 | -2 | 4 |
|
y |
|
| 0 | -4 |
|
16.已知曲线C的方程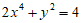 ,有以下说法:
,有以下说法:
①曲线C过原点
②曲线C与x轴有两个交点
③曲线C关于x轴,y轴对称
④P(x,y)为曲线C上任意一点,则|y|≤1
请写出所有正确的序号________________.
三、解答题
共6小题,共80分。解答应写出文字说明、演算步骤或证明过程。
17.某工厂生产一种汽车的元件,该元件是经过A、B、C三道工序加工而成的,A、B、C三道工序加工的元件合格率分别为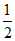 、
、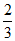 、
、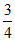 ,已知每道工序的加工都相互独立,三道工序加工都合格的元件为一等品;恰有两道工序加工合格的元件为二等品;其它的为废品,不进入市场.
,已知每道工序的加工都相互独立,三道工序加工都合格的元件为一等品;恰有两道工序加工合格的元件为二等品;其它的为废品,不进入市场.
(I)生产一个元件,求该元件为一等品的概率;
(II)生产一个元件,求该元件为二等品的概率;
(III)若从该工厂生产的这种元件中任意取出3个元件进行检测,求至少有2个元件是一等品的概率。
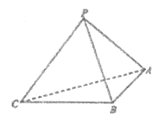
18.已知三棱锥P-ABC中,PA=PB=PC=AB=BC= 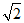 ,AC=2.
,AC=2.
(I)求证:平面PAC⊥平面ABC;
(II)求二面角A-PC-B的余弦值;
(III)若点M在线段PC上,满足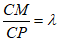 ,
,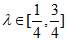 ,点N在线段PB上,且BM⊥AN,求
,点N在线段PB上,且BM⊥AN,求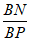 的取值范围.
的取值范围.
19.2019年底,北京2022年冬奥组委会启动志愿者全球招募,仅一个月内报名人数便突破60万,其中青年学生约有50万人.现从这50万青年学生志愿者中,按男女分层抽样随机选取20人进行英语水平测试,所得成绩(单位:分)统计结果用茎叶图记录如下:
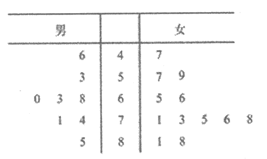
(I)试估计在这50万青年学生志愿者中,英语测试成绩在80分以上的女生人数;
(II)从选出的8名男生中随机抽取2人,记其中测试成绩在70分以上的人数为X,求X的分布列和数学期望;
(III)为便于联络,现将所有的青年学生志愿者随机分成若干组(每组人数不少于5000),并在每组中随机选取m个人作为联络员,要求每组的联络员中至少有1人的英语测试成绩在70分以上的概率大于90%.根据图表中数据,以频率作为概率,给出m的最小值.(结论不要求证明)
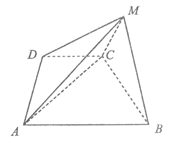
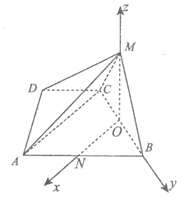
20.如图,在四棱锥M-ABCD中,AB∥CD,∠ADC=∠BMC=90°,MB=MC,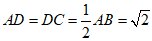 ,平面BCM⊥平面ABCD.
,平面BCM⊥平面ABCD.
(I)求证:CD∥平面ABM:
(II)求证:AC⊥平面BCM;
(III)在棱AM上是否存在一点E,使得二面角E-BC-M的大小为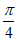 ?若存在,求出
?若存在,求出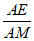 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
21.已知椭圆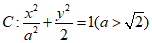 的离心率为
的离心率为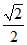 ,左、右顶点分别为A,B,点M是椭圆C上异于A,B的一点,直线AM与y轴交于点P.
,左、右顶点分别为A,B,点M是椭圆C上异于A,B的一点,直线AM与y轴交于点P.
(I)求椭圆C的方程;
(II)若点P在椭圆C的内部,求直线AM的斜率的取值范围;
(III)设椭圆C的右焦点为F,点Q在y轴上,且∠PFQ= 90°,求证:AQ∥BM.
22.已知椭圆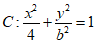 的左顶点A与上顶点B的距离为
的左顶点A与上顶点B的距离为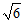 .
.
( I)求椭圆C的方程和焦点的坐标。
( II)点P在椭圆C上,且点P不在x轴上,线段AP的垂直平分线与y轴相交于点Q,若△PAQ为等边三角形,求点P的横坐标.
参考答案
一、选择题
共10小题,每小题4分,共40分。
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
A | D | C | C | B | C | B | D | B | D |
二、填空题
共6小题,每小题5分,共30分。
11.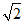 12.2; 13.
12.2; 13.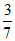
14.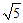 ,1; 15.
,1; 15.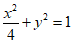 ,
,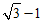 16.②③;
16.②③;
三、解答题
共6小题,共80分。解答应写出文字说明、演算步骤或证明过程。
17.解:(I)不妨设元件经A,B,C三道工序加工合格的事件分别为A,B,C.
所以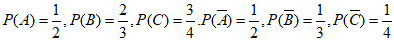 .
.
则该元件为一等品的概率为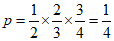 .
.
(II)设事件D为“生产一个元件,该元件为二等品“.
由已知A,B,C是相互独立事件.
根据事件的独立性、互斥事件的概率运算公式,
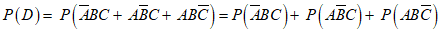
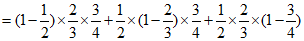
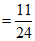 .
.
所以生产一个元件,该元件为二等品的概率为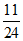 .
.
(III)生产一个元件,该元件为一等品的概率为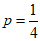 .
.
设事件E为“任意取出3个元件进行检测,至少有2个元件是一等品“,则
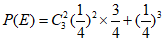
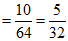 .
.
所以至少有2个元件是一等品的概率为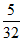 .
.
18.解:
(I)
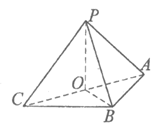
设AC的中点为O,连接BO,PO.由题意
PA=PB=PC=
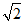 ,PO =1,AO=BO=CO=1
,PO =1,AO=BO=CO=1
因为在△PAC中,PA=PC,O为AC的中点
所以PO⊥AC,
因为在△POB中,PO=1,OB=1,PB=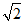
所以PO⊥OB
因为AC
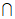 OB=O,AC,OB
OB=O,AC,OB 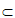 平面ABC
平面ABC
所以PO⊥平面ABC
因为PO
 平面PAC
平面PAC
所以平面PAC⊥平面ABC
(II)由PO⊥平面ABC,OB⊥AC,如图建立空间直角坐标系,则
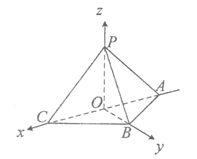
O(0,0,0),C(1,0,0),B(0,1,0),A(-1,0,0),P(0,0,1)
由OB⊥平面APC,故平面APC的法向量为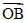 =(0,1,0)
=(0,1,0)
由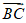 =(1,-1,0),
=(1,-1,0),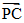 =(1,0,-1)
=(1,0,-1)
设平面PBC的法向量为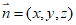 ,则
,则
由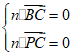
得: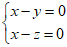
令x=1,得y=1,z=1,即
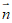 =(1,1,1)
=(1,1,1)
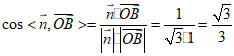 ,由于二面角A-PC-B是锐二面角,所以二面角A-PC-B的余弦值是
,由于二面角A-PC-B是锐二面角,所以二面角A-PC-B的余弦值是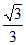 ;
;
(III)设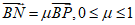 ,则
,则
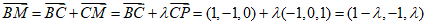
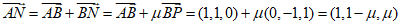
令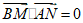
得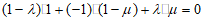
即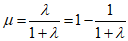 ,μ是关于λ的单调递增函数,
,μ是关于λ的单调递增函数,
当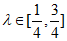 时,
时,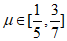 ,
,
所以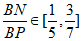 .
.
19.解:(I)由图表可知,测试成绩在80分以上的女生有2人,占比为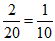 ,
,
故在这50万青年学生志愿者中,英语测试成绩在80分以上的女生约为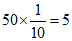 万人.
万人.
(II)由图表知,选取的8名男生中,成绩在70分以上的有3人,70分及其以下的有5人,
由题意,随机变量X的所有可能取值为:0,1,2.
且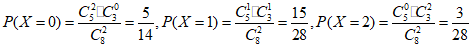 .
.
所以随机变量X的分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
所以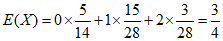
(III)m的最小值为4.
20.证明:(I)因为AB∥CD,
AB
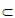
平面ABM,
CD
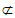 平面ABM,
平面ABM,
所以CD∥平面ABM.
(II)取AB的中点N,连接CN.
在直角梯形ABCD中,
易知AN=BN=CD=
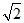 ,且CN⊥AB,
,且CN⊥AB,
在Rt△CNB中,由勾股定理得BC=2.
在△ACB中,由勾股定理逆定理可知AC⊥BC.
又因为平面BCM⊥平面ABCD,
且平面BCM
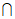 平面ABCD=BC,
平面ABCD=BC,
所以AC⊥平面BCM. …………7分
(III)取BC的中点O,连接OM,ON.
所以ON∥AC,
因为AC⊥平面BCM,
所以ON⊥平面BCM.
因为BM=MC,
所以OM⊥BC.
如图建立空间直角坐标系O-xyz,
则M(0,0,1),B(0,1,0),C(0,-1,0),A(2,-1,0),
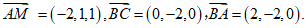
易知平面BCM的一个法向量为m=(1,0,0).
假设在棱AM上存在一点E,使得二面角E-BC-M的大小为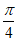
不妨设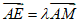 (0≤λ≤1),
(0≤λ≤1),
所以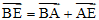 =(2-2λ,λ-2,λ),
=(2-2λ,λ-2,λ),
设n=(x,y,z)为平面BCE的一个法向量,
则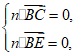 即
即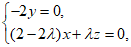
令x=λ,z=2λ-2,所以n=(λ,0,2λ-2).
从而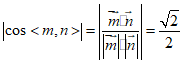 .
.
解得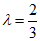
或λ=2.
因为0≤λ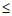 1,所以λ=
1,所以λ=
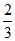 .
.
由题知二面角E-BC-M为锐二面角,
所以在棱AM上存在一点E,使得二面角E-BC-M的大小为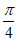 ,
,
此时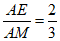 .
.
21.解:(I)由题意,得c2=a2-2,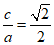 ,
,
解得a=2,c=
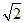 ,所以椭圆C的方程为
,所以椭圆C的方程为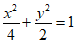 .
.
( II)设P(0,m),由点P在椭圆C的内部,得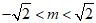 ,
,
又因为A(-2,0),
所以直线AM的斜率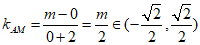 ,
,
又因为M是椭圆C上异于A,B的一点,
所以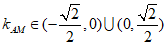 .
.
(III)由题意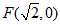 ,设Q(0,y1),M(x0,y0),其中x0≠±2,
,设Q(0,y1),M(x0,y0),其中x0≠±2,
则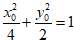
直线AM的方程为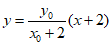
令x=0,得点P的坐标为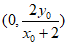
由∠PFQ=90°,得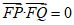 ,
,
所以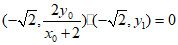 ,
,
即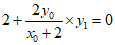 ,解得
,解得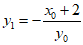 ,所以
,所以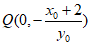 .
.
因为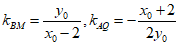 ,
,
所以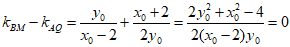
故kBM=kAQ,即AQ//BM.
22.解:(I)依题意,有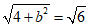
所以b2 =2
所以椭圆方程为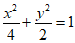
所以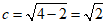
焦点坐标分别为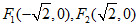 ,
,
(II)设P(x0,y0),则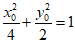 ,且A(-2,0),x0≠±2,y0≠0.
,且A(-2,0),x0≠±2,y0≠0.
设线段PA中点为M,所以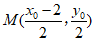
因为PA⊥MQ,所以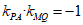
因为直线PA的斜率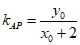
所以直线MQ的斜率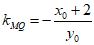
又直线MQ的方程为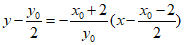
令x=0,得到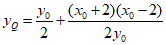
因为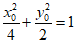
所以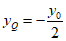
因为△PAQ为正三角形,
所以|AP|=|AQ|,即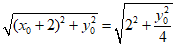
化简,得到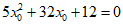 ,解得
,解得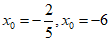 (舍)
(舍)
即点P的横坐标为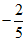 .
.