一、选择题:本大题共12小题,共24分。
1. 月球与地球的距离大约是384400千米,用科学记数法表示为(
)千米。
A. 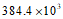 B.
B.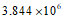
C. 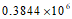 D.
D.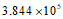
2. 下列关于单项式2x2y的说法正确的是(
)
A. 系数是1,次数是2 B. 系数是2,次数是2
C. 系数是1,次数是3 D. 系数是2,次数是3
3. 下列式子的变形中,正确的是(
)
A. 由6+x=10得x=10+6 B. 由3x+5=4x得3x–4x=–5
C. 由8x=4–3x得8x–3x =4 D. 由2(x–1)= 3得2x–1=3
4. 方程x+y=6的正整数解有(
)
A. 5个 B. 6个 C. 7个 D. 无数个
5. 下图是由几个相同的正方体搭成的一个几何体,从正面看得到的平面图形是(
)
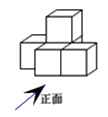













A. B. C. D.
6. 将一副三角板按如下图所示位置摆放,已知∠α=30°14′,则∠β的度数为(
)
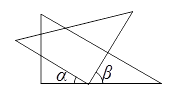
A. 75°14′ B. 59°86′ C. 59°46′ D. 14°46′
7. 根据” x的3倍比x的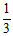 多2″可列方程为(
多2″可列方程为(
)
A. 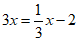 B.
B.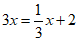
C. 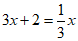 D.
D.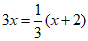
8. 若方程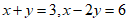 和
和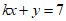 有公共解,则
有公共解,则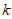 的值是(
的值是(
)
A. 1 B. -1 C. 2 D. -2
9. 有理数a、b、c、d在数轴上的对应点的位置如图所示,则正确的结论是(
)

A. 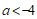 B.
B. 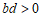 C.
C. 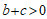 D.
D.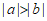
10. 如下图,直线AB与CD相交于点O,OE平分∠AOC,且∠BOE=140°,则∠BOC为(
)
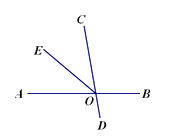
A. 140° B. 100° C. 80° D. 40°
11. 在某场CBA比赛中,某位运动员的技术统计如下表所示:
技术 | 上场时间(分钟) | 出手投篮(次) | 投中(次) | 罚球得分(分) | 篮板(个) | 防攻(次) | 个人总得分(分) |
数据 | 38 | 27 | 11 | 6 | 3 | 4 | 33 |
注:①表中出手投篮次数和投中次数均不包括罚球;
②总得分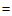 两分球得分
两分球得分 三分球得分
三分球得分 罚球得分。
罚球得分。
根据以上信息,本场比赛中该运动员投中两分球和三分球各(
)个。
A. 5,6 B. 6,5 C. 4,7 D. 7,4
12. 如图,点M在线段AN的延长线上,且线段MN=20,第一次操作:分别取线段AM和AN的中点M1,N1;第二次操作:分别取线段AM1和AN1的中点M2,N2;第三次操作:分别取线段AM2和AN2的中点M3,N3;连续这样操作10次,则M10N10=(
)
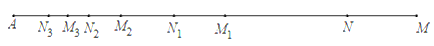
A. 2 B. 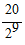 C.
C. 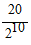 D.
D.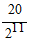
二、填空题:本大题共8小题,共24分。
13. 写出一个以
为解的二元一次方程组:
。
14. 如果x=1是关于x的方程5x+2m–7=0的根,则m的值是
。
15. 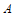 、
、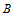 、
、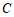 三点相对于海平面分别是
三点相对于海平面分别是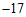 米,
米,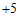 米,
米,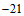 米,那么最高的地方比最低的地方高
米,那么最高的地方比最低的地方高
米。
16. 如图是一数值转换机的示意图,若输入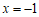 ,则输出的结果是
,则输出的结果是
。

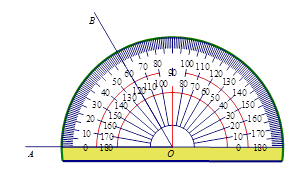
17. ∠AOB的大小可由量角器测得(如图所示),则∠AOB的补角的大小为
 。
。
18. 已知∠AOB=60°,自∠AOB的顶点O引射线OC,若∠AOC:∠AOB=1:4,那么∠BOC的度数是__________。
19. 已知二元一次方程组为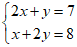 ,
,
则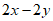 的值为__________。
的值为__________。
20. 用“☆“定义一种新运算:对于任意有理数a和b,规定a☆b=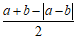 。
。
例如:(-1)☆2 =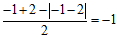 。
。
(1)计算:(-6)☆(-8)=
。
(2)从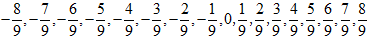 中任选两个有理数作为a和b,并计算a☆b,那么所有运算结果中的最大值是__________。
中任选两个有理数作为a和b,并计算a☆b,那么所有运算结果中的最大值是__________。
三、解答题:本大题共8小题,共52分。
21. (4分)计算: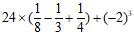 。
。
22. (12分)解下列方程或方程组:
(1)4x-2 =2x+3。
(2)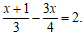
(3)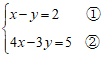 。
。
23. (6分)先化简,再求值: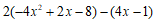 ,其中
,其中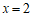 。
。
24. (6分)如图,已知直线l和直线外三点A、B、C,按下列要求画图:
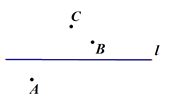
(1)画射线AB;
(2)画线段BC;
(3)用圆规在BC延长线上截取CD=BC;
(4)在直线l上确定点E,使得AE+CE最小,
并说明你的作图依据
。
25. (6分)如图,已知点C为线段AB的中点,点D在线段BC上,且AD=7,BD=5,求线段CD的长。
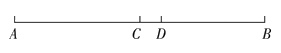
26. (6分)列方程或方程组解应用题:
为了防治“新型冠状病毒“,学校决定为师生购买一批医用口罩。已知甲种口罩每盒180元,乙种口罩每盒210元,学校购买了这两种口罩共50盒,合计花费9600元,求甲、乙两种口罩各购买了多少盒?
27. (6分)定义数对(x,y)经过一种运算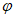 可以得到数对(x’,y’),并把该运算记作
可以得到数对(x’,y’),并把该运算记作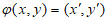 ,其中
,其中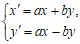 (a,b为常数)。例如,当
(a,b为常数)。例如,当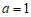 ,且
,且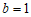 时,
时,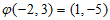 。
。
(1)当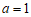 ,且
,且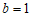 时,
时,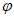 (0,1) =
(0,1) =
;
(2)若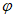 (1,2) = (0,4),则
(1,2) = (0,4),则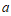 =
=
,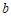 =
=
;
(3)如果组成数对(x,y)的两个数x,y满足二元一次方程2x–y=0,并且对任意数对(x,y)经过运算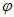 又得到数对(x,y),求a和b的值。
又得到数对(x,y),求a和b的值。
28. (6分)如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC = 2:1,将一直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方,将图1中的三角板绕点O按顺时针方向旋转一周。
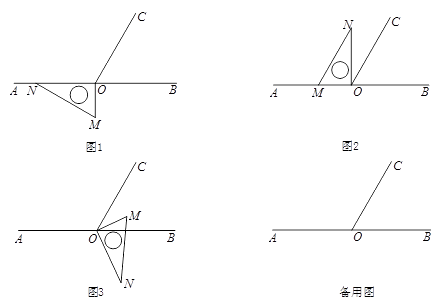
(1)三角板从图1位置旋转到图2位置(OM落在射线OA上), ON旋转的角度为
°;
(2)在三角板从图1旋转到图3位置的过程中,若三角板绕点O按每秒钟15°的速度旋转,当OM所在直线恰好平分∠BOC时,直接写出三角板绕点O运动的时间:
秒;
(3)在旋转过程中,请探究∠BON与∠COM的数量关系。(画出示意图,写出结论,并简要说明理由)
参考答案
一、选择题:本大题共12小题,每题2分,共24分。
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
答案 | D | D | B | A | D | C | B | C | D | B | B | C |
二、填空题:本大题共8小题,每题3分,共24分。
13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
答案不唯一 | 1 | 26 | 120 | 45或75 | -2 | -8 | ||
三、解答题:共52分。
21. (4分)-7
22. (每小题4分,共12分)
(1)x= (2) x=-4 (3)
23. (6分)
解: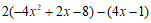
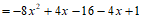
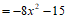 ,…………4分
,…………4分
当x=2时,原式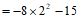
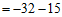
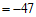 。 …………6分
。 …………6分
24. (6分)
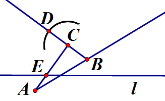 …………4分
…………4分
两点之间,线段最短 …………6分
25. (6分)
解:∵AD=7,BD=5
∴AB =AD+BD =7+5 =12 …………2分
∵C为线段AB的中点
∴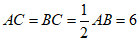 …………4分
…………4分
∴CD =AD–AC = 7-6 = 1
…………6分
26. (6分)
解法一:设购买甲种口罩x盒,则购买乙种口罩(50-x)盒,…………1分
由题意,得 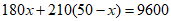 , ……………3分
, ……………3分
解得 x=30, ……4分
则 50-x=20。 ………5分
答:购买甲种口罩30盒,购买乙种口罩20盒。 ………6分
解法二:设购买甲种口罩x盒,购买乙种口罩y盒, ………1分
由题意,得 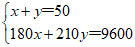 …………3分
…………3分
解得 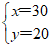 ………………5分
………………5分
答:购买甲种口罩30盒,购买乙种口罩20盒。 ……………6分
27. (6分)
(1)(1,-1) …………1分
(2)2,-1 …………3分
(3)a= ,b=…………6分
28. (6分)
(1)90; …………1分
(2)4秒或16秒; …………3分
(3)图略
当时,∠BON+∠COM=330° …………4分
当时,∠COM-∠BON=30°…………5分
当时,∠BON+∠COM=30°…………5分
当时,∠BON-∠COM =30°…………6分
