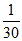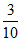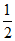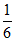本试卷共150分。考试时长120分钟。
第一部分(选择题
共40分)
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 已知集合A={x|x≥1},B={-1,0,1,2},则A∩B=
A. {2} B. {1,2} C. {0,1,2} D. {x|x≥-1}
2. 已知复数z满足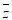 -z=2i,则z的虚部是
-z=2i,则z的虚部是
A. -1 B. 1 C. –i D. i
3. 在(x-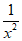 )6的展开式中,常数项为
)6的展开式中,常数项为
A. 15 B. -15 C. 30 D. -30
4. 某四棱锥的三视图如图所示,则该四棱锥的表面积为
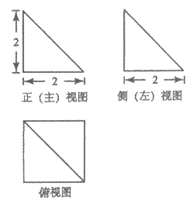
A. 12 B. 8+ C. 16 D. 8+4
C. 16 D. 8+4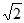
5. 已知函数f(x)=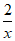 -log2x,则不等式f(x)>0的解集是
-log2x,则不等式f(x)>0的解集是
A. (0,1) B. (-∞,2) C. (2,+∞) D. (0,2)
6. 在△ABC中,C=90°,AC=4,BC=3,点P是AB的中点,则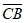 ·
·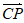 =
=
A. 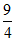 B. 4 C.
B. 4 C. 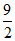 D. 6
D. 6
7. 在△ABC中,C=60°,a+2b=8,sinA=6sinB,则c=
A. 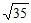 B.
B. 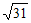 C. 6 D. 5
C. 6 D. 5
8. 抛物线具有以下光学性质:从焦点出发的光线经抛物线反射后平行于抛物线的对称轴。该性质在实际生产中应用非常广泛。如图,从抛物线y2=4x的焦点F发出的两条光线a,b分别经抛物线上的A,B两点反射,已知两条入射光线与x轴所成锐角均为60°,则两条反射光线a’和b’之间的距离为
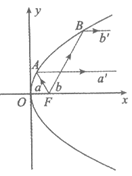
A. 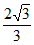 B.
B. 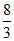 C.
C. 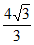 D.
D. 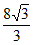
9. 在无穷等差数列{an}中,记Tn=a1-a2+a3-a4+a5-…+(-1)n+1an(n=1,2,…),则“存在m∈N*,使得Tm<Tm+2“是“{an}为递增数列“的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
10. 若非空实数集X中存在最大元素M和最小元素m,则记△(X)=M-m。下列命题中正确的是
A. 已知X={-1,1},Y={0,b},且△(X)=△(Y),则b=2
B. 已知X=[a,a+2],Y={y|y=x2,x∈X},则存在实数a,使得△(Y)<1
C. 已知X={x|f(x)≥g(x),x∈[-1,1]},若△(X)=2,则对任意x∈[-1,1],都有f(x)≥g(x)
D. 已知X=[a,a+2],Y=[b,b+3],则对任意的实数a,总存在实数b,使得△(X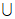 Y)≤3
Y)≤3
第二部分(非选择题
共110分)
二、填空题共5小题,每小题5分,共25分。
11. 函数f(x)=lnx+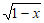 的定义域是________。
的定义域是________。
12. 已知双曲线C: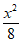 –
–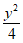 =1,则C的渐近线方程是________;过C的左焦点且与x轴垂直的直线交其渐近线于M,N两点,O为坐标原点,则△OMN的面积是________。
=1,则C的渐近线方程是________;过C的左焦点且与x轴垂直的直线交其渐近线于M,N两点,O为坐标原点,则△OMN的面积是________。
13. 在等比数列{an}中,a1+a3=10,a2+a4=-5,则公比q=________;若an>1,则n的最大值为________。
14. 已知函数f(x)=sinx,若对任意x∈R都有f(x)+f(x+m)=c(c为常数),则常数m的一个取值为________。
15. 长江流域水库群的修建和联合调度,极大地降低了洪涝灾害风险,发挥了重要的防洪减灾效益。每年洪水来临之际,为保证防洪需要、降低防洪风险,水利部门需要在原有蓄水量的基础上联合调度,统一蓄水,用蓄满指数(蓄满指数= )来衡量每座水库的水位情况。假设某次联合调度要求如下:
)来衡量每座水库的水位情况。假设某次联合调度要求如下:
(i)调度后每座水库的蓄满指数仍属于区间[0,100];
(ii)调度后每座水库的蓄满指数都不能降低;
(ⅲ)调度前后,各水库之间的蓄满指数排名不变。
记x为调度前某水库的蓄满指数,y为调度后该水库的蓄满指数,给出下面四个y关于x的函数解析式:
①y=–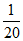 x2+6x;②y=10
x2+6x;②y=10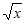 ;③y=10
;③y=10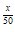 ;④y=100sin
;④y=100sin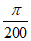 x。
x。
则满足此次联合调度要求的函数解析式的序号是________。
三、解答题共6小题,共85分。解答应写出文字说明,演算步骤或证明过程。
16. (本小题13分)
如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点。
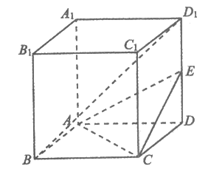
(I)求证:BD1∥平面ACE;
(Ⅱ)求直线AD与平面ACE所成角的正弦值。
17. (本小题13分)
已知函数f(x)=Asin(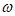 x+
x+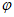 )(A>0,
)(A>0,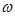 >0,|
>0,|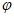 |<
|<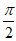 ),且f(x)图象的相邻两条对称轴之间的距离为
),且f(x)图象的相邻两条对称轴之间的距离为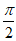 ,再从条件①、条件②、条件③中选择两个作为一组已知条件。
,再从条件①、条件②、条件③中选择两个作为一组已知条件。
(I)确定f(x)的解析式;
(Ⅱ)若f(x)图象的对称轴只有一条落在区间[0,a]上,求a的取值范围。
条件①:f(x)的最小值为-2;
条件②:f(x)图象的一个对称中心为(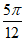 ,0);
,0);
条件③:f(x)的图象经过点(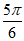 ,-1)。
,-1)。
注:如果选择多组条件分别解答,按第一个解答计分。
18.(本小题14分)
天文学上用星等表示星体亮度,星等的数值越小,星体越亮。视星等是指观测者用肉眼所看到的星体亮度;绝对星等是假定把恒星放在距地球32.6光年的地方测得的恒星的亮度,反映恒星的真实发光本领。
下表列出了(除太阳外)视星等数值最小的10颗最亮恒星的相关数据,其中a∈[0,1.3]。
星名 | 天狼星 | 老人星 | 南门二 | 大角星 | 织女一 | 五车二 | 参宿七 | 南河三 | 水委一 | 参宿四* |
视星等 | -1.47 | -0.72 | -0.27 | -0.04 | 0.03 | 0.08 | 0.12 | 0.38 | 0.46 | a |
绝对星等 | 1.42 | -5.53 | 4.4 | -0.38 | 0.6 | 0.1 | -6.98 | 2.67 | -2.78 | -5.85 |
赤纬 | -16.7° | -52.7° | -60.8° | 19.2° | 38.8° | 46° | -8.2° | 5.2° | -57.2° | 7.4° |
(I)从表中随机选择一颗恒星,求它的绝对星等的数值小于视星等的数值的概率;
(Ⅱ)已知北京的纬度是北纬40°,当且仅当一颗恒星的“赤纬“数值大于-50°时,能在北京的夜空中看到它。现从这10颗恒星中随机选择4颗,记其中能在北京的夜空中看到的数量为X颗,求X的分布列和数学期望;
(Ⅲ)记a=0时10颗恒星的视星等的方差为s12,记a=1.3时10颗恒星的视星等的方差为s22,判断s12与s22之间的大小关系。(结论不需要证明)
19. (本小题15分)
已知函数f(x)=ex(lnx-a)。
(I)若a=1,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若a>1,求证:函数f(x)存在极小值;
(Ⅲ)若对任意的实数x∈[1,+∞),f(x)≥-1恒成立,求实数a的取值范围。
20.(本小题15分)
已知椭圆C: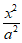 +
+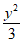 =1(a>0)的焦点在x轴上,且经过点E(1,
=1(a>0)的焦点在x轴上,且经过点E(1,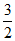 ),左顶点为D,右焦点为F。
),左顶点为D,右焦点为F。
(I)求椭圆C的离心率和△DEF的面积;
(Ⅱ)已知直线y=kx+1与椭圆C交于A,B两点。过点B作直线y=t(t>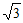 )的垂线,垂足为G。判断是否存在常数t,使得直线AG经过y轴上的定点?若存在,求t的值;若不存在,请说明理由。
)的垂线,垂足为G。判断是否存在常数t,使得直线AG经过y轴上的定点?若存在,求t的值;若不存在,请说明理由。
21.(本小题15分)
已知数列A:a1,a2,…,aN(N≥3)的各项均为正整数,设集合T={x|x=aj-ai,1≤i<j≤N},记T的元素个数为P(T)。
(I)若数列A:1,2,4,3,求集合T,并写出P(T)的值;
(Ⅱ)若A是递增数列,求证:“P(T)=N-1″的充要条件是“A为等差数列“;
(Ⅲ)若N=2n+1,数列A由1,2,3,…,n,2n这n+1个数组成,且这n+1个数在数列A中每个至少出现一次,求P(T)的取值个数。
参考答案
一、选择题(共10小题,每小题4分,共40分)
1. B 2. A 3. A 4. D 5. D 6. C 7. B 8. C 9. B 10. D
二、填空题(共5小题,每小题5分,共25分)
11. (0,1] 12. y=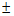
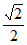 x,6
x,6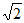
13. –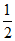 ,3 14. π(答案不唯一,只要是(2k+1)π即可)
,3 14. π(答案不唯一,只要是(2k+1)π即可)
15. ②④
注:第(12)和(13)题第一空3分,第二空2分。第(15)题全部选对得5分,不选或有错选得0分,其他得3分。
三、解答题(共6小题,共85分)
16.(共13分)
解:(I)连接BD交AC于点O,连接OE,
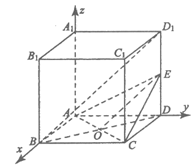
在正方形ABCD中,OB=OD。
因为E为DD1的中点,
所以OE∥BD1 3分
因为BD1 平面ACE,OE
平面ACE,OE 平面ACE,
平面ACE,
所以BD1∥平面ACE。 5分
(Ⅱ)不妨设正方体的棱长为2,建立如图所示的空间直角坐标系A-xyz。
则A(0,0,0),C(2,2,0),D(0,2,0),E(0,2,1),
所以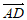 =(0,2,0),
=(0,2,0),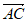 =(2,2,0),
=(2,2,0),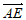 =(0,2,1)。 8分
=(0,2,1)。 8分
设平面ACE的法向量为n=(x,y,z),
所以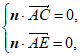 所以
所以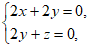 即
即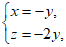 10分
10分
令y=-1,则x=1,z=2,
于是n=(1,-1,2)。 1分
设直线AD与平面ACE所成角为θ,
则sinθ=|cos<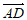 ,n>|=
,n>|=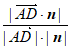 =
=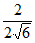 =
=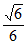 。 13分
。 13分
所以直线AD与平面ACE所成角的正弦值为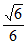 。
。
17. (共13分)
解:(I)由于函数f(x)图象上两相邻对称轴之间的距离为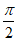 ,
,
所以f(x)的最小正周期T=2×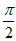 =
=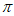 ,
,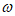 =
=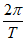 =2。 2分
=2。 2分
此时f(x)=Asin(2x+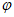 )。
)。
选条件①②:
因为f(x)的最小值为-A,所以A=2。 3分
因为f(x)图象的一个对称中心为(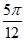 ,0),
,0),
所以2×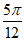 +
+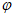 =k
=k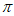 (k∈Z), 5分
(k∈Z), 5分
所以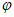 =k
=k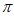 –
–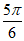 (k∈Z),
(k∈Z),
因为|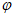 |<
|<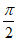 ,所以
,所以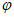 =
=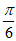 ,此时k=1 7分
,此时k=1 7分
所以f(x)=2sin(2x+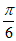 )。 8分
)。 8分
选条件①③:
因为f(x)的最小值为-A,所以A=2 3分
因为函数f(x)的图象过点(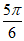 ,-1),
,-1),
则f(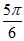 )=-1,即2sin(
)=-1,即2sin(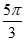 +
+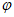 )=-1,sin(
)=-1,sin(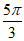 +
+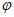 )=–
)=–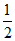 。
。
因为|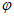 |<
|<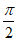 ,所以
,所以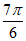 <
<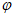 +
+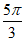 <
<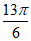 , 5分
, 5分
所以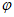 +
+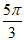 =
=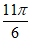 ,
,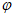 =
=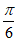 。 7分
。 7分
所以f(x)=2sin(2x+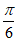 )。 8分
)。 8分
选条件②③:
因为函数f(x)的一个对称中心为(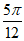 ,0),
,0),
所以2×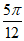 +
+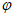 =kπ(k∈Z), 4分
=kπ(k∈Z), 4分
所以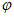 =kπ-
=kπ-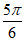 (k∈Z)。
(k∈Z)。
因为|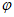 |<
|<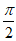 ,所以
,所以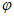 =
=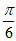 ,此时k=1。 6分
,此时k=1。 6分
所以f(x)=Asin(2x+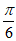 )。
)。
因为函数f(x)的图象过点(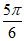 ,-1),
,-1),
所以f(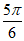 )=-1,即Asin(
)=-1,即Asin(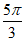 +
+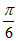 )=-1,Asin
)=-1,Asin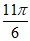 =-1,
=-1,
所以A=2。 7分
所以f(x)=2sin(2x+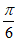 )。 8分
)。 8分
(Ⅱ)因为x∈[0,a],所以2x+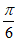 ∈[
∈[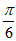 ,2a+
,2a+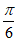 ],
],
因为f(x)图象的对称轴只有一条落在区间[0,a]上,
所以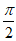 ≤2a+
≤2a+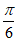 <
<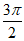 , 11分
, 11分
得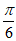 ≤a<
≤a<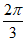 , 13分
, 13分
所以a的取值范围为[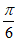 ,
,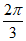 ]。
]。
18.(共14分)
解:(I)设一颗星的绝对星等的数值小于视星等的数值为事件A。由图表可知,10颗恒星有5颗恒星绝对星等的数值小于视星等的数值。
所以P(A)=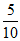 =
=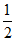 。 3分
。 3分
(Ⅱ)由图表知,有7颗恒星的“赤纬“数值大于-50°,有3颗恒星的“赤纬“数值小于-50°。所以随机变量X的所有可能取值为:1,2,3,4。 4分
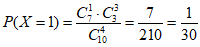 ,
,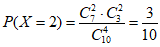 ,
,
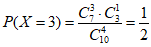 ,
,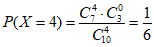 。 8分
。 8分
所以随机变量X的分布列为:
X | 1 | 2 | 3 | 4 |
P |
|
|
|
|
9分
所以E(X)=1×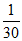 +2×
+2×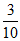 +3×
+3×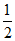 +4×
+4×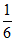 =
=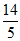 。 11分
。 11分
(Ⅲ)s12<s22。 14分
19. (共15分)
解:(1)当a=1时,f(x)=ex(lnx-1),
所以f’(x)=ex(lnx-1)+ex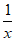 =ex(lnx+
=ex(lnx+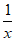 -1)。 1分
-1)。 1分
所以f(1)=-e,f’(1)=0。 3分
曲线y=f(x)在点(1,f(1))处的切线方程为y=-e。 4分
(Ⅱ)由f(x)=ex(lnx-a),得f’(x)=ex(lnx+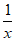 -a),
-a),
令h(x)=lnx+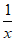 -a,则h’(x)=
-a,则h’(x)=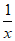 –
–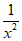 =
=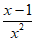 。 6分
。 6分
当0<x<1时,h’(x)<0,当x>1时,h’(x)>0,
所以h(x)在区间(0,1)上是减函数,在区间(1,+∞)上是增函数。
所以h(x)的最小值为h(1)=1-a。 7分
当a>1时,h(1)=1-a<0,h(ea)=e-a>0, 9分
又h(x)在(1,+∞)单调递增,
故存在x0∈(1,ea),使得h(x0)=0,在区间(1,x0)上h(x)<0,在区间(x0,+∞)上h(x)>0。 10分
所以,在区间(1,x0)上f’(x)<0,在区间(x0,+∞)上f’(x)>0,
所以,在区间(1,x0)上f(x)单调递减,在区间(x0,+∞)上f(x)单调递增,故函数f(x)存在极小值。 11分
(Ⅲ)对任意的实数x∈[1,+∞),f(x)≥-1恒成立,等价于f(x)的最小值大于或等于-1。
①当a≤1时,h(1)=1-a≥0,由(Ⅱ)得h(x)≥0,所以f’(x)≥0。
所以f(x)在[1,+∞)上单调递增,
所以f(x)的最小值为f(1)=-ae。
由-ae≥-1,得a≤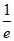 ,满足题意。 13分
,满足题意。 13分
②当a>1时,由(Ⅱ)知,f(x)在(1,x0)上单调递减,
所以在(1,x0)上f(x)≤f(1)=-ae<-e,不满足题意。
综上所述,实数a的取值范围是(-∞,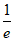 ]。 15分
]。 15分
20.(共15分)
解:(I)依题意,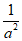 +
+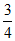 =1,解得a=2。 1分
=1,解得a=2。 1分
因为c2=a2-b2=4-3=1,即c=1, 2分
所以D(-2,0),F(1,0),
所以离心率e=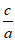 =
=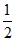 ,△DEF的面积S=
,△DEF的面积S=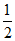 ×3×
×3×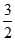 =
=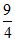 。 5分
。 5分
(Ⅱ)由已知,直线DE的方程为y=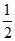 x+1。
x+1。
当A(-2,0),B(1,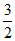 ),G(1,t)时,
),G(1,t)时,
直线AG的方程为y=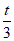 (x+2),交y轴于点(0,
(x+2),交y轴于点(0,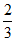 t);
t);
当A(1,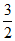 ),B(-2,0),G(-2,t)时,
),B(-2,0),G(-2,t)时,
直线AG的方程为y-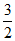 =
=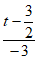 (x-1),交y轴于点(0,
(x-1),交y轴于点(0,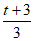 )。
)。
若直线AG经过y轴上定点,则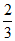 t=
t=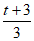 ,
,
即t=3,直线AG交y轴于点(0,2) 7分
下面证明存在实数t=3,使得直线AG经过y轴上定点(0,2)。
联立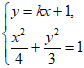 消y整理,得(4k2+3)x2+8kx-8=0, 8分
消y整理,得(4k2+3)x2+8kx-8=0, 8分
设A(x1,y1),B(x2,y2)。
则x1+x2=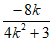 ,x1x2=
,x1x2=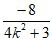 。 10分
。 10分
设点G(x2,3),所以直线AG的方程y-3=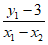 (x-x2)。 11分
(x-x2)。 11分
令x=0,得y=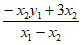 +3=
+3=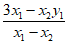
=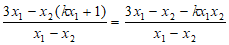 12分
12分
因为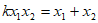 ,
,
所以y=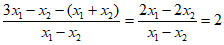
所以直线AG过定点(0,2)
综上,存在实数t=3,使得直线AG经过y轴上定点(0,2) 15分
21.(共15分)
解:(I)因为a1=1,a2=2,a3=4,a4=3,
所以T={1,2,3,-1},P(T)=4 4分
(Ⅱ)充分性:若A是等差数列,设公差为d。
因为数列A是递增数列,所以d>0。
则当j>i时,aj-ai=(j-i)d。
所以T={d,2d,…,(N-1)d},P(T)=N-1。 6分
必要性:若P(T)=N-1。
因为A是递增数列,所以a2-a1<a3-a1<…<aN-a1,
所以a2-a1,a3-a1,…,aN-a1∈T,且互不相等。
所以T={a2-a1,a3-a1,…,aN-a1}。
又a3-a2<a4-a2<…<aN-1-a2<aN-a2<aN-a1,
所以a3-a2,a4-a2,…,aN-a2,aN-a1∈T,且互不相等。
所以a3-a2=a2-a1,a4-a2=a3-a1,…,aN-a2=aN-1-a1。
所以a2-a1=a3-a2=…=aN-aN-1,
所以A为等差数列。 9分
(Ⅲ)因为数列A由1,2,3,…,n,2n这n+1个数组成,任意两个不同的数作差,
差值只可能为±1,±2,±3,…,±(n-1)和±(2n-1),±(2n-2),…,±n。
共2(n-1)+2n=4n-2个不同的值;且对任意的m=1,2,3,…,n-1,n,…,2n-1,m和-m这两个数中至少有一个在集合T中。 11分
又因为1,2,3,…,n,2n这n+1个数在数列A中共出现N=2n+1次,所以数列A中存在ai=aj(i≠j),所以0∈T。
综上,P(T)≤4n-1,且P(T)≥2n。 12分
设数列A0:1,1,2,2,3,3,4,4,…,n,n,2n,此时T={0,1,2,…,2n-1},P(T)=2n。
现对数列A0分别作如下变换:
把一个1移动到2,3之间,得到数列:1,2,2,1,3,3,4,4,…,n,n,2n,
此时T={0,1,2,3…,(2n-1),-1},P(T)=2n+1。
把一个1移动到3,4之间,得到数列:1,2,2,3,3,1,4,4,…,n,n,2n,
此时T={0,1,2,3,…,(2n-1),-1,-2},P(T)=2n+2。
……
把一个1移动到n-1,n之间,得到数列:1,2,2,3,3,4,4,…,n-1,n-1,1,n,n,2n,
此时T={0,1,2,3,…,(2n-1),-1,-2,…,2-n},P(T)=2n+n-2=3n-2。
把一个1移动到n,2n之间,得到数列:1,2,2,3,3,4,4,…,n,n,1,2n,
此时T={0,1,2,3,…,2n-1,-1,-2,…,1-n},P(T)=2n+n-1=3n-1。
再对数列A0依次作如下变换:
把一个1移为2n的后一项,得到数列A1:1,2,2,3,3,4,4,…,n,n,2n,1,
此时T={0,1,2,3,…,2n-1,-1,-2,…,1-n,1-2n},P(T)=3n;
再把一个2移为2n的后一项:得到数列A2:1,2,3,3,4,4;…,n,n,2n,2,1,
此时T={0,1,2,3,…,2n-1,-1,-2,…,1-n,1-2n,2-2n},P(T)=3n+1;
依此类推……
最后把一个n移为2n的后一项:得到数列An:1,2,3,4,…,n,2n,n,n-1,…,2,1,
此时T=(0,1,2,3,…,2n-1,-1,-2,…,1-n,1-2n,2-2n,…,-n},P(T)=4n-1。
综上所述,P(T)可以取到从2n到4n-1的所有2n个整数值,所以P(T)的取值个数为2n。 15分