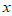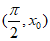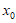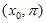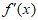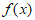本试卷共150分。考试时长120分钟。
第一部分(选择题
共40分)
一、选择题:共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 已知集合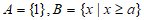 ,若
,若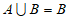 ,则实数a的取值范围是
,则实数a的取值范围是
A. 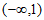 B.
B. 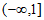 C.
C. 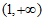 D.
D. 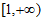
2. 如图,在复平面内,复数z对应的点为P,则复数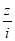 的虚部为
的虚部为
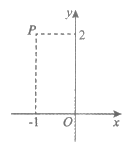
A. 1 B. -1 C. 2 D. -2
3. 已知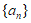 为等差数列,
为等差数列,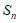 为其前n项和,若
为其前n项和,若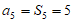 ,则
,则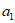 =
=
A. -5 B. -4 C. -3 D. -2
4. 在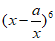 的展开式中,
的展开式中,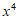 的系数为12,则a的值为
的系数为12,则a的值为
A. 2 B. -2 C. 1 D. -1
5. 函数①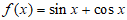 ,②
,②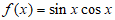 ,③
,③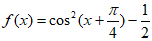 中,周期是
中,周期是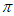 且为奇函数的所有函数的序号是
且为奇函数的所有函数的序号是
A. ①② B. ② C. ③ D. ②③
6. 已知函数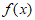 满足
满足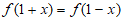 ,且当
,且当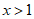 时,
时,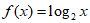 ,则
,则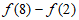 =
=
A. -2 B. -1 C. 1 D. 3
7. 已知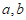 是单位向量,
是单位向量,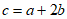 ,若a⊥c,则|c|=
,若a⊥c,则|c|=
A. 3 B. 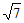 C.
C. 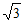 D.
D. 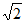
8. 已知点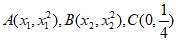 ,则”△ABC是等边三角形”是”直线AB的斜率为0“的
,则”△ABC是等边三角形”是”直线AB的斜率为0“的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
9. 设无穷等比数列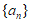 的前n项和为
的前n项和为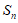 ,若
,若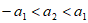 ,则
,则
A. 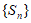 为递减数列 B.
为递减数列 B. 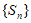 为递增数列
为递增数列
C. 数列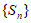 有最大项 D. 数列
有最大项 D. 数列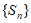 有最小项
有最小项
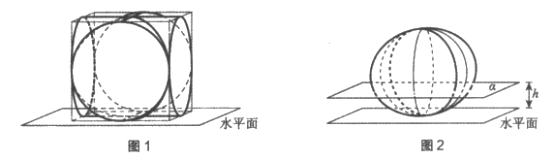
10. 我国魏晋时期的数学家刘徽创造了一个称为”牟合方盖”的立体图形来推算球的体积,如图1,在一个棱长为2a的立方体内作两个互相垂直的内切圆柱,其相交的部分就是牟合方盖,如图2,设平行于水平面且与水平面距离为h的平面为α,记平面α截牟合方盖所得截面的面积为S,则函数S=f(h)的图象是
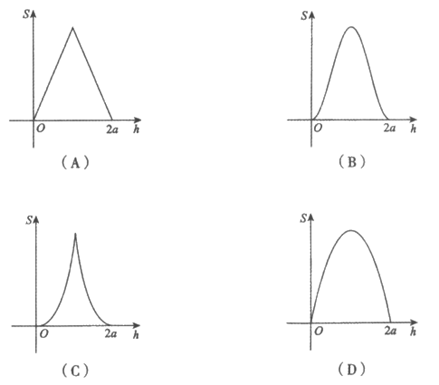
第二部分(非选择题
共110分)
二、填空题:共5小题,每小题5分,共25分。
11. 已知函数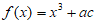 ,若曲线
,若曲线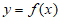 在点
在点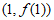 处的切线的斜率为2,则实数a的值是___________。
处的切线的斜率为2,则实数a的值是___________。
12. 已知双曲线的两条渐近线互相垂直,则该双曲线的离心率为____________。
13. 已知点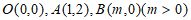 ,则
,则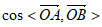 =__________;若B是以OA为边的矩形的顶点,则m=___________。
=__________;若B是以OA为边的矩形的顶点,则m=___________。
14. 若实数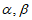 满足方程组
满足方程组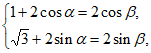 则
则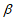 的一个值是___________。
的一个值是___________。
15. 对平面直角坐标系xOy中的两组点,如果存在一条直线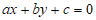 使这两组点分别位于该直线的两侧,则称该直线为”分类直线”,对于一条分类直线
使这两组点分别位于该直线的两侧,则称该直线为”分类直线”,对于一条分类直线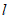 ,记所有的点到
,记所有的点到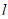 的距离的最小值为
的距离的最小值为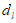 ,约定:
,约定: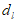 越大,分类直线
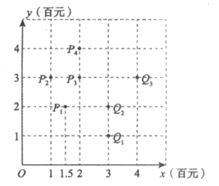
越大,分类直线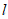 的分类效果越好。某学校高三(2)班的7位同学在2020年期间网购文具的费用x(单位:百元)和网购图书的费用y(单位:百元)的情况如图所示。现将P1,P2,P3和P4归为第Ⅰ组点,将Q1,Q2和Q3归为第Ⅱ组点,在上述约定下,可得这两组点的分类效果最好的分类直线,记为L。给出下列四个结论:
的分类效果越好。某学校高三(2)班的7位同学在2020年期间网购文具的费用x(单位:百元)和网购图书的费用y(单位:百元)的情况如图所示。现将P1,P2,P3和P4归为第Ⅰ组点,将Q1,Q2和Q3归为第Ⅱ组点,在上述约定下,可得这两组点的分类效果最好的分类直线,记为L。给出下列四个结论:
①直线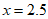 比直线
比直线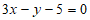 的分类效果好;
的分类效果好;
②分类直线L的斜率为2;
③该班另一位同学小明的网购文具与网购图书的费用均为300元,则小明的这两项网购花销的费用所对应的点与第Ⅱ组点位于L的同侧;
④如果从第Ⅰ组点中去掉点P1,第Ⅱ组点保持不变,则分类效果最好的分类直线不是L。
其中所有正确结论的序号是____________。
三、解答题:共6小题,共85分。解答应写出文字说明、演算步骤或证明过程。
16.(本小题共14分)
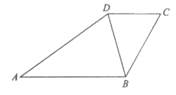
如图,在四边形ABCD中,AB∥CD,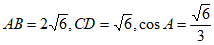 ,
,
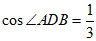 。
。
(Ⅰ)求cos∠BDC;
(Ⅱ)求BC的长。
17.(本小题共14分)
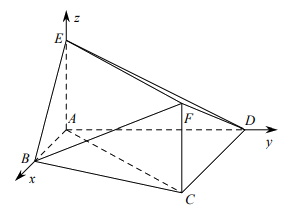
在如图所示的多面体中,AB∥CD,四边形ACFE为矩形,AB=AE=1,AD=CD=2。
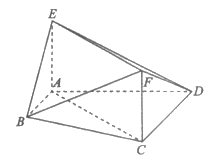
(Ⅰ)求证:平面ABE∥平面CDF;
(Ⅱ)设平面BEF∩平面CDF=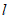 ,再从条件①、条件②、条件③这三个条件中选择若干个作为已知,使二面角
,再从条件①、条件②、条件③这三个条件中选择若干个作为已知,使二面角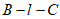 的大小确定,并求此二面角的余弦值。
的大小确定,并求此二面角的余弦值。
条件①:AB⊥AD;
条件②:AE⊥平面ABCD;
条件③:平面AED⊥平面ABCD。
18.(本小题共14分)
每年的4月23日是联合国教科文组织确定的”世界读书日”,又称”世界图书和版权日”。为了解某地区高一学生阅读时间的分配情况,从该地区随机抽取了500名高一学生进行在线调查,得到了这500名学生的日平均阅读时间(单位:小时),并将样本数据分成[0,2],(2,4],(4,6],(6,8],(8,10],(10,12],(12,14],(14,16],(16,18]九组,绘制成如图所示的频率分布直方图。
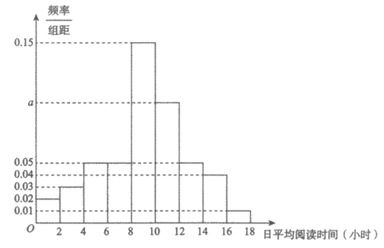
(Ⅰ)求a的值;
(Ⅱ)为进一步了解这500名学生数字媒体阅读时间和纸质图书阅读时间的分配情况,从日平均阅读时间在(12,14],(14,16],(16,18]三组内的学生中,采用分层抽样的方法抽取了10人,现从这10人中随机抽取3人,记日平均阅读时间在(14,16]内的学生人数为X,求X的分布列;
(Ⅲ)以调查结果的频率估计概率,从该地区所有高一学生中随机抽取20名学生,用”P20(k)”表示这20名学生中恰有k名学生日平均阅读时间在(10,12](单位:小时)内的概率,其中k=0,1,2,…,20。当P20(k)最大时,写出k的值。(只需写出结论)
19.(本小题共15分)
已知函数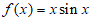 。
。
(Ⅰ)判断函数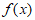 在区间
在区间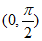 上的单调性,并说明理由;
上的单调性,并说明理由;
(Ⅱ)求证:函数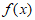 在
在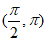 内有且只有一个极值点;
内有且只有一个极值点;
(Ⅲ)求函数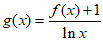 在区间
在区间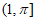 上的最小值。
上的最小值。
20.(本小题共14分)
已知椭圆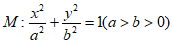 过
过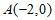 ,
,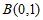 两点。
两点。
(Ⅰ)求椭圆M的离心率;
(Ⅱ)设椭圆M的右顶点为C,点P在椭圆M上(P不与椭圆M的顶点重合),直线AB与直线CP交于点Q,直线BP交x轴于点S,求证:直线SQ过定点。
21.(本小题共14分)
已知无穷数列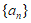 ,对于
,对于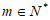 ,若
,若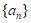 同时满足以下三个条件,则称数列
同时满足以下三个条件,则称数列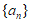 具有性质
具有性质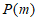 。
。
条件①: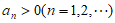 ;
;
条件②:存在常数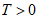 ,使得
,使得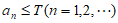 ;
;
条件③: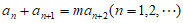 。
。
(Ⅰ)若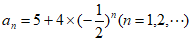 ,且数列
,且数列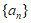 具有性质
具有性质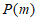 ,直接写出m的值和一个T的值;
,直接写出m的值和一个T的值;
(Ⅱ)是否存在具有性质P(1)的数列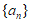 ?若存在,求数列
?若存在,求数列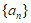 的通项公式;若不存在,说明理由;
的通项公式;若不存在,说明理由;
(Ⅲ)设数列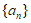 具有性质
具有性质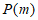 ,且各项均为正整数,求数列
,且各项均为正整数,求数列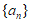 的通项公式。
的通项公式。
【试题答案】
1. 评分参考中所注分数,表示考生正确做到此步应得的累加分数。
2. 其它正确解法可以参照评分标准按相应步骤给分。
一、选择题:共10小题,每小题4分,共40分。
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | B | A | C | B | D | C | C | A | D | D |
二、填空题:共5小题,每小题5分,共25分。
11. -1 12. 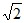 13.
13. 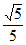 5
5
14. 0,答案不唯一,满足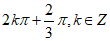 或
或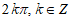 即可
即可
15. ②③④
三、解答题:共6小题,共85分。
16.(本小题共14分)
解:(Ⅰ)在△ABD中,因为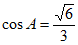 ,cos∠ADB=
,cos∠ADB=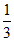 ,
,
所以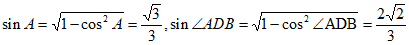 ,
,
所以cos∠ABD=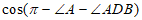
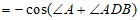
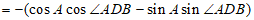
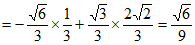 。
。
因为AB∥CD,
所以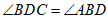 ,
,
所以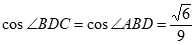 。
。
(Ⅱ)在△ABD中,由正弦定理得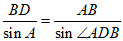 。
。
因为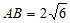 ,
,
所以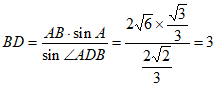 。
。
因为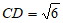 ,
,
在△CBD中,由余弦定理得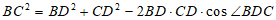

=11。
所以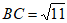 。
。
17.(本小题共14分)
解:(Ⅰ)因为四边形ACFE为矩形,
所以CF∥AE。
又因为AB∥CD,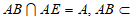 平面ABE,AE
平面ABE,AE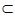 平面ABE,CD
平面ABE,CD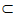 平面CDF,CF
平面CDF,CF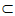 平面CDF,
平面CDF,
所以,平面ABE∥平面CDF。
(Ⅱ)选择①②,或①②③
因为AE⊥平面ABCD,AB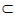 平面ABCD,AD
平面ABCD,AD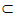 平面ABCD,
平面ABCD,
所以AE⊥AB,AE⊥AD。
又因为AB⊥AD,
所以,分别以AB,AD,AE所在的直线为x轴,y轴,z轴建立如图所示的空间直角坐标系,由题意得
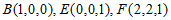 ,
,
所以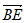 =
=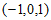 ,
,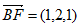 。
。
设平面BEF的法向量为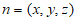 ,则
,则
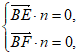 即
即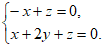
令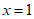 ,则
,则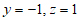 ,
,
于是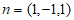 。
。
由(Ⅰ)可得:AD⊥平面CDF,
取平面CDF的一个法向量为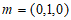 ,
,
所以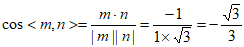 ,
,
所以,二面角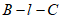 的余弦值为
的余弦值为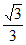 ,
,
选择①③
因为
平面AED⊥平面ABCD,平面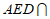 平面ABCD=AD,
平面ABCD=AD,
AB⊥AD,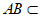 平面ABCD,
平面ABCD,
所以 AB⊥平面AED。
又因为
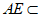 平面AED,
平面AED,
所以 AB⊥AE。
在矩形ACFE中,AE⊥AC,
因为
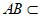 平面ABCD,
平面ABCD,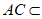 平面ABCD,
平面ABCD,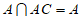 ,
,
所以 AE⊥平面ABCD。
又因为
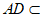 平面ABCD,
平面ABCD,
所以 AE⊥AD。
分别以AB,AD,AE所在的直线为x轴,y轴,z轴建立如图所示的空间直角坐标系,由题意得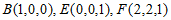 ,
,
所以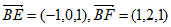 ,
,
设平面BEF的法向量为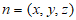 ,则
,则
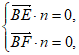 即
即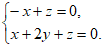
令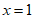 ,则
,则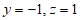 ,
,
于是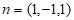 。
。
由(Ⅰ)可得:AD⊥平面CDF,
取平面CDF的一个法向量为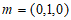 ,
,
所以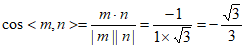 ,
,
所以
二面角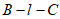 的余弦值为
的余弦值为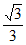 。
。
18.(本小题共14分)
解:(Ⅰ)由频率分布直方图可得:
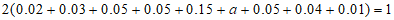
解得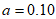 。
。
(Ⅱ)由频率分布直方图可知,这500名学生中日平均阅读时间在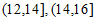 ,
,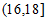 三组内的学生人数分别为
三组内的学生人数分别为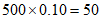 人,
人,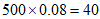 人,
人,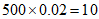 人。
人。
若采用分层抽样的方法抽取了10人,则从日平均阅读时间在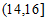 内的学生中抽取了
内的学生中抽取了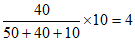 人。
人。
现从这10人中随机抽取3人,则X的可能取值为0,1,2,3。
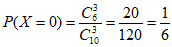 ,
,
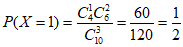 ,
,
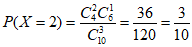 ,
,
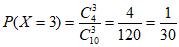 。
。
所以X的分布列为
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
(Ⅲ)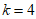 。
。
19.(本小题共15分)
解:(Ⅰ)由题意知,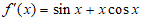 ,
,
因为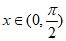 ,
,
所以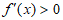 ,
,
所以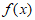 在
在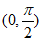 上单调递增。
上单调递增。
(Ⅱ)设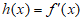 ,则
,则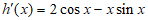 ,
,
当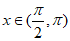 时,
时,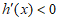 ,
,
所以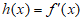 在
在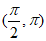 内单调递减。
内单调递减。
又因为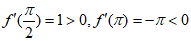 ,
,
所以,存在唯一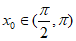 ,使得
,使得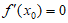 ,
,
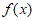 与
与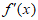 在区间
在区间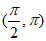 上的情况如下:
上的情况如下:
|
|
|
|
| + | 0 | - |
| ↗ | 极大值 | ↘ |
所以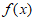 在
在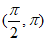 内有且只有一个极值点。
内有且只有一个极值点。
(Ⅲ)由(Ⅰ)(Ⅱ)可知,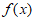 在
在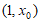 内单调递增,在
内单调递增,在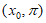 内单调递减。
内单调递减。
又因为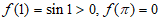 ,
,
所以,当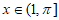 时,
时,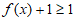 。
。
又因为,当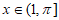 时,
时,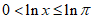 ,
,
所以
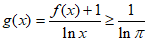 ,当且仅当
,当且仅当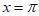 时等号成立,
时等号成立,
所以
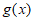 在
在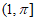 上的最小值为
上的最小值为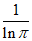 。
。
20.(本小题共14分)
解:(Ⅰ)因为
点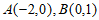 都在椭圆M上,
都在椭圆M上,
所以
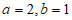 ,
,
所以
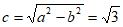 ,
,
所以
椭圆M的离心率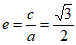 。
。
(Ⅱ)方法一:
由(Ⅰ)知椭圆M的方程为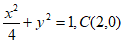 ,
,
由题意知:直线AB的方程为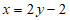 ,
,
设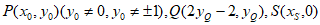 ,
,
因为
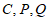 三点共线,所以有
三点共线,所以有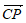 ∥
∥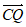 ,
,
所以 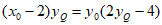 ,
,
所以 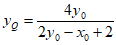 ,
,
所以 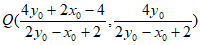 。
。
因为 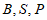 三点共线,
三点共线,
所以 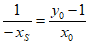 ,即
,即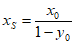 ,
,
所以 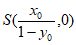 ,
,
所以
直线QS的方程为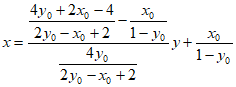 ,
,
即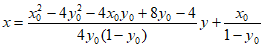 。
。
又因为
点P在椭圆M上,所以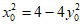 ,
,
所以
直线QS的方程为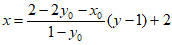 ,
,
所以
直线QS过定点(2,1)。
方法二:
直线QS过定点T(2,1),理由如下:
设直线BP为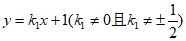 ,直线CP为
,直线CP为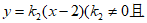
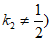 。
。
所以
直线BP与x轴的交点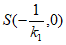 。
。
因为
直线AB的方程为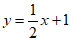 ,
,
所以
直线CP与直线AB的交点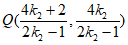 ,
,
所以
直线TS的斜率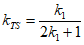 ,直线TQ的斜率
,直线TQ的斜率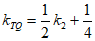 ,
,
所以
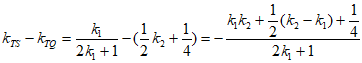 。
。
将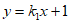 代入方程
代入方程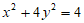 得
得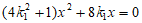 ,
,
所以
点P的横坐标为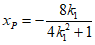 ,则
,则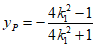 。
。
将点P的坐标代入直线CP的方程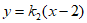 ,整理得
,整理得
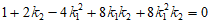 ,
,
所以
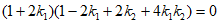 。
。
因为
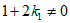 ,所以
,所以
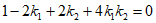 ,
,
所以
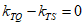 ,
,
所以
直线QS过定点T(2,1)。
21.(本小题共14分)
解:(Ⅰ)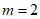 ;
;
答案不唯一,如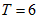 。
。
(Ⅱ)不存在具有性质P(1)的数列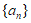 ,理由如下:
,理由如下:
假设存在具有性质P(1)的数列,设为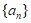 ,则
,则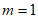 ,
,
所以
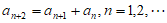 。
。
因为
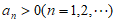 ,
,
所以
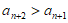 ,即
,即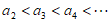 ,
,
所以
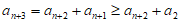 ,即
,即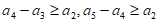 ,…,
,…,
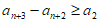 。
。
累加得,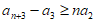 ,
,
对于常数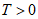 ,当
,当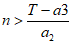 时,
时,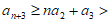 T,与②矛盾,
T,与②矛盾,
所以
不存在具有性质P(1)的数列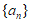 。
。
(Ⅲ)因为数列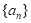 具有性质
具有性质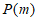 ,由(Ⅱ)知
,由(Ⅱ)知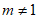 。
。
①当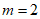 时,
时,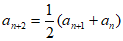 ,即
,即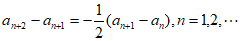 ,
,
所以
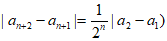 。
。
若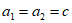 (c为常数,且
(c为常数,且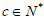 ),则
),则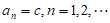 。
。
经检验,数列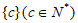 具有性质
具有性质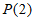 。
。
若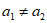 ,当
,当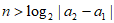 时,
时,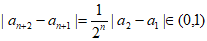 ,
,
与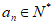 矛盾。
矛盾。
②当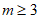 时,令
时,令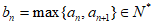 ,则
,则
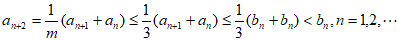 ,
,
所以
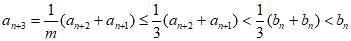 ,
,
所以
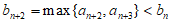 ,
,
所以
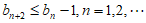 ,
,
所以
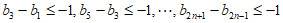 ,
,
所以
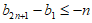 。
。
当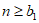 时,
时,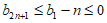 ,与
,与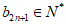 矛盾。
矛盾。
综上所述,数列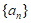 的通项公式为
的通项公式为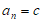 (c为常数,且
(c为常数,且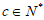 )。
)。