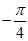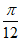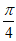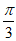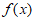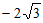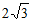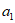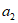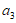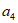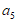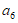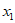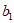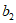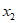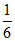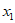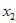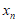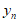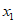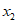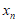本试卷共150分。考试时长120分钟。
第一部分(选择题
共40分)
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 已知集合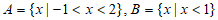 ,那么
,那么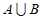 =
=
A. (-1,2) B. (-1,1) C. (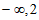 ) D.
) D. 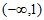
2. 在复平面内,复数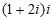 对应的点位于
对应的点位于
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3. 某中学高一、高二和高三各年级人数见下表,采用分层抽样的方法调查学生的健康状况,在抽取的样本中,高二年级有20人,那么该样本中高三年级的人数为
年级 | 人数 |
高一 | 550 |
高二 | 500 |
高三 | 450 |
合计 | 1500 |
A. 18 B. 22 C. 40 D. 60
4. 某四棱锥的三视图如图所示,该四棱锥的体积为
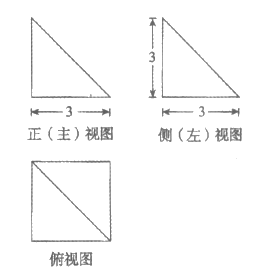
A. 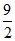 B. 9 C.
B. 9 C. 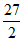 D. 27
D. 27
5. 已知圆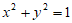 截直线
截直线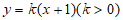 所得弦的长度为1,那么k的值为
所得弦的长度为1,那么k的值为
A. 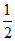 B.
B. 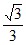 C. 1 D.
C. 1 D. 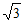
6. 已知函数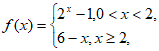 那么不等式
那么不等式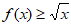 的解集为
的解集为
A. 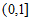 B.
B. 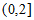 C.
C. 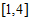 D.
D. 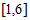
7. “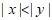 “是”
“是”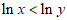 “成立的
“成立的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
8. 宽与长的比为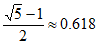 的矩形叫做黄金矩形,它广泛的出现在艺术、建筑、人体和自然界中,令人赏心悦目,在黄金矩形ABCD中,
的矩形叫做黄金矩形,它广泛的出现在艺术、建筑、人体和自然界中,令人赏心悦目,在黄金矩形ABCD中,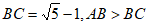 ,那么
,那么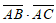 的值为
的值为
A. 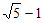 B.
B. 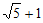 C. 4 D.
C. 4 D. 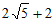
9. 已知椭圆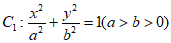 的右焦点F与抛物线
的右焦点F与抛物线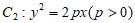 的焦点重合,P为椭圆C1与抛物线C2的公共点,且
的焦点重合,P为椭圆C1与抛物线C2的公共点,且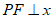 轴,那么椭圆C1的离心率为
轴,那么椭圆C1的离心率为
A. 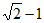 B.
B. 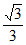 C.
C. 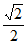 D.
D. 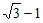
10. 如图,将线段AB,CD用一条连续不间断的曲线y=f(x)连接在一起,需满足要求:曲线y=f(x)经过点B,C,并且在点B,C处的切线分别为直线AB,CD,那么下列说法正确的是
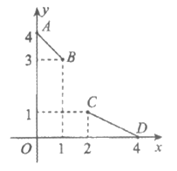
A. 存在曲线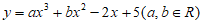 满足要求
满足要求
B. 存在曲线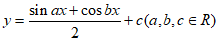 满足要求
满足要求
C. 若曲线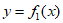 和
和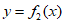 满足要求,则对任意满足要求的曲线
满足要求,则对任意满足要求的曲线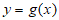 ,存在实数
,存在实数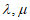 ,使得
,使得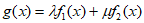
D. 若曲线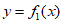 和
和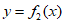 满足要求,则对任意实数
满足要求,则对任意实数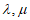 ,当
,当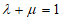 时,曲线
时,曲线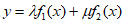 满足要求
满足要求
第二部分(非选择题
共110分)
二、填空题:共5小题,每小题5分,共25分。
11. 在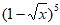 的展开式中,
的展开式中,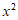 的系数为______________。(用数字作答)
的系数为______________。(用数字作答)
12. 已知双曲线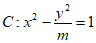 经过点
经过点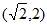 ,那么m的值为___________,C的渐近线方程为____________。
,那么m的值为___________,C的渐近线方程为____________。
13. 已知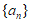 为等比数列,
为等比数列,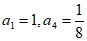 ,那么
,那么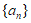 的公比为___________,数列
的公比为___________,数列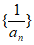 的前5项和为_____________。
的前5项和为_____________。
14. 已知函数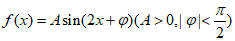 ,其中x和
,其中x和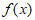 部分对应值如下表所示:
部分对应值如下表所示:
x |
| 0 |
|
|
|
| -2 |
| -2 | 2 |
|
那么A=__________________。
15. 设A是非空数集,若对任意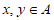 ,都有
,都有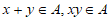 ,则称A具有性质P,给出以下命题:
,则称A具有性质P,给出以下命题:
①若A具有性质P,则A可以是有限集;
②若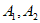 具有性质P,且
具有性质P,且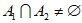 ,则
,则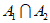 具有性质P;
具有性质P;
③若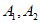 具有性质P,则
具有性质P,则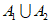 具有性质P;
具有性质P;
④若A具有性质P,且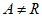 ,则
,则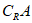 不具有性质P。
不具有性质P。
其中所有真命题的序号是________________。
三、解答题:共6小题,共85分。解答应写出文字说明,演算步骤或证明过程。
16.(本小题13分)
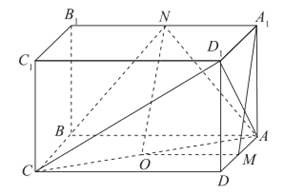
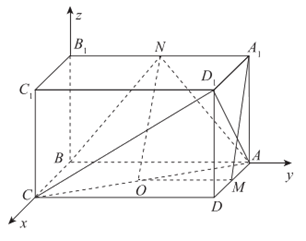
如图,在长方体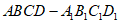 中,四边形
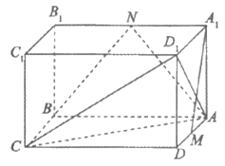
中,四边形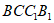 是边长为1的正方形,AB=2,M,N分别为
是边长为1的正方形,AB=2,M,N分别为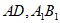 的中点。
的中点。
(Ⅰ)求证: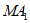 ∥平面
∥平面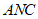 ;
;
(Ⅱ)求直线CN与平面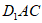 所成角的正弦值。
所成角的正弦值。
17. (本小题13分)
在△ABC中,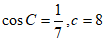 ,再从条件①、条件②这两个条件中选择一个作为已知,求:
,再从条件①、条件②这两个条件中选择一个作为已知,求:
(Ⅰ)b的值;
(Ⅱ)角A的大小和△ABC的面积。
条件①: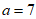 ;
;
条件②: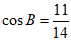 。
。
注:如果选择条件①、条件②分别解答,按第一个解答计分。
18.(本小题14分)
小明同学两次测试成绩(满分100分)如下表所示:
语文 | 数学 | 英语 | 物理 | 化学 | 生物 | |
第一次 | 87 | 92 | 91 | 92 | 85 | 93 |
第二次 | 82 | 94 | 95 | 88 | 94 | 87 |
(Ⅰ)从小明同学第一次测试的科目中随机抽取1科,求该科成绩大于90分的概率;
(Ⅱ)从小明同学第一次测试和第二次测试的科目中各随机抽取1科,记X为抽取的2科中成绩大于90分的科目数量,求X的分布列和数学期望E(X);
(Ⅲ)现有另一名同学两次测试成绩(满分100分)及相关统计信息如下表所示:
语文 | 数学 | 英语 | 物理 | 化学 | 生物 | 6科成绩均值 | 6科成绩方差 | |
第一次 |
|
|
|
|
|
|
| D1 |
第二次 |
|
|
|
|
|
|
| D2 |
将每科两次测试成绩的均值作为该科的总评成绩,这6科总评成绩的方差为D3。
有一种观点认为:若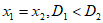 ,则
,则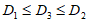 ,你认为这种观点是否正确?
,你认为这种观点是否正确?
(只写”正确”或”不正确”)
19. (本小题15分)
已知函数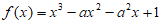 ,其中
,其中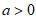 。
。
(Ⅰ)当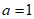 时,求
时,求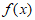 的单调区间;
的单调区间;
(Ⅱ)若曲线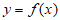 在点
在点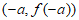 处的切线与y轴的交点为
处的切线与y轴的交点为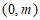 ,求
,求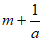 的最小值。
的最小值。
20.(本小题15分)
已知椭圆 过点
过点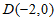 ,且焦距为
,且焦距为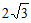 。
。
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点A(-4,0)的直线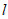 (不与x轴重合)与椭圆C交于P,Q两点,点T与点Q关于x轴对称,直线TP与x轴交于点H,是否存在常数
(不与x轴重合)与椭圆C交于P,Q两点,点T与点Q关于x轴对称,直线TP与x轴交于点H,是否存在常数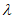 ,使得
,使得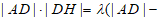
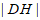 )成立,若存在,求出
)成立,若存在,求出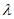 的值;若不存在,说明理由。
的值;若不存在,说明理由。
21.(本小题15分)
设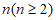 为正整数,若
为正整数,若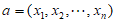 满足:
满足:
①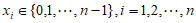 ;
;
②对于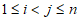 ,均有
,均有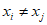 。
。
则称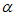 具有性质
具有性质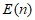 。
。
对于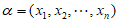 和
和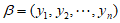 ,定义集合
,定义集合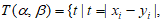
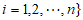 。
。
(I)设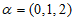 ,若
,若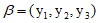 具有性质E(3),写出一个
具有性质E(3),写出一个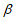 及相应的T(
及相应的T(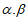 );
);
(II)设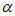 和
和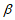 具有性质E(6),那么T(
具有性质E(6),那么T(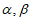 )是否可能为{0,1,2,3,4,5},若可能,写出一组
)是否可能为{0,1,2,3,4,5},若可能,写出一组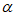 和
和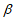 ,若不可能,说明理由;
,若不可能,说明理由;
(III)设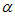 和
和 具有性质E(n),对于给定的
具有性质E(n),对于给定的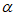 ,求证:满足
,求证:满足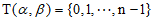 的
的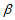 有偶数个。
有偶数个。
【试题答案】
一、选择题(共10小题,每小题4分,共40分)
1. C 2. B 3. A 4. B 5. D 6. C 7. B 8. C 9. A 10. D
二、填空题(共5小题,每小题5分,共25分)
11. 5 12. 4 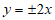 13.
13. 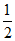 31 14. 4 15. ①②④
31 14. 4 15. ①②④
三、解答题(共6小题,共85分)
16. (本小题13分)
解:(Ⅰ)取AC中点O,连接OM,ON,
因为M是AD中点,
所以OM∥CD,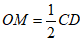 ,
,
在长方体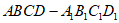 中,
中,
因为N是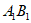 的中点,
的中点,
所以NA1∥CD,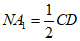 ,
,
所以NA1∥OM,且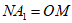 ,
,
所以四边形NOMA1是平行四边形,
所以MA1∥ON。
又因为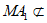 平面ANC,
平面ANC,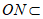 平面ANC,
平面ANC,
所以MA1∥平面ANC。 5分
(Ⅱ)在长方体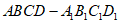 中,
中,
如图建立空间坐标系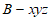 ,则
,则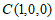 ,
,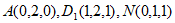 ,
,
所以 。
。
设平面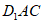 的法向量
的法向量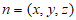 ,
,
由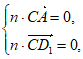 知
知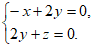
令 ,则
,则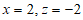 ,则平面
,则平面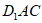 的法向量
的法向量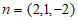 。
。
设直线CN与平面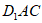 所成角为
所成角为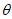 ,
,
则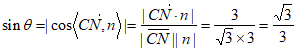 ,
,
所以直线CN与平面D1AC所成角的正弦值为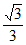 。 13分
。 13分
17.(本小题13分)
解:选择条件①。
(Ⅰ)因为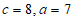 ,
,
由余弦定理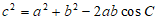 ,得
,得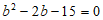 ,
,
解得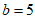 或
或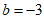 (舍),
(舍),
所以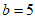 。 6分
。 6分
(Ⅱ)因为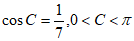 ,
,
所以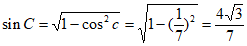 ,
,
由正弦定理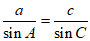 ,得
,得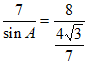 ,
,
所以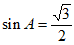 。
。
因为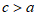 ,所以
,所以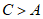 ,
,
所以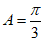 ,
,
所以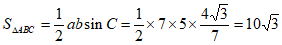 。 13分
。 13分
选择条件②。
(Ⅰ)因为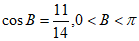 ,
,
所以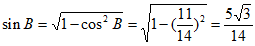 。
。
因为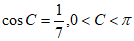 ,
,
所以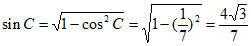 。
。
由正弦定理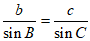 ,得
,得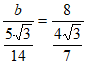 ,
,
解得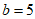 。 6分
。 6分
(Ⅱ)由(Ⅰ)知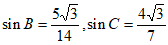 ,
,
又因为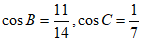 ,
,
在△ABC中,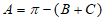 ,
,
所以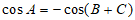
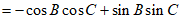
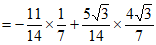
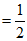 。
。
所以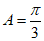 ,
,
所以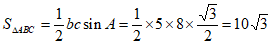 。 13分
。 13分
18. (本小题14分)
解:(Ⅰ)设事件A为“从小明同学第一次测试各科中随机选取1科,该科成绩大于90分“。
根据表中数据,在小明同学第一次测试的6科中,有4科的成绩大于90分,分别是数学,英语,物理,生物。
所以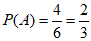 。 4分
。 4分
(Ⅱ)X的所有可能取值为0,1,2。
因为小明同学第一次测试的6科中,有4科的成绩大于90分,第二次测试的6科中,有3科的成绩大于90分,
所以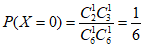 ,
,
 ,
,
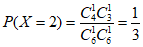 。
。
所以X的分布列为
X | 0 | 1 | 2 |
P |
|
|
|
故X的数学期望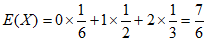 。 10分
。 10分
(Ⅲ)不正确。 14分
19.(本小题15分)
解:(Ⅰ)当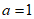 时,
时,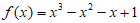 ,
,
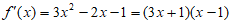 ,
,
当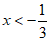 或
或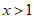 时,
时,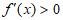 ;当
;当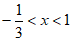 时,
时,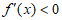 ,
,
所以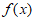 的单调递增区间为
的单调递增区间为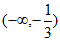 和
和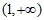 ,
,
单调递减区间为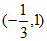 。 5分
。 5分
(Ⅱ)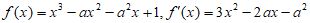 ,
,
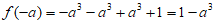 ,
,
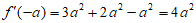 ,
,
曲线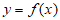 在点
在点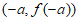 处的切线方程为
处的切线方程为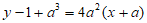 ,
,
即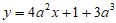 。
。
令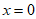 ,得
,得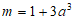 ,
,
此时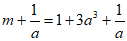 ,令
,令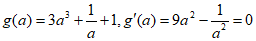 ,得
,得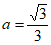 ,
,
当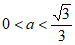 时,
时,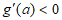 ;当
;当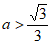 时,
时,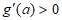 ,
,
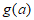 在区间
在区间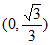 上单调递减,在区间
上单调递减,在区间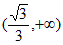 上单调递增,
上单调递增,
故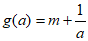 的最小值为
的最小值为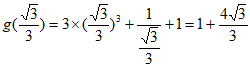 。 15分
。 15分
20.(本小题15分)
解:(Ⅰ)由题意得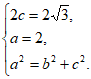 解得
解得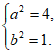
故椭圆C的方程为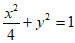 。 4分
。 4分
(Ⅱ)设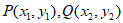 ,因为点T与点Q关于x轴对称,所以
,因为点T与点Q关于x轴对称,所以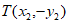 ,
,
所以直线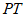 的斜率为
的斜率为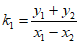 ,直线PT的方程:
,直线PT的方程: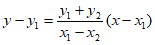 。
。
令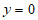 ,解得
,解得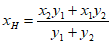 ,
,
所以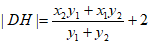 。
。
因为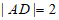 ,
,
“存在常数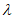 ,使得
,使得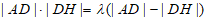 成立”
成立”
等价于”存在常数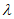 ,使得
,使得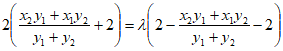 成立”,
成立”,
即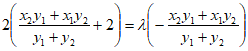 成立,
成立,
化简得: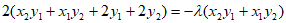 。
。
设直线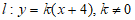 。
。
即”存在常数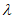 ,使得
,使得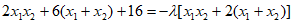 成立”。
成立”。
由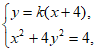 得
得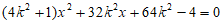 。
。
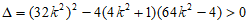 ,解得
,解得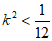 。
。
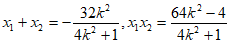 ,
,
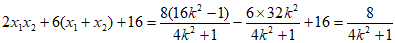 ,
,
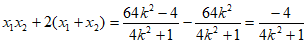 。
。
欲使
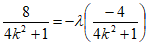 成立,只需
成立,只需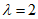 。
。
故存在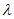 ,使得
,使得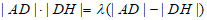 成立,
成立,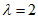 。 15分
。 15分
21.(本小题15分)
解:(Ⅰ)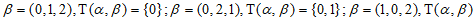 =
=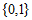 ;
;
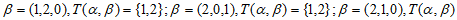 =
=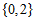 。 4分
。 4分
(Ⅱ)假设存在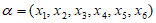 和
和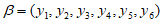 均具有性质
均具有性质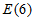 ,且
,且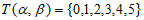 ,
,
则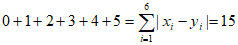 。
。
因为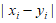 与
与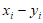 同奇同偶,
同奇同偶,
所以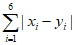 与
与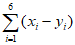 同奇同偶。
同奇同偶。
又因为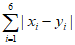 =15为奇数,
=15为奇数,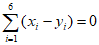 为偶数,
为偶数,
这与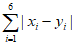 与
与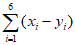 同奇同偶矛盾,
同奇同偶矛盾,
所以假设不成立。
综上,不存在均具有性质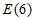 的
的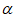 和
和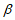 ,满足
,满足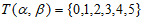 。 10分
。 10分
(Ⅲ)不妨设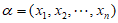 和
和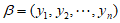 构成一个数表A:
构成一个数表A:
|
| … |
|
|
| … |
|
交换数表中两行,可得数表B:
|
| … |
|
|
| … |
|
调整数表各列的顺序,使第一行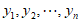 变为
变为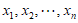 ,
,
设第二行变为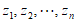 ,
,
令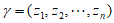 ,则
,则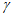 具有性质
具有性质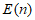 ,且
,且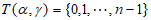 。
。
假设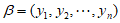 与
与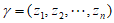 相同,
相同,
则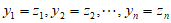 ,
,
不妨设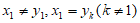 ,则有
,则有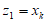 ,故
,故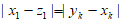 。
。
因为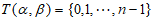 ,所以
,所以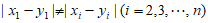 ,
,
因为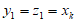 ,所以
,所以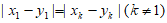 ,
,
与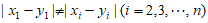 矛盾。
矛盾。
故对于具有性质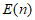 的
的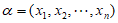 ,若
,若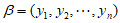 具有性质
具有性质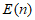 ,
,
且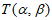 =
=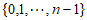 ,
,
则存在一个具有性质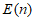 的
的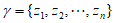 ,
,
使得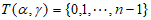 ,且
,且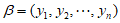 与
与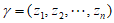 不同,
不同,
并且由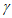 的构造过程可以知道,当
的构造过程可以知道,当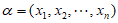 ,
,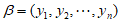 确定时,
确定时,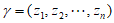 唯一确定。由
唯一确定。由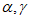 也仅能构造出
也仅能构造出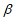 。
。
综上,命题得证。 15分