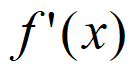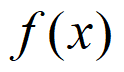(考试时间120分钟
满分150分)
本试卷分为选择题(共40分)和非选择题(共110分)两部分
第一部分(选择题
共40分)
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 已知集合A={-1,0,1,2,3},B={x|x-1≥0},则A∩B=
A. {0,1,2,3} B. {1,2,3} C. {2,3} D. {3}
2. 如果复数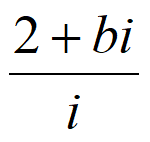 (b∈R)的实部与虚部相等,那么b=
(b∈R)的实部与虚部相等,那么b=
A. -2 B. 1 C. 2 D. 4
3. 已知等差数列{an}的前n项和为Sn,a3=1,S9=18,则a1=
A. 0 B. -1 C. -2 D. -3
4. 已知圆x2+y2=4截直线y=kx+2所得弦的长度为2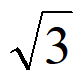 ,则实数k=
,则实数k=
A. 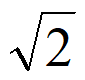 B. –
B. –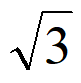 C. ±
C. ±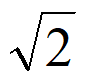 D. ±
D. ±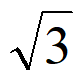
5. 已知双曲线C: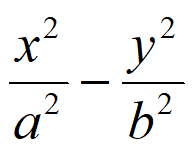 =1(a>0,b>0)的离心率为2,则双曲线C的渐近线方程为
=1(a>0,b>0)的离心率为2,则双曲线C的渐近线方程为
A. y=±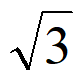 x B. y=±
x B. y=±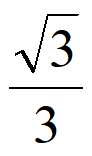 x C. y= ±
x C. y= ±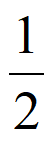 x D. y=±2x
x D. y=±2x
6. 在△ABC中,若a2-b2+c2+ac=0,则B=
A. 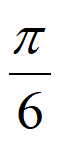 B.
B. 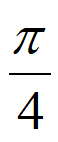 C.
C. 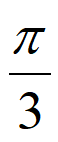 D.
D. 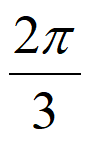
7. 某三棱锥的三视图如图所示,已知网格纸上小正方形的边长为1,则该三棱锥最长的棱长为
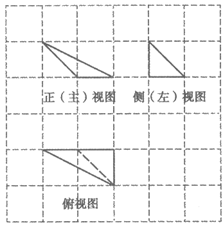
A. 2 B. 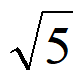 C.
C. 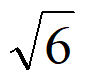 D. 2
D. 2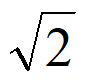
8. 在△ABC中,”tanAtanB<1″是“△ABC为钝角三角形“的
A. 充分而不必要条件
B. 必要而不充分条件
C. 充分必要条件
D. 既不充分也不必要条件
9. 已知抛物线C:y2=4x的焦点为F,准线为l,点P是直线l上的动点。若点A在抛物线C上,且|AF|=5,则|PA|+|PO|(O为坐标原点)的最小值为
A. 8 B. 2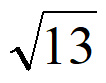 C.
C. 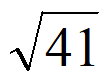 D. 6
D. 6
10. 在棱长为1的正方体ABCD-A1B1C1D1中,P是线段BC1上的点,过A1的平面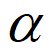 与直线PD垂直。当P在线段BC1上运动时,平面
与直线PD垂直。当P在线段BC1上运动时,平面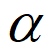 截正方体ABCD-A1B1C1D1所得的截面面积的最小值是
截正方体ABCD-A1B1C1D1所得的截面面积的最小值是
A. 1 B. 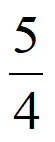 C.
C. 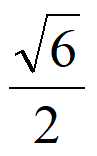 D.
D. 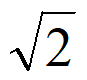
第二部分(非选择题
共110分)
二、填空题共5小题,每小题5分,共25分。
11. 在(x+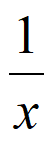 )8的展开式中,x4的系数为_________。(用数字作答)
)8的展开式中,x4的系数为_________。(用数字作答)
12. 已知函数f(x)=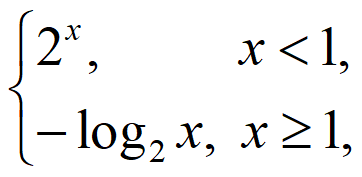 则f(0)=_________;f(x)的值域为_________。
则f(0)=_________;f(x)的值域为_________。
13. 已知向量a=(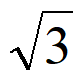 ,1),b=(x,y)(xy≠0),且|b|=1,a·b<0,则向量b的坐标可以是________。(写出一个即可)
,1),b=(x,y)(xy≠0),且|b|=1,a·b<0,则向量b的坐标可以是________。(写出一个即可)
14. 李明自主创业,经营一家网店,每售出一件A商品获利8元。现计划在“五一“期间对A商品进行广告促销,假设售出A商品的件数m(单位:万件)与广告费用x(单位:万元)符合函数模型m=3-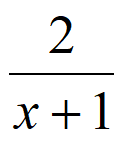 。若要使这次促销活动获利最多,则广告费用x应投入_________万元。
。若要使这次促销活动获利最多,则广告费用x应投入_________万元。
15. 华人数学家李天岩和美国数学家约克给出了“混沌“的数学定义,由此发展的混沌理论在生物学、经济学和社会学领域都有重要作用。在混沌理论中,函数的周期点是一个关键概念,定义如下:设f(x)是定义在R上的函数,对于x0∈R,令xn=f(xn-1)(n=1,2,3,…),若存在正整数k使得xk=x0,且当0<j<k时,xj≠x0,则称x0是f(x)的一个周期为k的周期点。给出下列四个结论:
①若f(x)=ex-1,则f(x)存在唯一一个周期为1的周期点;
②若f(x)=2(1-x),则f(x)存在周期为2的周期点;
③若f(x)=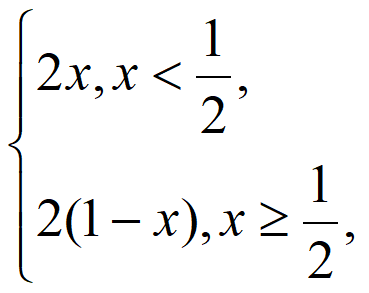 则f(x)不存在周期为3的周期点;
则f(x)不存在周期为3的周期点;
④若f(x)=x(1-x),则对任意正整数n,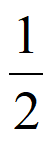 都不是f(x)的周期为n的周期点。
都不是f(x)的周期为n的周期点。
其中所有正确结论的序号是_________。
三、解答题共6小题,共85分。解答应写出文字说明,演算步骤或证明过程。
16.(本小题13分)
已知函数f(x)=Asin(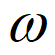 x+
x+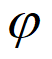 )(A>0,
)(A>0,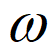 >0,0<
>0,0<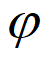 <
<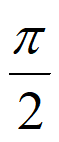 )由下列四个条件中的三个来确定:
)由下列四个条件中的三个来确定:
①最小正周期为 ;②最大值为2;③f(–
;②最大值为2;③f(–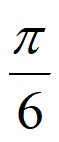 )=0;④f(0)=-2。
)=0;④f(0)=-2。
(I)写出能确定f(x)的三个条件,并求f(x)的解析式;
(Ⅱ)求f(x)的单调递增区间。
17.(本小题13分)
如图,在四棱锥P-ABCD中,O是AD边的中点,PO⊥底面ABCD,PO=1。在底面ABCD中,BC∥AD,CD⊥AD,BC=CD=1,AD=2。
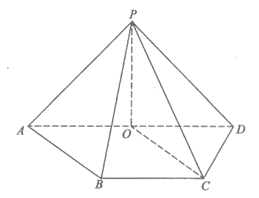
(I)求证:AB∥平面POC;
(Ⅱ)求二面角B-AP-D的余弦值。
18.(本小题14分)
我国脱贫攻坚战取得全面胜利,现行标准下农村贫困人口全部脱贫,消除了绝对贫困。为了解脱贫家庭人均年纯收入情况,某扶贫工作组对A,B两个地区2019年脱贫家庭进行简单随机抽样,共抽取500户家庭作为样本,获得数据如下表:
A地区 | B地区 | |
2019年人均年纯收入超过10000元 | 100户 | 150户 |
2019年人均年纯收入未超过10000元 | 200户 | 50户 |
假设所有脱贫家庭的人均年纯收入是否超过10000元相互独立。
(I)从A地区2019年脱贫家庭中随机抽取1户,估计该家庭2019年人均年纯收入超过10000元的概率;
(Ⅱ)在样本中,分别从A地区和B地区2019年脱贫家庭中各随机抽取1户,记X为这2户家庭中2019年人均年纯收入超过10000元的户数,求X的分布列和数学期望;
(Ⅲ)从样本中A地区的300户脱贫家庭中随机抽取4户,发现这4户家庭2020年人均年纯收入都超过10000元。根据这个结果,能否认为样本中A地区2020年人均年纯收入超过10000元的户数相比2019年有变化?请说明理由。
19.(本小题15分)
已知椭圆C的短轴的两个端点分别为A(0,1),B(0,-1),离心率为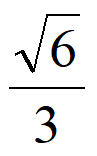 。
。
(I)求椭圆C的方程及焦点的坐标;
(Ⅱ)若点M为椭圆C上异于A,B的任意一点,过原点且与直线MA平行的直线与直线y=3交于点P,直线MB与直线y=3交于点Q,试判断以线段PQ为直径的圆是否过定点?若过定点,求出定点的坐标;若不过定点,请说明理由。
20.(本小题15分)
已知函数f(x)=(ax-1)ex(a∈R)。
(I)求f(x)的单调区间;
(Ⅱ)若直线y=ax+a与曲线y=f(x)相切,求证:a∈(-1,–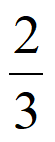 )。
)。
21. (本小题15分)
设数列Am:a1,a2,…,am(m≥2),若存在公比为q的等比数列Bm+1:b1,b2,…,bm+1,使得bk<ak<bk+1,其中k=1,2,…,m,则称数列Bm+1为数列Am的“等比分割数列“。
(I)写出数列A4:3,6,12,24的一个“等比分割数列“B5;
(Ⅱ)若数列A10的通项公式为an=2n(n=1,2,…,10),其“等比分割数列“B11的首项为1,求数列B11的公比q的取值范围;
(Ⅲ)若数列Am的通项公式为an=n2(n=1,2,…,m),且数列Am存在“等比分割数列“,求m的最大值。
参考答案
一、选择题(共10小题,每小题4分,共40分)
1. B 2. A 3. A 4. D 5. A
6. D 7. C 8. C 9. B 10. C
二、填空题(共5小题,每小题5分,共25分)
11. 28
12. 1;(-∞,2)
13. (–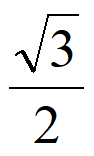 ,
,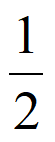 )(答案不唯一)
)(答案不唯一)
14. 3
15. ①④
三、解答题(共6小题,共85分)
16.(共13分)
解:(I)确定f(x)的三个条件是①,②,③。
当A>0且0<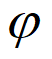 <
<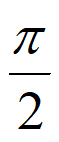 时,Asin
时,Asin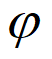 >0。
>0。
若函数f(x)满足条件④,则f(0)=Asin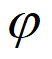 =-2,
=-2,
与Asin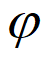 >0矛盾,所以f(x)不能满足条件④。
>0矛盾,所以f(x)不能满足条件④。
所以能确定f(x)的三个条件是①,②,③。
由条件①,得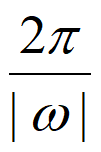 =
=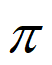 ,又
,又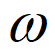 >0,所以
>0,所以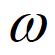 =2。
=2。
由条件②,得|A|=2,又A>0,所以A=2。
由条件③,得f(–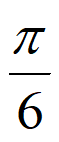 )=2sin(–
)=2sin(–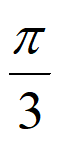 +
+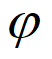 )=0,又0<
)=0,又0<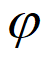 <
<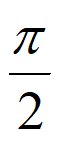 ,所以
,所以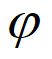 =
=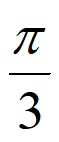 。
。
所以f(x)=2sin(2x+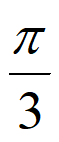 )。
)。
经验证,f(x)=2sin(2x+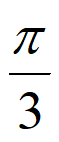 )符合题意。 ……7分
)符合题意。 ……7分
(Ⅱ)函数y=sinx的单调递增区间为[2k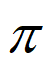 –
–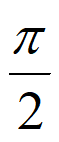 ,2k
,2k +
+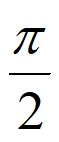 ](k∈Z)。
](k∈Z)。
由2k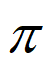 –
–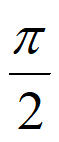 ≤2x+
≤2x+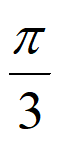 ≤2k
≤2k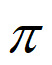 +
+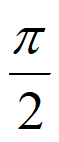 (k∈Z),
(k∈Z),
得k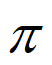 –
–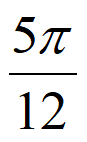 ≤x≤k
≤x≤k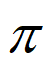 +
+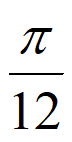 (k∈Z)。
(k∈Z)。
所以f(x)的单调递增区间为[k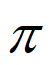 –
–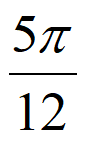 ,k
,k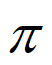 +
+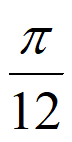 ](k∈Z).…13分
](k∈Z).…13分
17.(共13分)
解:(I)在四边形ABCD中,
因为BC∥AD,BC= AD,O是AD的中点,则BC∥AO,BC=AO。
AD,O是AD的中点,则BC∥AO,BC=AO。
所以四边形ABCO是平行四边形。
所以AB∥OC。
又因为AB¢平面POC,OC 平面POC,
平面POC,
所以AB∥平面POC。 5分
(Ⅱ)连结OB。因为PO⊥平面ABCD,
所以PO⊥OB,PO⊥OD。
又因为点O是AD的中点,且BC=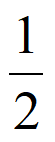 AD,
AD,
所以BC=OD。
因为BC∥AD,CD⊥AD,BC=CD,
所以四边形OBCD是正方形。所以BO⊥AD。
如图,建立空间直角坐标系O-xyz,
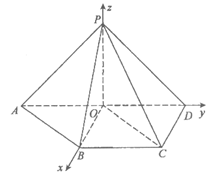
则A(0,-1,0),B(1,0,0),C(1,1,0),D(0,1,0),P(0,0,1)。
所以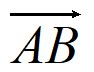 =(1,1,0),
=(1,1,0),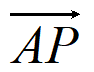 =(0,1,1)。
=(0,1,1)。
设m=(x,y,z)是平面BAP的一个法向量,
则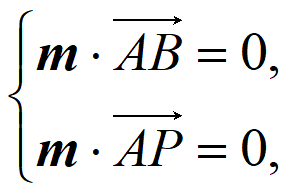 即
即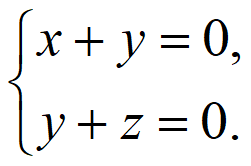
令y=1,则m=(-1,1,-1)。
因为OB⊥平面PAD,
所以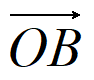 =(1,0,0)是平面PAD的一个法向量。
=(1,0,0)是平面PAD的一个法向量。
所以|cos<m,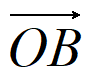 >|=|
>|=|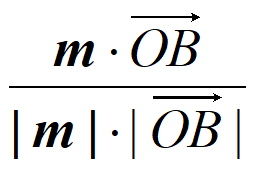 |=|
|=|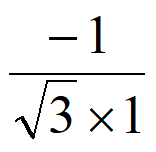 |=
|=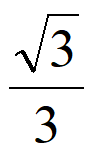 。
。
由图可知,二面角B-AP-D为锐角,
所以二面角B-AP-D的余弦值为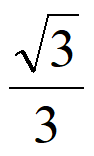 。 13分
。 13分
18.(共14分)
解:(I)设事件C:从A地区2019年脱贫家庭中随机抽取1户,该家庭2019年人均年纯收入超过10000元。
从表格数据可知,A地区抽出的300户家庭中2019年人均年收入超过10000元的有100户,因此P(C)可以估计为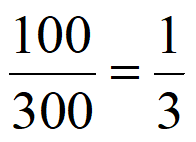 。 3分
。 3分
(Ⅱ)设事件A:从样本中A地区2019年脱贫家庭中随机抽取1户,该家庭2019年人均年纯收入超过10000元,则P(A)=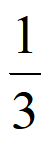 。
。
设事件B:从样本中B地区2019年脱贫家庭中随机抽取1户,该家庭2019年人均年纯收入超过10000元,则P(B)=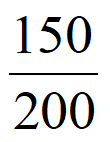 =
=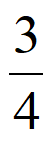 。
。
由题可知X的可能取值为0,1,2。
P(X=0)=P(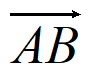 )=P(
)=P(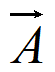 )P(
)P(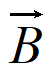 )=(1-
)=(1-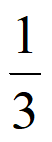 )(1-
)(1-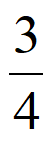 )=
)=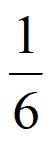 ;
;
P(X=1)=P(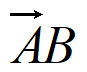
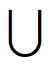
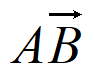 )=P(
)=P(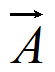 )P(B)+P(A)P(
)P(B)+P(A)P(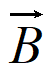 )=(1-
)=(1-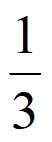 )×
)×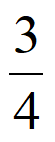 +
+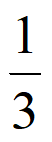 ×(1-
×(1-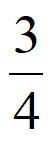 )=
)=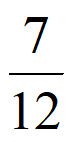 ;
;
P(X=2)=P(AB)=P(A)P(B)=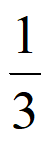 ×
×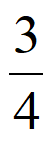 =
=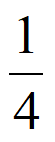 。
。
所以X的分布列为
X | 0 | 1 | 2 |
P |
|
|
|
所以X的数学期望EX=0×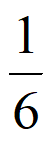 +1×
+1×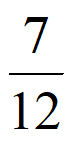 +2×
+2×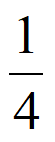 =
=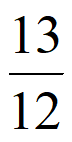 。………10分
。………10分
(Ⅲ)记事件E为“从样本中A地区的300户脱贫家庭中随机抽取4户,这4户家庭2020年人均年纯收入都超过10000元“。
假设样本中A地区2020年人均年纯收入超过10000元的户数相比2019年没有变化,
则由2019年的样本数据得P(E)=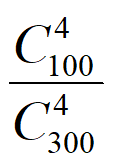 ≈0.012。
≈0.012。
答案示例1:可以认为有变化。理由如下:
P(E)比较小,概率比较小的事件一般不容易发生。一旦发生,就有理由认为样本中A地区2020年人均年纯收入超10000元的户数相比2019年发生了变化。
所以可以认为有变化。
答案示例2:无法确定有没有变化。理由如下:
事件E是随机事件,P(E)比较小,一般不容易发生,但还是有可能发生的,
所以无法确定有没有变化。 .………14分
19.(共15分)
解:(I)由题意可设椭圆C的方程为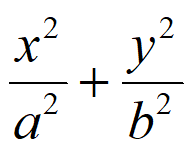 =1(a>b>0),则
=1(a>b>0),则
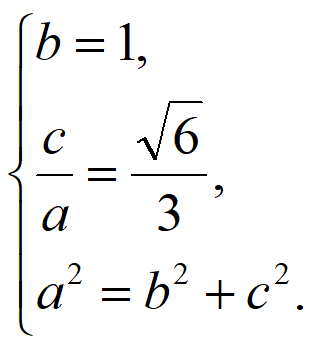
解得a=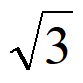 ,c=
,c=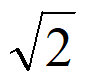 。
。
所以椭圆C的方程为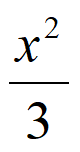 +y2=1,焦点坐标为(–
+y2=1,焦点坐标为(–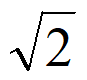 ,0)和(
,0)和(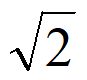 ,0)。……5分
,0)。……5分
(Ⅱ)方法1:
设点M的坐标为(x0,y0)(x0≠0,y0≠±1),则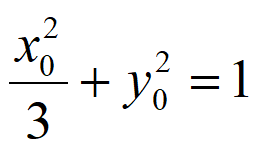 。
。
过原点且与直线MA平行的直线方程为y=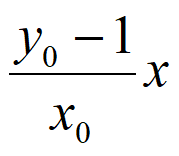 。
。
令y=3,得P(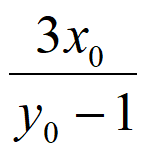 ,3)
,3)
直线MB的方程为y=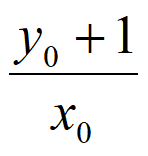 x-1,
x-1,
令y=3,得Q(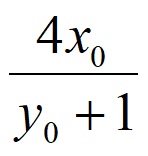 ,3)。
,3)。
假设以线段PQ为直径的圆过定点,由椭圆的对称性可设定点为N(0,m)。
则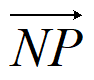 ·
·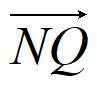 =0。
=0。
因为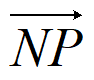 =(
=(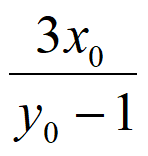 ,3-m),
,3-m),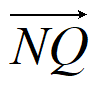 =(
=(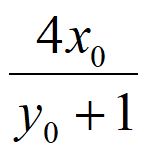 ,3-m),
,3-m),
所以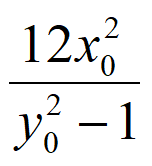 +(3-m)2=0。
+(3-m)2=0。
因为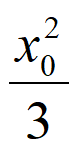 +
+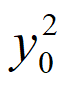 =1,所以m2-6m-27=0。
=1,所以m2-6m-27=0。
则m=-3或m=9。
所以以线段PQ为直径的圆过定点,且定点坐标为(0,-3)和(0,9)。…15分
方法2:
设点M的坐标为(x0,y0)(x0≠0,y0≠±1),则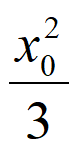 +
+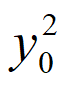 =1。
=1。
过原点且与直线MA平行的直线方程为y=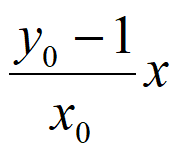 。
。
令y=3,得xp=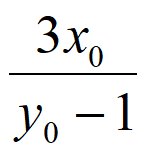 。
。
直线MB的方程为y=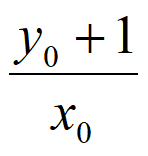 x-1,
x-1,
令y=3,得xQ=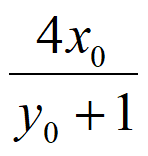 。
。
所以以PQ为直径的圆的半径为
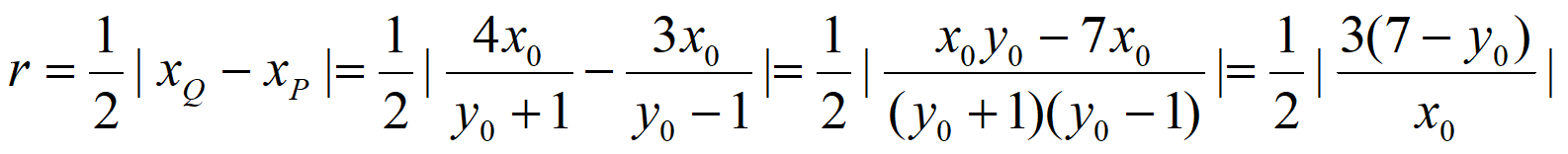 。
。
圆心的横坐标为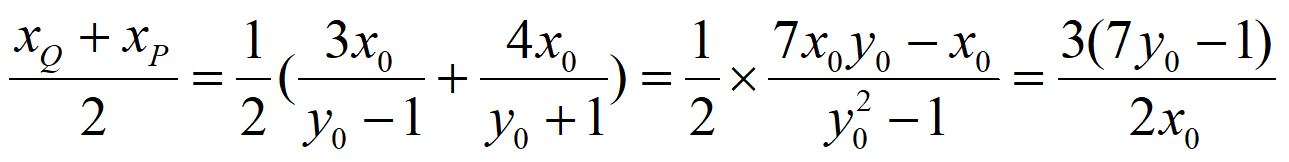 。
。
所以以线段PQ为直径的圆的方程为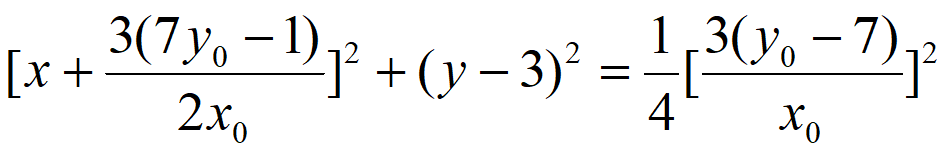 。
。
因为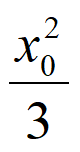 +
+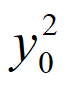 =1,所以
=1,所以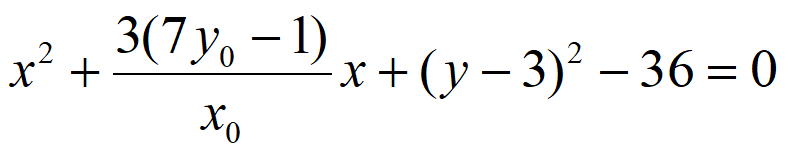 。
。
以线段PQ为直径的圆过定点等价于对任意的点M(x0,y0),
方程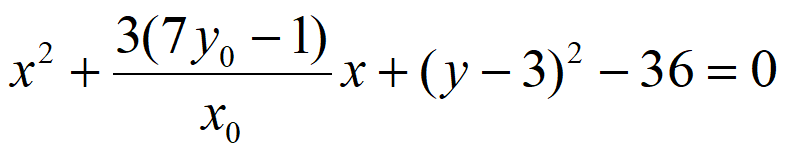 恒成立。
恒成立。
所以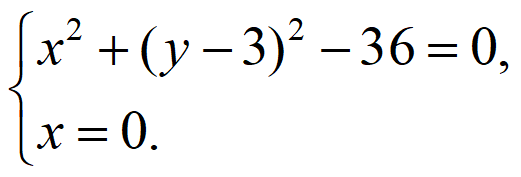
解得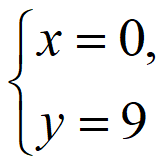 或
或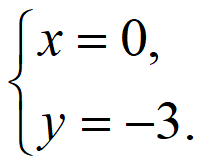
所以以线段PQ为直径的圆过定点,且定点坐标为(0,-3)和(0,9)。…15分
20.(共15分)
解:(I)f'(x)=(ax+a-1)ex。令f'(x)=0,得ax=1-a。
当a=0时,f'(x)=-ex<0,y=f(x)在(-∞,+∞)上单调递减;
当a>0时,f'(x)和f(x)在R上的变化情况如下:
| (- |
| ( |
| – | 0 | + |
| ↘ | 极小值 | ↗ |
当a<0时,f'(x)和f(x)在R上的变化情况如下:
| (- |
| ( |
| + | 0 | – |
| ↗ | 极大值 | ↘ |
综上,当a=0时,y=f(x)在(-∞,+∞)上单调递减,
当a>0时,y=f(x)的单调递减区间为(-∞,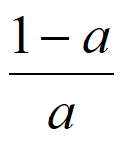 ),单调递增区间为(
),单调递增区间为(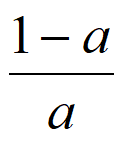 ,+∞),
,+∞),
当a<0时,y=f(x)的单调递增区间为(-∞,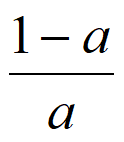 ),单调递减区间为(
),单调递减区间为(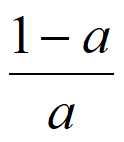 ,+∞)。
,+∞)。
……6分
(Ⅱ)由题得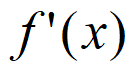 =(ax+a-1)ex。
=(ax+a-1)ex。
设直线y=ax+a与曲线y=f(x)相切于点(x0,y0),
则
由①–②得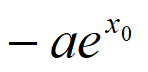 =ax0,即a(
=ax0,即a(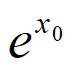 +x0)=0。
+x0)=0。
若a=0,则f(x)=-ex,ax+a=0,
直线y=0与曲线y=f(x)不相切,不符合题意,所以a≠0。
所以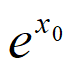 +x0=0。③
+x0=0。③
令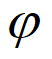 (x)=ex+x,则φ’(x)=ex+1>0,所以
(x)=ex+x,则φ’(x)=ex+1>0,所以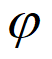 (x)单调递增。
(x)单调递增。
因为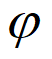 (–
(–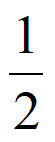 )=
)=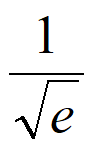 –
–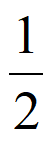 >0,
>0,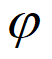 (-1)=e-1-1<0,
(-1)=e-1-1<0,
所以存在唯一x0∈(-1,–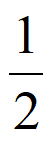 )使得
)使得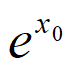 +x0=0。
+x0=0。
将③代入①得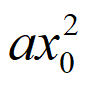 +ax0-x0+a=0。
+ax0-x0+a=0。
所以a=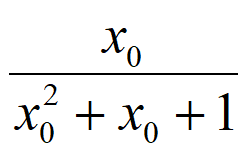 =
=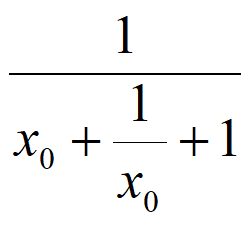 。
。
易知在(-1,–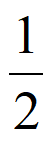 )内y=x+
)内y=x+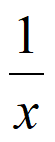 +1单调递减,且x+
+1单调递减,且x+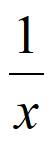 +1<0,
+1<0,
所以y=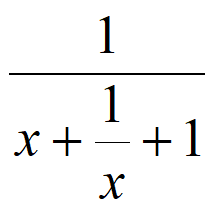 在(-1,–
在(-1,–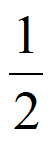 )内单调递增。
)内单调递增。
因为x0∈(-1,–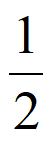 ),所以-1<a<–
),所以-1<a<–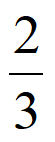 ,所以a∈(-1,–
,所以a∈(-1,–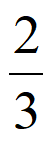 )。.…15分
)。.…15分
21.(共15分)
解:(I)B5;2,4,8,16,32。(答案不唯一)……3分
(Ⅱ)由bk<ak<bk+1,得qk-1<2k<q k,k=1,2,…,10,
所以2<q<2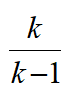 ,k=2,3,…,10。
,k=2,3,…,10。
令f(k)=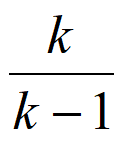 =1+
=1+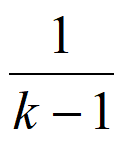 ,k=2,3,…,10,
,k=2,3,…,10,
则f(k)单调递减。
所以2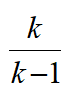 (k=2,3,…,10)的最小值为2
(k=2,3,…,10)的最小值为2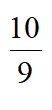 。
。
所以2<q<2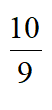 ,即公比q的取值范围是(2,2
,即公比q的取值范围是(2,2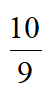 )。 .…8分
)。 .…8分
(Ⅲ)首先证明当m≥6时,数列Am不存在“等比分割数列”
假设当m≥6时,数列Am存在“等比分割数列“Bm+1,
则b1<1<b2=b1q<4<b1q2<9<b1q3<16<b1q4<25<…<m2<b1 q m。
易知b1>0,q>0。
因为0<b1<1,且4<b1q2,所以q2>4。因为q>0,所以q>2。
又因为9<b1q3,所以b6=b1q5=b1q3·q2>36=62,
与b6<a6=36矛盾。
所以当m≥6时,数列Am不存在“等比分割数列“。
所以m≤5。
当m=5时,数列A5:1,4,9,16,25,存在首项为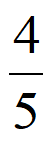 公比为
公比为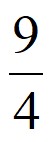 的数列B6满足:
的数列B6满足:
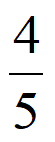 <1<
<1<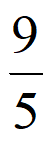 <4<
<4<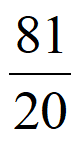 <9<
<9<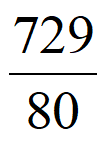 <16<
<16<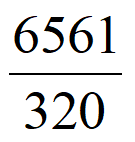 <25<
<25<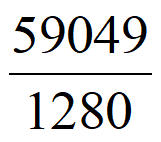 。
。
所以m=5时,数列Am存在“等比分割数列“。
所以m的最大值为5。 .……15分

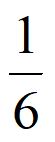
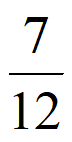
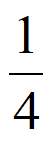
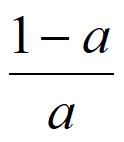
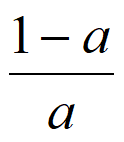
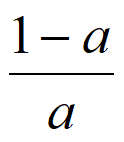 ,
,
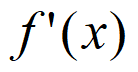
 ,
,