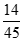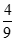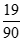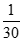本试卷满分共150分 考试时间120分钟
第一部分(选择题 共40分)
一、选择题共 10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.
1.若集合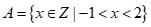 ,
,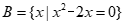 ,则A∪B=
,则A∪B=
(A) {0} (B){0,1} (C){0,1,2} (D){-1,0,1,2}
2.已知向量a=(x,2),b=(-2,1),满足a //b ,则x=
(A) 1 (B)-1 (C)4 (D)-4
3.若复数z满足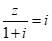 ,则z对应的点位于
,则z对应的点位于
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
4.圆(x-1)2 +y2 =2的圆心到直线x +y+ 1 =0的距离为
(A) 2 (B)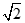
(C)1 (D)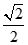
5.已知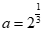 ,
,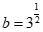 ,
,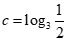 ,则
,则
(A)a> b>c (B)a>c> b
(C)b> a>c (D)b> c> a
6.”a>1″是”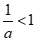 “成立的
“成立的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
7.某三棱锥的三视图如图所示,则该三棱锥的四个面中,面积等于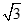 的有
的有
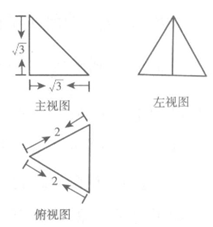
(A)1个 (B)2个 (C)3个 (D)4个
8.过抛物线C:y2=2px(p>0)的焦点F作倾斜角为60°的直线与抛物线C交于两个不同的点A,B(点A在x轴上方),则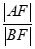 的值为
的值为
(A)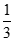 (B)
(B)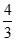 (C)
(C)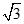 (D) 3
(D) 3
9.将函数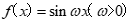 的图象向左平移
的图象向左平移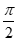 个单位长度后得到函数g(x)的图象,且g(0)= 1,下列说法错误的是
个单位长度后得到函数g(x)的图象,且g(0)= 1,下列说法错误的是
(A)g(x)为偶函数
(B)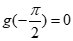
(C)当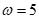 时,g(x)在
时,g(x)在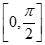 上有3个零点
上有3个零点
(D)若g(x)在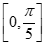 上单调递减,则
上单调递减,则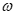 的最大值为9
的最大值为9
10.已知函数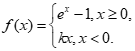 若存在非零实数
若存在非零实数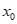 ,使得
,使得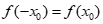 成立,则实数k的取值范围是
成立,则实数k的取值范围是
(A)(-∞,-1) (B)(-∞,-1]
(C)(-1,0) (D)[-1,0)
第二部分(非选择题 共 110分)
二、填空题共5小题,每小题5分,共25分.
11.设数列{an}的前n项和为Sn,an=2n-1,则S5=________________.
12.若x>1,则函数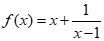 的最小值为________________,此时x=________________.
的最小值为________________,此时x=________________.
13.已知平面α和三条不同的直线m,n,l.给出下列六个论断:①m⊥α;②m//α;
③m//l;④n⊥α;⑤n//α;⑥n //l.以其中两个论断作为条件,使得m//n成立.这两个论断可以是____________.(填上你认为正确的一组序号)
14.如果对某对象连续实施两次变换后的结果就是变换前的对象,那么我们称这种变换为”回归”变换.如:对任意一个实数,变换:取其相反数.因为相反数的相反数是它本身,所以变换”取实数的相反数”是一种”回归”变换.有下列3种变换:
①对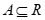 ,变换:求集合A的补集;
,变换:求集合A的补集;
②对任意z∈C,变换:求z的共轭复数;
③对任意x∈R ,变换: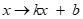 (k,b均为非零实数).
(k,b均为非零实数).
其中是”回归”变换的是___________.
注:本题给出的结论中,有多个符合题目要求.全部选对得5分,不选或有错选得0分,其他得3分.
15.已知双曲线M: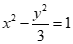 的渐近线是边长为1的菱形OABC的边OA,OC所在直线.若椭圆N:
的渐近线是边长为1的菱形OABC的边OA,OC所在直线.若椭圆N: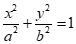 (a>b>0)经过A,C两点,且点B是椭圆N的一个焦点,则a=_________.
(a>b>0)经过A,C两点,且点B是椭圆N的一个焦点,则a=_________.
三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.
16. (本小题共14分)
在△ABC中,角A,B,C所对的边分别为a,b,c.已知c=4,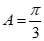
(I)当b=2时,求a ;
(II)求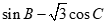 的取值范围.
的取值范围.
17.(本小题共14分)
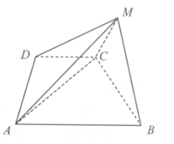
如图,在四棱锥M-ABCD中,AB//CD,∠ADC=∠BMC=90°,MB=MC,AD=DC=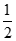 AB=
AB=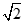 ,平面BCM⊥平面ABCD.
,平面BCM⊥平面ABCD.
(I)求证:CD//平面ABM;
(II)求证:AC⊥平面BCM;
(III)在棱AM上是否存在一点E,使得二面角E-BC-M的大小为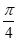 ?若存在,求出
?若存在,求出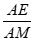 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
18.(本小题共14分)
在抗击新冠肺炎疫情期间,很多人积极参与了疫情防控的志愿者活动.各社区志愿者服务类型有:现场值班值守,社区消毒,远程教育宣传,心理咨询(每个志愿者仅参与一类服务).参与A,B,C三个社区的志愿者服务情况如下表:
社区 | 社区服务总人数 | 服务类型 | |||
现场值班值守 | 社区消毒 | 远程教育宣传 | 心理咨询 | ||
A | 100 | 30 | 30 | 20 | 20 |
B | 120 | 40 | 35 | 20 | 25 |
C | 150 | 50 | 40 | 30 | 30 |
(I)从上表三个社区的志愿者中任取1人,求此人来自于A社区,并且参与社区消毒工作的概率;
(II)从上表三个社区的志愿者中各任取1人调查情况,以x表示负责现场值班值守的人数,求X的分布列;
(III)已知A社区心理咨询满意率为0.85,B社区心理咨询满意率为0.95,C社区心理咨询满意率为0.9,”ξA=1,ξB=1,ξC=1″分别表示A,B,C社区的人们对心理咨询满意,”ξA=0,ξB=0,ξC=0″分别表示A,B,C社区的人们对心理咨询不满意,写出方差D(ξA),D(ξB),D(ξC)的大小关系. (只需写出结论)
19.(本小题共15分)
已知函数f(x)=(x+a)lnx-x+1.
(I)若曲线y=f(x)在点(e,f(e))处的切线斜率为1,求实数a的值;
(II)当a=0时,求证:f(x)≥0;
(IIIA)若函数f(x)在区间(1,+∞)上存在极值点,求实数a的取值范围.
20.(本小题共14分)
已知椭圆C: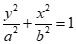 (a>b>0)的离心率为
(a>b>0)的离心率为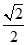 ,点P(1,0) 在椭圆C上,直线
,点P(1,0) 在椭圆C上,直线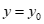 与椭圆C交于不同的两点A,B.
与椭圆C交于不同的两点A,B.
(I)求椭圆C的方程;
(II)直线PA,PB分别交y轴于M,N两点,问:x轴上是否存在点Q,使得∠OQN+∠OQM=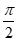 ?若存在,求出点Q的坐标;若不存在,请说明理由.
?若存在,求出点Q的坐标;若不存在,请说明理由.
21.(本小题共14分)
已知有穷数列A:a1,a2,…,ak,…an(n∈N*且n≥3).定义数列A的”伴生数列”B:b1,b2,…,bk,…bn,其中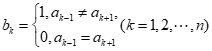 ,规定
,规定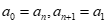 .
.
(I)写出下列数列的”伴生数列”:
①1,2,3,4,5;
②1,-1,1,-1,1.
(II)已知数列B的”伴生数列”C:c1,c2,…,ck,…cn,且满足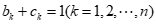 .
.
(i)若数列B中存在相邻两项为1,求证:数列B中的每一项均为1.
(ii)求数列C所有项的和.
参考答案
一、选择题共10小题,每小题4分,共40分.
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | C | D | B | B | C | A | C | D | D | A |
二、填空题共5小题,每小题5分,共25分
11.25 12.3;2 13.①④(或③⑥)
14.①② 15.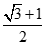
三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.
16.(本小题共14分)
解:(I)由余弦定理a2=b2+c2-2bccosA,
得a2=22 +42-2×2×4·cos
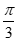 =12.
=12.
所以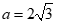 .…………………………6分
.…………………………6分
(II)由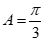 可知,
可知,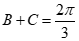 ,即
,即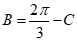 .
.
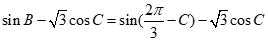
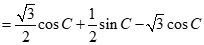
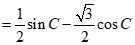
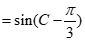 .
.
因为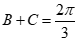 ,所以C∈(
,所以C∈(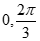 )故
)故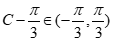 .
.
因此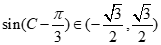
于是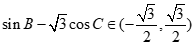 ……………………4.分
……………………4.分
17.(本小题共14分)
证明:(I)因为AB//CD,
AB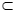 平面ABM,
平面ABM,
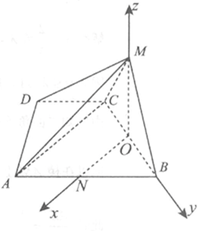
CD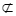 平面ABM ,
平面ABM ,
所以CD //平面ABM.…………………………3分
(II)取AB的中点N,连接CN.
在直角梯形ABCD中,
易知AN= BN=CD=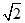 ,且CN⊥AB.
,且CN⊥AB.
在Rt△CNB中,由勾股定理得BC=2.
在△ACB中,由勾股定理逆定理可知AC⊥BC.
又因为平面BCM⊥平面ABCD,
且平面BCM∩平面ABCD = BC,
所以AC⊥平面BCM. …………………………7分
(III)取BC的中点O,连接OM,ON.
所以ON// AC,
因为AC⊥平面BCM,
所以ON⊥平面BCM.
因为BM=MC,
所以OM⊥BC.
如图建立空间直角坐标系O-xyz ,
则M(0,0,1),B(0,1,0),C(0,-1,0),A(2,-1,0),
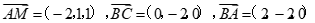 .
.
易知平面BCM的一个法向量为m=(1,0,0).
假设在棱AM上存在一点E,使得二面角E-BC-M的大小为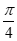
不妨设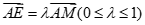 ,
,
所以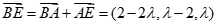 ,
,
设n=(x,y,z)为平面BCE的一个法向量,
则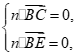 即
即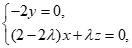
令x=λ,z=2λ-2,所以n=(λ,0,2λ-2)
从而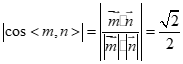 .
.
解得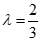 或λ=2.
或λ=2.
因为0≤λ≤1,所以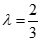
由题知二面角E-BC-M为锐二面角.
所以在棱AM上存在一点E,使得二面角E-BC-M的大小为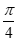 ,
,
此时 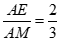 .……………………………………14分
.……………………………………14分
18.(本小题共14分)
解:(I)记”从上表三个社区的志愿者中任取1人,此人来自于A社区,并且参与社区消毒工作”为事件D
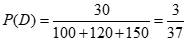 .
.
所以从上表三个社区的志愿者中任取1人,此人来自于A社区,并且参与社区消毒工作的概率为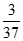 …………………………4分
…………………………4分
(II)从上表三个社区的志愿者中各任取1人,由表可知: A,B,C三个社区负责现场值班值守的概率分别为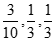 .
.
X的所有可能取值为0,1,2,3.
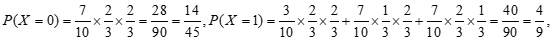
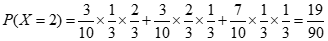
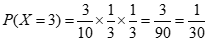
X的分布列为:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
……………………11分
(III) 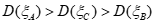 ……………………14分
……………………14分
19.(本小题共15分)
解:(I)因为f(x)=(x+a)lnx-x+1,
所以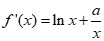 .
.
由题知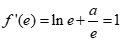 ,
,
解得a=0. …………………………4分
(II)当a=0时,f(x)=xlnx-x+1,
所以f’(x)=lnx.
当x∈(0,1)时,f’(x)<0,f(x)在区间(0,1)上单调递减;
当x∈(1,+∞)时,f’(x)>0,f(x)在区间(1,+∞)上单调递增;
所以f(1)=0是f(x)在区间(0,+∞)上的最小值.
所以f(x)≥0. …………………………8分
(II) 由(I)知,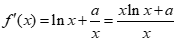
若a≥0,则当x∈(1,+∞)时, f’(x)>0,f(x)在区间(1,+∞)上单调递增,此时无极值.
若a<0,令g(x)= f’(x),
则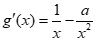 .
.
因为当x∈(1,+∞)时,g’(x)>0, 所以g(x)在(1,+∞)上单调递增.
因为g(1)=a<0,
而g(e-a)=-a+aea=a(ea-1)>0,
所以存在x0∈(1,e-a),使得g(x0)=0.
f’(x)和f(x)的情况如下:
x | (1,x0) | x0 | (x0,1-a) |
f'(x) | – | 0 | + |
f(x) | ↘ | 极小值 | ↗ |
因此,当x=x0时,f(x)有极小值f(x0).
综上,a的取值范围是(-∞,0). ……………………15分
20.(本小题共14分)
解:(I)由题意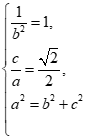
解得a2=2,b2=1.
所以椭圆C的方程为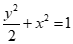 . …………………………5分
. …………………………5分
(II)假设存在点Q使得∠OQN +∠OQM =
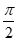 .设Q(m,0),
.设Q(m,0),
因为∠OQN+∠OQM =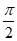 ,
,
所以∠OQN=∠OMQ.则tan∠OQN=tan∠OMQ.
即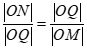 ,所以|OQ| 2=|ON|OM|.
,所以|OQ| 2=|ON|OM|.
因为直线y=y0交椭圆C于A,B两点,则A,B两点关于y轴对称.
设A(x0,y0),B(-x0,y0) (x0≠±1),
因为P(1,0),
则直线PA的方程为: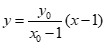 .
.
令x=0,得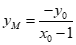 .
.
直线PB的方程为: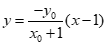 .
.
令x=0,得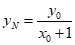 .
.
因为|OQ| 2=|ON|OM|,
所以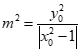
又因为点A(x0,y0)在椭圆C上,
所以y 02=2(1-x02).
所以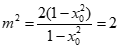 .即
.即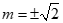 .
.
所以存在点Q
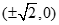 使得∠OQN +∠OQM =
使得∠OQN +∠OQM =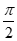 成立. ……………………14.分
成立. ……………………14.分
21. (本小题共14分)
解:(I)①1,1,1,1,1;
②1,0,0,0,1. ……………………4分
(II)(i)由题意,存在k∈{1,2,…,n-1}, 使得bk=bk+1=1.
若k=1,即b1=b2=1时,c1=c2=0.
于是bn=b2=1,b1=b3=1.
所以cn=c3=0,所以b4=b2=1.即b2=b3=b4=1.
依次类推可得bk=bk+1=1(k=2,3,…,n-1).
所以bk=1(k= 1,2,…,n).
若2≤k≤n-1,由bk=bk+1=1得ck=ck+1=0.
于是bk-1=bk+1=bk=1.所以ck-1=ck=0.
依次类推可得b1=b2=1.
所以bk=1(k =1,2,…,n).
综上可知,数列B中的每一项均为1. …………………………8分
(ii)首先证明不可能存在k∈{2,…,n-1}使得bk-1=bk=bk+1=0
若存在k∈{2,…,n-1}使得bk-1=bk=bk+1=0,
则ck-1=ck=ck+1=1.
又bk-1=bk+1得ck=0与已知矛盾.
所以不可能存在bk-1=bk=bk+1=0,k∈{2,…,n-1}.
由此及(i)得数列{bn}的前三项b1,b2,b3的可能情况如下:
(1)b1=b2=b3=1时,由(i)可得bk=1(k=1,2,…,n).
于是ck =0(k=1,2,…,n).
所以所有项的和S=0.
(2)b1=1,b2 =0,b3=1时,c2 =0,
此时b2 +c2=0与已知矛盾.
(3)b1=1,b2=0,b3=0时,c1=0,c2=1,c3=1.
于是bn=b2=0,b2≠b4=1.
故cn=1,c4=0,b5=b3=0
于是b1≠bn-1=0,c5=1,b6=0,
于是b1=b4,b2=b5,b3=b6,且bn-2=1,bn-1=0,bn=0.
依次类推bk=bk+3且n恰是3的倍数满足题意.
所以所有项的和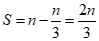 .
.
同理可得b1=0,b2=1,b3=0及b1=0,b2=0,b3=1时,
当且仅当n恰是3的倍数时,满足题意.
此时所有项的和S=
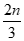 .
.
综上,所有项的和S=0或S=
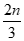 (n是3的倍数)…………………………14分
(n是3的倍数)…………………………14分
(若用其他方法解题,请酌情给分)