本试卷共150分。考试时长120分钟。
第一部分(选择题
共40分)
一、本大题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 已知集合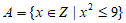 ,
,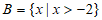 ,则
,则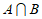 =
=
A. 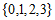 B.
B. 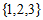 C.
C. 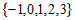 D.
D.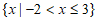
2. 已知复数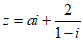 ,其所对应的点在第四象限,则实数a的取值范围是
,其所对应的点在第四象限,则实数a的取值范围是
A. 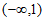 B.
B. 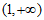 C.
C. 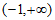 D.
D.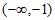
3. 要得到函数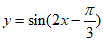 的图象,只需将函数
的图象,只需将函数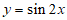 的图象
的图象
A. 向左平移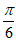 个单位长度 B. 向右平移
个单位长度 B. 向右平移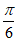 个单位长度
个单位长度
C. 向左平移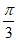 个单位长度 D. 向右平移
个单位长度 D. 向右平移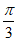 个单位长度
个单位长度
4. 某三棱柱的三视图如图所示,该三棱柱的体积为
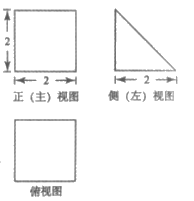
A. 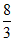 B.
B. 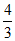 C. 8 D. 4
C. 8 D. 4
5. 在△ABC中,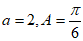 ,则”
,则”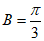 “是”
“是”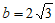 “的
“的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
6. 若直线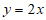 与双曲线
与双曲线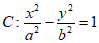 无公共点,则双曲线C的离心率可能是
无公共点,则双曲线C的离心率可能是
A. 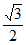 B. 1 C. 2 D.
B. 1 C. 2 D.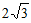
7.”苏州码子“发源于苏州,在明清至民国时期,作为一种民间的数字符号曾经流行一时,广泛应用于各种商业场合。110多年前,詹天佑主持修建京张铁路,首次将“苏州码子”刻于里程碑上,”苏州码子”计数方式如下: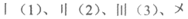
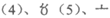
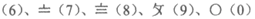 。为了防止混淆,有时要将
。为了防止混淆,有时要将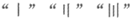 横过来写。已知某铁路的里程碑所刻数字代表距离始发车站的里程,每隔2公里摆放一个里程碑,若在A点处里程碑上刻着“
横过来写。已知某铁路的里程碑所刻数字代表距离始发车站的里程,每隔2公里摆放一个里程碑,若在A点处里程碑上刻着“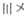 “,在B点处里程碑刻着”
“,在B点处里程碑刻着”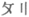 “,则从A点到B点里程碑的个数应为
“,则从A点到B点里程碑的个数应为
A. 29 B. 30 C. 58 D. 59
8. 记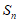 为等比数列
为等比数列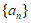 的前n项和,已知
的前n项和,已知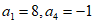 ,则数列
,则数列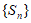
A. 有最大项,有最小项 B. 有最大项,无最小项
C. 无最大项,有最小项 D. 无最大项,无最小项
9. 在平面直角坐标系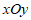 中,点
中,点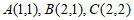 ,P是圆
,P是圆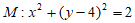 上一点,Q是△ABC边上一点,则
上一点,Q是△ABC边上一点,则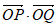 的最大值是
的最大值是
A. 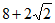 B. 12 C.
B. 12 C. 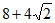 D. 16
D. 16
10. 甲乙丙三个学生同时参加了若干门学科竞赛(至少包含数学和物理),在每科竞赛中,甲乙丙三人中都有一个学生的分数为x,另一个学生的分数为y,第三个学生的分数为z,其中x,y,z是三个互不相等的正整数,在完成所有学科竞赛后,甲的总分为47分,乙的总分为24分,丙的总分为16分,且在甲乙丙这三个学生中乙的数学竞赛成绩排名第一,则
A. 甲乙丙三个学生至少参加了四门学科竞赛
B. x,y,z这三个数中的最大值可以取到21
C. 在甲乙丙这三个学生中,甲的物理竞赛成绩可能排名第二
D. 在甲乙丙这三个学生中,丙的物理竞赛成绩一定排名第二
第二部分(非选择题
共110分)
二、填空题:共5小题,每小题5分,共25分。
11. 已知向量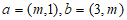 ,若a与b方向相反,则m等于___________。
,若a与b方向相反,则m等于___________。
12. 在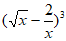 的展开式中,常数项是__________。
的展开式中,常数项是__________。
13. 对于抛物线C,给出下列三个条件:
①对称轴为y轴;②过点(1,1);③焦点到准线的距离为2。
写出符合其中两个条件的一个抛物线C的标准方程____________________。
14. 共享单车已经成为方便人们出行的交通工具,某公司决定从2020年1月开始向某地投放共享单车,记第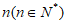 个月共享单车的投放量和损失量分别为an和bn(单位:千辆),其中a1=1,b1=0.1,从第2个月到2021年12月,共享单车的每月投放量比上个月增加1千辆,从2022年1月开始,共享单车的每月投放量比上个月减少1千辆;根据预测,从2020年1月开始,共享单车的每月损失量比上个月增加100辆,设第n个月底的共享单车的保有量是前n个月的累计投放量与累计损失量的差,则该地区第4个月底的共享单车的保有量为__________千辆;当n为___________时,该地区第n个月底的共享单车保有量达到最大。
个月共享单车的投放量和损失量分别为an和bn(单位:千辆),其中a1=1,b1=0.1,从第2个月到2021年12月,共享单车的每月投放量比上个月增加1千辆,从2022年1月开始,共享单车的每月投放量比上个月减少1千辆;根据预测,从2020年1月开始,共享单车的每月损失量比上个月增加100辆,设第n个月底的共享单车的保有量是前n个月的累计投放量与累计损失量的差,则该地区第4个月底的共享单车的保有量为__________千辆;当n为___________时,该地区第n个月底的共享单车保有量达到最大。
15. 已知函数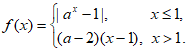 其中
其中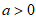 且
且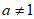 。给出下列四个结论:
。给出下列四个结论:
①若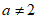 ,则函数
,则函数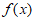 的零点是0;
的零点是0;
②若函数f(x)无最小值,则a的取值范围为(0,1);
③若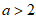 ,则
,则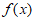 在区间
在区间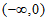 上单调递减,在区间
上单调递减,在区间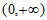 上单调递增;
上单调递增;
④若关于x的方程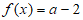 恰有三个不相等的实数根
恰有三个不相等的实数根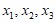 ,则a的取值范围为(2,3),且
,则a的取值范围为(2,3),且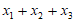 的取值范围为
的取值范围为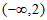 。
。
其中,所有正确结论的序号是________________。
三、解答题:共6小题,共85分。解答应写出文字说明,演算步骤或证明过程。
16. (本小题13分)
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB∥CD,AB⊥AD,AB=4,PA=AD=CD=2,点E为PB的中点。
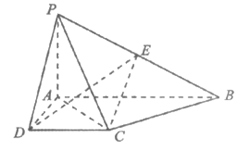
(Ⅰ)求证:平面PBC⊥平面PAC;
(Ⅱ)求二面角E-CD-A的余弦值。
17. (本小题13分)
已知函数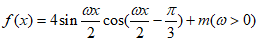 ,在下列条件①、条件②、条件③这三个条件中,选择可以确定ω和m值的两个条件作为已知。
,在下列条件①、条件②、条件③这三个条件中,选择可以确定ω和m值的两个条件作为已知。
(Ⅰ)求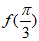 的值;
的值;
(Ⅱ)若函数f(x)在区间[0,a]上是增函数,求实数a的最大值。
条件①:f(x)最小正周期为π;
条件②:f(x)最大值与最小值之和为0;
条件③:f(0)=2。
注:如果选择多组条件分别解答,按第一个解答计分。
18.(本小题14分)
在新冠病毒疫情防控期间,北京市中小学开展了“优化线上教育与学生线下学习相结合”的教育教学实践活动,为了解某区教师对A,B,C,D,E五类线上教育软件的使用情况(每位教师都使用这五类教育软件中的某一类且每位教师只选择一类教育软件),从该区教师中随机抽取了100人,统计数据如下表,其中a>b,a、b∈N。
教育软件类型 | A | B | C | D | E |
选用教师人数 | 10 | 15 | a | 30 | b |
假设所有教师选择使用哪类软件相互独立。
(Ⅰ)若某校共有300名教师,试估计该校教师中使用教育软件C或E的人数;
(Ⅱ)从该区教师中随机抽取3人,估计这3人中至少有2人使用教育软件D的概率;
(Ⅲ)设该区有3000名教师,从中随机抽取1人,记该教师使用教育软件C或D的概率估计值为P1;该区学校M有600名教师,其中有200人使用教育软件C,100人使用教育软件D,从学校M中随机抽取1人,该教师使用教育软件C或D的概率值为P2;从该区其他教师(除学校M外)中随机抽取1人,该教师使用教育软件C或D的概率估计值为P3,试比较P1,P2和P3之间的大小。(结论不要求证明)
19.(本小题15分)
已知椭圆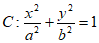 的离心率为
的离心率为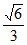 ,其长轴的两个端点分别为
,其长轴的两个端点分别为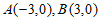 。
。
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)点P为椭圆上除A,B外的任意一点,直线AP交直线x=4于点E,点O为坐标原点,过点O且与直线BE垂直的直线记为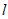 ,直线BP交y轴于点M,交直线
,直线BP交y轴于点M,交直线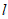 于点N,求△BMO与△NMO的面积之比。
于点N,求△BMO与△NMO的面积之比。
20.(本小题15分)
已知函数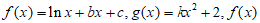 在
在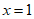 处取得极大值1。
处取得极大值1。
(Ⅰ)求b和c的值;
(Ⅱ)当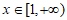 时,曲线
时,曲线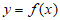 在曲线
在曲线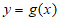 的上方,求实数k的取值范围。
的上方,求实数k的取值范围。
(Ⅲ)设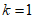 ,证明:存在两条与曲线
,证明:存在两条与曲线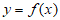 和
和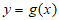 都相切的直线。
都相切的直线。
21.(本小题15分)
设A是正整数集的一个非空子集,如果对于任意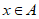 ,都有
,都有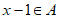 或
或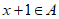 ,则称A为自邻集,记集合
,则称A为自邻集,记集合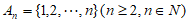 的所有子集中的自邻集的个数为
的所有子集中的自邻集的个数为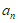 。
。
(Ⅰ)直接写出A4的所有自邻集;
(Ⅱ)若n为偶数且n≥6,求证:An的所有含5个元素的子集中,自邻集的个数是偶数;
(Ⅲ)若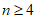 ,求证:
,求证: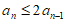 。
。
【试题答案】
一、选择题(共10小题,每小题4分,共40分)
1.C 2. D 3. B 4. D 5. A 6. C 7. B 8. A
9. B 10. D
二、填空题(共5小题,每小题5分,共25分)
11. 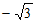 12. -6 13.
12. -6 13. 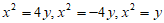 (以上答案均可)
(以上答案均可)
14. 9,43 15. ①④
注:第14题第一空3分,第二空2分,第15题全部选对得5分,不选或有错选得0分,其他得3分。
三、解答题(共6小题,共85分)
16.(共13分)
解:(Ⅰ)取AB的中点F,连接CF,所以AF=CD,
又因为AF∥CD,所以四边形AFCD是平行四边形。
因为AB⊥AD,AD=CD,所以四边形AFCD是正方形,
则AB⊥CF,CF=AD=2,所以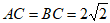 ,
,
得到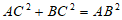 ,
,
所以BC⊥AC。 1分
因为PA⊥平面ABCD,
所以PA⊥BC, 2分
因为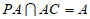 ,
,
所以BC⊥平面PAC, 3分
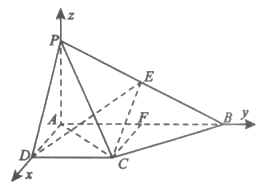
因为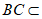 平面PBC, 4分
平面PBC, 4分
平面PBC⊥平面PAC。 5分
(Ⅱ)因为PA⊥平面ABCD,
所以PA⊥AD,PA⊥AB,则PA,AD,AB两两垂直,
如图建立空间直角坐标系A-xyz。 6分
则A(0,0,0),P(0,0,2),B(0,4,0),C(2,2,0),D(2,0,0),E(0,2,1),
所以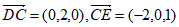 。
。
设平面CDE的法向量为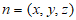 ,
,
所以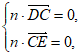
所以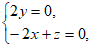
即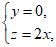 8分
8分
令x=1,则z=2,
所以平面CDE的法向量为n=(1,0,2), 9分
又因为平面ACD的法向量m=(0,0,1), 10分
所以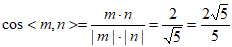 , 12分
, 12分
由已知,二面角E—CD—A为锐角,
所以二面角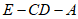 的余弦值为
的余弦值为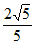 。 13分
。 13分
17.(共13分)
解:(Ⅰ)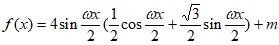 2分
2分
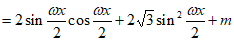
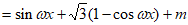 4分
4分
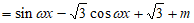
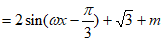 。 5分
。 5分
选择条件①②:
由条件①得,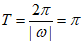 ,又因为
,又因为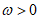 ,所以
,所以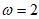 。 6分
。 6分
由②知,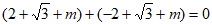 ,所以
,所以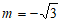 。 7分
。 7分
则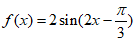 ,
,
所以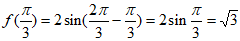 。 8分
。 8分
(Ⅱ)令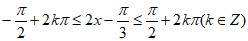 , 10分
, 10分
所以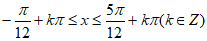 ,
,
所以函数f(x)的单调增区间为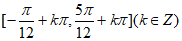 。 11分
。 11分
因为函数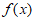 在
在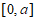 上单调递增,且
上单调递增,且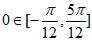 ,此时
,此时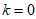 ,
,
所以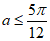 ,故实数a的最大值为
,故实数a的最大值为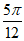 。 13分
。 13分
选择条件①③:
由条件①得,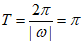 ,又因为
,又因为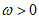 ,所以
,所以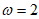 , 6分
, 6分
由③知,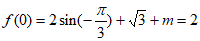 ,所以
,所以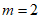 , 7分
, 7分
则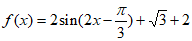 ,
,
所以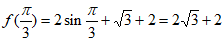 。 8分
。 8分
(Ⅱ)令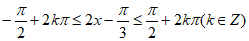 , 10分
, 10分
所以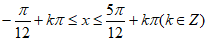 ,
,
所以函数f(x)的单调增区间为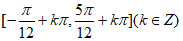 , 12分
, 12分
因为函数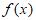 在
在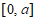 上单调递增,且
上单调递增,且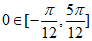 ,此时
,此时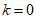 ,
,
所以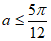 ,故实数a的最大值为
,故实数a的最大值为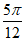 。 13分
。 13分
说明:不可以选择条件②③:
由②知,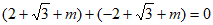 ,所以
,所以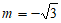 ;
;
由③知,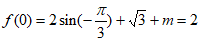 ,所以
,所以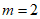 ;矛盾。
;矛盾。
所以函数f(x)不能同时满足条件②和③。
18.(共14分)
解:(Ⅰ)从表格数据可知,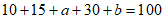 ,则
,则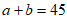 ,
,
所以样本中教师使用教育软件C或E的人数为45人, 2分
故估计该校教师中使用教育软件C或E的人数为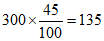 人。 4分
人。 4分
(Ⅱ)设事件F为“从该区教师中随机抽取3人,至少有2人使用教育软件D”。
由题意,样本中的100名教师使用软件D的频率为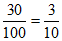 。
。
用频率估计概率,从该区教师中随机抽取一名教师,估计该教师使用教育软件D的概率为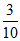 , 5分
, 5分
记被抽取的3人中使用软件D的人数为X,则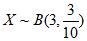 。 7分
。 7分
所以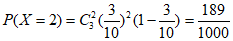 , 8分
, 8分
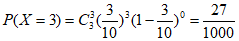 , 9分
, 9分
所以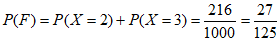 。 11分
。 11分
(Ⅲ)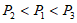 。 14分
。 14分
19.(共15分)
解:(Ⅰ)由题意,得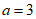 ,又
,又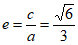 ,所以
,所以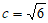 。 3分
。 3分
又因为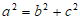 ,所以
,所以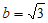 ,
,
故椭圆C的方程为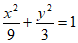 。 5分
。 5分
(Ⅱ)设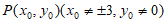 ,则
,则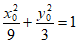 , 6分
, 6分
所以直线AP的方程为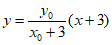 7分
7分
令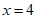 ,得点E的坐标为
,得点E的坐标为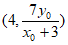 。 8分
。 8分
因为直线BE的斜率为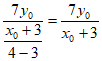 ,
,
所以直线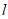 的方程为
的方程为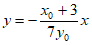 , 9分
, 9分
又因为直线PB的方程为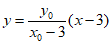 , 10分
, 10分
联立直线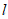 和直线PB的方程,消去y得
和直线PB的方程,消去y得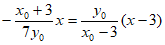 ,
,
所以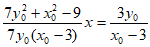 , 11分
, 11分
因为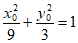 ,所以
,所以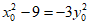 ,
,
所以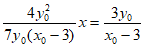 ,解得点N的横坐标
,解得点N的横坐标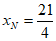 , 13分
, 13分
所以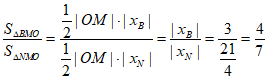 。 15分
。 15分
即△BMO与△NMO的面积之比为4:7。
20.(共15分)
解:(Ⅰ)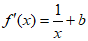 。 1分
。 1分
由已知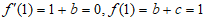 , 3分
, 3分
解得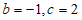 ,经检验,满足题意, 4分
,经检验,满足题意, 4分
所以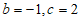 。
。
(Ⅱ)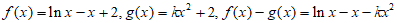 ,
,
依题意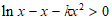 对任意的
对任意的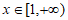 恒成立, 5分
恒成立, 5分
所以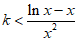 对任意的
对任意的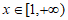 恒成立。
恒成立。
令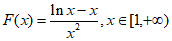 ,
,
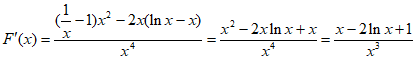 , 6分
, 6分
令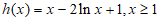 ,
,
所以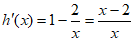 ,令
,令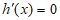 ,所以
,所以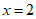 。 7分
。 7分
因为当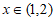 时,
时,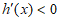 ,
,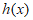 单调递减;
单调递减;
当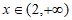 时,
时,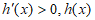 单调递增。
单调递增。
当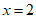 时,函数
时,函数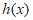 的最小值为
的最小值为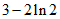 ,且
,且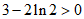 , 8分
, 8分
所以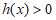 ,即
,即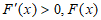 在
在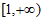 上单调递增,
上单调递增,
所以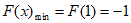 ,
,
所以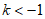 ,故实数k的取值范围为
,故实数k的取值范围为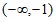 。 9分
。 9分
(Ⅲ)假设存在与曲线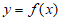 和曲线
和曲线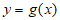 都相切的直线
都相切的直线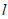 ,
,
设切点坐标分别为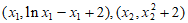 ,
,
因为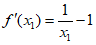 ,所以
,所以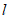 的方程为
的方程为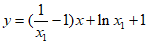 , 10分
, 10分
因为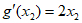 ,所以
,所以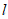 的方程为
的方程为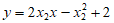 , 11分
, 11分
所以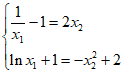 ,消去
,消去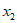 得
得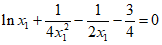 。
。
①
令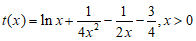 ,
,
所以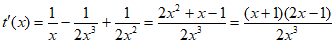 ,
,
所以,在区间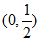 上,
上,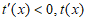 是减函数;在区间
是减函数;在区间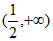 上,
上,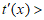 0,
0,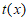 是增函数, 13分
是增函数, 13分
所以,当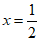 时,函数
时,函数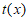 的最小值为
的最小值为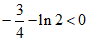 。
。
又因为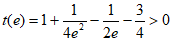 ,
,
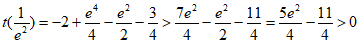 , 14分
, 14分
所以函数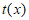 在
在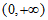 上有两个零点,即方程①有两个不等的正实根,
上有两个零点,即方程①有两个不等的正实根,
由方程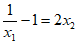 可得
可得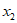 有两个不同的值,
有两个不同的值,
所以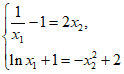 有两组不同的解,直线
有两组不同的解,直线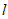 有两条, 15分
有两条, 15分
所以存在两条与曲线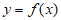 和
和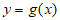 都相切的直线。
都相切的直线。
21.(共15分)
解:(Ⅰ)A4的子集中的自邻集有:
{1,2,3,4},{1,2,3},{2,3,4},{1,2},{2,3},{3,4}。 4分
(Ⅱ)对于集合An的含有5个元素的自邻集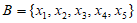 ,
,
不妨设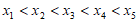 ,
,
因为对于任意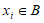 ,都有
,都有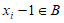 或
或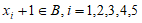 ,
,
所以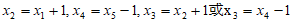 , 6分
, 6分
对于集合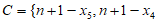 ,
,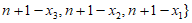 ,
,
因为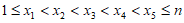 ,所以
,所以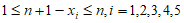 ,
,
且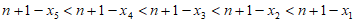 ,
,
所以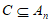 。 7分
。 7分
因为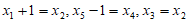 +1或
+1或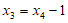 ,
,
所以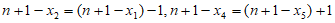 ,
,
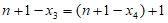 或
或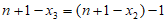 ,
,
所以,对于任意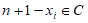 ,都有
,都有
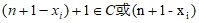
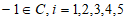 。
。
所以集合C也是自邻集。 8分
因为当n为偶数时,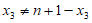 ,
,
所以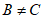 ,
,
所以,对于集合An任意一个含有5个元素的自邻集,在上述对应方法下会存在一个不同的含有5个元素的自邻集与其对应。
所以,An的含有5个元素的自邻集的个数为偶数。 9分
(Ⅲ)记自邻集中最大元素为k的自邻集的个数为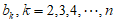 。
。
当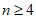 时,
时,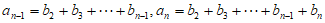 ,
,
显然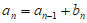 。 11分
。 11分
下面证明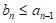 ,
,
①自邻集中含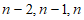 这三个元素,
这三个元素,
记去掉这个自邻集中的元素n后的集合为D,因为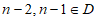 ,所以D仍然是自邻集,且集合D中的最大元素是
,所以D仍然是自邻集,且集合D中的最大元素是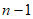 ,所以含
,所以含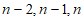 这三个元素的自邻集的个数为
这三个元素的自邻集的个数为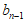 。 12分
。 12分
②自邻集中含有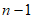 ,n这两个元素,不含
,n这两个元素,不含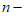 2,且不只有
2,且不只有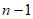 ,n两个元素,
,n两个元素,
记自邻集中除n,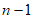 之外的最大元素为m,则
之外的最大元素为m,则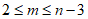 ,
,
每个自邻集去掉n-1,n这两个元素后,仍然为自邻集,
此时的自邻集的最大元素为m,可将此时的自邻集分为n-4类:
含最大数为2的集合个数为b2,
含最大数为3的集合个数为b3。
……
含最大数为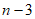 的集合个数为
的集合个数为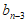 。
。
则这样的集合共有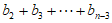 个。 13分
个。 13分
③自邻集只含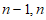 两个元素,这样的自邻集只有1个。 14分
两个元素,这样的自邻集只有1个。 14分
综上可得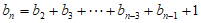
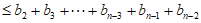
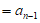 ,
,
所以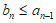 ,
,
所以当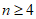 时,
时,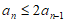 。 15分
。 15分
