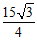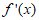本试卷150分,考试时长120分钟。
第一部分(选择题
共40分)
一、选择题:共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
(1)在平面直角坐标系xOy中,角θ以Ox为始边,终边经过点(-3,4),则cosθ=
(A) 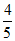 (B)
(B) 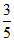 (C)
(C)  (D)
(D)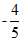
(2)设a∈R.若(2+i)(a-i)=-1-3i,则a=
(A)-1 (B) -2 (C)1 (D)2
(3)已知a=0.31.5,b=log1.50.3,c=1.50.3,则
(A)a<b<c (B)b<a<c
(C)a<c<b (D)b<c<a
(4)已知F为抛物线y2=4x的焦点,P(x0,y0)是该抛物线上的一点,若|PF|>2,则
(A) x0∈ (0,1) (B) x0∈(1,+∞)
(C) y0∈(2,+∞) (D) y0∈(-∞,2)
(5)向量a,b,c在边长为l的正方形网格中的位置如图所示.若e为与c同方向的单位向量,则 (a+b)·e=
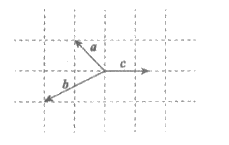
(A)1.5 (B) 2 (C) -4.5 (D) -3
(6)已知实数x,y满足x2+y2+4x-6y+12=0,则x的最大值是
(A)3 (B)2 (C) -1 (D) -3
(7)已知指数函数f(x)=ax,将函数f(x)的图象上的每个点的横坐标不变,纵坐标扩大为原来的3倍,得到函数g(x)的图象,再将g(x)的图象向右平移2个单位长度,所得图象恰好与函数f(x)的图象重合,则a的值是
(A) 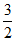 (B)
(B) 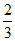 (C)
(C) 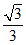 (D)
(D)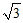
(8)已知正方体ABCD-A1B1C1D1(如图1),点P在侧面CDD1C1内(包括边界).若三棱锥B1-ABP的俯视图为等腰直角三角形(如图2),则此三棱锥的左视图不可能是
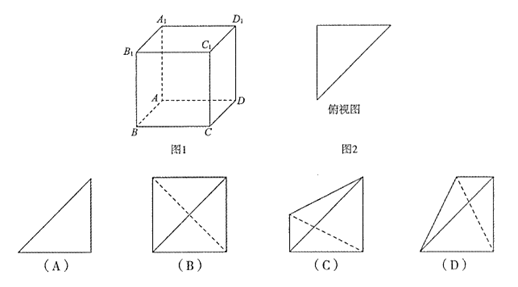
(9)已知实数α,β.“α+β=2kπ,k∈Z“是“sin(α+β)=sinα+sinβ”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(10)已知函数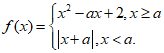 若对于任意正数k,关于x的方程f(x)=k都恰有两个不相等的实数根,则满足条件的实数a的个数为
若对于任意正数k,关于x的方程f(x)=k都恰有两个不相等的实数根,则满足条件的实数a的个数为
(A)0 (B)1 (C)2 (D)无数
第二部分(非选择题
共110分)
二、填空题:共5小题,每小题5分,共25分。
(11)已知数列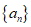 满足a1=2,an+1-2an=0(n=1,2,…),则
满足a1=2,an+1-2an=0(n=1,2,…),则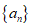 的前6项和为__________.
的前6项和为__________.
(12)已知(1+2x)n的展开式的二项式系数之和为16,则n=___________;各项系数之和为_________.
(用数字作答)
(13)在△ABC中,a=3,b=7,∠B=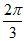 ,则△ABC的面积为_________.
,则△ABC的面积为_________.
(14)已知双曲线M: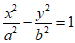 的左焦点为F1,A,B为双曲线M上的两点,O为坐标原点,若四边形F1ABO为菱形,则双曲线M的离心率为_________.
的左焦点为F1,A,B为双曲线M上的两点,O为坐标原点,若四边形F1ABO为菱形,则双曲线M的离心率为_________.
(15)普林斯顿大学的康威教授于1986年发现了一类有趣的数列并命名为“外观数列“(Look and say sequence),该数列的后一项由前一项的外观产生.以i(i∈N,0≤i≤9)为首项的“外观数列“记作Ai,其中A1,为1,11,21,1211,111221,…,即第一项为1,外观上看是1个1,因此第二项为11;第二项外观上看是2个1,因此第三项为21;第三项外观上看是1个2,1个1,因此第四项为1211,….按照相同的规则可得其它Ai,例如A3为3,13,1113,3113,132113,….给出下列四个结论:
①若Ai的第n项记作an,Aj的第n项记作bn,其中2≤i<j≤9,则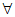 n∈N*,an-bn=i-j;
n∈N*,an-bn=i-j;
②A1中存在一项,该项中某连续三个位置上均为数字3;
③A1的每一项中均不含数字4;
④对于k≥2,i≠1,Ai的第k项的首位数字与A1的第k+2项的首位数字相同.
其中所有正确结论的序号是_________.
三、解答题:共6小题,共85分。解答应写出文字说明、演算步骤或证明过程。
(16)(本小题共14分)
如图,在三棱锥P-ABC中,BC⊥AC,BC⊥PC,AC=BC=6,PA =PC=5,D,E分别是AC,PC的中点.
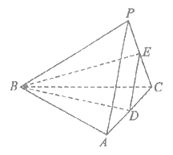
(I)求证:平面PAC⊥平面ABC;
(Ⅱ)求二面角A-DE-B的余弦值.
(17)(本小题共14分)
已知函数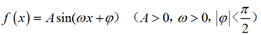 的部分图象如图所示.
的部分图象如图所示.
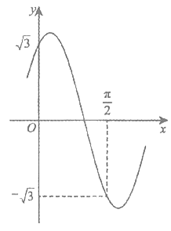
(I)直接写出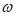 的值;
的值;
(Ⅱ)再从条件①、条件②中选择一个作为已知,求函数f(x)在区间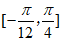 上的最小值.
上的最小值.
条件①:直线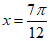 为函数y=f(x)的图象的一条对称轴;
为函数y=f(x)的图象的一条对称轴;
条件②:(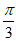 ,0)为函数y=f(x)的图象的一个对称中心.
,0)为函数y=f(x)的图象的一个对称中心.
(18)(本小题共14分)
为迎接2022年北京冬季奥运会,普及冬奥知识,某地区小学联合开展了“冰雪答题王“冬奥知识竞赛活动.现从参加该活动的学生中随机抽取了30名学生,将他们的竞赛成绩(单位:分)用茎叶图记录如下:
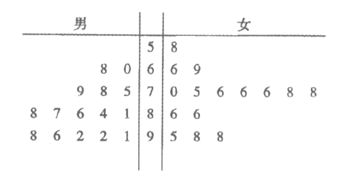
(I)从该地区参加该活动的男生中随机抽取1人,估计该男生的竞赛成绩在90分以上的概率;
(Ⅱ)从该地区参加该活动的全体男生中随机抽取2人,全体女生中随机抽取2人,估计这4人中男生竞赛成绩在90分以上的人数比女生竞赛成绩在90分以上的人数多的概率;
(Ⅲ)为便于普及冬奥知识,现从该地区某所小学参加冬奥知识竞赛活动的学生中随机选取10名男生、10名女生作为冬奥宣传志愿者.记这10名男生竞赛成绩的平均数为μ1,这10名女生竞赛成绩的平均数为μ2,能否认为μ1>μ2,说明理由.
(19)(本小题共14分)
椭圆C: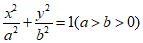 的左、右焦点分别为F1, F2,E是椭圆C上一点,且|F1F2|=2,|EF1|+|EF2|=4.
的左、右焦点分别为F1, F2,E是椭圆C上一点,且|F1F2|=2,|EF1|+|EF2|=4.
(I)求椭圆C的方程;
(Ⅱ)M,N是y轴上的两个动点(点M与点E位于x轴的两侧),∠MF1N=∠MEN=90°,直线EM交x轴于点P,求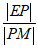 的值.
的值.
(20)(本小题共15分)
已知函数f(x) =x-alnx.
(I)求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)若关于x的方程x-alnx=0有两个不相等的实数根,记较小的实数根为x0,求证:(a-1)x0>a.
(21)(本小题共14分)
已知有限集X,Y,定义集合X-Y= {x|x∈X,且x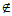 Y},|X|表示集合X中的元素个数.
Y},|X|表示集合X中的元素个数.
(I)若X={1,2,3,4),Y={3,4,5},求集合X-Y和Y-X,以及|(X-Y)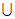 (Y-X)|的值;
(Y-X)|的值;
(Ⅱ)给定正整数n,集合S={1,2,…,n}.对于实数集的非空有限子集A,B,定义集合C={x|x=a+b,a∈A,b∈B}.
①求证:|A-S|+|B-S|+|S-C|≥1;
②求|(A-S)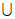 (S-A )|+|(B-S)
(S-A )|+|(B-S)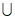 (S-B)|+|(C-S)
(S-B)|+|(C-S) (S-C)|的最小值.
(S-C)|的最小值.
参考答案
一、选择题:共10小题,每小题4分,共40分。
题号 | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
答案 | C | A | B | B | D | C | D | D | A | B |
二、填空题:共5小题,每小题5分,共25分。
题号 | (11) | (12) | (13) | (14) | (15) |
答案 | 126 | 4 81 |
4 |
| ①③④ |
三、解答题共6小题,共85分。
(16)(本小题共14分)
解:(I)因为BC⊥PC,AC⊥BC,AC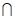 PC =C,AC
PC =C,AC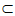 平面PAC,PC
平面PAC,PC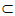 平面PAC,
平面PAC,
所以BC⊥平面PAC.
又因为BC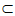 平面ABC,
平面ABC,
所以平面ABC⊥平面PAC.
( II)连结PD,因为PA= PC,D是AC的中点,
所以AD= DC,PD⊥AC.
过C作CH∥PD,则CH⊥AC.
因为BC⊥平面PAC,CH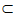 平面PAC,
平面PAC,
所以BC⊥CH,
又BC⊥AC,
如图,以C为原点,分别以CB,CA,CH所在直线为x轴,y轴,z轴建立空间直角坐标系C—xyz,
因为AC=6,PC =5,
所以PD=4.
因为BC =6,
所以C(0,0,0),B(6,0,0),A(0,6,0),D(0,3,0),P(0,3,4).
因为E是PC的中点,
所以E(0,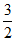 ,2).
,2).
所以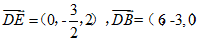 .
.
设平面DEB的法向量为n=(x,y,z),
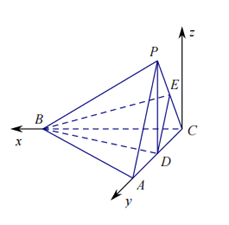
则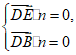 即
即
令x= -2,则y=-4,z=-3.
所以n= (-2,-4,-3).
由( I)可得:BC⊥平面PAC.
取平面ADE的一个法向量为
m=(1,0,0).
所以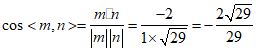
所以二面角A-DE-F的余弦值为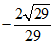 .
.
(17)(本小题共14分)
解:(I) 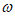 =2.
=2.
(II)选择条件①
因为直线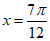 为函数
为函数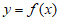 的图象的一条对称轴,
的图象的一条对称轴,
所以
当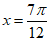 时,
时,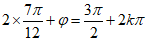 ,k∈Z,
,k∈Z,
即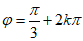 ,k∈Z.
,k∈Z.
因为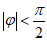 ,
,
所以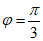 .
.
因为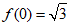 ,
,
所以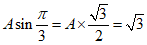 .
.
所以A=2.
所以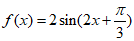 .
.
因为当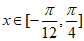 时,
时,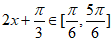
所以当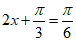 或
或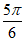 时,即当
时,即当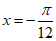 或
或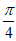 时,
时,
f(x)取到最小值,最小值为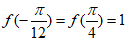 .
.
选择条件②
因为(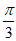 ,0)为函数
,0)为函数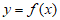 的图象的一个对称中心,
的图象的一个对称中心,
所以当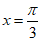 时,
时,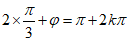 ,k∈Z,
,k∈Z,
即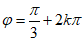 ,k∈Z.
,k∈Z.
因为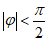 ,
,
所以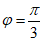 .
.
因为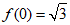 ,
,
所以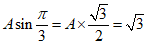 .
.
所以A=2.
所以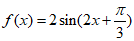 ,
,
因为当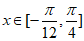 时,
时,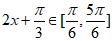
所以当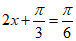 或
或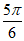 时,即当
时,即当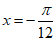 或
或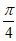 时,
时,
f(x)取到最小值,最小值为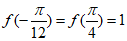 .
.
(18)(本小题共14分)
解:(I)由茎叶图可知,随机抽取的30名学生中男生有15名,其中竞赛成绩在90分以上的学生有5名,
所以随机抽取的15名男生中竞赛成绩在90分以上的频率为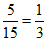 .
.
所以从该地区参加该活动的男生中随机抽取1人,该男生的竞赛成绩在90分以上的概率估计为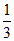 .
.
(II)记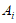 (i=1,2)表示“第i名男生的竞赛成绩在90分以上“,Bj(j=l,2)表示“第j名女生的竞赛成绩在90分以上“,C表示“4人中男生竞赛成绩在90分以上的人数比女生竞赛成绩在90分以上的人数多“.
(i=1,2)表示“第i名男生的竞赛成绩在90分以上“,Bj(j=l,2)表示“第j名女生的竞赛成绩在90分以上“,C表示“4人中男生竞赛成绩在90分以上的人数比女生竞赛成绩在90分以上的人数多“.
同(I),从该地区参加该活动的女生中随机抽取1人,该女生竞赛成绩在90分以上的概率估计为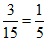 ,则
,则
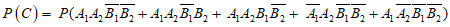
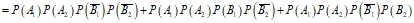
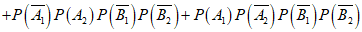
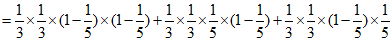
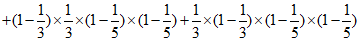
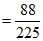
(III)参考答案:不能确定是否有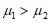 ,
,
上述10名男生,10名女生竞赛成绩的数据是随机的,所以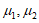 是随机的,
是随机的,
所以不能确定是否有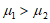 .
.
(19)(本小题共14分)
解:(I)由题意知: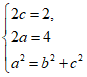
解得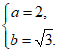
所以椭圆C的方程为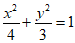 .
.
(II)设M(0,m),N(0,n),E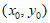 .由(I)可知F1(-l,0),F2(1,0).
.由(I)可知F1(-l,0),F2(1,0).
因为∠MF1N=90°,
所以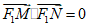 ,即
,即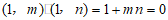 .
.
所以mn= -1.
又因为∠MEN=90°,
所以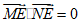 ,即
,即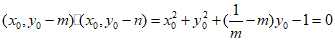 .
.
又因为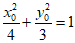 ,
,
所以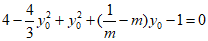 .
.
所以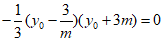 .
.
所以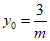 或
或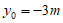 .
.
因为点M与点E位于x轴的两侧,即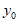 与m异号,
与m异号,
所以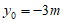 .
.
所以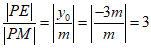 .
.
(20)(本小题共15分)
解:(I)因为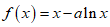 ,
,
所以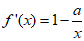 .
.
所以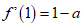 ,
,
又因为f(1)=1,
所以曲线y=f(x)在点(1,f(1))处的切线方程为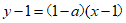 ,即
,即
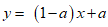 .
.
(II)f(x)的定义域为(0,+∞).
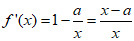
当a≤0时,f'(x)>0,所以f (x)的单调递增区间为(0,+∞).
当a>0时,令f'(x)=0,得x=a.
f(x)与f'(x)在区间(0,+∞)上的情况如下:
x | (0,a) | a | (a,+∞) |
| – | 0 | + |
f(x) | ↘ | 极小值 | ↗ |
所以f(x)的单调递减区间为(0,a),单调递增区间为(a,+∞).
(III)由(II)知:
①当a≤0时,f (x)在(0,+∞)上单调递增,
所以f(x)=0至多有一个实根,不符合题意.
②当a>0时,f(x)在(0,a)上单调递减,在(a,+∞)上单调递增,
所以f(x)的最小值为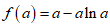 .
.
若f(a)≥0,则f(x)≥0,所以f(x)=0至多有一个实根,不符合题意,
若f(a)<0,即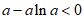 ,得a>e.
,得a>e.
又f(1)=1>0,且f (x)在(0,a)上单调递减,
所以f(x)在(0,a)上有唯一零点.
因为方程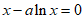 有两个不相等的实数根,且较小的实数根为x0,
有两个不相等的实数根,且较小的实数根为x0,
所以f(x)在(0,a)上的唯一零点就是x0.
方法一:
所以 .
.
所以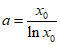 .
.
所以“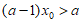 “等价于“
“等价于“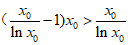 “,即
“,即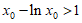 .
.
由(II)知,当a=l时,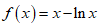 的最小值为f(1)=1.
的最小值为f(1)=1.
又因为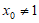 ,所以
,所以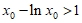 .
.
所以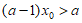 .
.
方法二:
“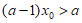 “等价于“
“等价于“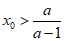 ”
”
又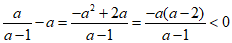 ,
,
所以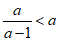 .
.
因为f(x)在(0,a)上单调递减,
所以“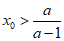 “等价于“
“等价于“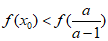 “,
“,
即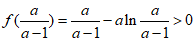 (*)
(*)
因为a>e,
令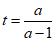 ,则t>l,
,则t>l,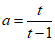 .
.
即(*)等价于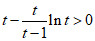 ,即
,即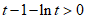 .
.
所以“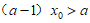 “等价于“
“等价于“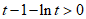 “.
“.
令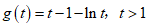 .
.
所以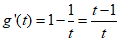 .
.
当t>l时,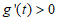 ,所以g(t)在(1,+∞)上单调递增,
,所以g(t)在(1,+∞)上单调递增,
所以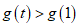 ,而g(1)=0.
,而g(1)=0.
所以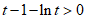 成立.
成立.
所以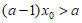 .
.
(21)(本小题共14分)
解:(I) 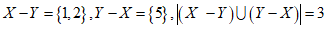 .
.
(II)①显然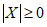 .
.
若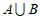 中含有一个不在S中的元素,则
中含有一个不在S中的元素,则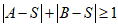 ,即
,即
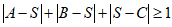 .
.
若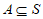 ,且
,且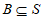 ,则
,则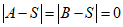 .
.
此时A中最小的元素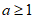 ,B中最小的元素
,B中最小的元素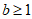 ,
,
所以C中最小的元素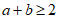 .
.
所以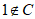 .
.
因为S={1,2,…,n},
所以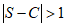 ,即
,即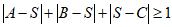 .
.
综上,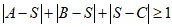 .
.
②由①知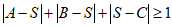 .
.
所以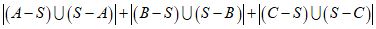
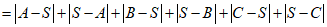
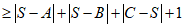 .
.
若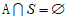 ,或
,或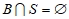 ,则
,则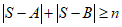 .
.
若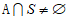 ,且
,且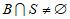 ,设
,设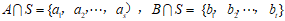 ,
,
且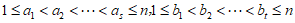 ,
,
则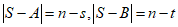 .
.
若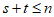 ,则
,则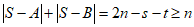 .
.
若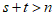 ,
,
因为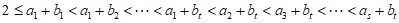 ,
,
所以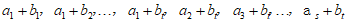 这
这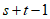 个数一定在集合C中,且均不等于1.
个数一定在集合C中,且均不等于1.
所以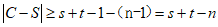 .
.
所以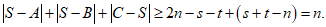
所以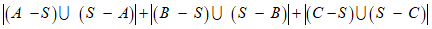
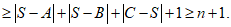
当A=B=S,C={2,3,…,2n}时,
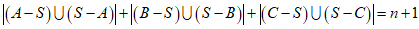 .
.
所以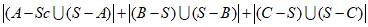 的最小值是
的最小值是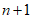 .
.