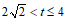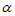本试卷共三道大题,28道小题,满分100分。考试时间120分钟。
一、选择题(本题共16分,每小题2分)
第1-8题均有四个选项,符合题意的选项只有一个。
1. 下图是某几何体的三视图,该几何体是(
)
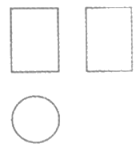
A. 圆柱 B. 球 C. 三棱柱 D. 长方体
2. 2021年2月24日6时29分,我国自主研制的首个火星探测器“天问一号“成功实施第三次近火制动,进入近火点280千米、远火点59000千米、周期2个火星日的火星停泊轨道。将59000用科学记数法表示应为(
)
A. 0.59×105 B. 5.9×105 C. 5.9×104 D. 5.9×103
3. 七巧板是我国的一种传统智力玩具。下列用七巧板拼成的图形中,是轴对称图形的是(
)
A.  B.
B.  C.
C. 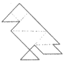 D.
D.
4. 如图是一个可以自由转动的转盘,转盘分成4个大小相同的扇形,颜色分为灰、白二种颜色。指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),则指针指向白色区域的概率是(
)
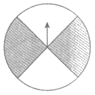
A. 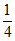 B.
B. 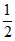 C.
C. 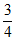 D. 1
D. 1
5. 若正多边形的一个外角是60°,则该正多边形的边数是(
)
A. 3 B. 4 C. 5 D. 6
6. 实数a与b在数轴上对应点的位置如图所示,则正确的结论是(
)
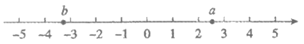
A. a<0 B. a<b C. b+5>0 D. |a|>|b|
7. 已知x=1是不等式2x-b<0的解,b的值可以是(
)
A. 4 B. 2 C. 0 D. -2
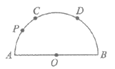
8. 如图,AB是⊙O直径,点C,D将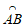 分成相等的三段弧,点P在
分成相等的三段弧,点P在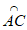 上。已知点Q在
上。已知点Q在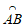 上且∠APQ=115°,则点Q所在的弧是(
上且∠APQ=115°,则点Q所在的弧是(
)
A. 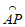 B.
B. 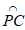 C.
C. 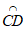 D.
D.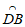
二、填空题(本题共16分,每小题2分)
9. 若代数式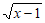 有意义,则实数x的取值范围是________。
有意义,则实数x的取值范围是________。
10. 方程组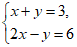 的解为________。
的解为________。
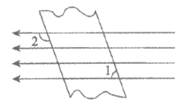
11. 如图,在一束平行光线中插入一张对边平行的纸板。如果图中∠1是70°,那么∠2的度数是________。
12. 若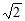 +a的值为有理数,请你写出一个符合条件的实数a的值_________。
+a的值为有理数,请你写出一个符合条件的实数a的值_________。
13. 计算:(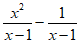 )·
)·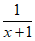 =________。
=________。
14. 已知关于x的方程x2–(m+2)x+4=0有两个相等的实数根,则m的值是________。
15. 图1中的直角三角形有一条直角边长为3,将四个图1中的直角三角形分别拼成如图2,图3所示的正方形,其中阴影部分的面积分别记为S1,S2,则S1– S2的值为________。
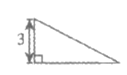

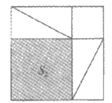
图1 图2 图3
16. 图1是一个2×2正方形网格,两条网格线的交点叫做格点。甲、乙两人在网格中进行游戏,规则如下:
图1 | 游戏规则 a. 两人依次在网格中画线段,线段的起点和终点均为格点; b. 新画线段的起点为前一条线段的终点,且与任意已画出线段不能有其他公共点; c. 已画出线段的所有端点中,任意三个端点不能在同一条直线上; d. 当某人无法画出新的线段时,则另一人获胜。 |
如图2,甲先画出线段AB,乙随后画出线段BC。若这局游戏继续进行下去,最终的获胜者是_________(填“甲“,“乙“或“不确定“)。
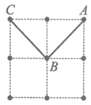
图2
三、解答题(本题共68分,第17-20题,每小题5分,第21题6分,第22题5分,第23题6分,第24题5分,第25-26题,每小题6分,第27-28题,每小题7分)
解答应写出文字说明、演算步骤或证明过程。
17. 计算:|-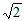 |-2cos45°+(π-1)0+
|-2cos45°+(π-1)0+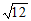 。
。
18. 解不等式组: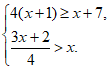
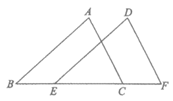
19. 如图,点B,E,C,F在一条直线上,AB∥DE,AB=DE,BE=CF。求证:∠A=∠D。
20. 已知a2+a-1=0,求代数式(a+2)(a-2)+a(a+2)的值。
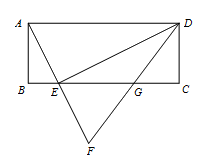
21. 如图,矩形ABCD中,点E在BC上,AE⊥ED。
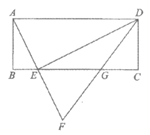
(1)求证:△ABE∽△ECD;
(2)F为AE延长线上一点,满足EF=AE,连接DF交BC于点G。
若AB=2,BE=1,求GC的长。
22. 我国是世界上最早发明历法的国家之一。《周礼》中记载:垒土为圭,立木为表,测日影,正地中,定四时。如图1,圭是地面上一根水平标尺,指向正北,表是一根垂直于地面的杆。正午,表的日影(即表影)落在圭上,根据表影的长度可以测定节气。
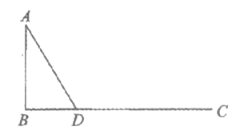
图1 图2
在一次数学活动课上,要制作一个圭表模型。如图2,地面上放置一根长2m的杆AB,向正北方向画一条射线BC,在BC上取点D,测得BD=1.5m,AD=2.5m。
(1)判断:这个模型中AB与BC是否垂直。答:________(填“是“或“否“);
你的理由是:_____________________________。
(2)某地部分节气正午时分太阳光线与地面夹角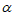 的值,如下表:
的值,如下表:
节气 | 夏至 | 秋分 | 冬至 |
太阳光线与地面夹角 | 74° | 50° | 27° |
①记夏至和冬至时表影分别为BM和BN,利用上表数据,在射线BC上标出点M和点N的位置;
②记秋分时的表影为BP,推测点P位于(
)
A. 线段MN中点左侧 B. 线段MN中点处 C. 线段MN中点右侧
23. 已知直线l:y=kx(k≠0)经过点A(-1,2)。点P为直线l上一点,其横坐标为m。过点P作y轴的垂线,与函数y=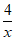 (x>0)的图象交于点Q。
(x>0)的图象交于点Q。
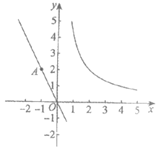
(1)求k的值;
(2)①求点Q的坐标(用含m的式子表示);
②若△POQ的面积大于3,直接写出点P的横坐标m的取值范围。
24. 牛年伊始,中国电影行业迎来了开门红。春节档期全国总观影人次超过1.6亿,总票房超过80亿元。以下是甲、乙两部春节档影片上映后的票房信息。
a. 两部影片上映第一周单日票房统计图
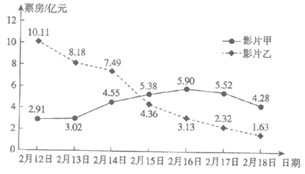
b. 两部影片分时段累计票房如下
上映影片 | 2月12日-18日累计票房(亿元) | 2月19日-21日累计票房(亿元) |
甲 | 31. 56 | |
乙 | 37. 22 | 2. 95 |
(以上数据来源于中国电影数据信息网)
根据以上信息,回答下列问题:
(1)2月12日-18日的一周时间内,影片乙单日票房的中位数为__________;
(2)对于甲、乙两部影片上映第一周的单日票房,下列说法中所有正确结论的序号是__________;
①甲的单日票房逐日增加;
②甲单日票房的方差小于乙单日票房的方差;
③在第一周的单日票房统计中,甲超过乙的差值于2月17日达到最大。
(3)截止到2月21日,影片甲上映后的总票房超过了影片乙,据此估计,2月19日-21日三天内影片甲的累计票房应超过__________亿元。
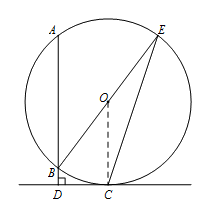
25. 如图,AB是⊙O的弦,C为⊙O上一点,过点C作AB的垂线与AB的延长线交于点D,连接BO并延长,与⊙O交于点E,连接EC,∠ABE=2∠E。
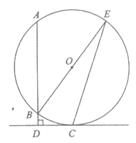
(1)求证:CD是⊙O的切线;
(2)若tanE=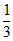 ,BD=1,求AB的长。
,BD=1,求AB的长。
26. 在平面直角坐标系xOy中,已知抛物线y=ax2-2ax+a-2(a>0)。分别过点M(t,0)和点N(t+2,0)作x轴的垂线,交抛物线于点A和点B。记抛物线在A,B之间的部分为图象G(包括A,B两点)。
(1)求抛物线的顶点坐标;
(2)记图象G上任意一点的纵坐标的最大值与最小值的差为m。
①当a=2时,若图象G为轴对称图形,求m的值;
②若存在实数t,使得m=2,直接写出a的取值范围。
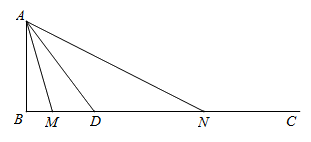
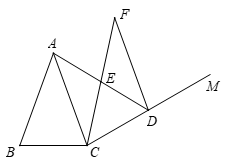
27. 如图,在△ABC中,AB=AC,∠BAC=40°,作射线CM,∠ACM=80°。D在射线CM上,连接AD,E是AD的中点,C关于点E的对称点为F,连接DF。
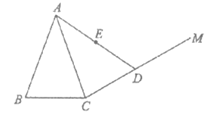
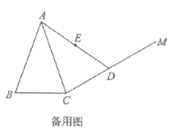
(1)依题意补全图形;
(2)判断AB与DF的数量关系并证明;
(3)平面内一点G,使得DG=DC,FG=FB,求∠CDG的值。
28. 在平面直角坐标系xOy中,对于点A和线段MN,如果点A,O,M,N按逆时针方向排列构成菱形AOMN,且∠AOM=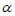 ,则称线段MN是点A的“
,则称线段MN是点A的“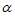 –相关线段“。例如,图1中线段MN是点A的“30°-相关线段“。
–相关线段“。例如,图1中线段MN是点A的“30°-相关线段“。
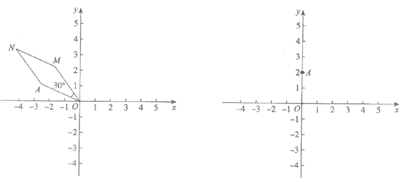
图1 图2
(1)已知点A的坐标是(0,2)。
①在图2中画出点A的“30°-相关线段“MN,并直接写出点M和点N的坐标;
②若点A的“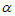 –相关线段“经过点(
–相关线段“经过点(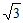 ,1),求
,1),求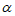 的值;
的值;
(2)若存在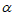 ,
,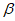 (
(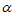 ≠
≠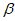 )使得点P的“
)使得点P的“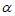 –相关线段“和“
–相关线段“和“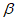 –相关线段“都经过点(0,4),记PO=t,直接写出t的取值范围。
–相关线段“都经过点(0,4),记PO=t,直接写出t的取值范围。
参考答案
一、选择题
(本题共16分,每小题2分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | A | C | A | B | D | C | A | D |
二、填空题(本题共16分,每小题2分)
9. 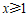 10.
10.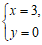
11. 110° 12. 答案不唯一,如: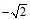
13. 1 14. 2或-6
15. 9 16. 乙
三、解答题(本题共68分,第17-20题,每小题5分,第21题6分,第22题5分,第23题6分,第24题5分,第25–26题,每小题6分,第27–28题,每小题7分)
解答应写出文字说明、演算步骤或证明过程.
17. (本小题满分5分)
解:原式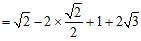
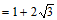 .
.
18. (本小题满分5分)
解:原不等式组为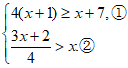
解不等式①,得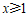 .
.
解不等式②,得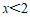 .
.
∴
原不等式组的解集为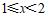 .
.
19. (本小题满分5分)
证明:∵
AB∥DE,
∴
∠B=∠DEF.
∵
BE=CF,
∴
BE+EC=CF+EC.
∴
BC=EF.
在△ABC和△DEF中,
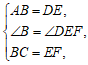
∴ △ABC ≌ △DEF.
∴
∠A=∠D.
20. (本小题满分5分)
解: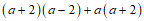
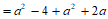
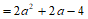
∵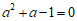
∴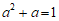
∴
原式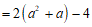
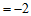
21. (本小题满分6分)
(1)证明:∵
四边形ABCD是矩形,
∴
∠B=∠C=90°.
∴
∠BAE+∠AEB=90°.
∵
AE⊥ED,
∴
∠AED=90°.
∴
∠AEB+∠CED=90°.
∴
∠BAE=∠CED.
∴ △ABE
∽ △ECD.
(2)解:∵
由(1),△ABE
∽ △ECD,
∴
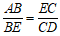 .
.
∵
矩形ABCD中,CD=AB=2,BE=1,
∴
EC=4.
∴
BC=BE+EC=5.
∵
AD∥BC,
∴ △AFD
∽ △EFG.
∴
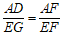 .
.
∵
AE=EF,
∴
AF=2EF.
∴
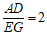 ,即
,即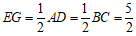 .
.
∴
CG=EC–EG= .
.
22. (本小题满分5分)
(1)是,
理由:由测量结果可知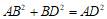 ,由勾股定理的逆定理可知AB⊥BC.
,由勾股定理的逆定理可知AB⊥BC.
(2)①
如图,点M和点N即为所求.
② A.
23. (本小题满分6分)
(1)解:∵
直线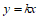 过点A(
过点A(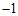 ,2),
,2),
∴
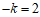 ,即
,即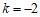 .
.
(2)①
解:∵ P在直线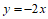 上且横坐标为m,
上且横坐标为m,
∴
点P的纵坐标为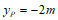 ,
,
∵
PQ⊥y轴,
∴
点Q的纵坐标为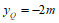 .
.
∵
点Q在函数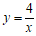 (
(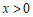 )的图象上,
)的图象上,
∴
点Q的横坐标为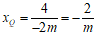 .
.
∴
点Q的坐标为(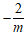 ,
,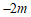 ).
).
②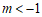
24. (本小题满分5分)
(1)4.36
(2)②③
(3)8.61
25. (本小题满分6分)
(1)证明:连接OC,在⊙O中
∵
∠BOC=2∠E,∠ABE=2∠E,
∴
∠BOC=∠ABE.
∴
AB∥OC.
∴
∠OCD+∠ADC=180°.
∵
AB⊥CD于点D,
∴
∠ADC=90°.
∴
∠OCD=90°.
∴
OC⊥CD.
∴
CD是⊙O的切线.
(2)解:方法1:
连接AC,BC,
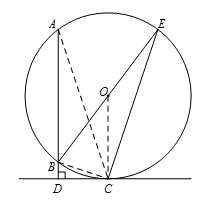
∵
BE是⊙O的直径,
∴
∠BCE=90°.
∴
∠OBC+∠E=90°.
∵
∠OCD=90°,
∴
∠OCB+∠BCD=90°.
∵
OB=OC,
∴
∠OCB=∠OBC.
∴
∠E=∠BCD.
∴
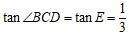 .
.
∴
在Rt△BCD中,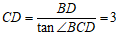 .
.
∵
∠A=∠E,
∴
在Rt△ACD中,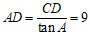 .
.
∴
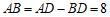 .
.
方法2:
连接CD,过点O作OH⊥AB于H,设⊙O的半径为r.
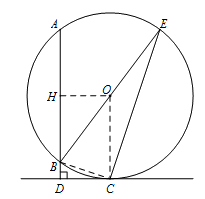
同方法1可得∠BCD=∠E,CD=3.
∵
OH⊥AB,
∴
∠OHD=90°=∠OCD=∠ADC.
∴
四边形OHDC是矩形.
∴
OH=CD=3,HD=OC=r,
∴
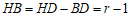 .
.
∵ Rt△OHB中,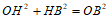 ,
,
∴
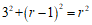 .
.
解得: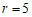 .
.
∴
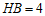 .
.
∴
由垂径定理,AB=2HB=8.
26. (本小题满分6分)
解:(1)抛物线的解析式为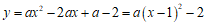 ,
,
∴
抛物线的顶点坐标为(1,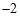 ).
).
(2)①
当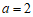 时,抛物线为
时,抛物线为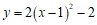 ,其对称轴为
,其对称轴为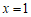 .
.
∵
图象G为轴对称图形,
∴
点A,B必关于对称轴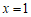 对称.
对称.
∵
点A的横坐标为t,点B的横坐标为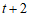 ,
,
∴
AB=2,
∴
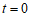 ,点A为(0,0),点B为(2,0).
,点A为(0,0),点B为(2,0).
∵
当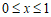 时,y随x的增大而减小,当
时,y随x的增大而减小,当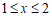 时,y随x的增大而增大,
时,y随x的增大而增大,
∴
图象G上任意一点的纵坐标最大值为0,最小值为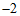 .
.
∴
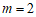 .
.
②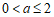
27. (本小题满分7分)
解:(1)下图即为所求
(2)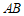 与
与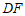 的数量关系是AB=DF.
的数量关系是AB=DF.
证明:∵
点F与点C关于点E对称,
∴
CE=FE.
∵
E是AD的中点,
∴
AE=DE.
∵
∠AEC=∠DEF,
∴ △AEC
≌ △DEF
∴
AC=DF.
∵
AB=AC,
∴
AB=DF.
(3)如图所示,点G的位置有两种情况.
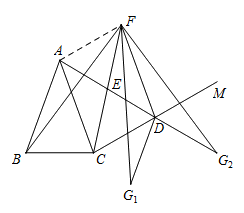
①
点G与点C在直线DF同侧时,记为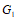 ,连接AF,
,连接AF,
∵
AE=DE,CE=EF,
∴
四边形ACDF是平行四边形.
∴
AF=CD.
∵
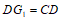 ,
,
∴
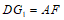 ,
,
∵
AB=DF,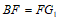 ,
,
∴ △ABF
≌ △DF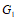 .
.
∴
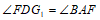 .
.
∵
□ACDF中,∠CAF=∠CDF,
∴
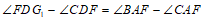 .
.
∴
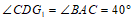 .
.
②
点G与点C在直线DF异侧时,记为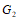 ,
,
∵
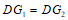 ,
,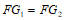 ,DF=DF,
,DF=DF,
∴ △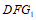
≌ △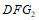 .
.
∴
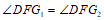 .
.
∵
□ACDF中,AC∥DF,∠ACD=80°,
∴
∠CDF=180°-∠ACD=100°.
∵
由①,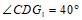 ,
,
∴
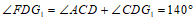 .
.
∴
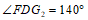 .
.
∴
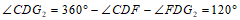 .
.
综上,∠CDG的度数为40°或120°
28. (本小题满分7分)
(1)①
如图,MN即为所求.
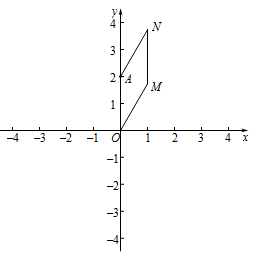
点M的坐标是(1,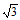 ),点N的坐标是(1,
),点N的坐标是(1,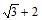 ).
).
②
解:
∵
点A的“α–相关线段“MN经过点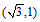 ,
,
∴
点M必在直线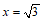 上.
上.
记直线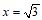 与x轴交于点H(
与x轴交于点H(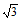 ,0),
,0),
∵
OM=OA=2,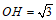 ,
,
∴
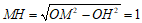 ,
,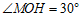 .
.
分两种情况:
a) 当点M在x轴上方时,点M恰为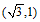 ,符合题意,
,符合题意,
此时∠AOM=60°,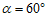 ;
;
b) 当点M在x轴下方时,点M恰为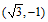 ,由MN=2知点N为
,由MN=2知点N为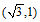 ,
,
也符合题意,此时∠AOM=120°,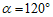 .
.
综上,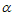 的值为60°或120°.
的值为60°或120°.
(2)