考试时长 90分钟,满分100分。
第一部分:学考数学(共70分)
一、选择题:本大题共8题,每小题4分,共32分
1. 已知数列{an}的前n项和Sn=n2-1,那么a3等于( )
A. 5 B. 6 C. 7 D. 8
2. 已知数列{an}中,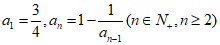 ,那么a2021等于( )
,那么a2021等于( )
A. 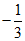 B.
B. 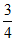 C. 2 D. 4
C. 2 D. 4
3. 已知数列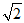 ,
,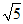 ,
, 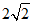 ,
,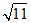 ,…,则
,…,则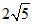 是这个数列的( )
是这个数列的( )
A. 第六项 B. 第七项 C. 第八项 D. 第九项
4. 设等差数列{an}的前n项和为Sn,若a1=-11,a4+a6=-6,则当Sn取最小值时,n等于( )
A. 6 B. 7 C. 8 D. 9
5. 等比数列{an}中,a1+a2+a3=30,a4+a5+a6=120,则a7+a8+a9=( )
A. 240 B. ±240 C. 480 D. ±480
6. 若b为a,c的等比中项,则函数y=ax2+bx+c的图象与x轴的交点个数为( )
A. 0 B. 1 C. 2 D. 不能确定
7. 数列0.3,0.33,0.333,0.3333,…的通项公式是an=( )
A. 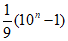 B.
B. 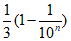 C.
C. 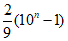 D.
D.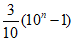
8. 为改善环境,某城市对污水处理系统进行改造,三年后,城市污水排放量由原来每年排放125万吨降到27万吨,那么污水排放量平均每年降低的百分率是( )
A. 60% B. 50% C. 40% D. 30%
二、填空题:本大题共4小题,每小题4分,共16分.
9. 在数列{an}中,a1=2,an+1=2an,Sn为{an}的前n项和. 若Sn=126,则n=__________.
10. 已知{an}是等差数列,a2+a4+a6+a8=16,则S9=__________.
11. 已知数列{an}是递增的等比数列,a1+a4=9,a2a3=8,则数列{an}的前n项和等于__________.
12. 在等差数列{an}中,a1=3,a4=2,则a1+a4+a7+…+a3n+1=_________·
三、解答题:共3道大题,共22分,请写出解题步骤.
13. (6分)设数列{an}是等比数列,其前n项和为Sn,且S3=3a3,求此数列的公比q.
14. (8分)已知数列{an}满足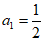 且
且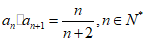 .
.
(1)求a2,a3,a4,并猜想数列{an}的通项公式. (4分)
(2)用数学归纳法证明你的猜想. (4分)
15. (8分)已知数列{an}是公差不为0的等差数列,a1=1,且a1,a3,a9成等比数列.
(1)求数列{an}的通项公式. (4分)
(2)设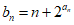 ,求数列{bn}的前n项和Sn
,求数列{bn}的前n项和Sn
(4分)
第二部分:SAT数学(10道小题,每小题3分,共30分)
1. x+y=75
The equation above relates the number of minutes, x, Maria spends running each day and the number of minutes, y, she spends biking each day. In the equation, what does the number 75 represent?
A)The number of minutes spent running each day
B)The number of minutes spent biking each day
C)The total number of minutes spent running and biking each day
D)The number of minutes spent biking for each minute spent running
2. Which of the following is equivalent to 3(x+5) -6?
A) 3x-3
B) 3x-1
C) 3x+9
D) 15x-6
3. x=y-3
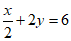
Which ordered pair (x, y) satisfies the system of equations shown above?
A)(-3,0)
B)(0,3)
C)(6,-3)
D) (36,-6)
4. Which of the following complex numbers is equal to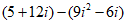 ,for
,for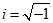 ?
?
A)-14-18i
B)-4-6i
C)4+6i
D)14+18i
5. If 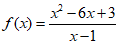 ,what is
,what is 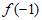 ?
?
A)-5
B)-2
C)2
D)5
6. In the equation (ax+3)2=36, a is a constant. If x=-3 is one solution to the equation, what is a possible value of a?
A)-11
B)-5
C)-1
D)0
7. Questions 7 and 8 refer to the following information.
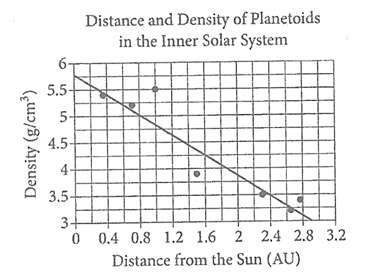
The scatterplot above shows the densities of 7 planetoids, in grams per cubic centimeter, with respect to their average distances from the Sun in astronomical units (AU). The line of best fit is also shown.
7. According to the scatterplot, which of the following statements is true about the relationship between a planetoid’s average distance from the Sun and its density?
A) Planetoids that are more distant from the Sun tend to have lesser densities.
B) Planetoids that are more distant from the Sun tend to have greater densities.
C) The density of a planetoid that is twice as far from the Sun as another planetoid is half the density of that other planetoid.
D) The distance from a planetoid to the Sun is unrelated to its density.
8. An astronomer has discovered a new planetoid about 1.2 AU from the Sun. According to the line of best fit, which of the following best approximates the density of the planetoid, in grams per cubic centimeter?
A) 3.6
B) 4.1
C) 4.6
D) 5.5
9. 9ax+9b-6=21
Based on the equation above, what is the value of ax+b?
A) 3
B) 6
C) 8
D) 12
10. Lani spent 15% of her 8-hour workday in meetings. How many minutes of her workday did she spend in meetings?
A) 1.2
B) 15
C) 48
D) 72
参考答案
第一部分:学考数学(共70分)
一、选择题:本大题共8小题,每小题4分,共32分。
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | A | A | B | A | C | A | B | C |
二、填空题:本大题共4小题,每小题4分,共16分。
9. 6 ; 10. 36
11. 2n-1; 12.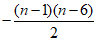
三、解答题:共3道大题,共22分,请写出解题步骤。
13. 若q=1,则S3=a1+a2+a3=3a3,符合要求; …………2分
若q≠1,则
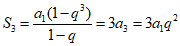 , …………2分
, …………2分
(或者,S3=a1+a1q+a1q2=3a3=3a1q2)
化简得2q2-q-1=0,解得
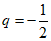 …………2分
…………2分
所以q=1或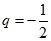
14. ∵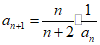 ,
,
∴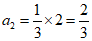 ,
,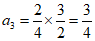 ,
,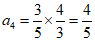 …………3分
…………3分
猜想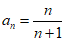 . ………1分
. ………1分
(2)用数学归纳法证明你的猜想. (4分)
证明:当n=1时,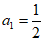 ,等式显然成立,
,等式显然成立,
…………1分
假设当n=k时,等式成立,即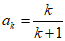 ,
,
……1分
则当n=k+1时,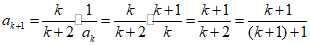 ,
,
即当n=k+1时,等式成立, …………2分
故对任意n∈N*,有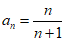 .
.
15. (1)
公差d≠0
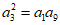
(1+2d)2=1+8d 2分
d=1………………1分
an=n……………………1分
(2)
Sn=(1+2+…+n)+(21+22+…2n) ………………2分
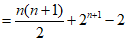 ………………2分
………………2分
第二部分:SAT数学(共30分)
(选择题,共10小题,每小题3分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | C | C | B | D | A | C | B | C | B | B |
