本试卷有三道大题,考试时长100分钟,满分100分。
一、选择题(本大题共10小题,共30分)
1.16的算术平方根是( )
A.4 B.-4 C.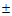 4 D.±8
4 D.±8
2.课间操时,小华、小军和小刚的位置如图所示,如果小华的位置用(0,0)表示,小军的位置用(2,1)表示,那么小刚的位置可以表示为( )
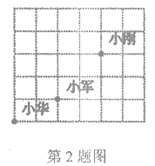
A.(5,4) B.(4,5) C.(3,4) D.(4,3)
3.将某图形的各点的横坐标减去2,纵坐标保持不变,可将该图形( )
A.横向向右平移2个单位 B.横向向左平移2个单位
C.纵向向上平移2个单位 D.纵向向下平移2个单位
4.不等式x+1≥2的解集在数轴上表示正确的是( )
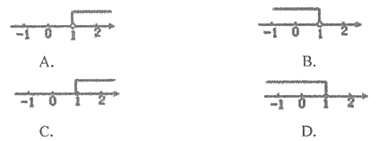
5.如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=100°,则∠4的度数是( )
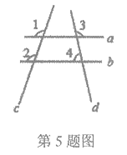
A.70° B.80° C.100° D.110°
6.若a>b,则下列各式中一定成立的是( )
A.a-2<b-2 B.ac2>bc2
C.-2a>-2b D.a+2>b+2
7.下列说法:①相等的角是对顶角;②同位角相等;
③过一点有且只有一条直线与已知直线平行;
④直线外一点到这条直线的垂线段的长度,叫做点到直线的距离
其中真命题有( )个.
A.1 B.2
C.3 D.4
8.若点P(1+a,1-b)在第二象限,则点Q(a,b-1)在第( )象限.
A.一 B.二
C.三 D.四
9.已知min{a,b,c}表示取三个数中最小的那个数,例如:当x=-2时,min{|x|,x2,x3}=min{|-2|,(-2)2,(-2)3}=-8当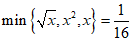 时,则x的值为( )
时,则x的值为( )
A.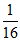 B.
B.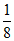
C.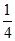 D.
D.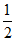
10.数学中有许多形状优美、寓意美好的曲线,曲线C就是其中之一(如图).给出下列三个结论:
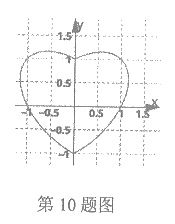
①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);
②曲线C在第一、二象限中的任意一点到原点的距离大于1:
③曲线C所围成的“心形“区域的面积小于3.
其中正确结论的序号是( )
A.① B.②
C.①② D.①②③
二、填空题(本大题共10小题,共20分)
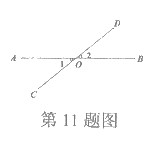
11.如图所示,直线AB,CD交于O,∠1=20°,则∠2=________,理由是_____________.
12.在-0.4,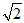 ,4,
,4,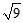 ,
,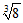 ,-π,
,-π,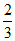 中,无理数有_______个.
中,无理数有_______个.
13.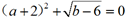 ,则(a,b)在第____象限.
,则(a,b)在第____象限.
14.直线AB、CD交于O,∠AOC:∠BOC=2:1,OA⊥OE,则∠EOD=_______.
15.比较大小: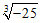 _____-3,
_____-3,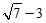 _____
_____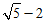 (填“<“或“>”).
(填“<“或“>”).
16.将点P(-2,3)先向右平移2个单位,再向上平移3个单位后,则平移后点P的坐标是________.
17.已知,点A(3,0),点B在y轴上,S△ABO=6,则B点坐标为______________.
18.已知5x+19的立方根是4,则2x+7的平方根为______________.
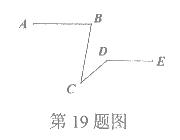
19.如图,已知AB∥DE,∠ABC=80°,∠CDE=140°,则∠BCD=_______°.
20.我们可以从解方程的角度理解从有理数扩充到实数的必要性.若a(a≥0)不是某个有理数的平方,则方程x2=a在有理数范围内无解;若b不是某个有理数的立方,则方程x3=b在有理数范围内无解,而在实数范围内以上方程均有解,这是扩充数的范围的一个好处。根据你对实数的理解,选出正确命题的序号______________.
①x9=3在实数范围内有解;②x2020-5=0在实数范围内的解不止一个;
③x2+x4=5在实数范围内有解,解介于1和2之间;
④对于任意的a(a≥0),恒有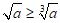 .
.
三、解答题(本大题共10小题,共50分)
21.(共4分)如图,P是∠ABC内一点,按要求完成下列问题:
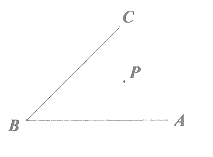
(1)过点P作AB的垂线,垂足为点D;
(2)过点P作BC的平行线,交AB于点E;
(3)比较线段PD和PE的大小,并说明理由.
22.(每小题3分,共6分)计算题.
(1)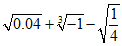
(2)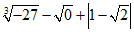
23.(每小题3分,共6分)求下列各式中x的值.
(1) 2x3=16 (2)(x-l)2=64
24.(每小题3分,共6分)解下列不等式,并把解集表示在数轴上.
(1)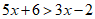
(2)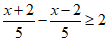
25.(共4分)已知:如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠3.那么AD是∠BAC的平分线吗?若是,请说明理由,请完成下列证明并在下面的括号内填注依据.
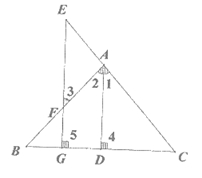
解:是,理由如下:
∵AD⊥BC,EG⊥BC(已知),
∴∠4=∠5=90°(垂直定义),
∴AD∥EG (____________________);
∴∠1=∠E (两直线平行,同位角相等);
∠2=_______(________________________);
∵∠E=∠3(已知),
∴∠1=∠2(等量代换);
∴AD平分∠BAC (________________________).
26.(共4分)如图,这是某市部分建筑分布简图,若火车站的坐标为(-1,2),市场的坐标为(3,5),请在图中画出平面直角坐标系,并分别写出超市、体育场和医院的坐标.
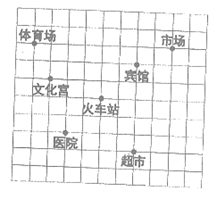
超市的坐标为________________;体育场的坐标为________________;医院的坐标为________________.
27.(共4分)已知关于x的方程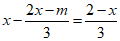 的解是非负数,求m的取值范围.
的解是非负数,求m的取值范围.
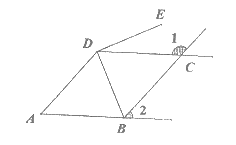
28.(共5分)已知:如图,DB平分∠ADC,∠1+∠2=180°.
(1)求证:AB∥CD;
(2)若ED⊥DB,∠A=50°,求∠EDC的大小
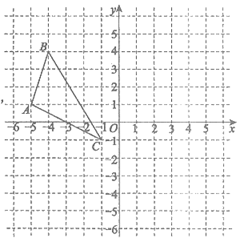
29.(共5分)如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(-5,1),B(-4,4),C(-1,-1).将△ABC进行平移,使点A移动到点A’(0,2),得到△A’B’C’,其中点A’,B’,C’分别为点A,B,C的对应点.
(1)请在所给坐标系中画出△A’B’C’,并直接写出点C’的坐标;
(2)求△ABC的面积;
(3)直线l过点(0,-3)且平行于x轴,在直线l上求一点Q使△ABC与△ABQ的面积相等,请写出点Q的坐标
解:(1)点C’的坐标为________;
(2)△ABC的面积为________;
(3)Q点的坐标为________.
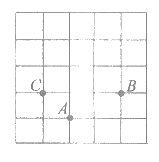
30.(共6分)已知整点P0在平面直角坐标系内做“跳马运动“(也就是中国象棋式“日字“型跳跃)。例如,在下图中,从点A做一次“跳马运动“可以到点B,但是到不了点C.
设P0做一次跳马运动到点P1,再做一次跳马运动到点P2,再做一次跳马运动到点P3,……,如此继续下去.
(1)若P0(1,0),则P1可能是下列哪些点________;D (-1,2) E(-1, -1) F(-2,0)
(2)已知点P0(9,3),P2(5,3),则点P1的坐标为________________;
(3)P0为平面上一个定点,则点P7、P26可能与P0重合的是____________________;
(4) P0为平面上一个定点,则线段P0P7长的最小值是____________________;
(5)现在P0(1,0),规定每一次只向x轴的正方向跳跃,若P21(38,10),则P1,P2,...,P20点的纵坐标的最大值为____________.
参考答案
一、选择题(本大题共10小题,共30分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | A | D | B | C | B | D | A | C | C | C |
二、填空题(本大题共10小题,共20分)
11.20°,对顶角相等 12.2 13.二 14.30°或150° 15.>,<
16.(0,6) 17.(0,4)或(0,-4) 18.±5 19.40° 20.①②
三、解答题(本大题共10小题,共50分)
21.(4分)(1)(2)略,(3)PD<PE,理由:垂线段最短
22.(6分)(1) -1.3 (2)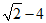
23.(6分)(1)x=2 (2)x=9或x=-7
24.(6分)(1) x>-4 (2) x≤-2 数轴表示略
25.(4分)同位角相等,两直线平行;∠3;两直线平行,内错角相等;角平分线定义
26.(4分)图略,超市(1,-1),体育场(-5,5),医院(-3,0)
27.(4分)m≤2
28.(5分)(1)略 (2) 25°
29.(5分)(1)(4,0)(2)7 (3)(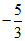 ,-3)或(-11,-3)
,-3)或(-11,-3)
30.(6分)(1)E(2)(7,2)或(7,4)
(3) P26
(4)1 (5) 18
