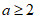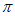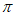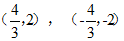(本试卷满分100分,考试时间120分钟)
一、选择题(本题共16分,每小题2分)
1. 下面的几何体中,俯视图为三角形的是(
)

A B C D
2. 为解决延期开学期间全市初高三学生的学习需求,提升学生的实际获得,北京市教委打造了“答疑平台“,全市144000名初高三学生全部纳入在线答疑辅导范围。将144000用科学记数法表示应为(
)
A. 144×103 B. 14.4×104 C. 1.44×105 D. 1.44×106
3. 如图,直线a与直线b平行,将三角板的直角顶点放在直线a上,若∠1=40゜,则∠2等于(
)
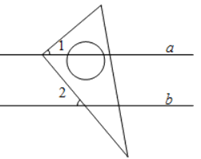
A. 40゜ B. 50゜ C. 60゜ D. 140゜
4. 一个多边形的内角和是外角和的2倍,则这个多边形的边数为(
)
A. 5 B. 6 C. 7 D. 8
5. 实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是(
)
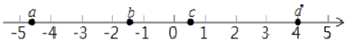
A. a>-4 B. bd>0 C. |a|>|b| D. b+c>0
6. 把2a2-8分解因式,结果正确的是(
)
A. 2(a2-4) B. 2(a-2)2 C. 2(a+2)(a-2) D. 2(a+2)2
7. 如图,在△ABC中,∠ABC=90゜,点D、E、F分别是边AB、BC、CA的中点,若DE+BF=8,则BF的值为(
)
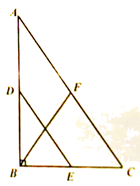
A. 3 B. 4 C. 5 D. 6
8. 一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
A类 | 50 | 25 |
B类 | 200 | 20 |
C类 | 400 | 15 |
例如,购买A类会员卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数介于45~55次之间,则最省钱的方式为(
)
A. 购买A类会员年卡 B. 购买B类会员年卡
C. 购买C类会员年卡 D. 不购买会员年卡
二、填空题(本题共16分,每小题2分)
9. 如果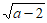 在实数范围内有意义,那么实数a的取值范围是__________。
在实数范围内有意义,那么实数a的取值范围是__________。
10. 写出一个比3大且比4小的无理数:_________。
11. 掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,掷得面朝上的点数为奇数的概率为_________。
12. 如果a+b=2,那么代数式(a-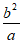 )·
)·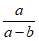 的值是_________。
的值是_________。
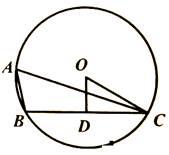
13. 如图,⊙O的半径为4,点A为⊙O上一点,OD⊥弦BC于点D,OD=2,则∠BAC=__________。
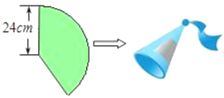
14. 小刚用一张半径为24cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为10cm,那么这张扇形纸板的面积是__________cm2。
15. 在平面直角坐标系中,将△AOB以点O为位似中心,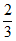 为位似比作位似变换,得到△A1OB1,已知A(2,3),则点A1的坐标是___________。
为位似比作位似变换,得到△A1OB1,已知A(2,3),则点A1的坐标是___________。
16. 在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y’),给出如下定义:
若y’=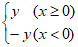 ,则称点Q为点P的“可控变点“。
,则称点Q为点P的“可控变点“。
(1)点(-3,4)的“可控变点“的坐标为___________;
(2)若点N(m,2)是函数y=x-1图象上点M的“可控变点“,则点M的坐标为___________。
三、解答题(本题共68分,第17~20题每小题5分,第21题6分,第22题5分,第23~24题每小题6分,第25题5分,第26题6分,第27~28题每小题7分)
17. 计算:4cos30゜+(1-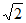 )0–
)0–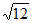 +|-2|。
+|-2|。
18. 解不等式组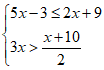 。
。
19. 已知x2+4x+3=0,求代数式(x+3)2-2(x-2)的值。
20. 关于x的一元二次方程x2–(k+3)x+2k+2=0。
(1)求证:方程总有两个实数根;
(2)若方程有一根小于1,求k的取值范围。
21. 甲、乙两列高铁列车在不同的时刻分别从北京出发开往上海。已知北京到上海的距离约为1320千米,列车甲行驶的平均速度为列车乙行驶平均速度的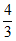 倍,全程运行时间比列车乙少1.5小时,求列车甲从北京到上海运行的时间。
倍,全程运行时间比列车乙少1.5小时,求列车甲从北京到上海运行的时间。
22. 如图,在□ABCD中,∠BAD的平分线交CD于点E,交BC的延长线于点F,连接BE,∠F=45゜。
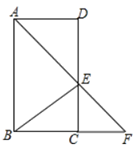
(1)求证:四边形ABCD是矩形;
(2)若AB=14,DE=8,求sin∠ABE的值。
23. 已知:在平面直角坐标系xOy中,对于任意的实数a(a≠0),直线y=ax+a-2都经过平面内一个定点A。
(1)求点A的坐标;
(2)反比例函数y=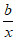 的图象与直线y=ax+a-2交于点A和另外一点P(m,n)。
的图象与直线y=ax+a-2交于点A和另外一点P(m,n)。
①求b的值;
②当n>-2时,求m的取值范围。
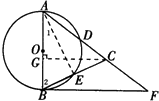
24. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=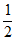 ∠CAB。
∠CAB。
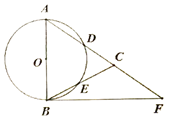
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=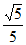 ,求BC和BF的长。
,求BC和BF的长。
25. 在电影《流浪地球》和《绿皮书》上映期间,为了解某大学1800名学生对两部电影的喜爱程度,调查小组随机抽取了该大学20名学生对两部电影的打分,过程如下。
收集数据 20名大学生对两部电影的打分结果如下:
《流浪地球》
78 | 75 | 99 | 98 | 79 | 67 | 88 | 78 | 76 | 98 |
88 | 79 | 97 | 91 | 78 | 80 | 93 | 90 | 99 | 99 |
《绿皮书》
88 | 79 | 68 | 97 | 85 | 74 | 96 | 84 | 92 | 97 |
89 | 81 | 91 | 75 | 80 | 85 | 91 | 89 | 97 | 92 |
(1)整理、描述数据
绘制了如下频数分布直方图和统计表,请补充完整;
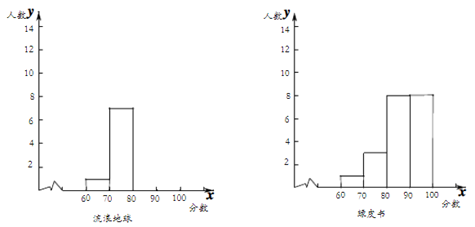
(说明:60≤x<70表示一般喜欢,70≤x<80表示比较喜欢,80≤x<0表示喜欢,90≤x<100表示超级喜欢)
电影 | 平均数 | 众数 | 中位数 |
《流浪地球》 | 86. 5 | 99 | |
《绿皮书》 | 86. 5 | 88. 5 |
分析数据、推断结论
(2)估计该大学超级喜欢电影《绿皮书》的有___________人;
(3)你认为观众更喜欢这两部电影中的___________(填《流浪地球》或《绿皮书》),理由是____________________________________________。
26. 已知抛物线G:y=mx2-2mx-3有最低点。
(1)求二次函数y=mx2-2mx-3的最小值(用含m的式子表示);
(2)将抛物线G向右平移m个单位得到抛物线G1。经过探究发现,随着m的变化,抛物线G1顶点的纵坐标y与横坐标x之间存在一个函数关系,求这个函数关系式,并写出自变量x的取值范围;
(3)记(2)所求的函数为H,抛物线G与函数H的图象交于点P(s,t),直接写出点P的纵坐标t的取值范围。
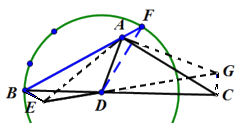
27. 如图,△ABC中,AB=AC=2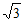 ,∠BAC=120゜,点D为BC边上任意一点,将DA绕D点逆时针旋转120゜得到DE。连接AE,将AE绕A点逆时针旋转120゜得到AG,连接CG。
,∠BAC=120゜,点D为BC边上任意一点,将DA绕D点逆时针旋转120゜得到DE。连接AE,将AE绕A点逆时针旋转120゜得到AG,连接CG。
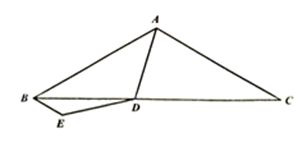
(1)依题意补全图形;
(2)求∠EBD的度数;
(3)直接写出BE2,CD2与AD2的数量关系。
28. 对于平面直角坐标系xOy中的图形G和图形W:若在图形G上存在点P,使得P到图形W上各点的最短距离为1,称图形G为图形W的同类图形,点P为图形W的同类点。
(1)已知直线l:y=x,
①判断直线m:y=-x是否为直线l的同类图形。如果是,写出直线l的同类点P的坐标,如果不是,请说明理由;
②点A为x轴上一动点,⊙A半径为1,若⊙A为直线l的同类图形,求点A的横坐标xA的取值范围;
(2)已知坐标轴上的点R(5,0),Q(0,5)。点B,C在直线y=x+b上,且B(-1,t),C(1,s)。线段RQ是线段BC的同类图形,直接写出b的取值范围。
参考答案
一、选择题(本题共16分,每小题2分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | D | C | B | B | C | C | B | C |
二、填空题(本题共16分,每小题2分)
题号 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
答案 |
|
| 0.5 | 2 | 60 | 240 |
| (-3,-4) | (3,2), (-1,-2) |
三、解答题(本题共68分,第17~20题每小题5分,第21题6分,第22题5分,第23~24题每小题6分,第25题5分,第26题6分,第27~28题每小题7分)
17. 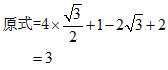 ——————4
——————4
—————— 5
18. 由(1)得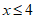 ——————————2
——————————2
由(2)得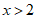 ——————————4
——————————4
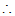 不等式组的解集为
不等式组的解集为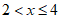 ————————5
————————5
19. 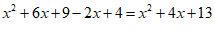 ——————3
——————3
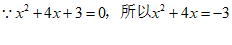 —————4
—————4
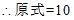 ——————5
——————5
20.(1)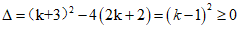
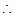 方程总有两个实数根 ——————2
方程总有两个实数根 ——————2
(2)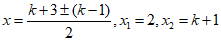
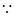 有一个根小于1,
有一个根小于1,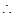
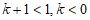 ——————5
——————5
21. 解:设列车甲从北京到上海的运行速度为每小时x 千米 ————1
则
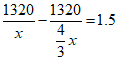
解得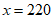 ——————3
——————3
经检验,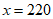 为原方程的解且符合题意 ——————4
为原方程的解且符合题意 ——————4
时间: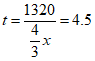 ——————5
——————5
答:列车甲从北京到上海运行的时间为4.5小时 ——————6
22. (1)证明: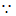 四边形
四边形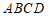 是平行四边形,
是平行四边形,
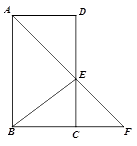
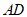 //BC.
//BC.
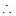 ∠DAF=∠F.
∠DAF=∠F.
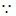 ∠F=45°,
∠F=45°,
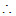 ∠DAE=45°.………………………………………1分
∠DAE=45°.………………………………………1分
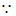 AF是∠BAD的平分线,
AF是∠BAD的平分线,
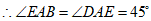 .
.
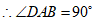 .
.
又 四边形
四边形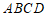 是平行四边形,
是平行四边形,
 四边形ABCD是矩形. …………………………2分
四边形ABCD是矩形. …………………………2分
(2)解:过点B作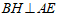 于点H,如图.
于点H,如图.
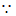 四边形ABCD是矩形,
四边形ABCD是矩形,
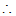 AB=CD,AD=BC,∠DCB=∠D=90°.
AB=CD,AD=BC,∠DCB=∠D=90°.
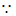 AB=14,DE=8,
AB=14,DE=8,
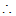 CE=6.
CE=6.
在Rt△ADE中,∠DAE=45°,
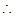 ∠DEA=∠DAE=45°.
∠DEA=∠DAE=45°.
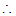 AD=
AD=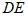 =8.
=8.
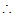 BC=8.
BC=8.
在Rt△BCE中,由勾股定理得
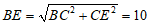 . ……………………………………………3分
. ……………………………………………3分
在Rt△AHB中,∠HAB=45°,
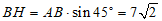 . …………………………………………4分
. …………………………………………4分
 在Rt△BHE中,∠BHE=90°,
在Rt△BHE中,∠BHE=90°,
 sin∠AEB=
sin∠AEB=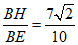 . ……………………………………………5分
. ……………………………………………5分
23.(1)解:(1)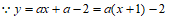 ,
,
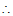 当
当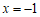 时,
时,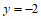 ,
,
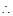 直线
直线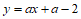 都经过平面内一个定点
都经过平面内一个定点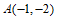 ;——————3
;——————3
(2)①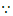 反比例函数
反比例函数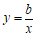 的图象经过点
的图象经过点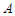 ,
,
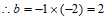 ;
;
②若点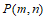 在第一象限,当
在第一象限,当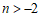 时,
时,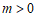 ,
,
若点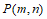 在第三象限,当
在第三象限,当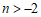 时,
时,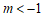 ,
,
综上,当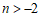 时,
时,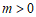 或
或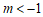 . ————————6
. ————————6
24. 解:(1)证明:连接AE,
∵AB是⊙O的直径,∴∠AEB=90°,∴∠1+∠2=90°.
∵AB=AC,∴∠1=∠CAB.
∵∠CBF=∠CAB,∴∠1=∠CBF ∴∠CBF+∠2=90°
即∠ABF=90°
∵AB是⊙O的直径,∴直线BF是⊙O的切线. ——————3
(2)过点C作CG⊥AB于点G.
∵sin∠CBF=,∠1=∠CBF,∴sin∠1=
∵∠AEB=90°,AB=5,∴BE=AB•sin∠1=,
∵AB=AC,∠AEB=90°,∴BC=2BE=2,
在Rt△ABE中,由勾股定理得AE=2,
∴sin∠2=,cos∠2=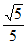 ,
,
在Rt△CBG中,可求得GC=4,GB=2,∴AG=3,
∵GC∥BF,∴△AGC∽△BFA ∴
∴BF== ————————6
25.(1)
补图 ————1
88 ,97 ————3
(2)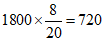 ,由此可以估计超级喜欢《绿皮书》的约有720人 ————5
,由此可以估计超级喜欢《绿皮书》的约有720人 ————5
(3)答案不唯一:
如:观众更喜欢这两部电影中的《绿皮书》
理由是喜欢《绿皮书》的中位数高于喜欢《流浪地球》的中位数 ——————5
26. 解:(1)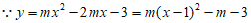 ,抛物线有最低点,
,抛物线有最低点,
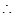 二次函数
二次函数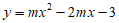 的最小值为
的最小值为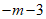 ;——————1
;——————1
(2)∵抛物线G: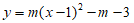
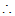 平移后的抛物线
平移后的抛物线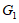 :
: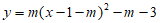
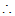 抛物线
抛物线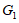 顶点坐标为
顶点坐标为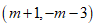
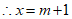 ,
,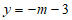
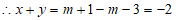
即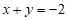 ,变形得
,变形得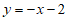
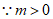 ,
,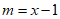
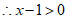
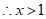
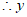 与x的函数关系式为
与x的函数关系式为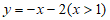 ;————4
;————4
(3)法一:如图,函数H: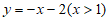 图象为射线
图象为射线
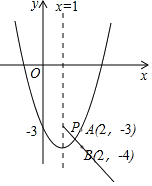
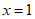 时,
时,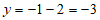 ;
;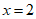 时,
时,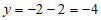
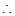 函数H的图象恒过点
函数H的图象恒过点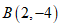
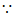 抛物线G:
抛物线G: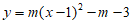
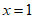 时,
时,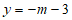 ;
;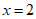 时,
时,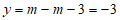
 抛物线G恒过点
抛物线G恒过点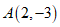
由图象可知,若抛物线与函数H的图象有交点P,则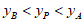 ,
,
 点P纵坐标的取值范围为
点P纵坐标的取值范围为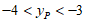 .————6
.————6
27. 解:(1)2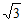 ;
;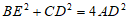 ;
;
(2)作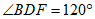 交BA延长线于F,连接AE,作
交BA延长线于F,连接AE,作 交ED延长线于G,连GC,如图:
交ED延长线于G,连GC,如图:
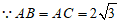 ,
,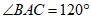 ,
,
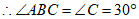 ,
,
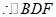 ,
,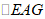 ,
,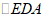 都是顶角为
都是顶角为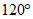 的等腰三角形,
的等腰三角形,
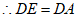 ,
,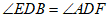 ,
,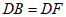 ,
,
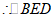 ≌
≌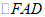 ,
,
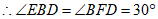 ,
,
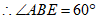 同理
同理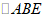 ≌
≌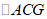 ,
,
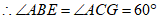 ,
,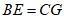 ,
,
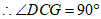 ,
,
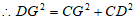 ,
,
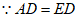 ,
,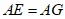 ,
,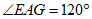 ,
,
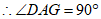 ,则
,则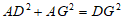 ,
,
且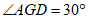 ,则
,则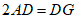 ,
,
可知: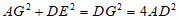 ,
,
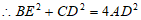 .
.
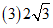 .——————7
.——————7
28. (1)①是,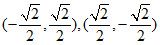 .
.
②由题意可知,直线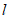 的所有同类点组成平行于直线
的所有同类点组成平行于直线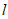 ,且到直线
,且到直线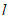 的距离为
的距离为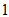 的直线.
的直线.
设该直线与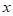 轴交于点
轴交于点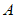 ,与
,与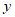 轴交于点
轴交于点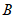 .
.
如图,当点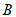 在原点上方时,作
在原点上方时,作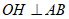 于点
于点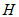 ,
,
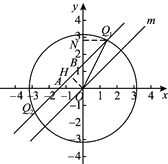
可知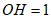 .
.
由直线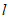 的表达式为
的表达式为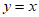 ,可知
,可知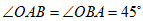 .
.
所以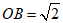 .
.
直线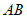 与
与 的交点即为满足条件的点
的交点即为满足条件的点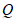 .
.
连接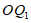 ,作
,作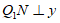 轴于点
轴于点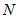 ,可知
,可知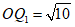 .
.
在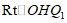 中,可求
中,可求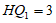 .
.
所以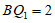 .
.
在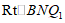 中,可求
中,可求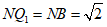 .
.
所以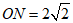 ,
,
所以点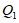 的坐标为
的坐标为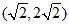 .
.
同理可求点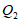 的坐标为
的坐标为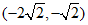 .
.
如图,
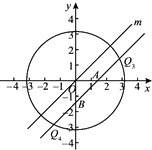
当点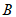 在原点下方时,可求点
在原点下方时,可求点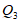 的坐标为
的坐标为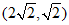 ,点
,点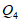 的坐标为
的坐标为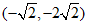 .
.
综上所述,点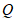 的坐标为
的坐标为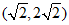 ,
,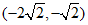 ,
,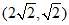 ,
,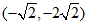 .
.
(2)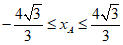 . ————————7
. ————————7