(本试卷满分120分,考试时间100分钟)
一、选择题:共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 设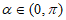 ,且
,且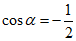 ,则
,则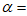 (
(
)
A. 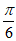 B.
B. 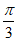 C.
C. 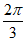 D.
D.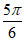
2. 已知复数z满足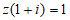 ,则z对应的点位于复平面内的(
,则z对应的点位于复平面内的(
)
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3. 一组数据的平均数为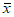 ,方差为s2,将这组数据的每个数都乘以a(a>0)得到一组新数据,则下列说法正确的是(
,方差为s2,将这组数据的每个数都乘以a(a>0)得到一组新数据,则下列说法正确的是(
)
A. 这组新数据的平均数为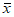 B. 这组新数据的平均数为
B. 这组新数据的平均数为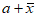
C. 这组新数据的方差为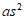 D. 这组新数据的标准差为as
D. 这组新数据的标准差为as
4. 已知随机事件A,B,C中,A与B互斥,B与C对立,且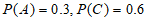 ,则
,则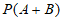 =(
=(
)
A. 0.3 B. 0.6 C. 0.7 D. 0.9
5. 已知单位向量 满足
满足 ,若向量
,若向量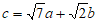 ,则
,则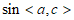 =(
=(
)
A. 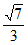 B.
B. 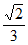 C.
C. 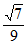 D.
D.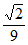
6. 在△ABC中,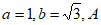 =30°,则c=(
=30°,则c=(
)
A. 1 B. 2 C. 1或2 D. 无解
7. 设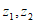 是复数,则”
是复数,则”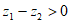 “是”
“是”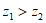 “的(
“的(
)
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
8. 函数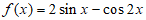 在区间
在区间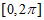 上的零点个数为(
上的零点个数为(
)
A. 2 B. 3 C. 4 D. 5
9. 下列结论正确的是(
)
A. 若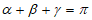 ,则
,则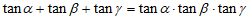
B. 设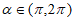 ,则
,则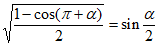
C. 设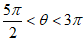 ,且
,且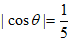 ,那么
,那么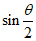 的值为
的值为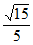
D. 存在实数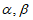 ,使等式
,使等式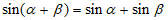 成立
成立
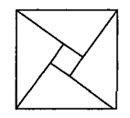
10. 我国古代数学家赵爽的弦图是有四个全等的直角三角形与一个小正方形拼成的大正方形(如图),如果小正方形的边长为2,大正方形的边长为10,直角三角形中较小的锐角为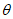 ,则
,则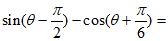 (
(
)
A. 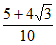 B.
B. 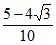 C.
C. 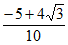 D.
D.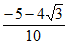
二、填空题:共6小题,每小题5分,共30分。
11. 已知五个数1,2,3,4,a的平均数是3,则这五个数的标准差是_____________。
12. 已知复数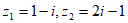 ,则复数
,则复数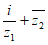 的虚部等于____________。
的虚部等于____________。
13. 暑假期间,甲外出旅游的概率是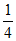 ,乙外出旅游的概率是
,乙外出旅游的概率是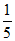 ,假定甲乙两人的行动相互之间没有影响,则暑假期间两人中至少有一人外出旅游的概率是____________。
,假定甲乙两人的行动相互之间没有影响,则暑假期间两人中至少有一人外出旅游的概率是____________。
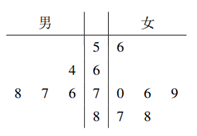
14. 某学校开展了“国学“系列讲座活动,为了了解活动效果,用分层抽样的方法从高一年级所有学生中抽取10人进行国学素养测试,这10名同学的性别和测试成绩(百分制)的茎叶图如图所示,则男生成绩的75%分位数为___________;已知高一年级中男生总数为80人,试估计高一年级学生总数为__________。
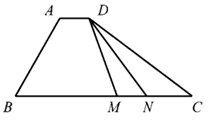
15. 如图,在四边形ABCD中,∠B=60°,AB=3,BC=6,且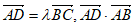 =
=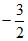 ,则实数
,则实数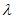 的值为__________,若M,N是线段BC上的动点,且
的值为__________,若M,N是线段BC上的动点,且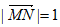 ,则
,则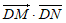 的最小值为____________。
的最小值为____________。
16. 已知点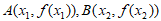 是函数
是函数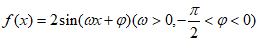 图像上的任意两点,角
图像上的任意两点,角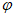 终边经过点
终边经过点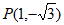 ,且当
,且当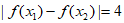 时,
时,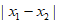 的最小值为
的最小值为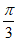 ,若
,若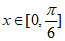 ,不等式
,不等式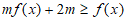 恒成立,则实数m的取值范围是___________。
恒成立,则实数m的取值范围是___________。
三、解答题:共4小题,共50分。解答应写出文字说明、演算步骤或证明过程。
17. (本小题12分)
某超市从2019年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取100个,并按[0,10],(10,20],(20,30],(30,40],(40,50]分组,得到频率分布直方图如下:
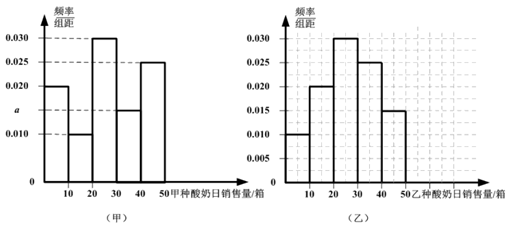
假设甲、乙两种酸奶的日销售量相互独立。
(1)写出频率分布直方图(甲)中的a的值;记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为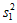 ,
,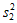 ,试比较
,试比较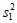 与
与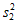 的大小;(只需写出结论)
的大小;(只需写出结论)
(2)用频率估计概率,求在未来的某一天里,甲、乙两种酸奶的销售量恰有一个高于20箱的概率。
18.(本小题12分)
在△ABC中,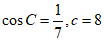 ,再从条件①、条件②这两个条件中选择一个作为已知,求:
,再从条件①、条件②这两个条件中选择一个作为已知,求:
(1)b的值;
(2)角A的大小和△ABC的面积。
条件①: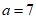 ;
;
条件②: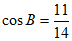 。
。
19. (本小题13分)
在平面直角坐标系中,O为坐标原点,A,B,C三点满足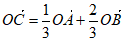 。
。
(1)求证:A,B,C三点共线;
(2)若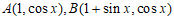 ,且
,且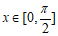 ,函数
,函数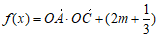
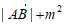 的最小值为5,求实数m的值。
的最小值为5,求实数m的值。
20. (本小题13分)
我们学过二维的平面向量,其坐标为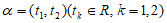 ,那么对于
,那么对于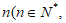
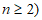 维向量,其坐标为
维向量,其坐标为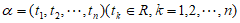 。设
。设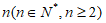 维向量的所有向量组成集合
维向量的所有向量组成集合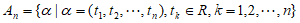 ,当
,当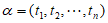
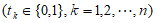 时,称为
时,称为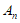 的”特征向量”,如
的”特征向量”,如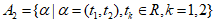 的”特征向量”有
的”特征向量”有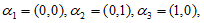
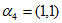 。
。
设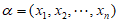 和
和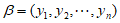 为
为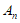 的”特征向量”,
的”特征向量”,
定义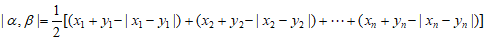 。
。
(1)若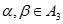 ,且
,且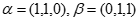 ,计算
,计算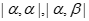 的值;
的值;
(2)设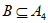 ,且B中向量均为
,且B中向量均为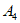 的”特征向量”,且满足:
的”特征向量”,且满足: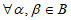 ,当
,当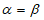 时,
时,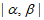 为奇数;当
为奇数;当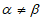 时,
时,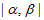 为偶数,求集合B中元素个数的最大值;
为偶数,求集合B中元素个数的最大值;
(3)设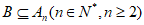 ,且B中向量均为
,且B中向量均为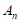 的”特征向量”,且满足:
的”特征向量”,且满足: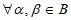 ,且
,且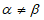 时,
时,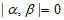 ,写出一个集合B,使其元素最多,并说明理由。
,写出一个集合B,使其元素最多,并说明理由。
【试题答案】
1. C 2. D 3. D 4. C 5. B 6. C 7. B 8. A 9. D 10. D
11. 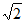 12.
12. 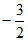 13.
13. 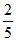 14. 77.5;200 15.
14. 77.5;200 15.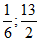
16. 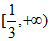
17. (1)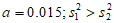 。
。
(2)设事件A为“在未来的某一天里,甲种酸奶的销售量不高于20箱“;
事件B为“在未来的某一天里,乙种酸奶的销售量不高于20箱“;
事件C为“在未来的某一天里,甲、乙两种酸奶的销售量恰有一个高于20箱“。
用频率估计概率,则P(A)=0.020×10+0.010×10=0.3,
P(B)=0.010×10+0.020×10=0.3。
则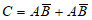 ,
,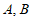 独立,
独立,
所以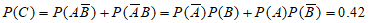 。
。
18. 选择条件①。
(1)因为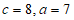 ,
,
由余弦定理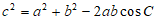 ,得
,得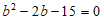 ,
,
解得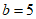 或
或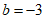 (舍),
(舍),
所以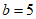 。
。
(2)因为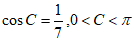 ,
,
所以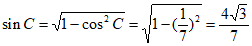 。
。
由正弦定理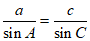 ,得
,得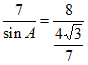 ,
,
所以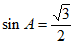 。
。
因为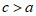 ,所以
,所以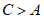 ,所以
,所以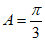 ,
,
所以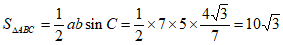 。
。
选择条件②。
(1)因为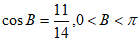 ,
,
所以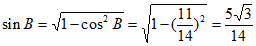 。
。
因为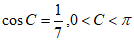 ,
,
所以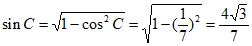 。
。
由正弦定理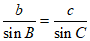 ,得
,得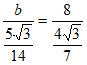 ,
,
解得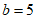 。
。
(2)由(1)知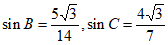 。
。
又因为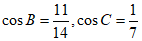 ,
,
在△ABC中,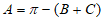 ,
,
所以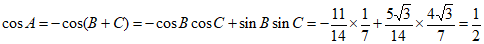 ,
,
所以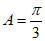 ,
,
所以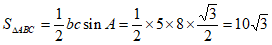 。
。
19.(1)因为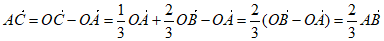 ,
,
所以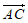 ∥
∥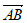 ,又
,又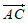 与
与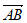 有公共点A,
有公共点A,
所以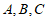 三点共线。
三点共线。
(2)因为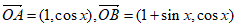 ,
,
所以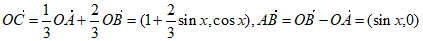 ,
,
故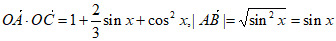 ,
,
从而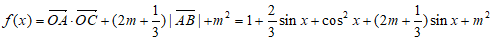
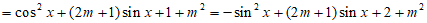 ,
,
关于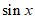 的二次函数的对称轴为
的二次函数的对称轴为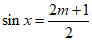 ,
,
因为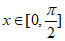 ,所以
,所以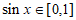 ,又区间
,又区间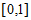 的中点为
的中点为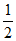 。
。
①当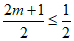 ,即
,即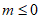 ,当
,当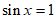 时,
时,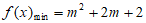 ,
,
由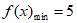 得
得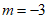 或
或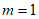 ,又
,又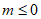 ,所以
,所以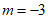 ;
;
②当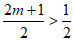 ,即
,即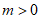 时,当
时,当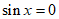 时,
时,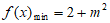 ,
,
由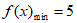 得
得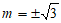 ,又
,又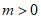 ,所以
,所以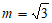 。
。
综上所述:m的值为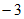 或
或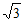 。
。
20.(1)因为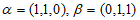 ,所以
,所以
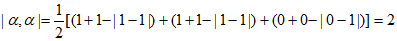 ,
,
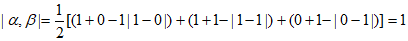 。
。
(2)设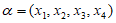
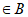 ,则
,则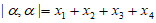 ,
,
由题意知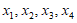
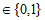 ,且
,且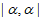 为奇数,
为奇数,
所以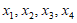 中1的个数为1或3,所以
中1的个数为1或3,所以
B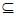 {(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1),(0,1,1,1),(1,0,1,1),(1,1,0,1),(1,1,1,0)}。
{(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1),(0,1,1,1),(1,0,1,1),(1,1,0,1),(1,1,1,0)}。
将上述集合中的元素分成如下四组:
(1,0,0,0),(1,1,1,0);(0,1,0,0),(1,1,0,1);(0,0,1,0),(1,0,1,1);(0,0,0,1),(0,1,1,1)。
经验证,对于每组中两个元素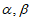 ,均有
,均有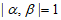 ,
,
所以每组中的两个元素不可能同时是集合B的元素,
所以集合B中元素的个数不超过4。
又集合{(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1)}满足条件,
所以集合B中元素个数的最大值为4。
(3)设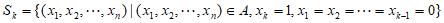
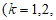
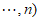 ,
,
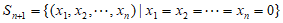 ,
,
则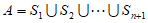 。
。
对于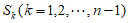 中的不同元素
中的不同元素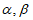 ,经验证,
,经验证,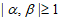 ,
,
所以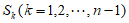 中的两个元素不可能同时是集合B的元素,
中的两个元素不可能同时是集合B的元素,
所以B中元素的个数不超过n+1。
取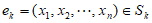 且
且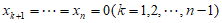 ,
,
令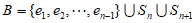 ,则集合B的元素个数为
,则集合B的元素个数为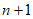 ,且满足条件。
,且满足条件。
故B是一个满足条件且元素个数最多的集合。
