一、选择题(本题共14分,每小题2分)
1.如图是某几何体的三视图,该几何体是
A.三棱柱 B.长方体 C.圆锥 D.圆柱
2.如图,AB//CD,直线EF分别交AB,CD于M,N两点,将一个含有45°角的直角三角尺按如图所示的方式摆放,若∠EMB=75°,则∠PNM等于
A.15° B. 25° C.30° D.45°
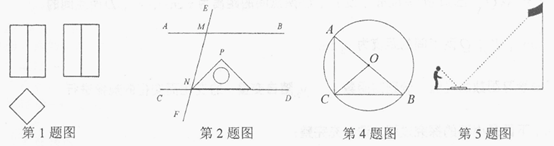
3.用配方法解一元二次方程x2-6x-5=0,此方程可化为
A. (x-3)2=4 B. (x-3)2=14 C. (x-9)2=4 D. (x-9)2=14
4.如图,AB为⊙O的直径,点C在⊙O上,若∠ACO=50°,则∠B的度数为
A.60° B.50° C.40° D.30°
5.如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2m,旗杆底部与平面镜的水平距离为16m.若小明的眼睛与地面的距离为1.5m,则旗杆的高度为(单位:m)
A.
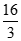 B.9 C.
B.9 C.
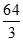 D.12
D.12
6.整数a、b在数轴上对应点的位置如图,实数c在数轴上且满足a≤c≤b,如果数轴上有一实数d,始终满足c+d≥0,则实数d应满足
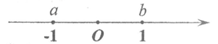
A. d≤a B. a≤d≤ b C. d≤b D. d≥b
7.下图为2009年到2015年中关村国家自主创新示范区企业经营技术收入的统计图.下面四个推断:
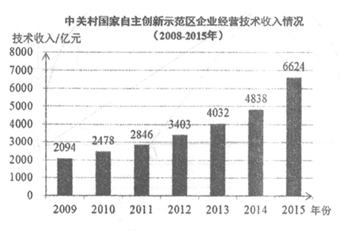
①2009年到2015年技术收入持续增长;
②2009年到2015年技术收入的中位数是4032亿;
③2009年到2015年技术收入增幅最大的是2015年;
④2009年到2011年的技术收入增长的平均数比2013年到2015年技术收入增长的平均数大.其中,正确的是
A.①③ B.①④ C.②③ D.③④
二、填空题(本题共16分,每小题2分)
8.分解因式: ab2 -2ab+a=_______________.
9.一个多边形的内角和是外角和的2倍,则这个多边形的边数为________________.
10.请你写出一个二次函数,其图象满足条件:①开口向上;②与y轴的交点坐标为(0,1).此二次函数的解析式可以是________________.
11.如果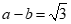 ,那么代数式
,那么代数式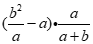 的值为_______________.
的值为_______________.
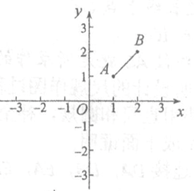
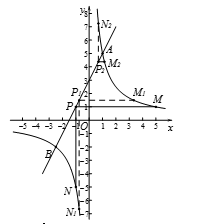
12.如图,在平面直角坐标系xOy中,A (1,1),B(2,2),双曲线 与线段AB有公共点,则k的取值范围是_____________.
与线段AB有公共点,则k的取值范围是_____________.
13.2019年2月,全球首个5G火车站在上海虹桥火车站启动.虹桥火车站中5G网络峰值速率为4G网络峰值速率的10倍.在峰值速率下传输8千兆数据,5G 网络比4G网络快720秒,求这两种网络的峰值速率,设4G网络的峰值速率为每秒传输x千兆数据,依题意,可列方程为_____________.
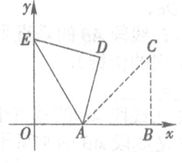
14.如图,在平面直角坐标系xOy中,点A的坐标为A(1,0),等腰直角三角形ABC的边AB在x轴的正半轴上,∠ABC=90°,点B在点A的右侧,点C在第一象限.将△ABC绕点A逆时针旋转75°,如果点C的对应点E恰好落在y轴的正半轴上,那么边AB的长为_____________.
15.将A、B两位篮球运动员在一段时间内的投篮情况记录如下:
投篮次数 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | |
A | 投中次数 | 15 | 23 | 30 | 38 | 45 | 53 | 60 | 68 | 75 |
投中频率 | 0.750 | 0.767 | 0.750 | 0.760 | 0.750 | 0.757 | 0.750 | 0.756 | 0.750 | |
B | 投中次数 | 14 | 23 | 32 | 35 | 43 | 52 | 61 | 70 | 80 |
投中频率 | 0.700 | 0.767 | 0.800 | 0.700 | 0.717 | 0.743 | 0.763 | 0.778 | 0.800 | |
下面有三个推断:
①投篮30次时,两位运动员都投中23次,所以他们投中的概率都是0.767.
②随着投篮次数的增加,A运动员投中频率总在0.750附近摆动,显示出一定的稳定性,可以估计A运动员投中的概率是0.750.
③投篮达到200次时,B运动员投中次数一定为160次.其中合理的是__________.
三、解答题(本题共70分,第16~21题每小题5分,第22题4分,第23、24题6分,25题7分,26题8分,27题9分)
16.计算: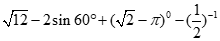 .
.
17.解不等式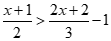 ,并写出它的正整数解.
,并写出它的正整数解.
18. 已知关于x的方程x2-6mx+9m2-9=0.
(1)求证:此方程有两个不相等的实数根;
(2)若此方程的两个根分别为x1,x2,其中x1>x2,若x1=2x2,求m的值.
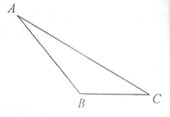
19.下面是小明设计的”作三角形的高线”的尺规作图过程.
已知:△ABC.求作:BC边上的高线。作法:如图,
①分别以A,B为圆心,大于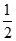 AB长为半径画弧,两弧交于点D,E;
AB长为半径画弧,两弧交于点D,E;
②作直线DE,与AB交于点F,以点F为圆心,FA长为半径画圆,交CB的延长线于点G;
③连接AG.
所以线段AG就是所求作的BC边上的高线.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形; (保留作图痕迹)
(2)完成下面证明.
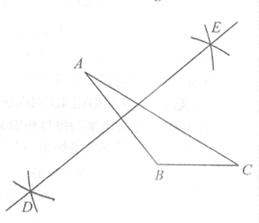
证明:连接DA,DB,EA,EB,
∵DA=DB,
∴点D在线段AB的垂直平分线上(____________________________)
(填推理的依据).
∵________=_________,
∴点E在线段AB的垂直平分线上.
∴DE是线段AB的垂直平分线.
∴FA=FB.
∴AB是⊙F的直径.
∴∠AGB=90° (_________________________)(填推理的依据).
∴AG⊥BC即AG就是BC边上的高线.
20.某年级共有300名学生.为了解该年级学生A,B两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
a.A课程成绩的频数分布直方图如下(数据分成6组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):
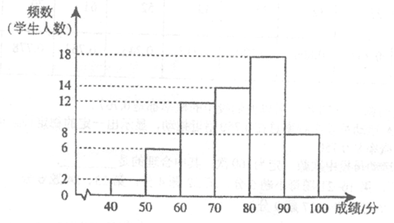
b.A课程成绩在70≤x<80这一组的是:
70 71 71 71 76 76 77 78 78.5 78.5 79 79 79 79.5
c.A,B两门课程成绩的平均数、中位数、众数如下:
课程 | 平均数 | 中位数 | 众数 |
A | 75.8 | m | 84.5 |
B | 72.2 | 70 | 83 |
根据以上信息,回答下列问题:
(1)写出表中m的值;
(2)在此次测试中,某学生的A课程成绩为76分,B课程成绩为71分,这名学生成绩排名更靠前的课程是_________(填”A”或”B”),理由是____________.
(3)假设该年级学生都参加此次测试,估计A课程成绩超过75.8分的人数.
21.△ABC中,AB=AC,D为 BC中点,AE//BD,且AE=BD.
(1)求证:四边形AEBD是矩形。
(2)连接CE交AB于点F,若∠ABE=30°,AE=2,求EF的长.

22.如图,C是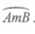 上的一定点,D是弦AB上的一定点,P是弦CB上的一动点,连接DP,将线段PD绕点P顺时针旋转90°得到线段PD’ ,射线PD’与
上的一定点,D是弦AB上的一定点,P是弦CB上的一动点,连接DP,将线段PD绕点P顺时针旋转90°得到线段PD’ ,射线PD’与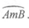 交于点Q.已知BC=6cm,设P,C两点间的距离为xcm,P,D两点间的距离为y1cm,P,Q两点间的距离为y2cm.
交于点Q.已知BC=6cm,设P,C两点间的距离为xcm,P,D两点间的距离为y1cm,P,Q两点间的距离为y2cm.
小石根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,y2,与x的几组对应值:
x/ cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 4.29 | 3.33 | 1.65 | 1.22 | 1.50 | 2.24 | |
y2/cm | 0.88 | 2.84 | 3.57 | 4.04 | 4.17 | 3.20 | 0.98 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数据所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;
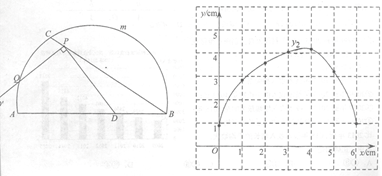
(3)结合函数图象,解决问题:连接DQ,当△DPQ为等腰三角形时,PC的长度约为_________________cm.(结果保留一位小数)
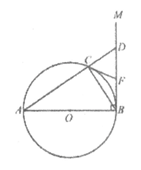
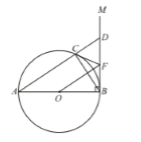
23.如图,AB为⊙O的直径,直线BM⊥AB于点B.点C在⊙O上,分别连接BC,AC,且AC的延长线交BM于点D.CF为⊙O的切线交BM于点F.
(1)求证:CF= DF;
(2)连接OF.若AB=10,BC=6,求线段OF的长.
24.在平面直角坐标系xoy中,直线y=2x+b与双曲线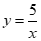 交于A、B两点,P是线段AB上一点(不与A、B重合),过点P作平行于x轴的直线交双曲线
交于A、B两点,P是线段AB上一点(不与A、B重合),过点P作平行于x轴的直线交双曲线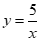 于点M,过点P作平行于y轴的直线交双曲线
于点M,过点P作平行于y轴的直线交双曲线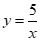 于点N.
于点N.
(1)当点A的横坐标为1时,则b的值为___________;
(2)在(1)的条件下,设P点的横坐标为m.
①若m=-1,判断PM与PN的数量关系,并说明理由;
②若PM<PN,结合函数图象,直接写出m的取值范围是____________.
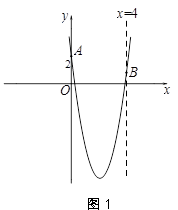
25.平面直角坐标系xOy中,抛物线y=mx2 -2m2x+2交y轴于A点,交直线x=4于B点. (1)抛物线的对称轴为x=_____(用含 m的代数式表示);
(2)若AB∥x轴,求抛物线的表达式;
(3)记抛物线在A,B之间的部分为图象G(包含A,B两点),若对于图象G上任意一点P(xp,yp),yp≤2,请直接写出m的取值范围是__________.
26.对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若存在过点P的直线l交⊙C于异于点P的A,B两点,在P,A,B三点中,位于中间的点恰为以另外两点为端点的线段的中点时,则称点P为⊙C的相邻点,直线l为⊙C关于点P的相邻线.
(1)当⊙O的半径为1时,
①判断点D (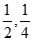 )______(填”是”或”不是”)⊙O的相邻点,如果是请在图1中做出⊙O关于它的一条相邻线,并说明你的作图过程,如果不是请说明理由.
)______(填”是”或”不是”)⊙O的相邻点,如果是请在图1中做出⊙O关于它的一条相邻线,并说明你的作图过程,如果不是请说明理由.
②分别判断E(0,-3),F(4,0),G(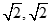 )中,是⊙O的相邻点有_________.
)中,是⊙O的相邻点有_________.
③点P在直线y=-x+3上,若点P为⊙O的相邻点,求点P横坐标的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线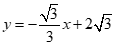 与x轴,y轴分别交于点M,N,若线段MN上存在⊙C的相邻点P,直接写出圆心C的横坐标的取值范围.
与x轴,y轴分别交于点M,N,若线段MN上存在⊙C的相邻点P,直接写出圆心C的横坐标的取值范围.
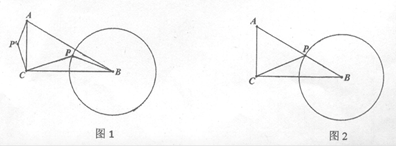
27.如图1,在△4BC中,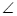 ACB=90°,AC=2,BC=
ACB=90°,AC=2,BC=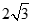 ,以点B为圆心,
,以点B为圆心,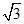 为半径作圆.点P为⊙B上的动点,连接PC,作P’C⊥PC,使点P’落在直线BC的上方,且满足P’C:PC=
为半径作圆.点P为⊙B上的动点,连接PC,作P’C⊥PC,使点P’落在直线BC的上方,且满足P’C:PC=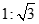 ,连接BP,AP’.
,连接BP,AP’.
(1)求∠BAC的度数,并证明△AP’C∽△BPC;
(2)若点P在AB上时,①在图2中画出△AP’C;②连接BP’,求BP’的长;
(3)点P在运动过程中,BP’ 是否有最大值或最小值?若有,请直接写出BP’取得最大值或最小值时∠PBC的度数;若没有,请说明理由.
参考答案
1—15题,每题2分,共30分
1. B 2.C 3.B 4.C 5.D 6.D 7.A
8.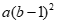 9. 6 10.
9. 6 10.  11.
11. 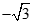 12.
12.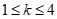
13. 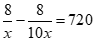 14.
14. 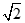 15. ②
15. ②
16.计算: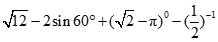
解:原式=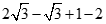 …………4分
…………4分
=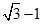 . …………5分
. …………5分
17. 解: 去分母得:3(x+1)>2(2x+2)﹣6, …………1分
去括号得:3x+3>4x+4﹣6, …………2分
移项得:3x﹣4x>4﹣6﹣3, …………3分
合并同类项得:﹣x>﹣5,
系数化为1得:x<5. …………4分
故不等式的正整数解有1,2,3,4这4个. …………5分
18.(1)∵△=(-6m)2-4(9m2-9) ……………………………………………………1分
=36m2-36m2+36
=36>0.
∴方程有两个不相等的实数根…………………………………………………2分
(2)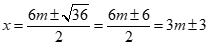 .……………………………………3分
.……………………………………3分
∵3m+3>3m-3,
∴x1=3m+3,x2=3m-3, ……………………………………………………………4分
∴3m+3=2(3m-3) .
∴m=3. ………………………………………………………………………………5分
19.解:(1)使用直尺和圆规,补全图形;(保留作图痕迹)
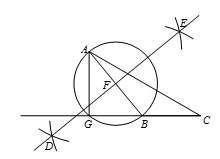
……………………………2分
(2)到线段两个端点距离相等的点在这条线段的垂直平分线上………3分
EA=EB ……………………………………………………………………………4分
直径所对的圆周角是直角 …………………………………………………………5分
20.(1)78.75……………………………………1分
(2)B…………………………………2分
这名学生A课程成绩是76,比中位数78.75低,说明排名在30名后;而他的B课程成绩是71,比中位数70要高,说明排名在30名之前,所以B课程排名靠前。………3分
(3) 180人 ……………………………5分
21.(1)…………………………3分
(2)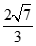 …………………5分
…………………5分
22. 解:本题答案不唯一,如:
(1)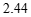 ;
;
……………………………1分
(2)
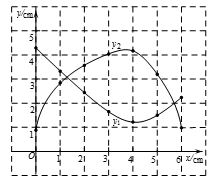
……………………………2分
(3)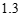 或
或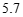 .
.
……………………………4分
23. (1)证明:∵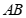 是
是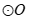 的直径,
的直径,
∴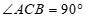 .
.
∴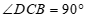 .
.
∴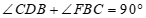 .
.
∵
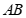 是
是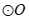 的直径,
的直径,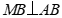 ,
,
∴MB是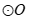 的切线.
的切线.
∵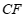 是
是 的切线,
的切线,
∴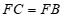 .
.
∴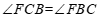 .
.
∵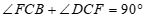 ,
,
∴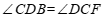 .
.
∴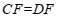 . ———————————-3分
. ———————————-3分
(2)由(1)可知,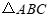 是直角三角形,在
是直角三角形,在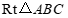 中,
中,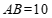 ,
,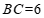 ,
,
根据勾股定理求得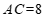 .
.
在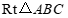 和
和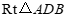 中,
中,
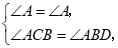
∴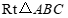 ∽
∽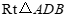 .
.
∴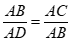 .∴
.∴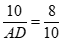 .∴
.∴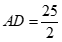 .
.
由(1)知,
∵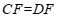 ,
,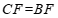 ,
,
∴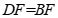 .
.
∵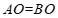 ,
,
∴
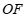 是
是 的中位线.
的中位线.
∴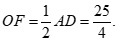 ————————————–6分
————————————–6分
24.解:(1)∵当点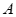 的横坐标为1,点
的横坐标为1,点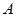 在双曲线
在双曲线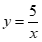 上,
上,
∴点 的纵坐标为
的纵坐标为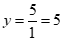 .…………………………1分
.…………………………1分
将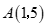 代入
代入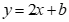 ,得
,得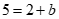 ,∴
,∴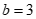 .………………2分
.………………2分
(2)①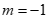 时,将
时,将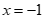 代入
代入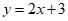 ,得
,得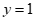 .
.
∴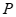 点的坐标为
点的坐标为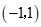 .……………………………3分
.……………………………3分
将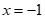 代入
代入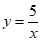 ,得
,得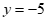 ,将
,将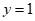 代入
代入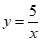 ,得
,得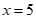 ,
,
∴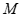 点的坐标为
点的坐标为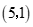 ,
,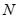 点的坐标为
点的坐标为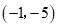 .
.
∴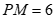 ,
,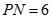 .
.
∴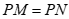 .………………………………………4分
.………………………………………4分
②若PM<PN,结合函数图象得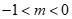 或
或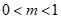 .……6分
.……6分
25. (1)m;—————————————————-2分
(2)∵ 抛物线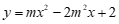 与y轴交于A点,
与y轴交于A点,
∴
A(0,2).————————— 3分
∵
AB∥x轴,B点在直线x=4上,
∴
B(4,2),抛物线的对称轴为直线x=2. ————— 4分
∴
m=2.
∴抛物线的表达式为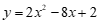 . ——— 5分
. ——— 5分
(3)当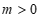 时,如图1.
时,如图1.
∵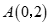 ,
,
∴要使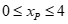 时,始终满足
时,始终满足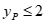 ,
,
只需使抛物线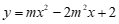 的对称轴与直线x=2重合或在直线x=2的右侧.
的对称轴与直线x=2重合或在直线x=2的右侧.
∴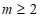 . ——————— 6分
. ——————— 6分
当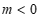 时,如图2,
时,如图2,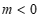 时,
时,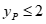 恒成立. —— 7分
恒成立. —— 7分
综上所述,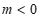 或
或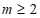 .
.
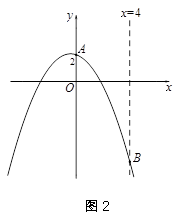
26. (1)60°—————- 1分 证明相似———— 3分
(2)画图正确——– 4分 BP’值为 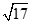 —– 6分
—– 6分
(3)最大值时∠PBC=120°———— 7分 最小值时∠PBC=60°——— 8分
27. (1)①是—- 1分 画图———– 2分(通过构造垂径定理作图)
② E、G — 4分(少写一个扣1分,有错误答案不给分)
③ 0≤x≤3——– 7分(过程2分)
(2)0≤x≤9—————————- 9分
