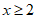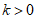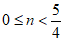(考试时间:100分钟
满分:100分)
一、选择题:本大题共10小题,每题3分,共30分。
1. 下列曲线中,表示y是x的函数的是(
)
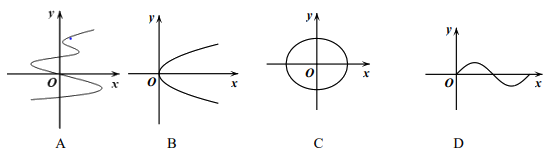
2. 下列四组线段中,可以构成直角三角形的是(
)
A. 1,1,1 B. 2,3,4 C. 5,12,13 D. 1,2,3
3. 下列二次根式中,最简二次根式是(
)
A. 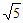 B.
B. 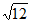 C.
C. 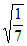 D.
D.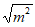
4. 如图,矩形ABCD中,对角线AC、BD相交于点O,若AB=2,∠AOB=60°,则AC的长度为(
)
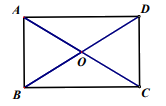
A. 2 B. 3 C. 4 D. 6
5. 如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AM的长为1.2km,则M、C两点间的距离为(
)km
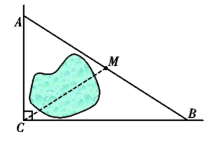
A. 0.5B. 0.6 C. 0.9 D. 1.2
6. 把函数y=x的图象向上平移2个单位,下列各点在平移后的函数图象上的是(
)
A. (2,2) B. (2,3) C. (2,4) D. (2,5)
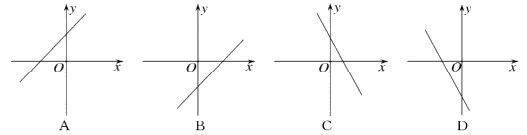
7. 一次函数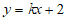 中,若
中,若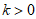 ,则其图象可能是(
,则其图象可能是(
)
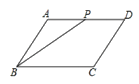
8. 如图,点P是平行四边形ABCD边上一动点,沿A→D→C→B的路径移动,设P点经过的路径长为x,△BAP的面积是y,则下列能大致反映y与x的函数关系的图象是
(
)
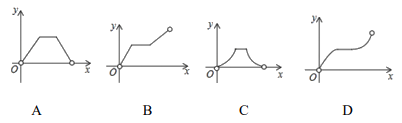
9. 如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=6,F为DE的中点,若OF的长为1,则△CEF的周长为(
)
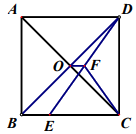
A. 14 B. 16 C. 18 D. 12
10. 直线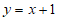 与
与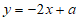 的交点在第一象限,则a的取值可以是(
的交点在第一象限,则a的取值可以是(
)
A. -1 B. 0 C. 1 D. 2
二、填空题:本大题共7小题,11—16题,每题3分,17题4分,共22分。
11. 函数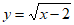 中自变量x的取值范围是____________。
中自变量x的取值范围是____________。
12. 若正比例函数y=kx(k是常数,k≠0)的图象经过第一、三象限,请写出一个满足上述要求的k的值_____________。
13. 如图,一棵高为16m的大树被台风刮断,若树在离地面6m处折断,树顶端刚好落在地面上,此处离树底部___________m处。
14. 如图,在平行四边形ABCD中,BC=8cm,AB=6cm,BE平分∠ABC交AD边于点E,则线段DE的长度为____________cm。
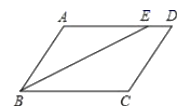
15. 如图,在正方形ABCD中,等边△AEF的顶点E,F分别在边BC和CD上,则∠AEB=_____________°。
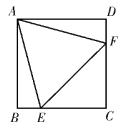
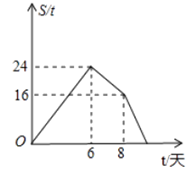
16. 春耕期间,某农资门市部连续8天调进一批化肥,从调进化肥的第7天开始销售,若进货期间每天调入化肥的吨数与销售期间每天销售化肥的吨数都保持不变,这个门市部的化肥存量S(单位:t)与时间t(单位:天)之间的函数关系如图所示,则该门市部这次化肥销售活动(从开始进货到销售完毕)所用时间是___________天。
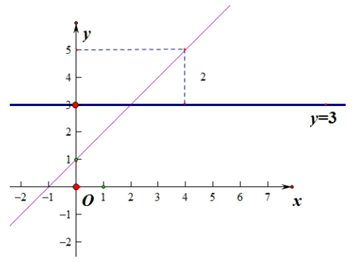
17. 在平面直角坐标系xOy中,过点A(5,3)作y轴的平行线,与x轴交于点B,直线y=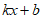 (
(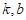 为常数,
为常数,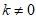 )经过点A且与x轴交于点C(9,0),我们称横、纵坐标都是整数的点为整点。
)经过点A且与x轴交于点C(9,0),我们称横、纵坐标都是整数的点为整点。
(1)记线段AB,BC,CA围成的区域(不含边界)为W,请你结合函数图象,则区域W内的整点个数为________________;
(2)将直线y=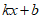 向下平移n个单位(n≥0),若平移后的直线与线段AB,BC围成的区域(不含边界)存在整点,请结合图象写出n的取值范围_________________。
向下平移n个单位(n≥0),若平移后的直线与线段AB,BC围成的区域(不含边界)存在整点,请结合图象写出n的取值范围_________________。
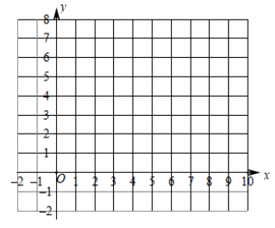
三、解答题:本大题共8小题,第18题6分,第19、20、21题,每题5分,第22题6分,第23、24、25题,每题7分,共48分。
18. 计算:
(1)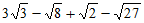
(2)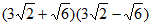
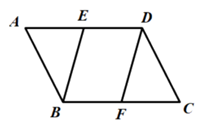
19. 已知点E、F分别为平行四边形ABCD的边AD、BC的中点,求证:四边形EBFD为平行四边形。
20. 已知y与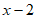 成正比例,且当
成正比例,且当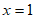 时,
时,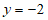
(1)求变量y与x的函数关系式;
(2)请在给出的平面直角坐标系中画出此函数的图象;
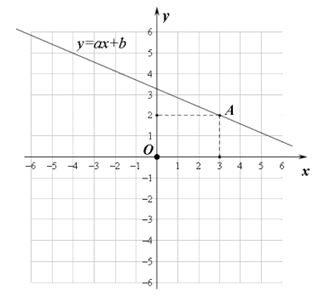
(3)已知点A在函数y=ax+b的图象上,请直接写出关于x的不等式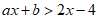 的解集______________。
的解集______________。
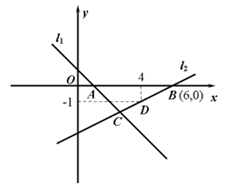
21. 如图,直线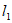 的函数解析式为
的函数解析式为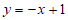 ,且
,且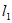 与x轴交于点A,直线
与x轴交于点A,直线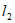 经过点B,D,直线
经过点B,D,直线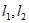 交于点C。
交于点C。
(1)求直线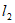 的函数解析式;
的函数解析式;
(2)求△ABC的面积。
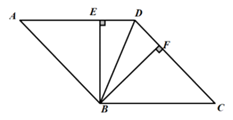
22. 如图,在平行四边形ABCD中,BE⊥AD,BF⊥CD,垂足分别为E,F,且AE=CF
(1)求证:平行四边形ABCD是菱形;
(2)若DB=10,AB=13,求平行四边形ABCD的面积。
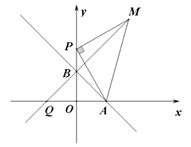
23. 如图,平面直角坐标系xOy中,点A、B的坐标分别为A(a,0),B(0,b),其中a,b满足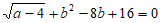 ,点P在y轴上,且在B点上方,
,点P在y轴上,且在B点上方,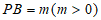 ,以AP为边作等腰直角△APM,∠APM=90°,PM=PA,点M落在第一象限。
,以AP为边作等腰直角△APM,∠APM=90°,PM=PA,点M落在第一象限。
(1)a=____________;b=__________;
(2)求点M的坐标(用含m代数式表示);
(3)若射线MB与x轴交于点Q,判断点Q的坐标是否随m的变化而变化,若不变,求出Q点的坐标;若变化,请说明理由。
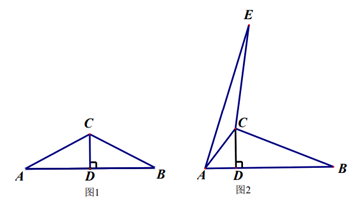
24. 在△ABC中,CD⊥AB于点D。
(1)如图1,当点D是线段AB中点时,延长AC至点E,使得CE=CB,连接EB。
①按要求补全图1;
②若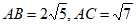 ,求EB的长。
,求EB的长。
(2)如图2,当点D不是线段AB的中点时,作∠BCE(点E与点D在直线BC的异侧),使∠BCE=2∠CAB,CE=CB,连接AE,用等式表示线段AB,CD,AE的数量关系,并说明理由。
25. 对于平面直角坐标系xOy中的图形M和点P,给出如下定义:如果图形M上存在点Q,使得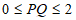 ,那么称点P为图形M的和谐点,已知点
,那么称点P为图形M的和谐点,已知点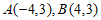
(1)在点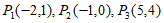 中,直线AB的和谐点是___________;
中,直线AB的和谐点是___________;
(2)点P为直线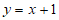 上一点,若点P为直线AB的和谐点,求点P的横坐标t的取值范围;
上一点,若点P为直线AB的和谐点,求点P的横坐标t的取值范围;
(3)已知点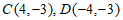 ,如果直线
,如果直线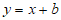 上存在矩形ABCD的和谐点E,F,使得线段EF上的所有点都是矩形ABCD的和谐点,且
上存在矩形ABCD的和谐点E,F,使得线段EF上的所有点都是矩形ABCD的和谐点,且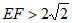 ,请直线写出b的取值范围。
,请直线写出b的取值范围。
【试题答案】
一、选择题:本大题共10小题,每题3分,共30分。
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | D | C | A | C | D | C | A | A | B | D |
二、填空题:本大题共7小题,11—16题,每题3分,17题4分,共22分。
11 | 12 | 13 | 14 | 15 | 16 | 17 | |
|
| 8 | 2 | 75 | 10 | 3个 |
|
三、解答题:本大题共8小题,第18题6分,第19、20、21题,每题5分,第22题6分,第23、24、25题,每题7分,共48分。
18.(1)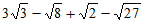
(2)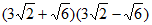
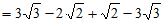 2分
2分
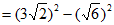 2分
2分
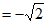 3分
3分
=12 3分
19. ∵平行四边形ABCD
∴AD∥BC,AD=BC 2分
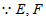 为平行四边形ABCD的中点,
为平行四边形ABCD的中点,
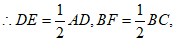 DE∥BF,
DE∥BF,
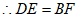 , 4分
, 4分
∴四边形EBFD是平行四边形 5分
20. 解:(1)设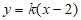 1分
1分
∵当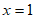 时,
时,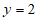 ,
,
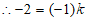
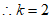 2分
2分
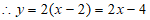 3分
3分
(2)如图 4分
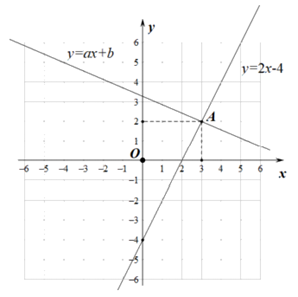
(3)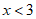 5分
5分
21. 解:(1)设直线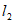 的函数解析式为
的函数解析式为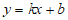
∵直线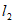 经过点
经过点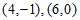
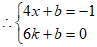 1分
1分
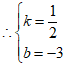
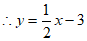 2分
2分
(2)令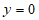 ,则
,则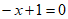 ,得
,得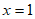 ,
,
∴点A的坐标为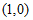 3分
3分
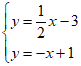 解得
解得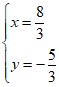 4分
4分
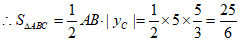 5分
5分
22. (1)证明:∵四边形ABCD为平行四边形
∴∠A=∠C 1分
∵BE⊥AD,BF⊥CD,
∴∠BEA=∠BFC=90°
在△AEB和△CFB中
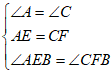
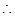 △AEB≌△CFB(ASA)
△AEB≌△CFB(ASA)
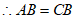 3分
3分
∴平行四边形ABCD为菱形。
(2)连接AC,与BD相交于点O,
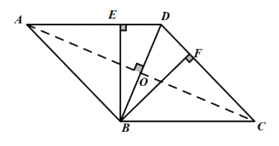
∵平行四边形ABCD为菱形
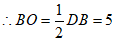 ,∠BOA=90° 4分
,∠BOA=90° 4分
在Rt△ABO中,由勾股定理,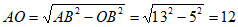 5分
5分
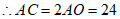
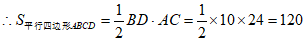 6分
6分
23. 解:(1)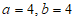 2分
2分
(2)作MN⊥y轴于点N。
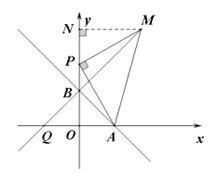
∵APM为等腰直角三角形,PM=PA,
∴∠APM=90°,
∴∠OPA+∠NPM=90°,
∵∠NMP+∠NPM=90°,
∴∠OPA=∠NMP。
又∵∠AOP=∠PNM=90°,
∴△AOP≌△PNM,(AAS)
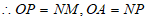 ,
,
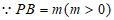 ,
,
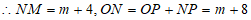 。
。
∵点M在第一象限,
∴点M的坐标为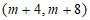 。 5分
。 5分
(3)答:点Q的坐标不变,点Q的坐标都为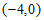 。 6分
。 6分
设直线MB的解析式为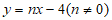 ,
,
∵点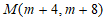 ,在直线MB上,
,在直线MB上,
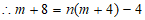 ,整理,
,整理,
得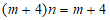 ,
,
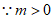 ,
,
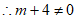 ,解得
,解得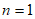 ,
,
∴直线MB的解析式为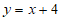 ,
,
∴无论m的值如何变化,点Q的坐标都为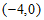 。 7分
。 7分
24. 解:(1)①解:按要求补全图形,如图。 1分
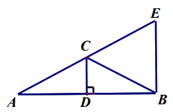
②解:
∵CD⊥AB,D是AB中点
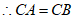
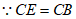
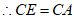 ,
,
∴CD∥BE 3分
∴BE⊥AB
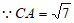
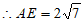
在Rt△ABE中,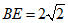
(2)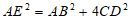 4分
4分
作∠ACM=∠BCE,在射线CM上截取CF=CA,连接BF,AF,
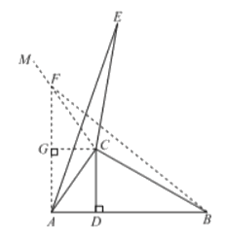
∴∠ACM=∠FCE=∠BCE+∠FCE,即∠ACE=∠FCB,
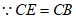 ,
,
∴△ACE≌△FCB(SAS),
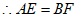 。 5分
。 5分
过点C作CG⊥AF于点G,
∴∠CGF=90°,
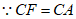 ,
,
∴∠ACF=2∠ACG,AF=2AG,
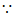 ∠BCE=2∠BAC,
∠BCE=2∠BAC,
∴∠ACG=∠BAC,
∴CG∥AD。
∴∠AGC=∠BAF=∠ADC=90°,
∴四边形ADCG是矩形,
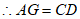 ,
,
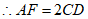
在Rt△BAF中,∠BAF=90°
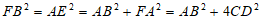 7分
7分
25.(1)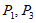 2分
2分
(2)解:如图,若点P在直线上方,则与直线不超过2个单位,此时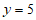 ,代入解析式,得
,代入解析式,得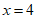 ;若点P在直线下方,同理可得,此时
;若点P在直线下方,同理可得,此时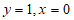 ;所以
;所以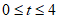 5分
5分
(3)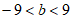 7分
7分