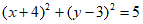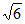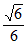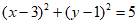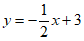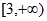试卷分为两卷,卷(I)100分,卷(Ⅱ)50分,满分共计150分
考试时间:120分钟
卷(I)
一、选择题:本大题共10小题,每小题4分,共40分
1. 已知向量 =(1,2,-1),则下列向量与
=(1,2,-1),则下列向量与 垂直的是( )
垂直的是( )
A. (0,0,1) B. (-2,1,0) C. (1,1,2) D. (4,-1,1)
2. 若直线l1:2x+ay+1=0与直线l2:x-2y+2=0平行,则a=( )
A. 1 B. -1 C. 4 D. -4
3. 已知m,n表示两条不同直线,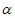 表示平面。下列说法正确的是( )
表示平面。下列说法正确的是( )
A. 若m∥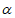 ,n∥
,n∥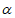 ,则m∥n
,则m∥n
B. 若m⊥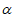 ,n
,n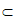
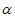 ,则m⊥n
,则m⊥n
C. 若m⊥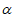 ,m⊥n,则n∥
,m⊥n,则n∥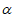
D. 若m∥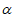 ,m⊥n,则n⊥
,m⊥n,则n⊥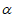
4. 在三棱锥A-BCD中,若AD⊥BC,AD⊥BD,那么必有( )
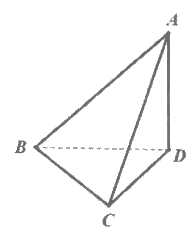
A. 平面ADC⊥平面BCD B. 平面ABC⊥平面BCD
C. 平面ABD⊥平面ADC D. 平面ABD⊥平面ABC
5. 圆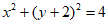 与直线
与直线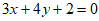 相交于A,B两点,则线段AB的垂直平分线的方程是( )
相交于A,B两点,则线段AB的垂直平分线的方程是( )
A. 4x+3y+6=0 B. 3x+4y+8=0
C. 4x-3y-6=0 D. 4x-3y+6=0
6. 若A(-2,3),B(3,-2),C(1,m)三点共线,则m的值为( )
A. 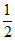 B. -1 C. -2 D. 0
B. -1 C. -2 D. 0
7. 下列命题正确的是( )
A. 若两条直线和同一个平面所成的角相等,则这两条直线平行
B. 若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行
C. 若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行
D. 若两个平面都垂直于第三个平面,则这两个平面平行
8. 如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( )
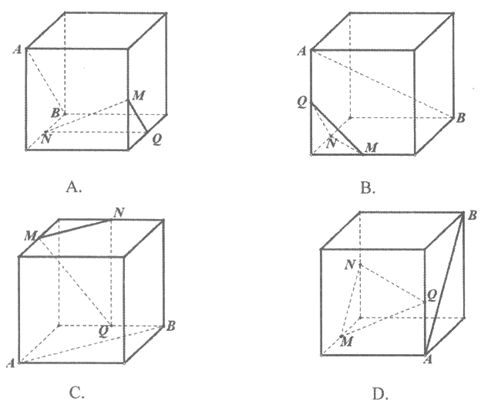
9. 直线kx-y+2k+1=0与x+2y-4=0的交点在第四象限,则k的取值范围为( )
A. (-6,-2) B. (-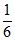 ,0) C. (-
,0) C. (-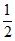 ,-
,-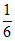 ) D. (-
) D. (-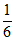 ,
,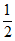 )
)
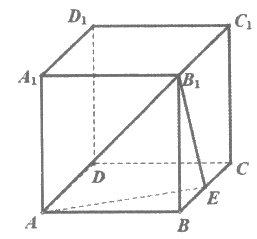
10. 斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在底面ABC上的射影H必在( )
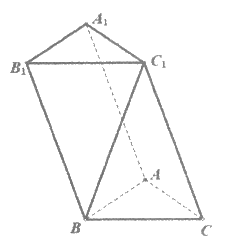
A. 直线AB上 B. 直线BC上
C. 直线AC上 D. △ABC内部
二、填空题:本大题共6小题,每小题4分,共24分
11. 过A(1,0),B(0,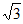 )两点的直线的倾斜角为_________。
)两点的直线的倾斜角为_________。
12. 圆心为C(-4,3)且与直线2x+y+10=0相切的圆的方程为_________。
13. 圆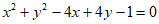 截直线x-y-6=0所得弦长等于_________。
截直线x-y-6=0所得弦长等于_________。
14. 若空间向量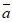 =(5,3,m),
=(5,3,m),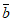 =(1,-1,2),
=(1,-1,2),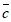 =(0,2,-3)共面,则m=_________。
=(0,2,-3)共面,则m=_________。
15. 棱长为1的正方体ABCD-A1B1C1D1中,E为BC中点,则点B到平面AB1E的距离为__________。
16. 三棱锥O-ABC中,OA,OB,OC两两垂直,且OA=OB=OC。给出下列四个命题:
①(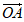 +
+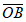 +
+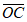 )2=3(
)2=3(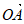 )2;
)2;
②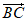 ·(
·(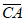 –
–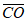 )=0;
)=0;
③(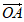 +
+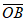 )和
)和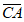 的夹角为60°;
的夹角为60°;
④三棱锥O-ABC的体积为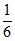 |(
|(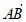 ·
·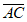 )
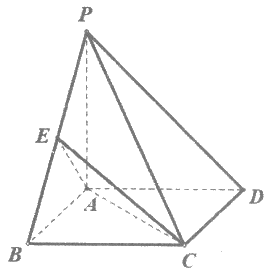
)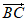 |。其中所有正确命题的序号为________。
|。其中所有正确命题的序号为________。
三、解答题:本大题共3小题,共36分
17.(10分)如图,在直三棱柱ABC-A1B1C1中,AC=CC1,AC⊥BC,D为BC1中点。AC1与A1C交于点O。
(1)求证:OD∥平面A1B1C1;
(2)求证:平面AC1B⊥平面A1BC。
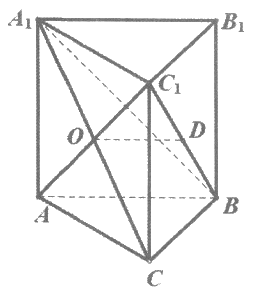
18. (14分)如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AB=AP,E为棱PB的中点。
(1)求直线PD与CE所成角的余弦值;
(2)求直线CD与平面ACE所成角的正弦值;
(3)求二面角E-AC-P的余弦值。
19. (12分)已知直角三角形ABC的顶点坐标A(-4,0),直角顶点B(-2,-2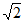 ),顶点C在x轴上。
),顶点C在x轴上。
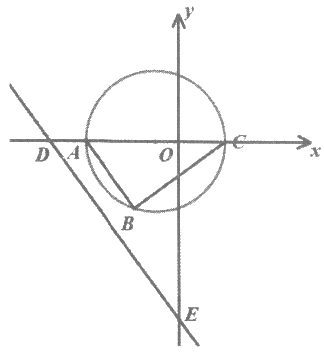
(1)求BC边所在的直线方程;
(2)设M为直角三角形ABC外接圆的圆心,求圆M的方程;
(3)已知与AB平行的直线DE交x轴于点D,交y轴于点E(0,-7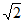 )。若P为圆M上任意一点,求三角形PDE面积的取值范围。
)。若P为圆M上任意一点,求三角形PDE面积的取值范围。
卷(Ⅱ)
一、过程性评价(考生不必作答):共10分
二、填空题:本大题共4小题,每小题4分,共16分
1. 圆(x-1)2+(y-3)2=5关于直线y=x对称的圆方程为_________。
2. 已知△ABC的三个顶点分别是A(0,3),B(4,2),C(2,1)。若直线l过点A,且将△ABC分割成面积相等的两部分,则直线l的方程是__________。
3. 如图,梯形ABCD中,AD∥BC,AD=AB=1,AD⊥AB,∠BCD=45°,将△ABD沿对角线BD折起,设折起后点A的位置为A’,且平面A’BD⊥平面BCD。则下列四个命题中正确的是__________。
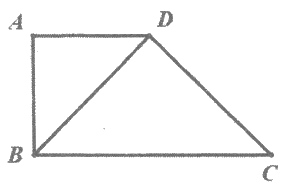
①A’D⊥BC ②三棱锥A’-BCD的体积为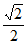
③CD⊥平面A’BD ④平面A’BD⊥平面A’DC
4. 在平面直角坐标系xOy中,A为直线l:y=2x上在第一象限内的点,B(5,0),以AB为直径的圆C与直线l交于另一点D。若∠DBA≥45°,则点A的横坐标的取值范围为__________。
三、解答题:本大题共2小题,共24分
5.(14分)在四棱锥P-ABCD中,平面ABCD⊥平面PCD,底面ABCD为直角梯形,AB∥CD,AD⊥DC,且AB=1,AD=DC=DP=2,∠PDC=120°。
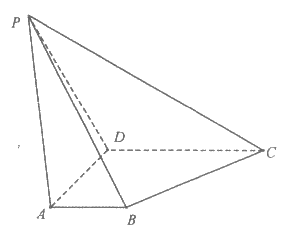
(1)求证:AD⊥平面PCD;
(2)线段BC上是否存在点F,使得平面PDF⊥平面PAC?如果存在,求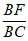 的值;如果不存在,说明理由;
的值;如果不存在,说明理由;
(3)若M是棱PA的中点,N为线段BC上任意一点,求证:MN与PC一定不平行。
6. (10分)设n∈N*,且n≥3。对1,2,…,n的一个排列i1 i2…in,如果当s<t时,有is>it,则称(is,it)是排列i1 i2…in的一个逆序,排列i1 i2…in的所有逆序的总个数称为其逆序数。例如:对1,2,3的一个排列231,只有两个逆序(2,1)(3,1),则排列231的逆序数为2。记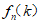 为1,2,…,n的所有排列中逆序数为k的全部排列的个数。
为1,2,…,n的所有排列中逆序数为k的全部排列的个数。
(1)求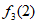 的值;
的值;
(2)判断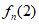 与
与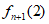 的大小,并说明理由;
的大小,并说明理由;
(3)求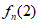 (n≥4)的表达式(用n表示)。
(n≥4)的表达式(用n表示)。
参考答案
卷(I)
1-10 BDBAC DCBCA
11 | 12 | 13 | 14 | 15 | 16 |
120° |
|
| -2 |
|
|
17. (1)因为OD为△ABC1的中位线,所以OD∥AB。
又AB∥A1B1,所以OD∥A1B1。
又OD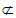 平面A1B1C1,
平面A1B1C1,
所以OD∥平面A1B1C1。
(2)因为AC⊥BC,CC1⊥BC,
所以BC⊥平面ACC1A1。
所以BC⊥AC1。
又因为AC1⊥A1C,所以AC1⊥平面A1BC。
所以平面AC1B⊥平面A1BC。
18. (1)建系.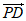 =(0,1,-1),
=(0,1,-1),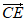 =
=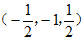 ,所以直线PD与CE所成角的余弦值
,所以直线PD与CE所成角的余弦值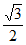 。
。
(2)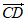 =(-1,0,0),平面ACE的法向量是
=(-1,0,0),平面ACE的法向量是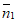 =(1,-1,-1),
=(1,-1,-1),
所以sin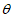 =
=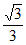 。
。
(3)平面ACP的法向量为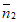 =
=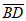 =(-1,1,0),
=(-1,1,0),
所以|cos<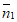 ,
,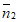 >|=
>|=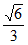 ,又由图可知,
,又由图可知,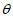 为锐角,所以cos
为锐角,所以cos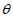 =
=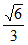 。
。
19. (1)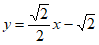 。
。
(2)M:(x+1)2+y2=9。
(3)DE:y=-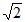 x-7
x-7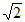 ,所以D(-7,0),所以|DE|=7
,所以D(-7,0),所以|DE|=7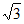 。
。
又h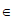 [d-r,d+r],即h∈[2
[d-r,d+r],即h∈[2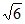 -3,2
-3,2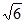 +3],
+3],
所以S∈[21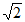 –
–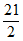
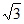 ,21
,21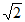 +
+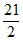
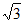 ]。
]。
卷(Ⅱ)
1 | 2 | 3 | 4 |
|
| ③④ |
|
5. (1)因为平面ABCD⊥平面PCD,
且AD⊥DC,
所以AD⊥平面PCD。
(2)存在。
从而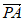 =(2,1,-
=(2,1,-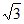 ),
),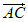 =(2,-2,0),
=(2,-2,0),
所以平面PAC的一个法向量是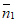 =(1,1,
=(1,1,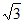 )。
)。
设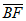 =
=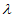
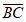 ,
,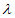 ∈[0,1],
∈[0,1],
则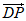 =(0,-1,
=(0,-1,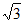 ),
),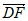 =(2-2
=(2-2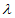 ,1+
,1+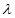 ,0)。
,0)。
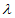 =1时,平面PDF的一个法向量
=1时,平面PDF的一个法向量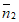 =(1,0,0),不成立;
=(1,0,0),不成立;
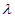 ≠1时,平面PDF的一个法向量
≠1时,平面PDF的一个法向量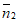 =
=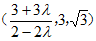 ,
,
所以由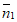 ·
·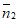 =0得,
=0得,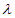 =
=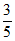 。
。
当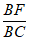 =
=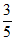 时,平面PDF⊥平面PAC。
时,平面PDF⊥平面PAC。
(3)建系。P(0,-1,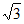 ),C(0,2,0);A(2,0,0),B(2,1,0)
),C(0,2,0);A(2,0,0),B(2,1,0)
所以M(1,-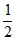 ,
,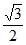 ),N(2-2
),N(2-2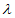 ,1+
,1+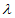 ,0)。
,0)。
从而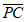 =(0,3,-
=(0,3,-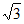 ),
),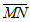 =(1-2
=(1-2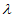 ,
,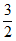 +
+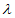 ,-
,-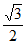 ),
),
则1-2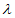 =0时,
=0时,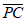 与
与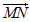 不平行;1-2
不平行;1-2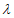 ≠0时,0≠2,
≠0时,0≠2,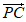 与
与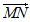 不平行。
不平行。
6. 解:(1)记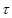 (abc)为排列abc的逆序数,对1,2,3的所有排列,有
(abc)为排列abc的逆序数,对1,2,3的所有排列,有
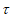 (123)=0,
(123)=0,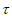 (132)=1,
(132)=1,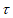 (213)=1,
(213)=1,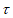 (231)=2,
(231)=2,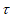 (312)=2,
(312)=2,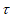 (321)=3,
(321)=3,
所以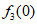 =1,
=1,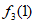 =
=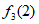 =2。
=2。
(2)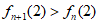 。
。
设i1 i2…in为12…n的一个逆序数为2的排列,则i1 i2…in(n+1)即为12…n(n+1)的一个逆序数为2的排列,且当i1 i2…in不同时,i1 i2…in(n+1)不同。故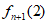 ≥
≥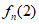 。
。
又123…(n+1)(n-1)n也是一个逆序数为2的排列,且它不能写成i1 i2…in(n+1)的形式,所以等号不成立,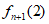 >
>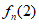 。
。
(3)对1,2,3,4的排列,利用已有的1,2,3的排列,将数字4添加进去,4在新排列中的位置只能是最后三个位置。因此,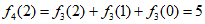 。
。
对一般的n(n≥4)的情形,逆序数为0的排列只有一个:12…n,所以fn(0)=1。
逆序数为1的排列只能是将排列12…n中的任意相邻两个数字调换位置得到的排列,所以fn(1)=n-1。
为计算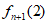 ,当1,2,…,n的排列及其逆序数确定后,将n+1添加进原排列,n+1在新排列中的位置只能是最后三个位置。
,当1,2,…,n的排列及其逆序数确定后,将n+1添加进原排列,n+1在新排列中的位置只能是最后三个位置。
因此,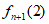 =
=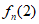 +
+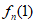 +
+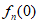 =
=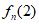 +n。
+n。
当n≥5时,
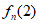 =[
=[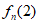 –
–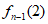 ]+[
]+[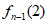 –
–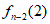 ]+…+[
]+…+[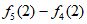 ]+
]+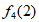
=(n-1)+(n-2)+…+4+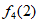 =
=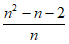 ,
,
因此,n≥5时,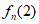 =
=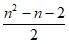 。
。