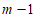本试卷A卷26道题,B卷4道题,共30道题,满分120分。考试时间100分钟。
A卷(满分100分)
一、选择题(每小题3分,共30分)
1. 2020年北京故宫迎来了600岁生日,系列展览与活动让故宫充分展示其深沉魅力,据不完全统计,今年”十一”双节期间故宫累计接待观众约为240000人次,将240000用科学记数法可表示为( )
A. 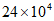 B.
B. 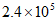 C.
C. 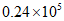 D.
D.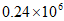
2. -5的倒数是( )
A. 5 B. -5 C. 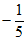 D.
D.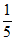
3. 下列各式结果为负数的是( )
A. 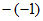 B.
B. 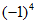 C.
C. 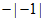 D.
D.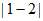
4. 下面计算正确的是( )
A. 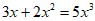 B.
B.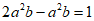
C. 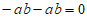 D.
D.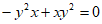
5. 下列各式去括号正确的是( )
A. 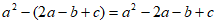 B.
B.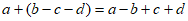
C. 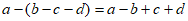 D.
D.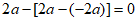
6. 有理数a、b、c在数轴上的对应点的位置如图所示,若a与c互为相反数,则a、b、c三个数中绝对值最大的数是( )
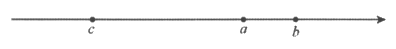
A. a B. b C. c D. 无法确定
7. 下列对使用四舍五入法得到的近似数描述正确的是( )
A. 近似数5.1万精确到十分位
B. 2.709的近似数是3
C. 0.154精确到十分位为0.1
D. 近似数1.31×105精确到千位
8. 如果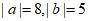 ,且
,且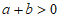 ,那么
,那么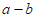 的值是( )
的值是( )
A. 3或13 B. 13或-13 C. 3或-3 D. -3或-13
9. 关于x的方程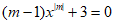 是一元一次方程,则m的值是( )
是一元一次方程,则m的值是( )
A. -1 B. 1 C. 1或-1 D. 2
10. 规定: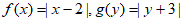 。
。
例如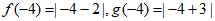 。
。
下列结论中:
①若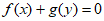 ,则
,则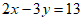 ;
;
②若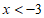 ,则
,则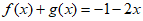 ;
;
③能使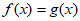 成立的x的值不存在;
成立的x的值不存在;
④式子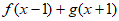 的最小值是7。
的最小值是7。
其中正确的所有结论是( )
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
二、填空题(每小题2分,共20分)
11. 如果水位升高3m时水位变化记作+3m,那么水位下降3m时水位变化记作____________m。
12. 比较大小: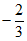 _______
_______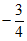 (填”>”、”<”或”=”)。
(填”>”、”<”或”=”)。
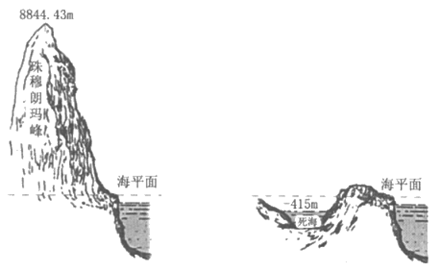
13. 如图所示,大陆上最高处是珠穆朗玛峰的峰顶,最低处位于亚洲西部名为死海的湖,两处高度相差是__________米。
14. 若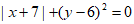 ,则
,则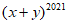 的值为__________。
的值为__________。
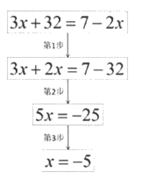
15. 下面的框图表示解方程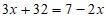 的流程,其中第3步的依据是____________。
的流程,其中第3步的依据是____________。
16. 如图,若开始输入的x的值为正数,最后输出的结果为51,则满足条件的x的值为____________。

17. 甲乙丙三个商店都在销售同一种排球,而且每个球的标价都是25元,但三个店的促销方式不一样:甲店的促销方式是每买十送二,乙店的促销方式是优惠16%,丙店的优惠方式是买球每满100元可返现金15元,学校准备买60个这种排球,你认为到________家商店买比较省钱,这时实际只需要付________元。
18. 已知数a,b,c在数轴上的对应点的位置如图所示,化简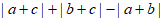 的结果为_______________。
的结果为_______________。
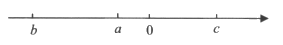
19. 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即”结绳计数”,如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是_________天。

20. 如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答。
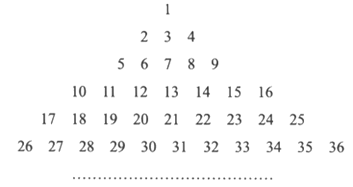
(1)表中第9行第7个数是__________________;
(2)2020是表中第________行第__________个数。
三、解答题(共50分)
21. 计算(每小题4分,共16分)
(1)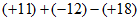 (2)
(2)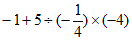
(3)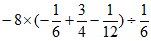 (4)
(4)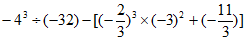
22. 化简(每小题4分,共8分)
(1)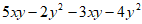 (2)
(2)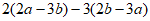
23. 解方程(每小题5分,共10分)
(1)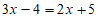 (2)
(2)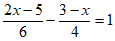
24. 先化简,再求值(本题5分)
求代数式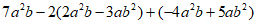 的值,其中
的值,其中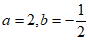 。
。
25. (本题5分)
对于任意四个有理数a,b,c,d,可以组成两个有理数对(a,b)与(c,d),我们规定: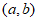 è
è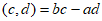 。例如:
。例如: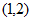 è
è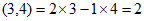 。
。
根据上述规定解决下列问题:
(1)有理数对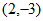 è
è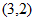 =___________;
=___________;
(2)若有理数对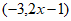 è
è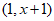 =7,则x=__________;
=7,则x=__________;
(3)当满足等式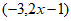 è
è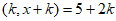 的x是整数时,求整数k的值。
的x是整数时,求整数k的值。
26. (本题6分)在数轴上,|a|表示数a的点到原点的距离,如果数轴上两个点A、B分别对应数a、b,那么A、B两点间的距离为:AB=|a-b|,这是绝对值的几何意义。已知如图,点A在数轴上对应的数为-3,点B对应的数为2。

(1)求线段AB的长;
(2)若点C在数轴上对应的数为x,且是方程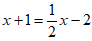 的解,在数轴上是否存在点M,使MA+MB=AB+BC?若存在,求出点M对应的数;若不存在,说明理由;
的解,在数轴上是否存在点M,使MA+MB=AB+BC?若存在,求出点M对应的数;若不存在,说明理由;
(3)若点N是数轴上在点A左侧的一点,线段BN的中点为点Q,点P为线段AN的三等分点且靠近于点N,当点N在点A左侧的数轴上运动时,请直接判断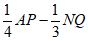 的值是否变化,如果不变请直接写出其值,如果变化请说明理由。
的值是否变化,如果不变请直接写出其值,如果变化请说明理由。

B卷(满分20分)
1. (本题4分)
(1)桌子上有5只杯口朝上的茶杯,每次翻转3只,经过m次翻转可使这5只杯子的杯口全部朝下,则m的最小值为__________。
(2)桌子上有11只杯口朝上的茶杯,每次翻转3只,经过n次翻转可使这11只杯子的杯口全部朝下,则n的最小值为___________。
2. (本题6分)如下表,从左向右依次在每个小格子中都填入一个有理数,使得其中任意四个相邻小格子中所填数之和都等于15。已知第3个数为7,第5个数为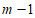 ,第16个数为2,第78个数为
,第16个数为2,第78个数为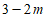 ,则m的值为________,第2021个数为_________。
,则m的值为________,第2021个数为_________。
7 |
| … |
3. (本题4分)天坛中的数学一瞥
天坛始建于明朝永乐十八年(1420年),明、清两代是帝王祭祀皇天、祈五谷丰登之场所,中和韶乐在中国古代的发生、发展、沉寂、经历了历代传承,随着对中国传统文化重新认识,中和韶乐逐渐复苏,自从2004年9月天坛神乐署修复完成,中和韶乐又一次展现在世人面前,中和韶乐主要是宫、商、角、徵、羽五声音阶的运用,在确定这五音的时候,中国古代最初由三分损益计算而来,从最初的一个音三分损一而得到第二个音,由第二个音三分益一得到第三个音,如此计算,得到宫商角徵羽五声音阶。例如:假设能发出第一个基准音的乐器的长度为81,那么能发出第二个基准音的乐器的长度为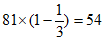 ,能发出第三个基准音的乐器的长度为
,能发出第三个基准音的乐器的长度为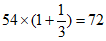 …,(也就是依次先减少三分之一,后增加三分之一)。那么第五个基准音的乐器的长度为_____________。假设能发出第一个基准音的乐器的长度为a,那么能发出第四个基准音的乐器的长度是32,则a的值是___________。
…,(也就是依次先减少三分之一,后增加三分之一)。那么第五个基准音的乐器的长度为_____________。假设能发出第一个基准音的乐器的长度为a,那么能发出第四个基准音的乐器的长度是32,则a的值是___________。

4. (本题6分)阅读材料:
你知道”二维码”吗?它是一种编码,通过表示1和0的黑白小方块排列成图案传递信息,二维码广泛应用于我们生活,”扫一扫”成为人们的习惯动作。
你知道二维码究竟是怎样生成的吗?你想亲自制作一个二维码吗?首先来了解一个定义:定义符号”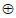 “表示一种运算叫做”异或”运算,即当
“表示一种运算叫做”异或”运算,即当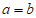 时,
时,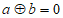 ;当
;当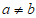 时,
时,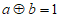 。
。
下面就让我们试着为”BHSF”制作一个二维码吧!
【步骤一】
查表可得字母”B”的八位二进制编码为01000010,”H”为01001000,”S”为01010011,”F”为01000110。
【步骤二】
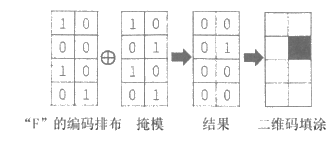
将每个字母的编码按照一定的顺序排布在方格内,例如字母”S”的编码排布如下图第一个表格,然后将编码排布与事先排布好0与1的表格(称为掩模)进行”方格一一对应”的”异或”运算(如下图第三个表格),并将结果中1的位置填涂黑色,0的位置填涂白色(如下图第四个表格)。
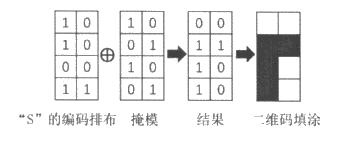
解决问题:
(1)请根据上面的定义将表格补充完整。
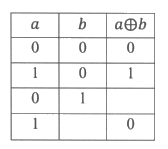
(2)仿照上面【步骤二】,完成”F”的编码排布、运算及二维码填涂。
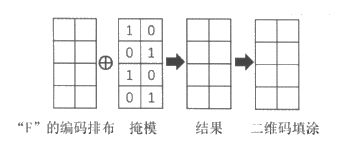
“BHSF”二维码的其余部分已生成,你可以将获得的结果填涂在对应的空白位置,一个完整的二维码就大功告成啦,试着扫一扫它吧!

【试题答案】
A卷(满分100分)
一、选择题
1-10 BCCDC BDAAB
二、填空题
11. -3 12. > 13. 9259.43
14. -1 15. 等式的性质2 16.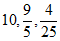
17. 甲,1250 18. 2a 19. 510
20. (1)71 (2)第45行第84个数
三、解答题
21. (1)-19 (2)79
(3)-24 (4)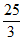
22.(1)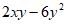 (2)
(2)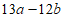
23.(1)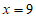 (2)
(2)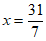
24. 化简结果: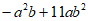 值:
值: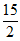
25. (1)-13 (2)1 (3)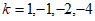
26. (1)5 (2)-7或者6 (3)不变。值为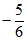
B卷(满分20分)
1. (1)3(2)5
2. -4,-5
3. 64. 54
4.(1)
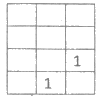
(2)