本试卷共26道题,满分100分。考试时间120分钟。
一、选择题(每题2分,共16分)
下面各题均有四个选项,其中只有一个是符合题意的。
1. 二次函数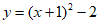 的最小值是( )
的最小值是( )
A. 1 B. -1 C. 2 D. -2
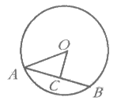
2. 如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的大小为( )
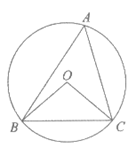
A. 40° B. 50° C. 80° D. 100°
3. 若将抛物线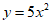 先向右平移2个单位,再向上平移1个单位,则得到的新抛物线的表达式为( )
先向右平移2个单位,再向上平移1个单位,则得到的新抛物线的表达式为( )
A. 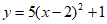 B.
B.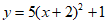
C. 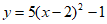 D.
D.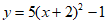
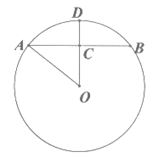
4. 如图,AB为⊙O的弦,点C为AB的中点,AB=8,OC=3,则⊙O的半径长为( )
A. 4 B. 5 C. 6 D. 7
5. 已知A(-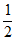 ,y1),B(1,y2),C(4,y3)三点都在二次函数
,y1),B(1,y2),C(4,y3)三点都在二次函数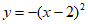 的图象上,则y1,y2,y3的大小关系为( )
的图象上,则y1,y2,y3的大小关系为( )
A. y1< y2< y3 B. y1< y3< y2 C. y3< y1< y2 D. y3< y2< y1
6. 如图,⊙O中直径AB⊥DG于点C,点D是弧EB的中点,CD与BE交于点F。下列结论①∠A=∠E,②∠ADB=90°,③FB=FD中正确的个数为( )
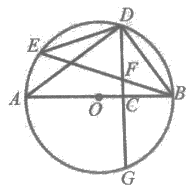
A. 0 B. 1 C. 2 D. 3
7. 已知抛物线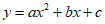 (a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x | … | -2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | -4 | 0 | 2 | 2 | 0 | -4 | … |
下列结论:
①抛物线开口向下; ②当-1<x<2时,y>0;
③抛物线的对称轴是直线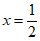 ④函数
④函数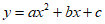 (a≠0)的最大值为2。
(a≠0)的最大值为2。
其中所有正确的结论为( )
A. ①②③ B. ①③ C. ①③④ D. ①②③④
8. 如图,在平面直角坐标系xOy中,以(3,0)为圆心作⊙P,⊙P与x轴交于A、B,与y轴交于点C(0,2),Q为⊙P上不同于A、B的任意一点,连接QA、QB,过P点分别作PE⊥QA于E,PF⊥QB于F。设点Q的横坐标为x,PE2+PF2=y。当Q点在⊙P上顺时针从点A运动到点B的过程中,下列图象中能表示y与x的函数关系的部分图象是( )
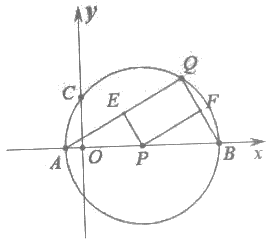
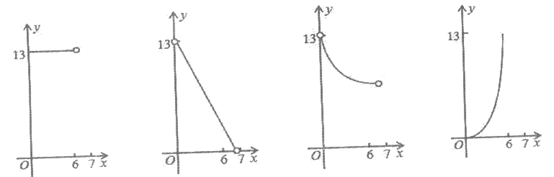
A B C D
二、填空题(本题共16分,每小题2分)
9. 若抛物线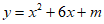 与x轴只有一个公共点,则m的值为_________。
与x轴只有一个公共点,则m的值为_________。
10. 如图,A,B,C是⊙O上的三个点,如果∠AOB=140°,那么∠ACB的度数为_________。
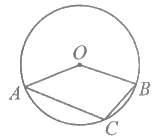
11. 若点(1,5),(5,5)是抛物线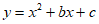 (a≠0)上的两个点,则b=_________。
(a≠0)上的两个点,则b=_________。
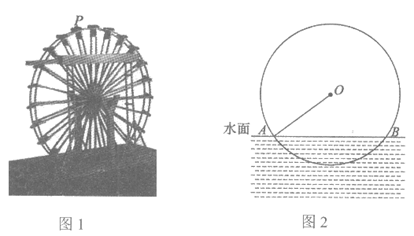
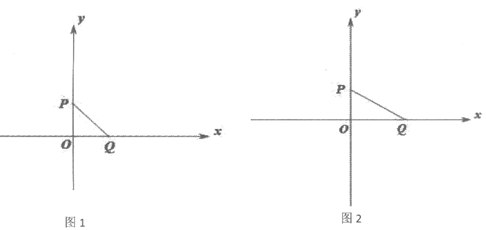
12. 筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点P表示筒车的一个盛水桶。如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5 m为半径的圆,且圆心在水面上方。若圆被水面截得的弦AB长为8m,则筒车工作时,盛水桶在水面以下的最大深度为___________m。
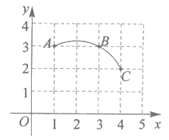
13. 如图,在平面直角坐标系中,点A,B,C都在格点上,过A,B,C三点作一圆弧,则圆心的坐标是_________。
14. 已知关于x的二次函数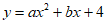 的图象如下图所示,则关于x的方程
的图象如下图所示,则关于x的方程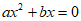 的根为_________。
的根为_________。
15. 元元同学在数学课上遇到这样一个问题:
如图1,在平面直角坐标系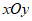 中,⊙A经过坐标原点O,并与两坐标轴分别交于B、C两点,点B的坐标为(2,0),点D在⊙A上,且∠ODB=30°,求⊙A的半径。
中,⊙A经过坐标原点O,并与两坐标轴分别交于B、C两点,点B的坐标为(2,0),点D在⊙A上,且∠ODB=30°,求⊙A的半径。
元元的做法如下,请你帮忙补全解题过程。
解:如图2,连接BC。
∵∠BOC=90°,
∴BC是⊙A的直径。(依据是________________________________)
∵∠ODB=30°,
∴∠OCB=∠ODB=30°。(依据是_______________________________)
∴OB=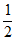 BC。
BC。
∵OB=2,
∴BC=4。即⊙A的半径为2。
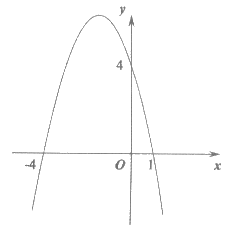
16. 抛物线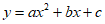 经过点(1,0),且对称轴为直线x=-1,其部分图象如图所示。对于此抛物线有如下四个结论:
经过点(1,0),且对称轴为直线x=-1,其部分图象如图所示。对于此抛物线有如下四个结论:
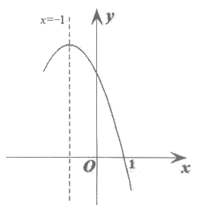
①abc<0;②2a+b=0;③4a-2b+c>0;
④若m>n>0,则x=m-1时的函数值小于x=n-1时的函数值。其中正确结论的序号是_________。
三、解答题(本题共68分,第17题每小题5分共10分,第18、19、21、22、24题每题6分,第20、23、25、26题每题7分)
17. 解关于x的方程。
(1)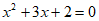 ; (2)
; (2)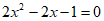 。
。
18. 已知抛物线的顶点为(-2,2),且过坐标原点,求抛物线的解析式。
19. 如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,连接OA。若AB=4,CD=1,求⊙O半径的长。
20. 已知抛物线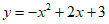 ,回答下列问题:
,回答下列问题:
(1)画出该函数图象(要求列表、2B铅笔画图);
x | … | … | |||||
y | … | … |
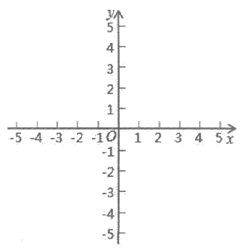
(2)当-3<x<3时,y的取值范围是__________。
21. 如图,△ABC中AB=AC,以AB为直径作⊙O交BC于点D,DE⊥AC于点E。
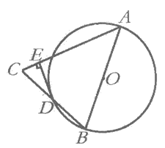
求证:(1)BD=DC;
(2)DE是⊙O的切线。
22. 学生会要组织”四中杯”篮球赛,赛制为单循环形式(每两队之间都赛一场)。
(1)如果有4支球队参加比赛,那么共进行_________场比赛;
(2)如果全校一共进行36场比赛,那么有多少支球队参加比赛?
23. 在画函数图象时,我们常常通过描点、平移或翻折的方法。某班”数学兴趣小组”根据学到的函数知识探究函数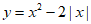 的图象与性质,并利用函数图象解决问题。探究过程如下,请补充完整。
的图象与性质,并利用函数图象解决问题。探究过程如下,请补充完整。
(1)函数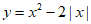 的自变量x的取值范围是_________。
的自变量x的取值范围是_________。
(2)化简:当x>0时函数y=_________,当x<0时函数y=_________。
(3)根据上题,在如图所示的平面直角坐标系中描点,画出该函数的图象,并写出该函数的一条性质:
__________________________________________________。
(4)若直线y=k与该函数只有两个公共点,根据图象判断k的取值范围为________。
24. 在平面直角坐标系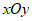 中,抛物线
中,抛物线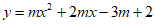 。
。
(1)求抛物线的对称轴;
(2)过点P(0,2)作与x轴平行的直线,交抛物线于点M,N。求点M,N的坐标;
(3)横、纵坐标都是整数的点叫做整点。如果抛物线和线段MN围成的封闭区域内(不包括边界)恰有3个整点,求m的取值范围。
25. (1)已知等边三角形ABC,请作出△ABC的外接圆⊙O。在⊙O上任取一点P(异于A、B、C三点),连结PA、PB、PC。
①依题意补全图形,要求尺规作图,不写作法,保留作图痕迹;
②请判断PA、PB、PC的关系,并给出证明。
(2)已知⊙O,请作出⊙O的内接等腰直角三角形ABC,∠C=90°。在⊙O上任取一点P(异于A、B、C三点),连结PA、PB、PC。
①依题意补全图形,要求尺规作图,不写作法,保留作图痕迹;
②请判断PA、PB、PC的关系,并给出证明。
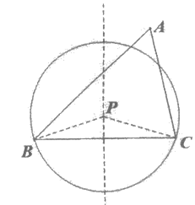
26. 在平面直角坐标系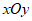 中,对于△ABC,点P在BC边的垂直平分线上,若以点P为圆心,PB为半径的⊙P与△ABC三条边的公共点个数之和不小于3,则称点P为△ABC关于边BC的”Math点”。
中,对于△ABC,点P在BC边的垂直平分线上,若以点P为圆心,PB为半径的⊙P与△ABC三条边的公共点个数之和不小于3,则称点P为△ABC关于边BC的”Math点”。
下图所示,点P即为△ABC关于边BC的”Math点”已知点P(0,4),Q(a,0)
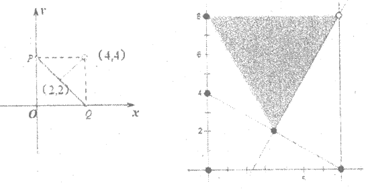
(1)如图1,a=4,在点A(1,0)、B(2,2)、C(2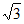 ,2
,2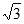 )、D(5,5)中,△POQ关于边PQ的”Math点”为___________。
)、D(5,5)中,△POQ关于边PQ的”Math点”为___________。
(2)如图2,a=4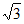 ,
,
①已知D(0,8),点E为△POQ关于边PQ的”Math点”,请直接写出线段DE的长度的取值范围;
②将△POQ绕原点O旋转一周,直线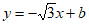 交x轴、y轴于点M、N,若线段MN上存在△POQ关于边PQ的”Math点”,求b的取值范围。
交x轴、y轴于点M、N,若线段MN上存在△POQ关于边PQ的”Math点”,求b的取值范围。
参考答案
一、选择题
l. D 2. B 3. A 4. B 5. B 6. D 7. A 8. A
二、填空题
9. 9 10. 110 11. -6 12. 2 13. (2,1) 14. -3,0
15. 90°的圆周角所对的弦是直径,同弧所对的圆周角相等。
16、③④
三、解答题
17. (1)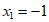 ,
,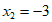 ;(2)
;(2)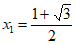 ,
,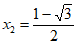 。
。
18. 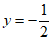 (x+2)2+2或
(x+2)2+2或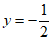 x2-2x。
x2-2x。
19. ⊙O半径的长为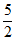 。
。
20. (1)图略
(2)-12<y≤4。
21. 证明略。
22. (1)6;
(2)解:设有x支球队参加比赛。
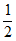 x(x-1)=36
x(x-1)=36
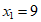 ,
,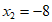 。
。
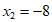 不合题意,舍去。
不合题意,舍去。
答:有9支球队参加比赛。
23. (1)函数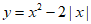 的自变量x的取值范围是全体实数。
的自变量x的取值范围是全体实数。
(2)当x>0时函数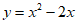 ,当x<0时函数
,当x<0时函数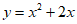 。
。
(3)图象略,写出该函数的一条性质;当x>1时,y随x增大而增大。(答案不唯一)
(4)若直线y=k与该函数只有两个公共点,根据图象判断k的取值范围为k=-1或k>0。
24. 在平面直角坐标系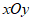 中,抛物线
中,抛物线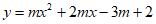 。
。
(1)求抛物线的对称轴;
(2)过点P(0,2)作与x轴平行的直线,交抛物线于点M,N。求点M,N的坐标;
(3)横、纵坐标都是整数的点叫做整点。如果抛物线和线段MN围成的封闭区域内(不包括边界)恰有3个整点,求出m的取值范围。
解:(1)对称轴为直线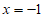 ;
;
(2)M(-3,2);N(1,2)
(3)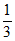 <m≤
<m≤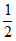 或
或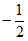 ≤m<
≤m<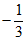
25. (1)①如下图1、图2。
②由图1,由∠APB=∠ACB=60°,做等边三角形△APE。
可得△APC≌△AEB,可得BP=AP+PC。
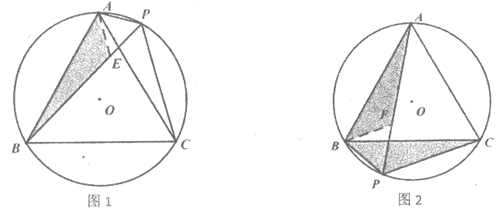
由图2,同理可得AP=BP+PC。
(2)①如下图3、图4;
②请判断PA、PB、PC的关系,并给出证明。
由图3,由∠APB=∠ACB=45°,做等腰直角三角形△APE。
可得△CAK≌△CBP,可得AP-BP=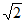 PC。
PC。
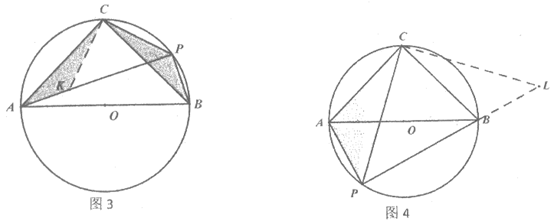
由图4,同理可得AP+BP=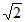 PC。
PC。
26. 答案:
(1)B、C
(2)6≤DE≤4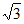
(3)4≤b<8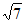 或-8
或-8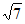 <b≤-4。
<b≤-4。