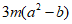本试卷共29道小题,满分120分。考试时间100分钟。
一、选择题(每小题3分,共30分)
1. 下列轴对称图形中,有4条对称轴的图形是( )

A B C D
2. 下列运算正确的是( )
A. 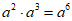 B.
B.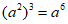
C. 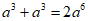 D.
D.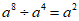
3. 下列变形属于因式分解的是( )
A. 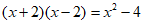 B.
B.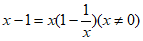
C. 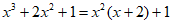 D.
D.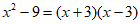
4. 在平面直角坐标系上,点A关于直线x=l对称的点为B(-2,4),则点A的坐标为( )
A. (4,4) B. (-2,-2) C. (2,4) D. (3,4)
5. 电子文件的大小常用B,KB,MB,GB等作为单位,其中1GB=210MB,1MB=210KB,1KB=210B。某视频文件的大小约为1GB,1GB等于( )
A. 230B B. 830B C. 8×1010B D. 2×1030B
6. 已知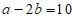 ,
,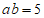 ,则
,则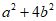 的值是( )
的值是( )
A. 110 B. 120 C. 125 D. 130
7. 如图所示,图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空余的部分的面积是( )
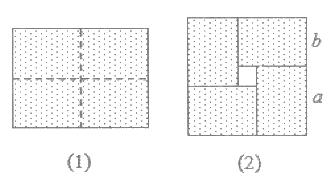
A. ab B. (a+b)2 C. (a–b)2 D. a2–b2
8. 如图所示,三角形纸片被正方形纸板遮住了一部分,小明根据所学知识画出了一个与该三角形完全重合的三角形,那么这两个三角形完全重合的依据是( )

A. SSS B. SAS C. AAS D. ASA
9. 我们利用尺规作图可以作一个角(∠A’O’B’)等于已知角(∠AOB),如下所示:
(1)作射线O’A’;
(2)以O为圆心,任意长为半径作弧,交OA于C,交OB于D;
(3)以O’为圆心,OC为半径作弧,交O’A’于C’;
(4)以C’为圆心,OC为半径作弧,交前面的弧于D’;
(5)连接O’D’作射线O’B’,则∠A’O’B’就是所求作的角。
以上作法中,错误的一步是( )
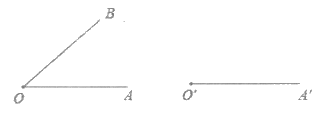
A. (2) B. (3) C. (4) D. (5)
10. △BDE和△FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内。若求五边形DECHF的周长,则只需知道( )。
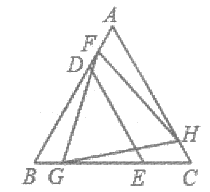
A. △ABC的周长 B. △AFH的周长
C. 四边形FBGH的周长 D. 四边形ADEC的周长
二、填空题(每小题2分,共16分)
11. 分解因式:3ma2-3mb=___________。
12. 在正方形网格中,∠AOB的位置如图所示,则点P、Q、M、N中在∠AOB的平分线上是_________点。
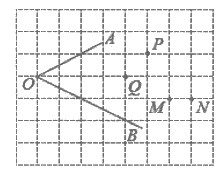
13. 已知3x+2y-2=0,则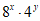 =__________。
=__________。
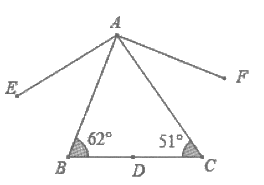
14. 如图,△ABC中,D点在BC上,将D点分别以AB、AC为对称轴,画出对称点E、F,并连接AE、AF。根据图中标示的角度,则∠EAF的度数为_________。
15. 已知关于x的代数式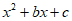 ,设代数式的值为y,则y=
,设代数式的值为y,则y=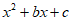 。下表中列出了当x分别取…,-1,0,1,2,3,4,5,…,m,m+1…时对应的y值。
。下表中列出了当x分别取…,-1,0,1,2,3,4,5,…,m,m+1…时对应的y值。
x | … | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … | m | m+1 | … |
Y | … | 10 | 5 | 2 | 1 | 2 | 5 | n | … | p | q | … |
(1)表中n的值为__________;
(2)当x=__________时,y有最小值,最小值是__________;
(3)p_____q。(填<,>,=)
16. 已知等腰三角形的一个外角的度数为108°,则顶角的度数为__________。
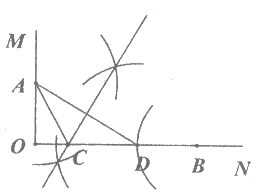
17. 已知锐角∠AOB,如图,
(1)在射线OA上取一点C,以点O为圆心,OC长为半径作弧MN,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,两弧交于点P,连接CP,DP;
(3)作射线OP交CD于点Q。
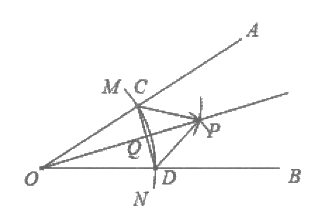
根据以上作图过程及所作图形,下列结论中正确的是_______________。
①CP∥OB ②CP=2QC ③∠AOP=∠BOP ④CD⊥OP
18. 如图,已知每个小方格的边长为1,A,B两点都在小方格的顶点上(即为格点),请在图中找一个格点C,使△ABC为等腰三角形,则这样的格点C有__________个。
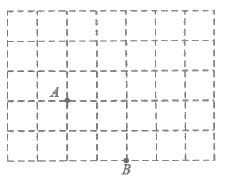
三、解答题
19. (每小题4分)分解因式:
(1)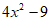 ; (2)
; (2)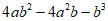 。
。
20. (每小题4分)计算:
(1)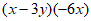 (2)
(2)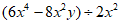 ;
;
(3) 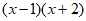 ; (4)
; (4)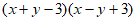 。
。
21. (5分)先化简,再求值: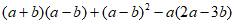 ,其中
,其中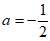 ,b=1。
,b=1。
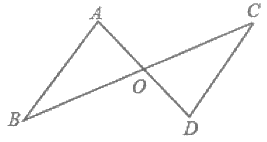
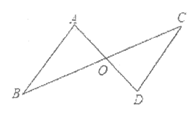
22. (6分)已知:如图,AB∥CD,AD与BC相交于点O,且OA=OD,
求证:OB=OC。
23. (6分)小宇遇到了这样一个问题:
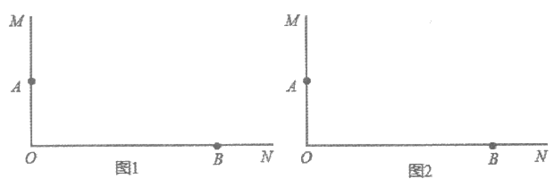
已知:如图,∠MON=90°,点A,B分别在射线OM,ON上,且满足OB>2OA。
求作:线段OB上的一点C,使△AOC的周长等于线段OB的长。
以下是小宇分析和求解的过程,请补充完整:
首先画草图进行分析,如图1所示,若符合题意的点C已经找到,即△AOC的周长等于OB的长,那么由OA+OC+AC=OB=OC+BC,可以得到OA+AC=__________。
对于这个式子,可以考虑用截长的办法,在BC上取一点D,使得BD=AO,那么就可以得到CA=___________。
若连接AD,由____________________________________ (填推理的依据),可知点C在线段AD的垂直平分线上,于是问题的解法就找到了。
请根据小宇的分析,在图2中完成作图(尺规作图,不写作法,保留作图痕迹)。
24. (6分)阅读材料。
小明遇到这样一个问题:求计算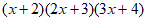 所得多项式的一次项系数。
所得多项式的一次项系数。
小明想通过计算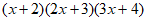 所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法。
所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法。
他决定从简单情况开始,先找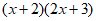 所得多项式中的一次项系数,通过观察发现:
所得多项式中的一次项系数,通过观察发现:
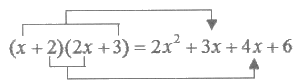
也就是说,只需用x+2中的一次项系数1乘以2x+3中的常数项3,再用x+2中的常数项2乘以2x+3中的一次项系数2,两个积相加1×3+2×2=7,即可得到一次项系数。
延续上面的方法,求计算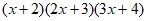 所得多项式的一次项系数,可以先用x+2的一次项系数1,2x+3的常数项3,3x+4的常数项4,相乘得到12;再用2x+3的一次项系数2,x+2的常数项2,3x+4的常数项4,相乘得到16;然后用3x+4的一次项系数3,x+2的常数项2,2x+3的常数项3,相乘得到18。最后将12,16,18相加,得到的一次项系数为46。
所得多项式的一次项系数,可以先用x+2的一次项系数1,2x+3的常数项3,3x+4的常数项4,相乘得到12;再用2x+3的一次项系数2,x+2的常数项2,3x+4的常数项4,相乘得到16;然后用3x+4的一次项系数3,x+2的常数项2,2x+3的常数项3,相乘得到18。最后将12,16,18相加,得到的一次项系数为46。
参考小明思考问题的方法,解决下列问题:
(1)计算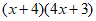 所得多项式的一次项系数为_____________。
所得多项式的一次项系数为_____________。
(2)计算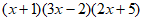 所得多项式的一次项系数为_____________。
所得多项式的一次项系数为_____________。
(3)若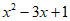 是
是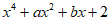 的一个因式,求a,b的值。
的一个因式,求a,b的值。
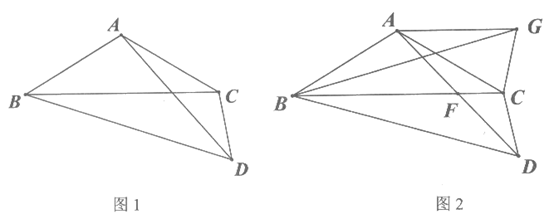
25. (7分)如图1,点D是等腰三角形ABC外一点,AB=AC,∠BDC=2∠ABC,过点A作AE⊥BD于点E,
(1)依据题意,补全图形。
(2)求证:DE=BE+CD。
(3)如图2,AD与BC交于点F,当F是AD的中点时,翻折△BCD得到△BCG,连接AG,求证:A,G两点到直线BC的距离相等。
附加题
1. (4分)若k为正奇数,则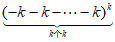 =____________;
=____________;
若k为正偶数,则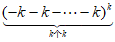 =____________。
=____________。
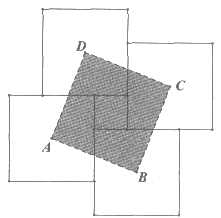
2. (3分)用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案,每块大正方形地砖面积为a,小正方形地砖面积为b,依次连接四块大正方形地砖的中心得到正方形ABCD。则正方形ABCD的面积为____________。(用含a,b的代数式表示)。
3. (8分)小明同学研究如下问题:
从1,2,3,…,n(n为整数,且n≥3)这n个整数中任取a(1<a<n)个整数,这a个整数之和共有多少种不同的结果?
他采取一般问题特殊化的策略,先从最简单的情形入手,再逐次递进,从中找出解决问题的方法。他进行了如下几个探究:
探究一:
(1)从1,2,3这3个整数中任取2个整数,这2个整数之和共有多少种不同的结果?
所取的2个整数 | 1,2 | 1,3 | 2,3 |
2个整数之和 | 3 | 4 | 5 |
表①
如表①,所取的2个整数之和可以为3,4,5,也就是从3到5的连续整数,其中最小是3,最大是5,所以共有3种不同的结果。
(2)从l,2,3,4这4个整数中任取2个整数,这2个整数之和共有多少种不同的结果?
所取的2个整数 | 1,2 | 1,3 | 1,4 | 2,3 | 2,4 | 3,4 |
2个整数之和 | 3 | 4 | 5 | 5 | 6 | 7 |
表②
如表②,所取的2个整数之和可以为3,4,5,6,7,也就是从3到7的连续整数,其中最小是3,最大是7,所以共有5种不同的结果。
(3)从1,2,3,4,5这5个整数中任取2个整数,这2个整数之和共有________种不同的结果。
(4)从1,2,3,…,n(n为整数,且n≥3)这n个整数中任取2个整数,这2个整数之和共有__________种不同的结果。
探究二:
(1)从1,2,3,4这4个整数中任取3个整数,这3个整数之和共有_________种不同的结果。
(2)从1,2,3,…,n(n为整数,且n≥4)这n个整数中任取3个整数,这3个整数之和共有_________种不同的结果。
探究三:
从l,2,3,…,n,(n为整数,且n≥5这n个整数中任取4个整数,这4个整数之和共有_________种不同的结果。
归纳结论:
从1,2,3,…,n(n为整数,且n≥3这n个整数中任取a(1<a<n)个整数,这a个整数之和共有_________种不同的结果。
拓展延伸:
从1,2,3,…,36这36个整数中任取_________个整数,使得取出的这些整数之和共有204种不同的结果?(写出解答过程)
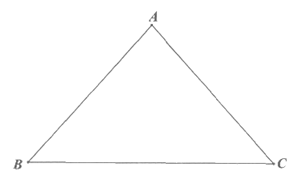
4. (5分)如图,△ABC中,AB=AC,60°<∠BAC<120°,将线段AB绕点A逆时针旋转60°得到点D,点E与点D关于直线BC对称,连接CD,CE,DE。
(1)依题意补全图形;
(2)判断△CDE的形状,并证明;
(3)请问在直线CE上是否存在点P,使得PB-PA=CD成立?若存在,请用文字描述出点P的准确位置,并画图证明;若不存在,请说明理由。
参考答案
一、选择题
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
D | B | D | A | A | C | C | D | C | A |
二、填空题
11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Q | 4 | 134° | 10,2,1,< | 72°或36° | ②③④ | 8 |
三、解答题
19. (1)原式=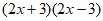 ;
;
(2)原式=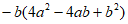
=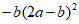
20. (1)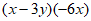
=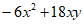 ;
;
(2)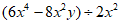
=3x2-4y;
(3)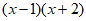
=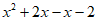
=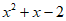 ;
;
(4)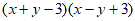
=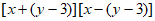
=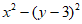
=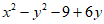
21. 解:原式=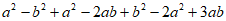
=ab
当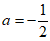 ,b=1时,原式=
,b=1时,原式=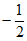 。
。
22. 证明:
∵AB∥CD,
∴∠B=∠C,
在△AOB和△DOC中,
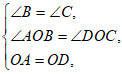
∴△AOB≌△DOC(AAS),
∴OB=OC。
23. 解:如图,△AOC即为所求。
故答案为:BC,DC,与线段两个端点距离相等的点在这条线段的垂直平分线上。
24. 解:(1)19;(2)1;
(3)由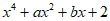 中4次项系数为1、常数项为2可设另一个因式为
中4次项系数为1、常数项为2可设另一个因式为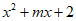 ,
,
则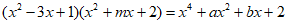 ,
,
∴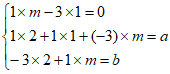 ,解得:
,解得: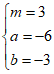 。
。
25. (1)如下图。
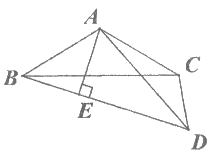
(2)如图,延长DB到点F,使BF=CD,连接AF,
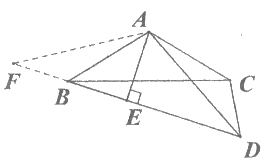
∵AB=AC,
∴∠ABC=∠BCA。
∵在△ABC中,∠ABC+∠BCA+∠BAC=180°,
∴2∠ABC+∠BAC=180°。
∵∠BDC=2∠ABC,
∴∠BDC+∠BAC=180°。
∵在四边形ABDC中,∠BDC+∠BAC+∠ABD+∠ACD=360°。
∴∠ABD+∠ACD=180°。
∵∠ABD+∠ABF=180°,
∴∠ACD=∠ABF。
在△ABF和△ACD,
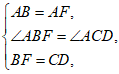
∴△ABF≌△ACD(SAS)。
∴AF=AD。
∵AE⊥FD,
∴FE=ED。
∵BE+BF=FE,BF=CD,
∴BE+CD=DE。
(3)如图,过点A做AH⊥BC于点H,连接GD交直线BC于点I,连GF。
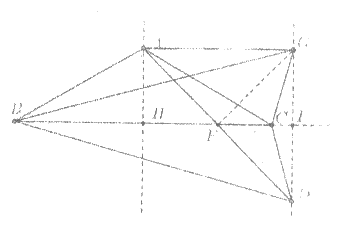
∵点G与点D关于直线BC对称,
∴直线BC是线段GD的垂直平分线。
∴∠DIF=∠GIF=90°,GI=DI。
∵AH⊥BC,
∴∠AHF=90°。
在△AHF和△DIF中,
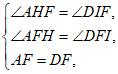
∴△AHF≌△DIF(AAS)。
∴AH=DI。
∵DI=GI。
∴AH=GI。
即点A与点G到直线BC的距离相等。