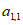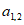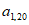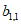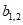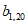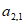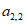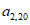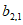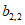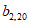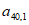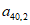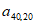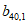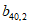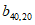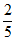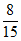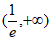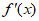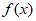本试卷共150分。考试时长120分钟。
第Ⅰ卷(选择题 共40分)
一、选择题:本大题共10小题,每小题4分,共40分,在每小题列出的四个选项中,选出符合题目要求的一项。
1. 设全集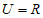 ,集合
,集合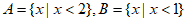 ,则集合
,则集合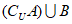 =
=
A. 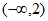 B.
B. 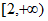 C.
C. 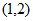 D.
D.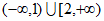
2. 设复数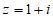 ,则
,则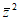 =
=
A. 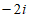 B.
B. 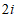 C.
C. 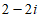 D.
D.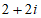
3. 焦点在x轴的正半轴上,且焦点到准线的距离为4的抛物线的标准方程是
A. 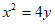 B.
B. 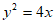 C.
C. 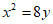 D.
D.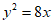
4. 在锐角△ABC中,若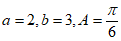 ,则cosB=
,则cosB=
A. 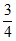 B.
B. 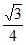 C.
C. 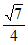 D.
D.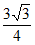
5. 函数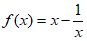 是
是
A. 奇函数,且值域为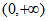 B. 奇函数,且值域为R
B. 奇函数,且值域为R
C. 偶函数,且值域为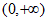 D. 偶函数,且值域为R
D. 偶函数,且值域为R
6. 圆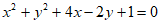 截x轴所得弦的长度等于
截x轴所得弦的长度等于
A. 2 B. 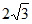 C.
C. 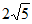 D. 4
D. 4
7. 设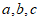 为非零实数,且
为非零实数,且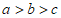 ,则
,则
A. 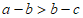 B.
B.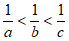
C. 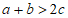 D. 以上三个选项都不对
D. 以上三个选项都不对
8. 设向量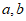 满足
满足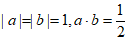 ,则
,则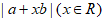 的最小值为
的最小值为
A. 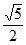 B.
B. 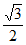 C. 1 D.
C. 1 D.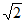
9. 设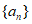 为等比数列,则”对于任意的
为等比数列,则”对于任意的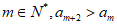 “是”
“是”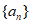 为递增数列”的
为递增数列”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
10. 佩香囊是端午节传统习俗之一,香囊内通常填充一些中草药,有清香、驱虫、开窍的功效,因地方习俗的差异,香囊常用丝布做成各种不同的形状,形形色色,玲珑夺目。
图1的平行四边形ABCD由六个正三角形构成,将它沿虚线折起来,可得图2所示的六面体形状的香囊,那么在图2这个六面体中,棱AB与CD所在直线的位置关系为
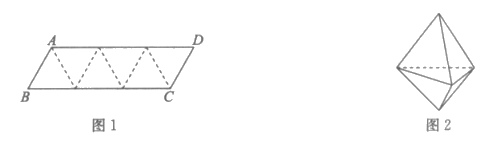
A. 平行 B. 相交 C. 异面且垂直 D. 异面且不垂直
第Ⅱ卷(非选择题 共110分)
二、填空题:本大题共5小题,每小题5分,共25分。
11. 在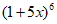 的展开式中,x的系数为____________。
的展开式中,x的系数为____________。
12. 在等差数列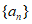 中,若
中,若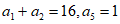 ,则
,则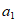 =__________;使得数列
=__________;使得数列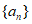 前n项的和
前n项的和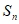 取到最大值的n=__________。
取到最大值的n=__________。
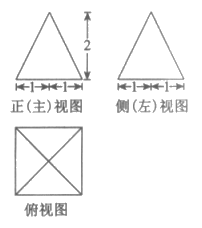
13. 某几何体的三视图如图所示,则该几何体的表面积为_________。
14. 能说明”若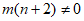 ,则方程
,则方程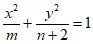 表示的曲线为椭圆或双曲线”是错误的一组
表示的曲线为椭圆或双曲线”是错误的一组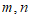 的值是___________。
的值是___________。
15. 已知函数f(x))的定义域为R,满足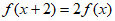 ,且当
,且当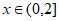 时,
时,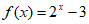 。有以下三个结论:
。有以下三个结论:
①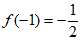
②当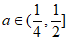 时,方程
时,方程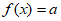 在区间
在区间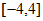 上有三个不同的实根;
上有三个不同的实根;
③函数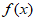 有无穷多个零点,且存在一个零点
有无穷多个零点,且存在一个零点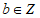 。
。
其中,所有正确结论的序号是_________。
三、解答题:本大题共6小题,共85分,解答应写出必要的文字说明、证明过程或演算步骤。
16. (本小题满分14分)
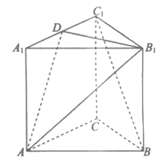
如图,在三棱柱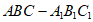 中,
中,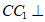 底面ABC,AC⊥BC,D是
底面ABC,AC⊥BC,D是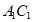 的中点,且
的中点,且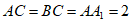 。
。
(Ⅰ)求证: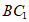 ∥平面
∥平面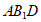 ;
;
(Ⅱ)求直线BC与平面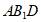 所成角的正弦值。
所成角的正弦值。
17. (本小题满分14分)
已知函数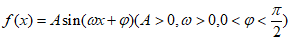 同时满足下列四个条件中的三个:
同时满足下列四个条件中的三个:
①最小正周期为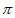 ;②最大值为2;③
;②最大值为2;③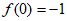 ;④
;④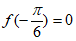 。
。
(Ⅰ)给出函数f(x)的解析式,并说明理由;
(Ⅱ)求函数f(x)的单调递增区间。
18. (本小题满分14分)
随着科技的进步,视频会议系统的前景愈加广阔,其中,小型视频会议软件格外受人青睐,根据调查统计,小型视频会议软件下载量前6名的依次为A,B,C,D,E,F。
在实际中,存在很多软件下载后但并未使用的情况,为此,某调查公司对有视频会议需求的人群进行抽样调查,统计得到这6款软件的下载量W(单位:人次)与使用量U(单位:人次),数据用柱状图表示如下:
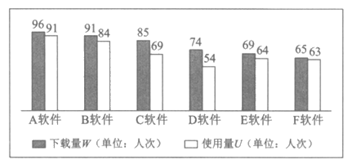
定义软件的使用率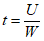 ,当
,当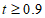 时,称该款软件为”有效下载软件”,调查公司以调查得到的使用率t作为实际中该款软件的使用率。
时,称该款软件为”有效下载软件”,调查公司以调查得到的使用率t作为实际中该款软件的使用率。
(Ⅰ)在这6款软件中任取1款,求该款软件是”有效下载软件”的概率;
(Ⅱ)从这6款软件中随机抽取4款,记其中”有效下载软件”的数量为X,求X的分布列与数学期望;
(Ⅲ)将(Ⅰ)中概率值记为x%,对于市场上所有小型视频会议软件,能否认为这些软件中大约有x%的软件为”有效下载软件”?说明理由。
19. (本小题满分15分)
设函数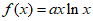 ,其中
,其中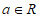 ,曲线
,曲线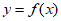 在点
在点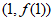 处的切线经过点
处的切线经过点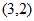 。
。
(Ⅰ)求a的值;
(Ⅱ)求函数f(x)的极值;
(Ⅲ)证明: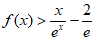 。
。
20. (本小题满分14分)
已知椭圆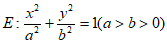 经过点
经过点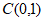 ,离心率为
,离心率为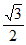 ,O为坐标原点。
,O为坐标原点。
(Ⅰ)求椭圆E的方程;
(Ⅱ)设A,B分别为椭圆E的左、右顶点,D为椭圆E上一点(不在坐标轴上),直线CD交x轴于点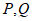 为直线AD上一点,且
为直线AD上一点,且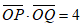 ,求证:
,求证: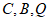 三点共线。
三点共线。
21. (本小题满分14分)
如图,表1是一个由40×20个非负实数组成的40行20列的数表,其中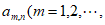
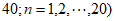 表示位于第m行第n列的数。将表1中每一列的数都按从大到小的次序从上到下重新排列(不改变该数所在的列的位置),得到表2(即
表示位于第m行第n列的数。将表1中每一列的数都按从大到小的次序从上到下重新排列(不改变该数所在的列的位置),得到表2(即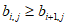 ,其中
,其中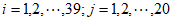 )。
)。
表1 表2
|
| … |
|
|
| … |
| |
|
| … |
|
|
| … |
| |
… | … | … | … | … | … | … | … | |
|
| … |
|
|
| … |
|
(Ⅰ)判断是否存在表1,使得表2中的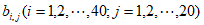 等于
等于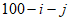 ?等于
?等于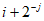 呢?(结论不需要证明)
呢?(结论不需要证明)
(Ⅱ)如果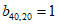 ,且对于任意的
,且对于任意的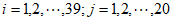 ,都有
,都有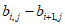 ≥1成立,对于任意的
≥1成立,对于任意的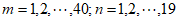 ,都有
,都有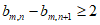 成立,证明:
成立,证明: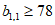 ;
;
(Ⅲ)若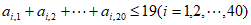 ,求最小的正整数k,使得任给
,求最小的正整数k,使得任给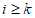 ,都有
,都有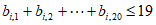 成立。
成立。
【试题答案】
一、选择题:本大题共10小题,每小题4分,共40分。
1. D 2. A 3. D 4. C 5. B
6. B 7. C 8. B 9. C 10. B
二、填空题:本大题共5题,每小题5分,共25分。
11. 30 12. 9,5 13.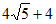
14. 答案不唯一,如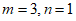 15. ①②
15. ①②
注:第12题第一问3分,第二问2分;第15题全部选对得5分,不选或有错选得0分,其他得3分。
三、解答题:本大题共6小题,共85分,其他正确解答过程,请参照评分标准给分。
16. (本小题满分14分)
解:(Ⅰ)如图,连接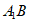 ,设
,设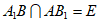 ,并连接DE。
,并连接DE。
由三棱柱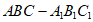 ,得
,得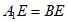 。 2分
。 2分
又因为D是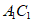 的中点,
的中点,
所以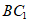 ∥
∥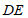 。 4分
。 4分
又因为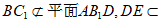 平面
平面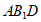 ,
,
所以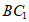 ∥平面
∥平面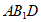 . 6分
. 6分
(Ⅱ)因为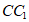 ⊥底面
⊥底面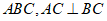 ,
,
所以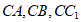 两两垂直,故分别以
两两垂直,故分别以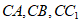 为x轴,y轴,z轴,如图建立空间直角坐标系, 7分
为x轴,y轴,z轴,如图建立空间直角坐标系, 7分
则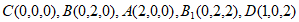 ,
,
所以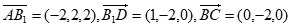 , 8分
, 8分
设平面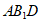 的法向量
的法向量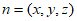 ,
,
由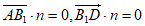 ,得
,得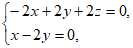
令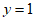 ,得
,得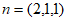 。 11分
。 11分
设直线BC与平面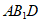 所成的角为
所成的角为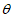 ,
,
则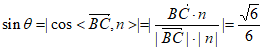 ,
,
所以直线BC与平面AB1D所成角的正弦值为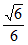 。 14分
。 14分
17. (本小题满分14分)
解:(Ⅰ)若函数f(x)满足条件③,
则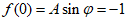 ,
,
这与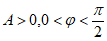 矛盾,故
矛盾,故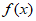 不能满足条件③,
不能满足条件③,
所以函数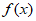 只能满足条件①,②,④。 2分
只能满足条件①,②,④。 2分
由条件①,得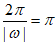 ,
,
又因为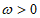 ,所以
,所以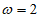 。 4分
。 4分
由条件②,得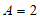 。 5分
。 5分
由条件④,得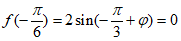 ,
,
又因为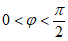 ,所以
,所以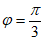 ,
,
所以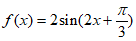 。 8分
。 8分
(Ⅱ)由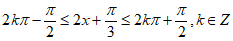 , 10分
, 10分
得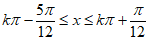 , 12分
, 12分
所以函数f(x)的单调递增区间为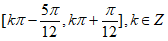 。 14分
。 14分
(注:单调区间写成开区间亦可。)
18. (本小题满分14分)
解:(Ⅰ)根据数据,可得软件A,B,C,D,E,F的使用率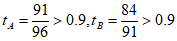 ,
,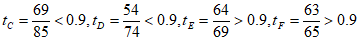 ,
,
所以软件A,B,E,F为”有效下载软件”。 2分
记事件M为”在6款软件中任取1款,该款软件是有效下载软件”, 3分
则事件M的概率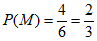 。 4分
。 4分
(Ⅱ)随机变量X的可能取值为2,3,4。 5分
则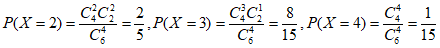 。 8分
。 8分
所以随机变量X的分布列为:
X | 2 | 3 | 4 |
P |
|
|
|
9分
所以随机变量X的数学期望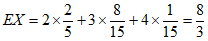 。 10分
。 10分
(Ⅲ)不能认为大约有x%的软件为”有效下载软件”。 12分
理由如下:
若根据这6款软件中”有效下载软件”的概率来估计所有软件中”有效下载软件”的频率,即是用样本估计总体。
用样本估计总体应保证总体中的每个个体被等可能抽取。
但此次调查是”从有视频会议需求的人群”中做调查,且有针对性只选取”下载量排名前6名”的软件,不是从所有软件中随机抽取6款作为样本。
故不能认为大约有x%的软件为”有效下载软件”。 14分
19. (本小题满分15分)
解:(Ⅰ)由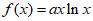 ,得
,得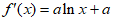 , 2分
, 2分
则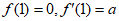 ,
,
所以曲线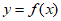 在点
在点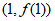 处的切线为
处的切线为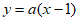 , 4分
, 4分
将点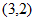 代入切线方程,得
代入切线方程,得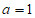 。 5分
。 5分
(Ⅱ)由题意,得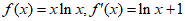 ,
,
令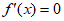 ,得
,得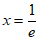 , 7分
, 7分
随着x变化,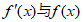 的变化情况如下表所示:
的变化情况如下表所示:
|
|
|
|
| - | 0 | + |
| ↘ | 极小值 | ↗ |
所以函数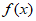 在
在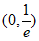 上单调递减,在
上单调递减,在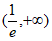 上单调递增, 9分
上单调递增, 9分
所以函数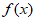 存在极小值,且极小值为
存在极小值,且极小值为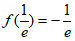 ;函数
;函数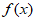 不存在极大值。10分
不存在极大值。10分
(Ⅲ)”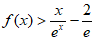 “等价于”
“等价于”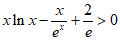 “, 11分
“, 11分
由(Ⅱ),得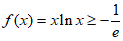 (当且仅当
(当且仅当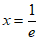 时等号成立), ①
时等号成立), ①
所以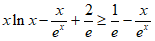 ,
,
故只要证明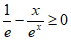 即可(需验证等号不同时成立)。 12分
即可(需验证等号不同时成立)。 12分
设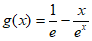 ,
,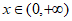 ,则
,则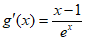 。 13分
。 13分
因为当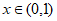 时,
时,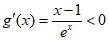 ;当
;当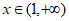 时,
时,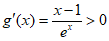 ,
,
所以函数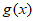 在
在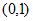 上单调递减,在
上单调递减,在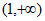 上单调递增,
上单调递增,
所以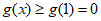 (当且仅当
(当且仅当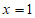 时等号成立)。 ②
时等号成立)。 ②
因为①②两个不等式中的等号不同时成立,
所以当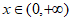 时,
时,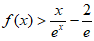 。 15分
。 15分
20. (本小题满分14分)
解:(Ⅰ)由题意,得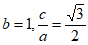 , 2分
, 2分
又因为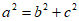 , 3分
, 3分
所以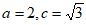 ,
,
故椭圆E的方程为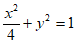 。 5分
。 5分
(Ⅱ)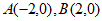 ,
,
设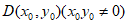 ,则
,则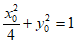 , 6分
, 6分
所以直线CD的方程为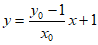 , 7分
, 7分
令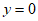 ,得点P的坐标为
,得点P的坐标为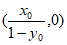 , 8分
, 8分
设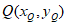 ,由
,由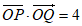 ,得
,得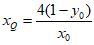 (显然
(显然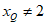 )。 9分
)。 9分
直线AD的方程为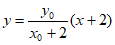 , 10分
, 10分
将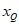 代入,得
代入,得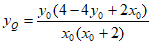 ,即
,即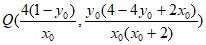 ,11分
,11分
故直线BQ的斜率存在,且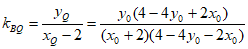 12分
12分
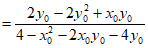
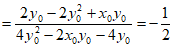 。 13分
。 13分
又因为直线BC的斜率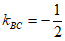 ,
,
所以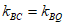 ,即
,即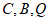 三点共线。 14分
三点共线。 14分
21. (本小题满分14分)
解:(Ⅰ)存在表1,使得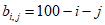 ;不存在表1,使得
;不存在表1,使得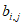 等于
等于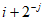 。3分
。3分
(Ⅱ)因为对于任意的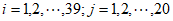 ,都有
,都有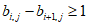 ,
,
所以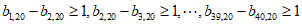 ,
,
所以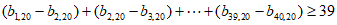 ,
,
即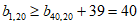 。 6分
。 6分
又因为对于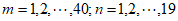 ,都有
,都有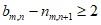 ,
,
所以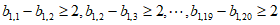 ,
,
所以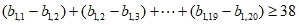 ,
,
所以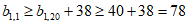 ,
,
即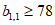 。 8分
。 8分
(Ⅲ)当表l如下图时:
0 | 1 | 1 | … | 1 | 1 |
0 | 1 | 1 | … | 1 | 1 |
1 | 0 | 1 | … | 1 | 1 |
1 | 0 | 1 | … | 1 | 1 |
1 | 1 | 0 | … | 1 | 1 |
1 | 1 | 0 | … | 1 | 1 |
… | … | … | … | … | … |
1 | 1 | 1 | … | 0 | 1 |
1 | 1 | 1 | … | 0 | 1 |
1 | 1 | 1 | … | 1 | 0 |
1 | 1 | 1 | … | 1 | 0 |
其中,每行恰好有1个0和19个1;每列恰好有2个0和38个1;因此每行的和均为19,符合题意。
重新排序后,对应表2中,前38行中每行各数均为1,每行的和均为20;后2行各数均为0,因此k≥39。 10分
以下先证:对于任意满足条件的表1,在表2的前39行中,至少包含原表1中某一行(设为第r行)的全部实数(即包含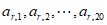 。)
。)
假设表2的前39行中,不能包含原表1中任一行的全部实数。
则表2的前39行中至多含有表1中的40×19=760个数。
这与表2中前39行中共有39×20=780个数矛盾。
所以表2的前39行中,至少包含原表1中某一行(设为第r行)的全部实数。12分
其次,在表2中,根据重排规则得:当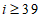 时,
时,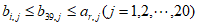 ,
,
所以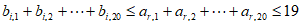 ,
,
所以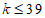 ,
,
综上,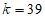 。 14分
。 14分