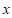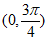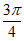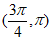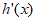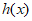本试卷共150分。考试时长120分钟。
第I卷 (选择题 共40分)
一、选择题:本大题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 设集合A={x| |x|<3},B={x| x=2k,k∈Z},则A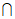 B=
B=
A. {0,2} B. {-2,2} C. {-2,0,2} D. {-2,-l,0,1,2}
2. 若复数z满足z·i=-1+i,则在复平面内z对应的点位于
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3. 下列函数中,值域为R且在区间(0,+∞)上单调递增的是
A. 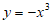 B.
B. 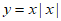 C.
C. 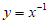 D.
D.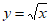
4. 抛物线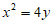 的准线方程为
的准线方程为
A. 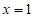 B.
B. 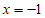 C.
C. 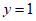 D.
D.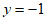
5. 在△ABC中,若a:b:c=4:5:6,则其最大内角的余弦值为
A. 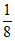 B.
B. 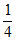 C.
C. 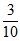 D.
D.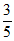
6. 设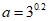 ,
,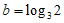 ,
,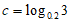 ,则
,则
A. a>c>b B. a>b>c C. b>c>a D. b>a>c
7. 某四棱锥的三视图如图所示,则该四棱锥的体积是
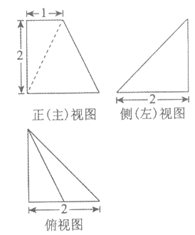
A. 6 B. 4 C. 3 D. 2
8. 若圆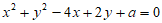 与x轴,y轴均有公共点,则实数a的取值范围是
与x轴,y轴均有公共点,则实数a的取值范围是
A. (-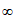 ,1] B. (-
,1] B. (-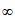 ,0]
,0]
C. [0,+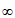 ) D. [5,+∞)
) D. [5,+∞)
9. 若向量a与b不共线,则”a·b<0″是”2| a–b |>|a|+|b|”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D. 既不充分也不必要条件
10. 设函数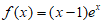 。若关于x的不等式
。若关于x的不等式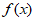 <
<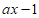 有且仅有一个整数解,则正数a的取值范围是
有且仅有一个整数解,则正数a的取值范围是
A. (0,e] B. (0,e2]
C. (1,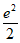 ] D. (1,
] D. (1,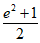 ]
]
第Ⅱ卷 (非选择题 共110分)
二、填空题:本大题共5小题,每小题5分,共25分。
11. 设平面向量a=(1,-2),b=(k,2)满足a⊥b,则|b|=_________。
12. 若双曲线 (a>0)经过点(2,0),则该双曲线渐近线的方程为_________。
(a>0)经过点(2,0),则该双曲线渐近线的方程为_________。
13. 设函数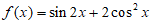 。则函数
。则函数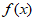 的最小正周期为________;若对于任意x∈R,都有
的最小正周期为________;若对于任意x∈R,都有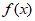 ≤m成立,则实数m的最小值为_________。
≤m成立,则实数m的最小值为_________。
14. 甲、乙、丙、丁四人参加冬季滑雪比赛,其中有两人最终获奖。在比赛结果揭晓之前,四人的猜测如下表,其中”√”表示猜测某人获奖,”×”表示猜测某人未获奖,而”○”则表示对某人是否获奖未发表意见。已知四个人中有且只有两个人的猜测是完全正确的,那么两名获奖者是________,________。
甲获奖 | 乙获奖 | 丙获奖 | 丁获奖 | |
甲的猜测 | √ | × | × | √ |
乙的猜测 | × | ○ | ○ | √ |
丙的猜测 | × | √ | × | √ |
丁的猜测 | ○ | ○ | √ | × |
15. 在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,PA=AB=4,E,F,H分别是棱PB,BC,PD的中点,对于平面EFH截四棱锥P-ABCD所得的截面多边形,有以下三个结论:
①截面的面积等于4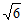 ;
;
②截面是一个五边形;
③直线PC与截面所在的平面EFH无公共点。
其中,所有正确结论的序号是________。
三、解答题:本大题共6小题,共85分。解答应写出必要的文字说明、证明过程或演算步骤。
16. (本小题满分14分)
如图,在几何体ABCDEF中,底面ABCD是边长为2的正方形,DE⊥平面ABCD,DE∥BF,且DE=2BF=2。
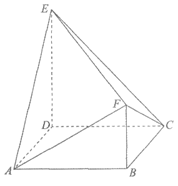
(I)求证:平面BCF∥平面ADE;
(Ⅱ)求钝二面角D-AE-F的余弦值。
17. (本小题满分14分)
从①前n项和Sn=n2+p(p∈R),②an=an+1-3,③a6=11且2 an+1= an + an+2这三个条件中任选一个,补充到下面的问题中,并完成解答。
在数列{an}中,a1=1,_______,其中n∈N*。
(I)求{ an }的通项公式;
(Ⅱ)若a1,an,am成等比数列,其中m,n∈N*,且m>n>1,求m的最小值。
注:如果选择多个条件分别解答,按第一个解答计分。
18. (本小题满分14分)
某花卉企业引进了数百种不同品种的康乃馨,通过试验田培育,得到了这些康乃馨种子在当地环境下的发芽率,并按发芽率分为8组:[0.486,0.536),[0.536,0.586),…,[0.836,0.886)加以统计,得到如图所示的频率分布直方图。
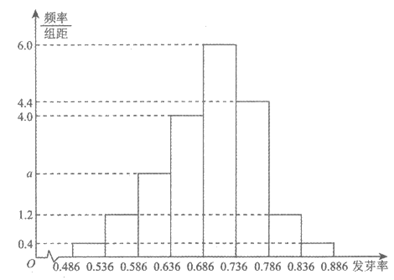
企业对康乃馨的种子进行分级,将发芽率不低于0.736的种子定为”A级”,发芽率低于0.736但不低于0.636的种子定为”B级”,发芽率低于0.636的种子定为”C级”。
(I)现从这些康乃馨种子中随机抽取一种,估计该种子不是”C级”种子的概率;
(Ⅱ)该花卉企业销售花种,且每份”A级”、”B级”、”C级”康乃馨种子的售价分别为20元、15元、10元。某人在市场上随机购买了该企业销售的康乃馨种子两份,共花费X元,以频率为概率,求X的分布列和数学期望;
(Ⅲ)企业改进了花卉培育技术,使得每种康乃馨种子的发芽率提高到原来的1.1倍,那么对于这些康乃馨的种子,与旧的发芽率数据的方差相比,技术改进后发芽率数据的方差是否发生变化?若发生变化,是变大了还是变小了?(结论不需要证明)。
19. (本小题满分14分)
已知椭圆C: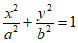 (a>b>0)的离心率为
(a>b>0)的离心率为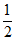 ,右焦点为F,点A(a,0),且|AF|=1。
,右焦点为F,点A(a,0),且|AF|=1。
(I)求椭圆C的方程;
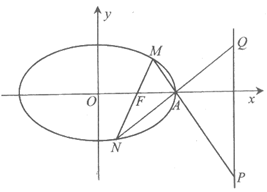
(Ⅱ)过点F的直线l(不与x轴重合)交椭圆C于点M,N,直线MA,NA分别与直线x=4相交于点P,Q。求∠PFQ的大小。
20. (本小题满分15分)
设函数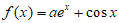 ,其中a∈R。
,其中a∈R。
(I)已知函数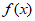 为偶函数,求a的值;
为偶函数,求a的值;
(II)若a=1,证明:当x>0时,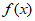 >2;
>2;
(III)若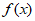 在区间[0,
在区间[0,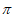 ]内有两个不同的零点,求a的取值范围。
]内有两个不同的零点,求a的取值范围。
21. (本小题满分14分)
设N为正整数,区间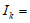 [
[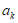 ,
,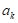 +1](其中
+1](其中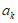 ∈R,k=1,2,…,N)同时满足下列两个条件:
∈R,k=1,2,…,N)同时满足下列两个条件:
①对任意x∈[0,100],存在k使得x∈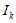 ;
;
②对任意k∈{1,2,…,N},存在x∈[0,100],使得x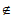 Ii(其中i=1,2,…,k-1,k+1,…,N)。
Ii(其中i=1,2,…,k-1,k+1,…,N)。
(I)判断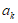 (k=1,2,…,N)能否等于k-1或
(k=1,2,…,N)能否等于k-1或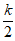 -1;(结论不需要证明)
-1;(结论不需要证明)
(Ⅱ)求N的最小值;
(Ⅲ)研究N是否存在最大值,若存在,求出N的最大值;若不存在,说明理由。
参考答案
一、选择题:本大题共10小题,每小题4分,共40分。
1. C 2. A 3. B 4. D 5. A
6. B 7. D 8. A 9. A 10. D
二、填空题:本大题共5小题,每小题5分,共25分。
11. 2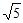 12.
12. 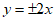 13.
13. 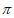 ,
,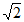 +1
+1
14. 乙,丁 15. ②③
注:第14题全部选对得5分,其他得0分;第15题全部选对得5分,不选或有错选得0分,其他得3分。
三、解答题:本大题共6小题,共85分。其他正确解答过程,请参照评分标准给分。
16. (本小题满分14分)
解:(I)因为DE∥BF,DE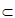 平面ADE,BF
平面ADE,BF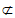 平面ADE,
平面ADE,
所以BF∥平面ADE。 ………………3分
同理,得BC∥平面ADE。
又因为BC BF=B,BC
BF=B,BC 平面BCF,BF
平面BCF,BF 平面BCF,
平面BCF,
所以平面BCF∥平面ADE。 ………………6分
(II)由DE⊥平面ABCD,底面ABCD为正方形,
得DA,DC,DE两两垂直,故分别以DA,DC,DE为x轴,y轴,z轴,如图建立空间直角坐标系, ………………7分
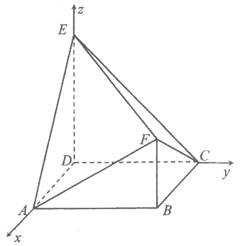
则D(0,0,0),E(0,0,2),F(2,2,1),A(2,0,0),
所以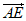 =(-2,0,2),
=(-2,0,2),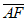 =(0,2,1)。……·8分
=(0,2,1)。……·8分
设平面AEF的法向量n=(x,y,z),
由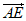 ·n=0,
·n=0,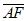 ·n=0,得
·n=0,得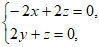
令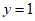 ,得n=(-2,1,-2)。 ………………11分
,得n=(-2,1,-2)。 ………………11分
平面DAE的法向量m=(0,1,0)。
设钝二面角D-AE-F的平面角为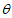 ,
,
则| cos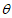 |=|cos<m,n>|=|
|=|cos<m,n>|=|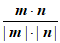 |=
|=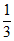 ,
,
所以cos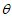 =-
=-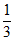 ,即钝二面角D-AE-F的余弦值为-
,即钝二面角D-AE-F的余弦值为-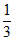 。 ………………14分
。 ………………14分
17. (本小题满分14分)
解:选择①:
(I)当n=l时,由S1=a1=1,得p=0。 ………………2分
当n≥2时,由题意,得Sn-1=(n-1)2, ………………3分
所以an=Sn-Sn-1=2n-1(n≥2)。 ………………5分
经检验,a1=1符合上式,
所以an=2n-1(n∈N*)。 ………………6分
(II)由a1, an,am成等比数列,得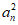 = a1 am, ………………8分
= a1 am, ………………8分
即(2n-1)2=1×(2m-1)。 ………………9分
化简,得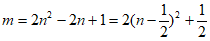 , ………………11分
, ………………11分
因为m,n是大于1的正整数,且m>n,
所以当n=2时,m有最小值5。 ………………14分
选择②:
(I)因为an= an+1-3,所以an+1– an=3。 ………………2分
所以数列{ an}是公差d=3的等差数列。 ………………4分
所以an= a1+(n-1)d=3n-2(n∈N*)。 ………………6分
(II)由a1,an,am成等比数列,得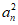 = a1am, ………………8分
= a1am, ………………8分
即(3n-2)2=1×(3m-2)。 ………………9分
化简,得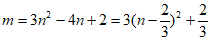 , ………………11分
, ………………11分
因为m,n是大于1的正整数,且m>n,
所以当n=2时,m取到最小值6。 ………………14分
选择③:
(I)由2an+1= an + an+2,得an
+1– an = an+2– an
+1。
所以数列{ an}是等差数列。 ………………2分
又因为a1=1,a6= a1+5d=11,
所以d=2。 ………………4分
所以an= a1+(n-1)d=2n-1(n∈N*)。 ………………6分
(II)因为a1,an,am成等比数列,所以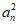 = a1am, ………………8分
= a1am, ………………8分
即(2n-1)2=1×(2m-1)。 ………………9分
化简,得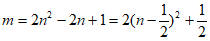 , …………11分
, …………11分
因为m,n是大于1的正整数,且m>n,
所以当n=2时,m有最小值5。 ………………14分
18. (本小题满分14分)
解:(I)设事件M为:”从这些康乃馨种子中随机抽取一种,且该种子不是”C级”种子”,
………………1分
由图表,得(0.4+1.2+a+4.0+6.0+4.4+1.2+0.4)×0.05=1,
解得a=2.4。 ………………2分
由图表,知”C级”种子的频率为(0.4+1.2+2.4)×0.05=0.2, …………3分
故可估计从这些康乃馨种子中随机抽取一种,该种子是”C级”的概率为0.2。
因为事件M与事件”从这些康乃馨种子中随机抽取一种,且该种子是”C级”种子”为对立事件,
所以事件M的概率P(M)=l-0.2=0.8。 ………………5分
(II)由题意,任取一种种子,恰好是”A级”康乃馨的概率为(4.4+1.2+0.4)×0.05=0.3,
恰好是”B级”康乃馨的概率为(4.0+6.0)×0.05=0.5,
恰好是”C级”的概率为(0.4+1.2+2.4)×0.05=0.2。 ………………7分
随机变量X的可能取值有20,25,30,35,40,
且P(X=20)=0.2×0.2=0.04,
P(X=25)=0.2×0.5+0.5×0.2=0.2,
P(X=30)=0.5×0.5+0.3×0.2+0.2×0.3=0.37,
P(X=35)=0.3×0.5+0.5×0.3=0.3,
P(X=40)=0.3×0.3=0.09。 ………………9分
所以X的分布列为:
X | 20 | 25 | 30 | 35 | 40 |
P | 0.04 | 0.2 | 0.37 | 0.3 | 0.09 |
………………10分
故X的数学期望E(X)=20×0.04+25×0.2+30×0.37+35×0.3+40×0.09=31。
………………11分
(III)与旧的发芽率数据的方差相比,技术改进后发芽率数据的方差变大了。……14分
19. (本小题满分14分)
解:(I)由题意得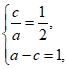
解得a=2,c=1, ……………3分
从而b=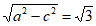 ,
,
所以椭圆C的方程为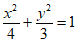 。 …5分
。 …5分
(II)当直线l的斜率不存在时,有M(1,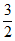 ),N(1,-
),N(1,-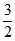 ),P(4,-3),Q(4,3),F(1,0),
),P(4,-3),Q(4,3),F(1,0),
则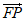 =(3,-3),
=(3,-3), =(3,3),故
=(3,3),故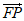 ·
· =0,即∠PFQ=90°。………6分
=0,即∠PFQ=90°。………6分
当直线l的斜率存在时,设l:y=k(x-1),其中k≠0。 ………………7分
联立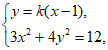 得
得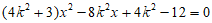 ………………8分
………………8分
由题意,知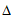 >0恒成立,
>0恒成立,
设M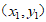 ,
,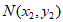 ,则
,则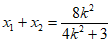 ,
, 。……9分
。……9分
直线MA的方程为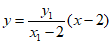 。 ………………10分
。 ………………10分
令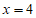 ,得
,得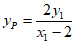 ,即
,即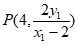 。 ………………11分
。 ………………11分
同理可得Q(4,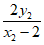 )。 ………………12分
)。 ………………12分
所以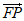 =(3,
=(3,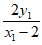 ),
), =(3,
=(3,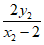 )。
)。
因为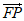 ·
· =
=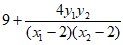 =
=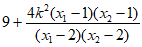
=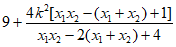
=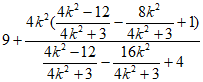 =
=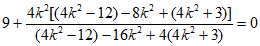 ,
,
所以∠PFQ=90°。
综上,∠PFQ=90°。 ………………14分
20. (本小题满分15分)
解:(I)函数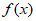 为偶函数,
为偶函数,
所以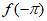 =
=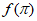 ,即
,即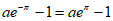 ………………2分
………………2分
解得a=0。
验证知a=0符合题意。 ………………4分
(II)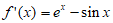 。 ………………6分
。 ………………6分
由x>0,得ex>1,sinx∈[-1,1], ………………7分
则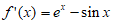 >0,即
>0,即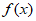 在(0,+
在(0,+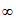 )上为增函数。
)上为增函数。
故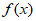 >
>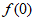 =2,即
=2,即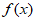 >2。 ………………9分
>2。 ………………9分
(III)由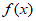 =
=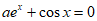 ,得
,得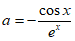 。
。
设函数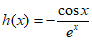 ,x∈[0,
,x∈[0,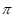 ],………………10分
],………………10分
则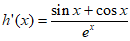 。 ………………11分
。 ………………11分
令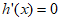 ,得
,得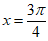 。
。
随着x变化,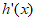 与
与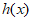 的变化情况如下表所示:
的变化情况如下表所示:
|
|
|
|
| + | 0 | – |
| ↗ | 极大值 | ↘ |
所以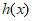 在
在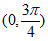 上单调递增,在
上单调递增,在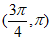 上单调递减。 ………………13分
上单调递减。 ………………13分
又因为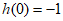 ,
,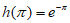 ,
,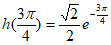 ,
,
所以当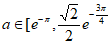 ),方程
),方程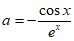 在区间[0,
在区间[0,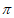 ]内有两个不同解,且在区间
]内有两个不同解,且在区间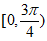 与(
与(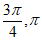 ]上各有一个解。
]上各有一个解。
即所求实数a的取值范围为[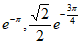 )。 ………………15分
)。 ………………15分
21. (本小题满分14分)
解:(I)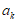 可以等于k-1,但
可以等于k-1,但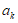 不能等于
不能等于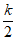 -1。 ………………3分
-1。 ………………3分
(II)记b–a为区间[a,b]的长度,
则区间[0,100]的长度为100,Ik的长度为1。
由①,得N≥100。 ……………6分
又因为I1=[0,1],I2=[1,2],…,I100=[99,100]显然满足条件①,②。
所以N的最小值为100。 ………………8分
(III)N的最大值存在,且为200。 ………………9分
解答如下:
(1)首先,证明N≤200。
由②,得I1,I2,…,IN互不相同,且对于任意k,Ik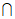 [0,100]≠Ø。
[0,100]≠Ø。
不妨设a1< a2<…< an<…。
如果a2≤0,那么对于条件②,当k=1时,不存在x∈[0,100],使得x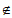 Ii(i=2,3,…,N)。
Ii(i=2,3,…,N)。
这与题意不符,故a2>0。 ………………10分
如果ak+1≤ak-1+1,那么Ik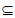 Ik-1
Ik-1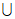 Ik+1,
Ik+1,
这与条件②中”存在x∈[0,100],使得x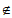 Ii(i=l,2,…,k-l,k+1,…N)”矛盾,
Ii(i=l,2,…,k-l,k+1,…N)”矛盾,
故ak+1>ak-1+1。
所以a4> a2+1>l,a6> a4+1>2,…,a200> a198+1>99,
则a200+1>100。
故I1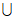 I2
I2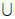 …
…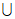 I200
I200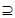 [0,100]。
[0,100]。
若存在I201,这与条件②中”存在x∈[0,100],使得x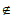 Ii(i=1,2,…,200)”矛盾,
Ii(i=1,2,…,200)”矛盾,
所以N≤200。 ………………12分
(2)给出N=200存在的例子。
令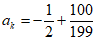 (k-1),其中k=1,2,…,200,即a1,a2,…,a200为等差数列,公差
(k-1),其中k=1,2,…,200,即a1,a2,…,a200为等差数列,公差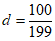 。
。
由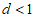 ,知
,知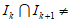 Ø,则易得I1
Ø,则易得I1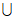 I2
I2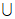 …
…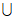 I200=[-
I200=[-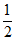 ,
,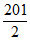 ],
],
所以I1,I2,…,I200满足条件①。
又公差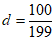 >
>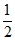 ,
,
所以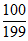 (k-1)∈Ik,
(k-1)∈Ik,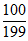 (k-1)
(k-1)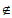 Ii(i=1,2,…,k-1,k+l,…N)。(注:
Ii(i=1,2,…,k-1,k+l,…N)。(注: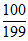 (k-1)为区间Ik的中点对应的数)
(k-1)为区间Ik的中点对应的数)
所以I1,I2,…,I200满足条件②。
综合(1)(2)可知N的最大值存在,且为200。 ………………14分