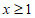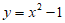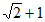本试卷共三道大题,28道小题。满分100分。考试时间120分钟。
一、选择题(本题共16分,每小题2分)
第1-8题均有四个选项,符合题意的选项只有一个。
1. 北京大兴国际机场目前是全球建设规模最大的机场,2019年9月25日正式通航,预计到2022年机场旅客吞吐量将达到45 000 000人次,将45 000 000用科学记数法表示为
A. 45×106 B. 4.5×107 C. 4.5×108 D. 0.45×108
2. 下图是某个几何体的三视图,该几何体是
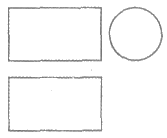
A. 圆锥 B. 圆柱
C. 长方体 D. 正三棱柱
3. 下面的图形中,既是轴对称图形又是中心对称图形的是
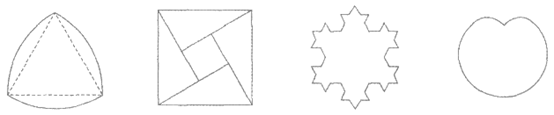
A B C D
4. 在数轴上,点A,B表示的数互为相反数,若点A在点B的左侧,且AB=2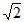 ,则点A,点B表示的数分别是
,则点A,点B表示的数分别是
A. –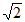 ,
,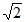 B.
B. 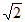 ,-
,-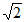
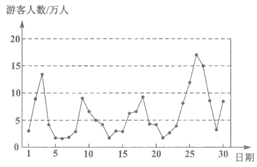
C. 0,2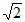 D. -2
D. -2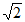 ,2
,2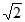
5. 如图,AB是⊙O的直径,C,D是⊙O上的两点。若∠CAB=65°,则∠ADC的度数为
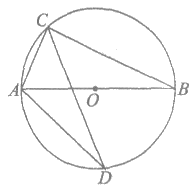
A. 65° B. 35° C. 32.5° D. 25°
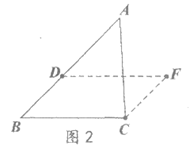
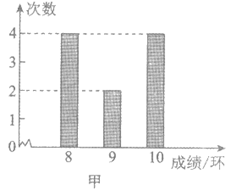
6. 甲、乙两名运动员的10次射击成绩(单位:环)如图所示,甲、乙两名运动员射击成绩的平均数依次记为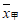 ,
,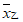 ,射击成绩的方差依次记为
,射击成绩的方差依次记为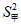 ,
,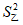 ,则下列关系中完全正确的是
,则下列关系中完全正确的是
A. 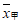 =
=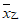 ,
,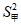 >
>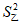 B.
B. 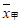 =
=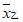 ,
,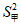 <
<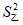
C. 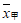 >
>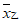 ,
,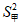 >
>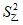 D.
D. 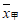 <
<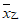 ,
,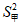 <
<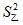
7. 如图,在数学实践活动课上,小明同学打算通过测量树的影长计算树的高度。阳光下他测得长1.0 m的竹竿落在地面上的影长为0.9 m。在同一时刻测量树的影长时,他发现树的影子有一部分落在地面上,还有一部分落在墙面上。他测得这棵树落在地面上的影长BD为2.7 m,落在墙面上的影长CD为1.0 m,则这棵树的高度是
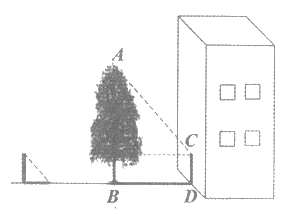
A. 6.0m B. 5.0m
C. 4.0 m D. 3.0 m
8. 设m是非零实数,给出下列四个命题:
①若-1<m<0,则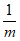 <m<m2; ②若m>1,则
<m<m2; ②若m>1,则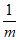 <m2<m;
<m2<m;
③若m<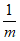 <m2,则m<0; ④m2<m<
<m2,则m<0; ④m2<m<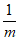 ,则0<m<1。
,则0<m<1。
其中命题成立的序号是
A. ①③ B. ①④ C. ②③ D. ③④
二、填空题 (本题共16分,每小题2分)
9. 若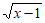 在实数范围内有意义,则实数x的取值范围是________。
在实数范围内有意义,则实数x的取值范围是________。
10. 若多边形的内角和是外角和的2倍,则该多边形是________边形。
11. 已知y是以x为自变量的二次函数,且当x=0时,y的最小值为-1,写出一个满足上述条件的二次函数表达式________.
12. 如果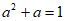 ,那么代数式
,那么代数式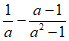 的值是________。
的值是________。
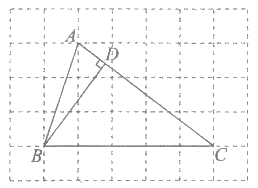
13. 如图,在正方形ABCD中,BE平分∠CBD,EF⊥BD于点F。若DE=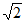 ,则BC的长为________。
,则BC的长为________。
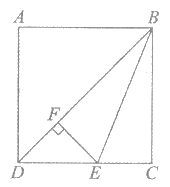
14. 如图,△ABC的顶点A,B,C都在边长为1的正方形网格的格点上,BD⊥AC于点D,则AC的长为_______,BD的长为_________。
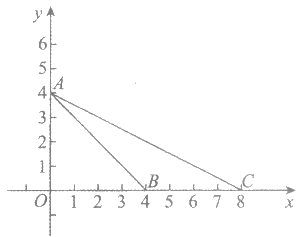
15. 如图,在平面直角坐标系xOy中,点A,B,C的坐标分别是(0,4),(4,0),(8,0),⊙M是△ABC的外接圆,则点M的坐标为________。
16. 某景区为了解游客人数的变化规律,提高旅游服务质量,收集并整理了某月(30天)接待游客人数(单位:万人)的数据,绘制了下面的统计图和统计表。
|
|
根据以上信息,以下四个判断中,正确的是________(填写所有正确结论的序号)。
①该景区这个月游玩环境评价为”拥挤或严重拥挤”的天数仅有4天;
②该景区这个月每日接待游客人数的中位数在5~10万人之间;
③该景区这个月平均每日接待游客人数低于5万人;
④这个月1日至5日的五天中,如果某人曾经随机选择其中的两天到该景区游玩,那么他”这两天游玩环境评价均为好”的可能性为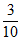 。
。
三、解答题(本题共68分,第17-2l题,每小题5分,第22-24题,每小题6分,第25题5分,第26题6分,第27-28题,每小题7分)
解答应写出文字说明、演算步骤或证明过程。
17. 计算: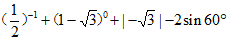 。
。
18. 解不等式组: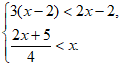
19. 关于x的一元二次方程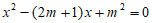 有两个实数根。
有两个实数根。
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根。
20. 如图,在□ABCD中,对角线AC,BD交于点O,OA=OB,过点B作BE⊥AC于点E。
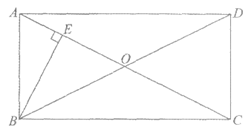
(1)求证:□ABCD是矩形;
(2)若AD=2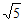 ,cos∠ABE=
,cos∠ABE=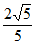 ,求AC的长。
,求AC的长。
21. 先阅读下列材料,再解答问题。
尺规作图
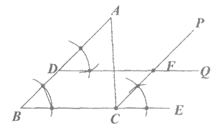
已知:△ABC,D是边AB上一点,如图l,
求作:四边形DBCF,使得四边形DBCF是平行四边形。
小明的做法如下:
(1)设计方案 |
先画一个符合题意的草图,如图2,
再分析实现目标的具体方法, 依据:两组对边分别平行的四边形是平行四边形。 |
(2)设计作图步骤,完成作图 |
作法:如图,
①延长BC至点E; ②分别作∠ECP=∠ABE,∠ADQ=∠ABE; ③DQ与CP交于点F。 ∴四边形DBCF即为所求。 |
(3)推理论证 |
证明:∵∠ECP=∠ABE, ∴CP∥BA。 同理,DQ∥BE。 ∴四边形DBCF是平行四边形。 |
请你参考小明的做法,再设计一种尺规作图的方法(与小明的方法不同),使得画出的四边形DBCF是平行四边形,并证明。
22. 运用语音识别输入软件可以提高文字输入的速度。为了解A,B两种语音识别输入软件的准确性,小秦同学随机选取了20段话,其中每段话都含100个文字(不计标点符号)。在保持相同语速的条件下,他用标准普通话朗读每段话来测试这两种语音识别输入软件的准确性。他的测试和分析过程如下,请补充完整。
(1)收集数据 两种软件每次识别正确的字数记录如下:
A | 98 | 98 | 92 | 92 | 92 | 92 | 92 | 89 | 89 | 85 |
84 | 84 | 83 | 83 | 79 | 79 | 78 | 78 | 69 | 58 | |
B | 99 | 96 | 96 | 96 | 96 | 96 | 96 | 94 | 92 | 89 |
88 | 85 | 80 | 78 | 72 | 72 | 71 | 65 | 58 | 55 |
(2)整理、描述数据 根据上面得到的两组样本数据,绘制了频数分布直方图:
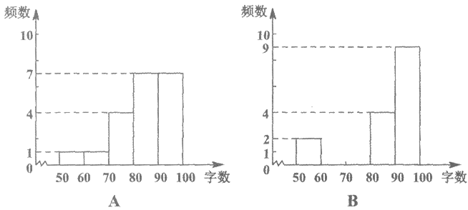
(3)分析数据 两组样本数据的平均数、众数、中位数、方差如下表所示:
平均数 | 众数 | 中位数 | 方差 | |
A | 84.7 | 84.5 | 88.91 | |
B | 83.7 | 96 | 184.01 |
(4)得出结论 根据以上信息,判断_______种语音识别输入软件的准确性较好,理由如下:_____________(至少从两个不同的角度说明判断的合理性)。
23. 如图,四边形OABC中,∠OAB=90°,OA=OC,BA=BC。以O为圆心,以OA为半径作⊙O。
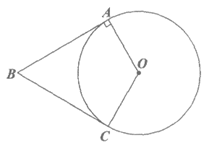
(1)求证:BC是⊙O的切线;
(2)连接BO并延长交⊙O于点D,延长AO交⊙O于点E,与BC的延长线交于点F,若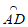 =
=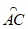 ,
,
①补全图形;
②求证:OF=OB。
24. 如图,在△ABC中,AB=4 cm,BC=5 cm。P是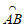 上的动点,设A,P两点间的距离为xcm,B,P两点间的距离为y1 cm,C,P两点间的距离为y2cm。
上的动点,设A,P两点间的距离为xcm,B,P两点间的距离为y1 cm,C,P两点间的距离为y2cm。
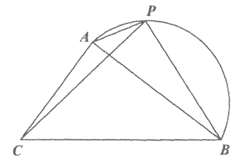
小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究。下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 |
y1/cm | 4.00 | 3.69 | 2.13 | 0 | |
y2/cm | 3.00 | 3.91 | 4.71 | 5.23 | 5 |
(2)在同一平面直角坐标系 中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;
中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;
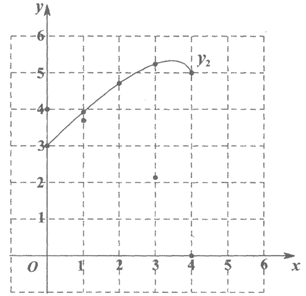
(3)结合函数图象,
①当△PBC为等腰三角形时,AP的长度约为________cm:
②记 所在圆的圆心为点O,当直线PC恰好经过点O时,PC的长度约为________cm。
所在圆的圆心为点O,当直线PC恰好经过点O时,PC的长度约为________cm。
25. 在平面直角坐标系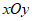 中,直线
中,直线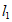 :y=kx+2k(k>0)与x轴交于点A,与y轴交于点B,与函数
:y=kx+2k(k>0)与x轴交于点A,与y轴交于点B,与函数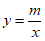 (x>0)的图象的交点P位于第一象限。
(x>0)的图象的交点P位于第一象限。
(1)若点P的坐标为(1,6),
①求m的值及点A的坐标;
②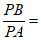 __________;
__________;
(2)直线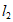 :y=2kx-2与y轴交于点C,与直线
:y=2kx-2与y轴交于点C,与直线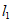 交于点Q,若点P的横坐标为l,
交于点Q,若点P的横坐标为l,
①写出点P的坐标(用含k的式子表示);
②当PQ≤PA时,求m的取值范围。
26. 已知抛物线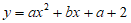 (a≠0)与x轴交于点A(
(a≠0)与x轴交于点A(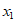 ,0),点B(x2,0)(点A在点B的左侧),抛物线的对称轴为直线x=-1。
,0),点B(x2,0)(点A在点B的左侧),抛物线的对称轴为直线x=-1。
(1)若点A的坐标为(-3,0),求抛物线的表达式及点B的坐标;
(2)C是第三象限的点,且点C的横坐标为-2,若抛物线恰好经过点C,直接写出x2的取值范围;
(3)抛物线的对称轴与x轴交于点D,点P在抛物线上,且∠DOP=45°,若抛物线上满足条件的点P恰有4个,结合图象,求a的取值范围。
27. 如图,在等腰直角△ABC中,∠ACB=90°。点P在线段BC上,延长BC至点Q,使得CQ=CP,连接AP,AQ。过点B作BD⊥AQ于点D,交AP于点E,交AC于点F。K是线段AD上的一个动点(与点A,D不重合),过点K作GN⊥AP于点H,交AB于点G,交AC于点M,交FD的延长线于点N。
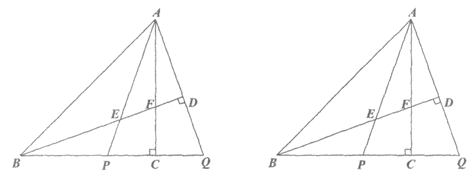
图1 备用图
(1)依题意补全图1;
(2)求证:NM=NF;
(3)若AM=CP,用等式表示线段AE,GN与BN之间的数量关系,并证明。
28. 对于平面直角坐标系 中的图形W1和图形W2,给出如下定义:在图形W1上存在两点A,B(点A与点B可以重合),在图形W2上存在两点M,N(点M与点N可以重合),使得AM=2BN,则称图形W1和图形W2满足限距关系。
中的图形W1和图形W2,给出如下定义:在图形W1上存在两点A,B(点A与点B可以重合),在图形W2上存在两点M,N(点M与点N可以重合),使得AM=2BN,则称图形W1和图形W2满足限距关系。
(1)如图1,点C(1,0),D(-1,0),E(0,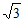 ),点P在线段DE上运动(点P可以与点D,E重合),连接OP,CP。
),点P在线段DE上运动(点P可以与点D,E重合),连接OP,CP。
①线段OP的最小值为_______,最大值为_______;线段CP的取值范围是_______;
②在点O,点C中,点_______与线段DE满足限距关系;
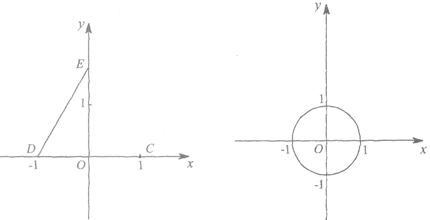
图1 图2
(2)如图2,⊙O的半径为l,直线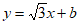 (b>0)与x轴、y轴分别交于点F,G。若线段FG与⊙O满足限距关系,求b的取值范围;
(b>0)与x轴、y轴分别交于点F,G。若线段FG与⊙O满足限距关系,求b的取值范围;
(3)⊙O的半径为r(r>0),点H,K是⊙O上的两个点,分别以H,K为圆心,1为半径作圆得到⊙H和⊙K,若对于任意点H,K,⊙H和⊙K都满足限距关系,直接写出r的取值范围。
参考答案
一、选择题(本题共16分,每小题2分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | B | B | C | A | D | A | C | B |
二、填空题(本题共16分,每小题2分)
9 | 10 | 11 | 12 |
| 六 | 答案不唯一,如: | 1 |
13 | 14 | 15 | 16 |
| 5,3 | (6,6) |
|
三、解答题(本题共68分,第17-21题,每小题5分,第22-24题,每小题6分,第25题5分,第26题6分,第27-28题,每小题7分)
17. 解: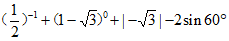
=2+l+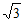 -2×
-2×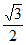
=3。 ……..5分
18. 解:原不等式组为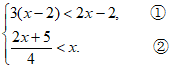
解不等式①,得x<4。
解不等式②,得x>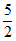 。
。
∴原不等式组的解集为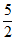 <x<4。 ……..5分
<x<4。 ……..5分
19. 解:(1)依题意,得△=[-(2m+1)]2-4×1×m2。
=4m+1≥0。
解得m≥-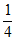 。
。
(2)答案不唯一,如:m=0,
此时方程为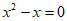 。
。
解得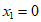 ,
,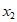 =1。………………………………………5分
=1。………………………………………5分
20. (1)证明:∵四边形ABCD是平行四边形,
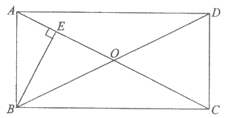
∴OA=OC,OB=OD。
∵OA=OB,
∴OA=OC=OB=OD。
∴AC=BD。
∴□ABCD是矩形。
(2)解:∵四边形ABCD是矩形,
∴∠BAD=∠ADC=90°。
∴∠BAC+∠CAD=90°。
∵BE⊥AC,
∴∠BAC+∠ABE=90°。
∴∠CAD=∠ABE。
在Rt△ACD中,AD=2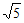 ,cos∠CAD=cos∠ABE=
,cos∠CAD=cos∠ABE=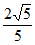 ,
,
∴AC=5。 ………………………………………5分
21. 答案不唯一,如:
(1)两组对边分别相等的四边形是平行四边形。
(2)如图。
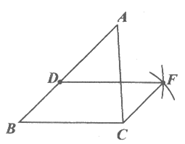
(3)证明:∵CF=BD,DF=BC,
∴四边形DBCF是平行四边形。……………………………………5分
22. 解:(2)
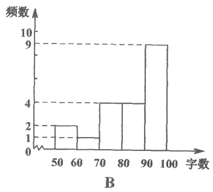
(3)
平均数 | 众数 | 中位数 | 方差 | |
A | 92 | |||
B | 88.5 |
(4)答案不唯一,理由须支撑推断的结论。
………………………………………………………………6分
23. (1)证明:连接AC,
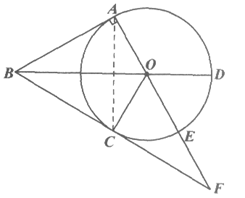
∵OC=OA。
∴点C在⊙O上。
∵OA=OC,BA=BC,
∴∠OAC=∠OCA,∠BAC=∠BCA。
∴∠OCB=∠OAB=90°。
∴OC⊥BC于点C。
∴BC是⊙O切线。
(2)①补全图形。
②证明:∵BA,BC是⊙O的两条切线,切点分别为A,C,
∴BA=BC,∠DBA=∠DBC。
∴BD是AC的垂直平分线。
∵OA=OC,
∴∠AOB=∠COB。
∵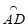 =
=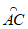 ,AE为⊙O的直径,
,AE为⊙O的直径,
∴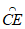 =
=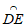 。
。
∴∠COE=∠DOE。
∵∠AOB=∠DOE。
∴∠AOB=∠BOC=∠COE=60°。
∵BC是⊙O的切线,切点为C,
∴∠OCB=∠OCF=90°。
∴∠OBC=∠OFC=30°。
∴OF=OB. ………………………………………………………6分
24. 解:(1)
x/cm | 0 | 1 | 2 | 3 | 4 |
y1/cm | 3.09 | ||||
y2/cm |
(2)画出函数y1的图象;
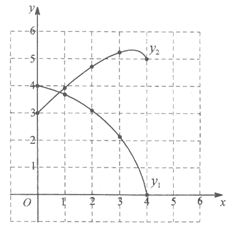
(3)①0.83或2.49。
②5.32。
…………………………………………………6分
25. 解:(1)①令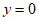 ,则
,则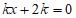 。
。
∵k>0,解得x=-2。
∴点A的坐标为(-2,0)。
∵点P的坐标为(1,6),
∴m=6。
②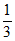 。
。
(2)①P(1,3k)。
②依题意,得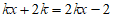 ,
,
解得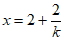 。
。
∴点Q的横坐标为2+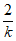 ,
,
∵2+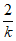 >1(k>0),
>1(k>0),
∴点Q在点P的右侧。
如图,分别过点P,Q作PM⊥x轴于M,QN⊥x轴于N,
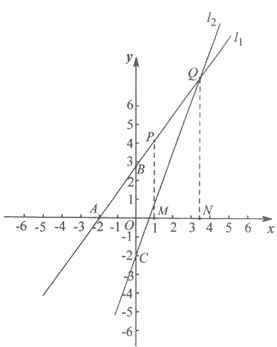
则点M,点N的横坐标分别为1,2+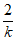 。
。
若PQ=PA,则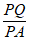 =1。
=1。
∴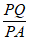 =
=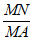 =1
=1
∴MN=MA。
∴2+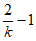 =3,解得k=1。
=3,解得k=1。
∵MA=3,
∴当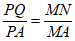 ≤1时,k≥1。
≤1时,k≥1。
∴m=3k≥3。
∴当PQ≤PA时,m≥3。………………………………………5分
26. 解:(1)∵抛物线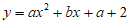 的对称轴为直线x=-1,
的对称轴为直线x=-1,
∴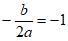 。
。
∴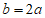 。
。
∴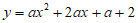 化为y=a(x+1)2+2。
化为y=a(x+1)2+2。
将点A(-3,0)代入y=a(x+1)2+2中,得a=-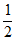 。
。
∴抛物线的表达式为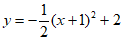 ,此时点B的坐标为(1,0)。
,此时点B的坐标为(1,0)。
(2)-1< <0。
<0。
(3)∵抛物线的顶点为(-1,2),
∴点D的坐标为(-1,0)。
∵∠DOP=45°,且抛物线上满足条件的点P恰有4个,
∴抛物线与x轴的交点都在原点的左侧。
∴满足条件的点P在x轴上方有2个,在x轴下方也有2个。
∴a+2<0。
解得a<-2。
∴a的取值范围是a<-2。………………………………6分
27. (1)补全图形,如图1。
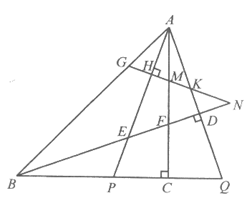
图1
证明:(2)∵CQ=CP,∠ACB=90°,
∴AP=AQ。
∴∠APQ=∠Q。
∵BD⊥AQ,
∴∠QBD+∠Q=∠QBD+∠BFC=90°。
∴∠Q=∠BFC。
∵∠MFN=∠BFC。
∴∠MFN=∠Q。
同理,∠NMF=∠APQ。
∴∠MFN=∠FMN。
∴NM=NF。
(3)连接CE,如图2。
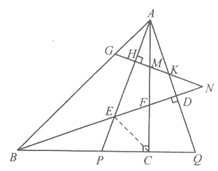
图2
由(1)可得∠PAC=∠FBC,
∵∠ACB=90°,AC=BC,
∴△APC≌△BFC。
∴CP=CF。
∵AM=CP,
∴AM=CF。
∵∠CAB=∠CBA=45°。
∴∠EAB=∠EBA。
∴AE=BE。
又∵AC=BC,
∴CE所在直线是AB的垂直平分线。
∴∠ECB=∠ECA=45°。
∴∠GAM=∠ECF=45°。
由(1)可得∠AMG=∠CFE,
∴△AGM≌△CEF。
∴GM=EF。
∵BN=BE+EF+FN=AE+GM+MN。
∴BN=AE+GN。…………………………………………7分
28. 解:(1)①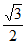 ,
,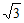 ;
;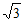 ≤CP≤2;
≤CP≤2;
②O。
(2)直线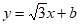 与x轴、y轴分别交于点F,G(0,b),
与x轴、y轴分别交于点F,G(0,b),
当0<b<1时,线段FG在⊙O的内部,与⊙O无公共点,
此时⊙O上的点到线段FG的最小距离为1-b,最大距离为1+b。
∵线段FG与⊙O满足限距关系,
∴1+b≥2(1-b)。
解得b≥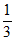 。
。
∴b的取值范围是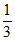 ≤b<1。
≤b<1。
当1≤b≤2时,线段FG与⊙O有公共点,线段FG与⊙O满足限距关系。
当b>2时,线段FG在⊙O的外部,与⊙O无公共点,
此时⊙O上的点到线段FG的最小距离为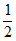 b-1,最大距离为b+1。
b-1,最大距离为b+1。
∵线段FG与⊙O满足限距关系,
∴b+1≥2(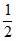 b-1)。
b-1)。
而b+1>2(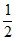 b-1)总成立。
b-1)总成立。
∴当b>2时,线段FG与⊙O满足限距关系。
综上,b的取值范围是b≥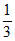 。
。
(3)0<r≤3。……………………………………………7分