本试卷共三道大题,28道小题。满分100分。考试时间120分钟。
一、选择题(本题共16分,每小题2分)
第1-8题均有四个选项,符合题意的选项只有一个.
1.下列各组图形中,能将其中一个图形经过平移变换得到另一个图形的是

2.中国国家航天局2020年4月24日在”中国航天日”之际宣布,将中国行星探测任务命名为”天问”,将中国首次火星探测任务命名为”天问一号”. 火星具有与地球十分相近的环境,与地球最近的时候距离约5 500万千米,将5 500用科学记数法表示为
(A)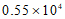 (B)
(B)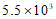 (C)
(C)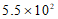 (D)
(D)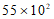
3.图1是某个几何体的平面展开图,该几何体是
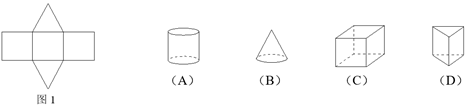
4.下列运算中,正确的是
(A)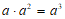 (B)
(B)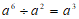 (C)
(C) 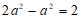 (D)
(D)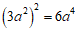
5.如图,实数a,b在数轴上的对应点的位置如图所示,则正确的结论是
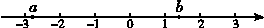
(A)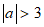 (B)
(B)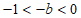 (C)
(C)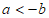 (D)
(D)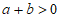
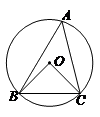
6.如图,△ABC内接于⊙O,若∠A=45°,OC=2,则BC的长为
(A)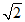 (B)
(B)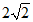
(C)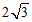 (D)4
(D)4
7.某人开车从家出发去植物园游玩,设汽车行驶的路程为S(千米),所用时间为t(分),S与t之间的函数关系如图所示.若他早上8点从家出发,汽车在途中停车加油一次,则下列描述中,不正确的是
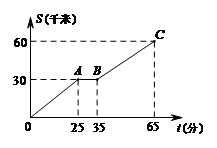
(A)汽车行驶到一半路程时,停车加油用时10分钟
(B)汽车一共行驶了60千米的路程,上午9点5分到达植物园
(C)加油后汽车行驶的速度为60千米/时
(D)加油后汽车行驶的速度比加油前汽车行驶的速度快
8. 张老师将自己2019年10月至2020年5月的通话时长(单位:分钟)的有关数据整理如下:
张老师将自己2019年10月至2020年5月的通话时长(单位:分钟)的有关数据整理如下:
①2019年10月至2020年3月通话时长统计表
时间 | 10月 | 11月 | 12月 | 1月 | 2月 | 3月 |
时长(单位:分钟) | 520 | 530 | 550 | 610 | 650 | 660 |
②2020年4月与2020年5月,这两个月通话时长的总和为1100分钟
根据以上信息,推断张老师这八个月的通话时长的中位数可能的最大值为
(A)550 (B)580 (C)610 (D)630
二、填空题(本题共16分,每小题2分)
9.若代数式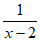 在实数范围内有意义,则
在实数范围内有意义,则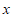 的取值范围是_______.
的取值范围是_______.
10.因式分解: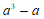 =_______.
=_______.
11.如图,D,E分别是△ABC的边AB,AC的中点,若△ADE的面积为1,则△ABC的面积等于______.
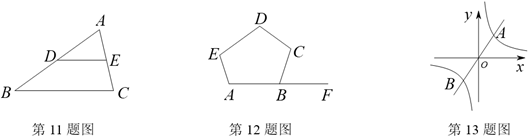
 12.如图,∠A=∠ABC=∠C=∠D=∠E,点F在AB的延长线上,则∠CBF的度数是__.
12.如图,∠A=∠ABC=∠C=∠D=∠E,点F在AB的延长线上,则∠CBF的度数是__.
13.如图,双曲线 与直线y=mx交于A,B两点,若点A的坐标为(2,3),则点B的坐标为_______.
与直线y=mx交于A,B两点,若点A的坐标为(2,3),则点B的坐标为_______.
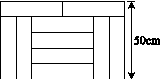
14.如图,用10个大小、形状完全相同的小矩形,拼成一个宽为50 cm的大矩形,设每个小矩形的长为 x cm,宽为y cm,则可以列出的方程组是______.
15.某调查机构对某地互联网行业从业情况进行调查统计,得到当地互联网行业从业人员年龄分布统计图和当地90后从事互联网行业岗位分布统计图:
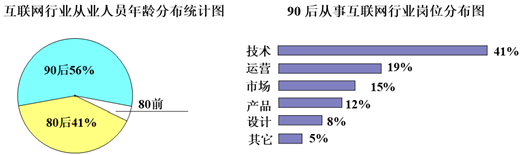
对于以下四种说法,你认为正确的是________ (写出全部正确说法的序号) .
① 在当地互联网行业从业人员中,90后人数占总人数的一半以上
② 在当地互联网行业从业人员中,80前人数占总人数的13%
③ 在当地互联网行业中,从事技术岗位的90后人数超过总人数的20%
④ 在当地互联网行业中,从事设计岗位的90后人数比80前人数少
16.一个袋中装有偶数个球,其中红球、黑球各占一半,甲、乙、丙是三个空盒.每次从袋中任意取出两个球,如果先放入甲盒的球是红球,则另一个球放入乙盒;如果先放入甲盒的球是黑球,则另一个球放入丙盒.重复上述过程,直到袋中所有的球都被放入盒中.
(1)某次从袋中任意取出两个球,若取出的球都没有放入丙盒,则先放入甲盒的球的颜色是____.
(2)若乙盒中最终有5个红球,则袋中原来最少有__个球.
三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27,28题,每小题7分)
解答应写出文字说明、演算步骤或证明过程.
17.计算: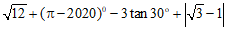 .
.
18.解方程: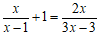 .
.
19.已知关于x的一元二次方程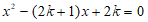 .
.
(1)求证:方程总有两个实数根;
(2)若该方程有一个根大于2,求k的取值范围.
20.下面是小明设计的”在已知三角形的一边上取一点,使得这点到这个三角形的另外两边的距离相等”的尺规作图过程:
已知:△ABC.
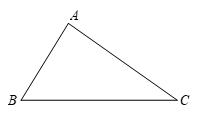
求作:点D,使得点D在BC边上,且到AB,AC边的距离相等.
作法:如图,
作∠BAC的平分线,交BC于点D.
则点D即为所求.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:作DE⊥AB于点E,作DF⊥AC于点F,
∵AD平分∠BAC,
∴ ________ =________ ( ) (填推理的依据) .
21.如图,在Rt△ABC中,∠ACB = 90°,D为AB的中点,AE∥DC,CE∥DA.
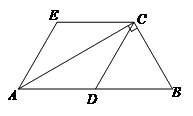
(1)求证:四边形ADCE是菱形;
(2)连接DE,若AC =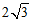 ,BC =2,
,BC =2,
求证:△ADE是等边三角形.
22. 某医院医生为了研究该院某种疾病的诊断情况,需要调查来院就诊的病人的两个生理指标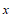 ,
, ,于是他分别在这种疾病的患者和非患者中,各随机选取20人作为调查对象,将收集到的数据整理后,绘制统计图如下:
,于是他分别在这种疾病的患者和非患者中,各随机选取20人作为调查对象,将收集到的数据整理后,绘制统计图如下:
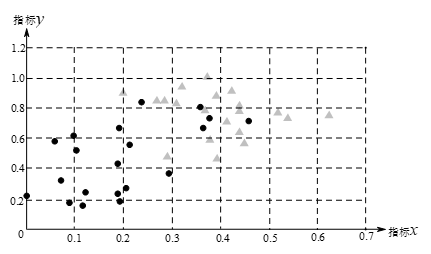
注”●”表示患者,”▲”表示非患者.
根据以上信息,回答下列问题:
(1)在这40名被调查者中,
①
指标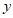 低于0.4的有______人;
低于0.4的有______人;
②将20名患者的指标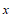 的平均数记作
的平均数记作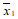 ,方差记作
,方差记作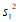 ,20名非患者的指标
,20名非患者的指标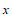 的
的
平均数记作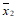 ,方差记作
,方差记作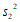 ,则
,则
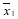 __
__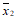 ,
,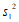 __
__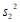 (填”>”,”=”或”<“) ;
(填”>”,”=”或”<“) ;
(2)来该院就诊的500名未患这种疾病的人中,估计指标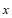 低于0.3的大约有____人;
低于0.3的大约有____人;
(3)若将”指标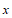 低于0.3,且指标
低于0.3,且指标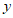 低于0.8″作为判断是否患有这种疾病的依据,则 发生漏判的概率是____.
低于0.8″作为判断是否患有这种疾病的依据,则 发生漏判的概率是____.
23. 如图,AB是⊙O的直径,C,D是⊙O 上两点,且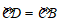 ,连接OC,BD,OD.
,连接OC,BD,OD.
(1)求证:OC垂直平分BD;
(2)过点C作⊙O的切线交AB的延长线于点E,连接AD,CD.
①依题意补全图形;
②若AD=6,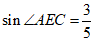 ,求CD的长.
,求CD的长.
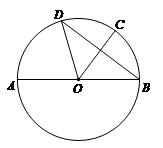
24.如图,在△ABC中,AE平分∠BAC交BC于点E,D是AB边上一动点,连接CD交AE于点P,连接BP.已知AB = 6 cm,设B,D两点间的距离为x cm,B,P两点间的距离为y1 cm,A,P两点间的距离为y2 cm.
小明根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,
分别得到了y1,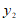 与x的几组对应值:
与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 2.49 | 2.64 | 2.88 | 3.25 | 3.80 | 4.65 | 6.00 |
y2/cm | 4.59 | 4.24 | 3.80 | 3.25 | 2.51 | 0.00 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,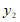 ),并画出函数y1,
),并画出函数y1,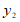 的图象;
的图象;
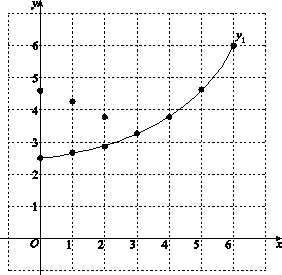
(3)结合函数图象,回答下列问题:
① 当AP=2BD时,AP的长度约为 ________cm;
② 当BP平分∠ABC时,BD的长度约为______cm.
25.在平面直角坐标系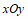 中,函数
中,函数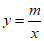 (
(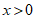 )的图象G与直线
)的图象G与直线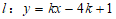 交于点A(4,1),点B(1,n)(n≥4,n为整数)在直线l上.
交于点A(4,1),点B(1,n)(n≥4,n为整数)在直线l上.
(1)求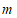 的值;
的值;
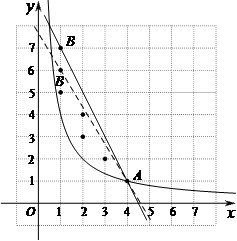
(2)横、纵坐标都是整数的点叫做整点.记图象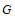 与直线l围成的区域(不含边界)为W.
与直线l围成的区域(不含边界)为W.
① 当 n = 5时,求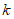 的值,并写出区域W内的整点个数;
的值,并写出区域W内的整点个数;
② 若区域W内恰有5个整点,结合函数图象,求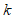 的取值范围.
的取值范围.
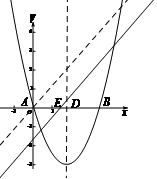
26. 在平面直角坐标系xOy中,抛物线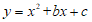 与x轴交于点A,B(A在B的左侧),抛物线的对称轴与x轴交于点D,且OB=2OD.
与x轴交于点A,B(A在B的左侧),抛物线的对称轴与x轴交于点D,且OB=2OD.
 (1)当
(1)当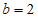 时,
时,
① 写出抛物线的对称轴;
② 求抛物线的表达式;
(2)存在垂直于x轴的直线分别与直线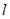 :
: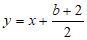 和抛物线交于点P,Q,且点P,Q均在x轴下方,结合函数图象,求b的取值范围.
和抛物线交于点P,Q,且点P,Q均在x轴下方,结合函数图象,求b的取值范围.
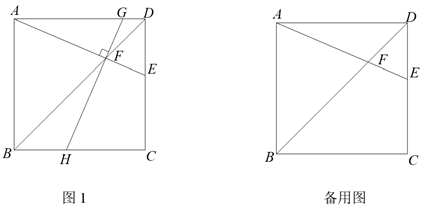
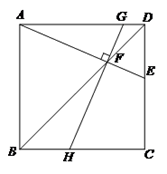
27. 在正方形ABCD中,E是CD边上一点(CE >DE),AE,BD交于点F.
(1)如图1,过点F作GH⊥AE,分别交边AD,BC于点G,H.
求证:∠EAB =∠GHC;
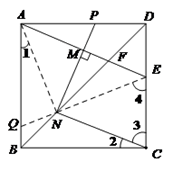
(2)AE的垂直平分线分别与AD, AE, BD交于点P,M,N,连接CN.
① 依题意补全图形;
②
用等式表示线段AE与CN之间的数量关系,并证明.
 28. 对于平面直角坐标系xOy中的定点P和图形F,给出如下定义:若在图形F上存在一点N,使得点Q,点P关于直线ON对称,则称点Q是点P关于图形F的定向对称点.
28. 对于平面直角坐标系xOy中的定点P和图形F,给出如下定义:若在图形F上存在一点N,使得点Q,点P关于直线ON对称,则称点Q是点P关于图形F的定向对称点.
(1)如图,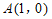 ,
,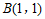 ,
,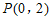 ,
,
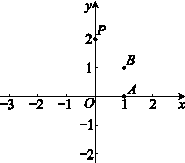
① 点P关于点B的定向对称点的坐标是______;
② 在点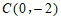 ,
,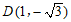 ,
,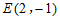 中,________是点P关于线段AB的定向对称点.
中,________是点P关于线段AB的定向对称点.
(2)直线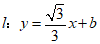 分别与x轴,y轴交于点G,H,⊙M是以点
分别与x轴,y轴交于点G,H,⊙M是以点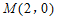 为圆心,
为圆心,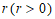 为半径的圆.
为半径的圆.
①当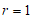 时,若⊙M上存在点K,使得它关于线段GH的定向对称点在线段GH上,求
时,若⊙M上存在点K,使得它关于线段GH的定向对称点在线段GH上,求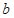 的取值范围;
的取值范围;
②对于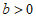 ,当
,当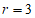 时,若线段GH上存在点J,使得它关于⊙M的定向对称点在⊙M上,直接写出b的取值范围.
时,若线段GH上存在点J,使得它关于⊙M的定向对称点在⊙M上,直接写出b的取值范围.
【试题答案】
一、选择题(本题共16分,每小题2分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | A | B | D | A | C | B | D | B |
二、填空题(本题共16分,每小题2分)
9.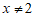 10.
10.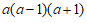 11.4
11.4
12.72°13.(-2,-3)14.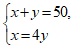
15.①③16.(1)红(2)20.
三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27,28题,每小题7分)
17.解: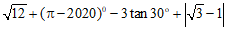
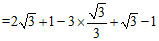
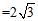 .5分
.5分
18.解:方程两边乘以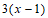 ,得
,得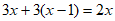 .
.
解得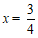 .
.
检验:当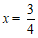 时,
时,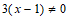 .
.
所以,原分式方程的解为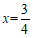 . 5分
. 5分
19.解:(1)依题意,得△=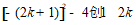 .
.
=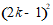 .
.
∵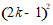 ≥
≥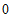 ,
,
∴方程总有两个实数根.
(2)解:由求根公式,得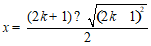 ,
,
∴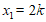 ,
,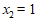 .
.
∵该方程有一个根大于2,
∴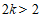 .
.
∴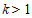 .
.
∴k的取值范围是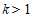 .5分
.5分
20.解:(1)如图.
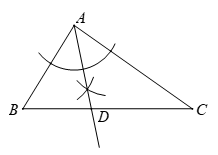
(2)DE,DF,角平分线上的点到角两边的距离相等. 5分
21.证明:(1)∵AE∥DC,CE∥DA,
∴四边形ADCE是平行四边形.
∵在Rt△ABC中,D为AB的中点,
∴AD=BD=CD=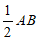 .
.
∴四边形ADCE是菱形.
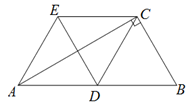
(2)在Rt△ABC中,AC=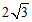 ,BC=2,
,BC=2,
∴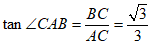 .
.
∴∠CAB=30°.
∵四边形ADCE是菱形.
∴AE=AD,∠EAD=2∠CAB=60°.
∴△ADE是等边三角形.5分
22.解:(1)①9.
②<,>.
(2)100.
(3)0.25. 5分
23.(1)证明:∵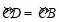
∴∠COD=∠COB.
∵OD=OB,
∴OC垂直平分BD.
(2)解:①补全图形,如图所示.
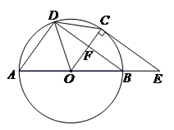
②∵CE是⊙O切线,切点为C,
∴OC⊥CE于点C.
记OC与BD交于点F,由(1)可知OC垂直BD,
∴∠OCE=∠OFB=90°.
∴DB∥CE.
∴∠AEC=∠ABD.
在Rt△ABD中,AD=6,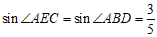 ,
,
∴BD=8,AB=10.
∴OA=OB=OC=5.
由(1)可知OC平分BD,即DF=BF,
∴BF=DF=4.
∴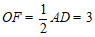 .
.
∴CF=2.
在Rt△CFD中,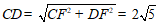 . 6分
. 6分
24.解:(1)
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| |||||||
| 1.50 |
(2)画出函数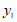 的图象;
的图象;
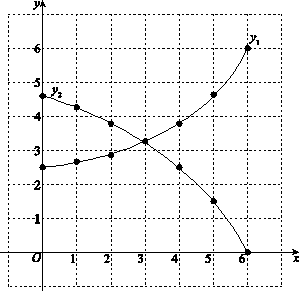
(3)答案不唯一,如:
①3.86;
②3.6分
25.解:(1)∵点A(4,1)在函数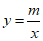 (
(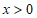 )的图象G上,
)的图象G上,
∴m=4.
(2)①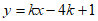 ,经过点B(1,5),
,经过点B(1,5),
∴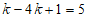 .
.
解得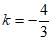 .
.
此时区域 内有2个整点.
内有2个整点.
②∵直线l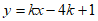
过定点A(4,1),
∵n为整数,
当n=6时,直线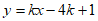 ,经过点B(1,6),区域
,经过点B(1,6),区域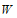 内有4个整点,
内有4个整点,
当n=7时,直线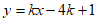 ,经过点B(1,7),区域
,经过点B(1,7),区域 内有5个整点,
内有5个整点,
此时,可得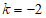 .
.
当n≥8时,区域 内的整点个数大于5个.
内的整点个数大于5个.
∴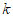 的取值范围是
的取值范围是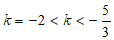 .6分
.6分
26.解:(1)当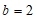 时,
时,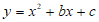 化为
化为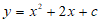 .
.
①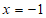 .
.
②∵抛物线的对称轴为直线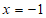 ,
,
∴点D的坐标为(-1,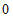 ),OD=1.
),OD=1.
∵OB=2OD,
∴OB=2.
∵点A,点B关于直线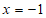 对称,
对称,
∴点B在点D的右侧.
∴点B的坐标为(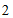 ,
,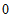 ).
).
∵抛物线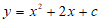 与x轴交于点B(
与x轴交于点B(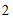 ,
,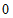 ),
),
∴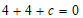 .
.
解得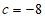 .
.
∴抛物线的表达式为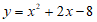 .
.
(2)设直线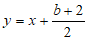 与x轴交点为点E,
与x轴交点为点E,
∴E(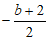 ,0).
,0).
抛物线的对称轴为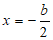 ,
,
∴点D的坐标为(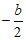 ,
,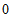 ).
).
①当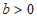 时,
时,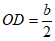 .
.
∵OB=2OD,
∴OB=b.
∴点A的坐标为(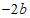 ,
,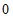 ),点B的坐标为(b,
),点B的坐标为(b,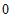 ).
).
当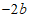 <
<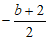 时,存在垂直于x轴的直线分别与直线
时,存在垂直于x轴的直线分别与直线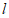 :
: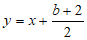
和抛物线交于点P,Q,且点P,Q均在x轴下方,
解得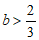 .
.
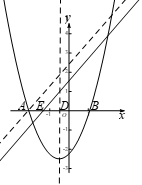
②当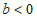 时,
时,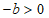 .
.
∴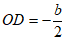 .
.
∵OB=2OD,
∴OB=-b.
∵抛物线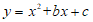 与x轴交于点A,B,且A在B的左侧,
与x轴交于点A,B,且A在B的左侧,
∴点A的坐标为(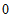 ,
,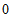 ),点B的坐标为(-b,
),点B的坐标为(-b,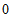 ).
).
当0<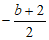 时,存在垂直于x轴的直线分别与直线
时,存在垂直于x轴的直线分别与直线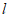 :
: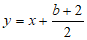
和抛物线交于点P,Q,且点P,Q均在x轴下方,
解得b<-2.
综上,b的取值范围是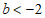 或
或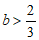 .6分
.6分
27.(1)证明:在正方形ABCD中,AD∥BC,∠BAD=90°,
∴∠AGH=∠GHC.
∵GH⊥AE,
∴∠EAB=∠AGH.
∴∠EAB=∠GHC.
(2)①补全图形,如图所示.
②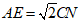 .
.
证明:连接AN,连接EN并延长,交AB边于点Q.
∵四边形ABCD是正方形,
∴点A,点C关于BD对称.
∴NA=NC,∠1=∠2.
∵PN垂直平分AE,
∴NA=NE.
∴NC=NE.
∴∠3=∠4.
在正方形ABCD中,BA∥CE,∠BCD=90°,
∴∠AQE=∠4.
∴∠1+∠AQE=∠2+∠3=90°.
∴∠ANE=∠ANQ=90°.
在Rt△ANE中,
∴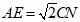 .7分
.7分
28.解:(1)①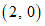 ;
;
②C,D.
(2)①由题意,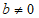 ,
,
若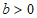 ,
,
当直线l与以点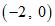 为圆心,1为半径的圆相切时,
为圆心,1为半径的圆相切时,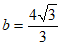 .
.
当直线l经过点 时,
时,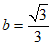 .
.
∴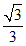 ≤
≤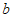 ≤
≤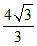 .
.
若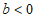 ,
,
当直线l经过点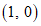 时,
时,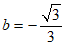 .
.
当直线l与以点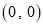 为圆心,3为半径的圆相切时,
为圆心,3为半径的圆相切时,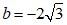 .
.
∴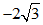 ≤
≤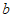 ≤
≤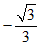 .
.
综上,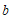 的取值范围是
的取值范围是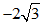 ≤
≤ ≤
≤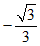 或
或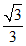 ≤
≤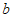 ≤
≤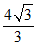 .
.
②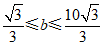 .7分
.7分

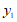 /cm
/cm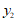 /cm
/cm