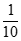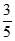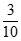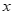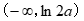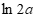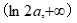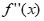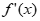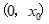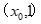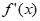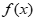一、选择题共10小题。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 设集合A={x∈Z|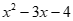 ≤0},B={x|
≤0},B={x|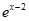 <1},则A
<1},则A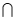 B=(
B=(
)
A. {-1,0,l,2} B. [-1,2) C. {-1,0,1} D. [-1,2]
2. 已知复数z=2+i,则z·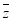 =(
=(
)
A. 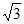 B.
B. 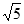 C. 3 D. 5
C. 3 D. 5
3. 下列函数中既是奇函数,又在区间(0,1)上单调递减的是(
)
A. 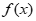 =
=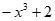 B.
B.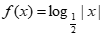
C. 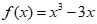 D.
D. 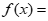 sinx
sinx
4. 设抛物线C: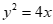 上一点P到y轴的距离为4,则点P到抛物线C的焦点的距离是(
上一点P到y轴的距离为4,则点P到抛物线C的焦点的距离是(
)
A. 4 B. 5 C. 6 D. 7
5. 某公司一年需要购买某种货物4800吨,每次购买x吨,运费为3万元/次,一年的总存储费用为4x万元。要使一年的总运费与总存储费用之和最小,则x的值是(
)
A. 20 B. 30 C. 45 D. 60
6. 已知角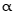 以x轴正半轴为始边,其终边在射线
以x轴正半轴为始边,其终边在射线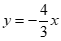 (x≤0)上,则sin
(x≤0)上,则sin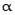 +cos
+cos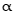 =(
=(
)
A. –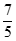 B. –
B. –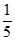 C.
C. 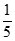 D.
D.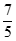
7. 如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该多面体的体积为(
)
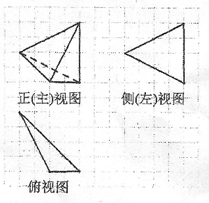
A. 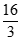 B.
B. 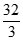 C.
C. 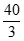 D. 16
D. 16
8.在△ABC中,若a=9,b=6,A=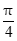 ,则cos B=(
,则cos B=(
)
A. 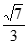 B.
B. 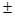
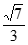 C.
C. 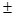
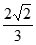 D.
D.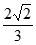
9. 已知△ABC,则“sinA=COS B”是“△ABC是直角三角形“的(
)
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
10.若无穷数列{an}满足:a1≥0,当n∈N*,n≥2时,|an-an-1|=max{a1,a2,…,an-1}(其中max{a1,a2,…,an-1}表示a1,a2,…,an-1中的最大项),则以下结论:
①若数列{an}是常数列,则an=0(n∈N*);
②若数列{an}是公差d≠0的等差数列,则d<0:
③若数列{an}是公比为q的等比数列,则q>l;
④若存在正整数T,对任意n∈N*,都有an+T=an,则a1是数列{an}的最大项。
所有正确的结论是(
)
A. ①② B. ②③ C. ①②③ D. ①②③④
二、填空题共5小题。
11. 已知非零向量a,b的夹角为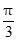 ,且(a-b)⊥b,则
,且(a-b)⊥b,则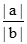 =________。
=________。
12.已知a>0,b>0,若(ax2+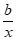 )8的展开式中x4项的系数为70,则ab的值为________。
)8的展开式中x4项的系数为70,则ab的值为________。
13.已知圆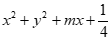 =0与双曲线
=0与双曲线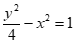 的渐近线相切,则m的值为________。
的渐近线相切,则m的值为________。
14.已知点M(1,0),N(0,-1),若点P在函数y=ln(x+2)的图像上,则使得△PMN面积为1的点P的个数为________。
15. 定义:若存在常数k,使得对定义域D内的任意两个x1,x2
(x1≠x2),均有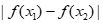
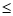
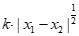 成立,则称函数
成立,则称函数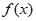 在定义域D上满足
在定义域D上满足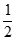 阶H
阶H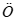 LDER条件。
LDER条件。
(1)函数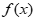 =2x是否满足
=2x是否满足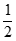 阶H
阶H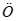 LDER条件?___________(填“是”或“否“);
LDER条件?___________(填“是”或“否“);
(2)已知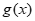 =
=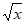 (x≥0)满足
(x≥0)满足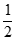 阶H
阶H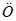 LDER条件,则常数k的最小值为________。
LDER条件,则常数k的最小值为________。
三、解答题共6小题。解答应写出文字说明、演算步骤或证明过程。
16. 已知{an}是公比为q的无穷等比数列,其前n项和为Sn,满足a2=6,_________,是否存在正整数k,使得Sk>1000?若存在,求k的最小值;若不存在,说明理由。
从①S3=21;②a4=24;③a5=48这三个条件中任选一个,补充在上面问题中并作答。
17.体温是人体健康状况的直接反应,一般认为成年人腋下温度T(单位:℃)平均在36℃~37℃之间即为正常体温,超过37.1℃即为发热。发热状态下,不同体温可分成以下三种发热类型:低热:37.1≤T≤38;高热:38<T≤40;超高热(有生命危险):T>40。某位患者因患肺炎发热,于12日至26日住院治疗。医生根据病情变化,从14日开始,以3天为一个疗程,分别用三种不同的抗生素为该患者进行消炎退热。住院期间,患者每天上午8:00服药,护士每天下午4:00为患者测量腋下体温记录如下:
抗生素使用情况 | 没有使用 | 使用”抗生素A“治疗 | 使用”抗生素B”治疗 | |||||
日期 | 12日 | 13日 | 14日 | 15日 | 16日 | 17日 | 18日 | 19日 |
体温(℃) | 38.7 | 39.7 | 39.7 | 40.1 | 39.9 | 39.2 | 38.9 | 39.0 |
抗生素使用情况 | 使用”抗生素C”治疗 | 没有使用 | |||||
日期 | 20日 | 21日 | 22日 | 23日 | 24日 | 25日 | 26日 |
体温(℃) | 38.4 | 38.0 | 37.6 | 37.1 | 36.8 | 36.6 | 36.3 |
(1)请你计算住院期间该患者体温不低于39℃的各天体温平均值;
(2)在19日~23日这5天中,医生会随机选取3天在测量体温的同时为该患者进行某一特殊项目” 项目“的检查,记X为高热体温下做“
项目“的检查,记X为高热体温下做“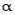 项目“检查的天数,试求X的分布列与数学期望:
项目“检查的天数,试求X的分布列与数学期望:
(3)抗生素治疗一般在服药后2-8个小时就能出现血液浓度的高峰,开始杀灭细菌,达到消炎退热效果。假设三种抗生素治疗效果相互独立,请依据表中数据,判断哪种抗生素治疗效果最佳,并说明理由。
18.如图1,△DAC和△ABC都是等腰直角三角形,其中AB=BC,AC=CD=2。现将△DAC沿AC折起到△VAC的位置,如图2,M为VA的中点,过CM的平面CMN与直线AB平行,且与直线VB交于点N。
(1)求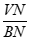 的值;
的值;
(2)当平面VAC⊥平面ABC时,
①求直线VB与平面MBC所成角的正弦值;
②在平面VAC内是否存在一点P,使得NP⊥平面MBC?若存在,求线段CP的长度;若不存在,说明理由。
19. 已知椭圆C: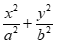 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为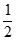 ,过椭圆右焦点F的直线l与椭圆交于A,B两点,当直线l与x轴垂直时,|AB|=3。
,过椭圆右焦点F的直线l与椭圆交于A,B两点,当直线l与x轴垂直时,|AB|=3。
(1)求椭圆C的标准方程;
(2)当直线l与x轴不垂直时,在x轴上是否存在一点P(异于点F),使x轴上任意点到直线PA,PB的距离均相等?若存在,求P点坐标;若不存在,请说明理由。
20. 已知函数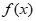 =
=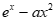 (a∈R)。
(a∈R)。
(1)若曲线y=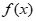 在(1,f(1))处的切线与x轴平行,求a;
在(1,f(1))处的切线与x轴平行,求a;
(2)已知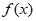 在[0,1]上的最大值不小于2,求a的取值范围;
在[0,1]上的最大值不小于2,求a的取值范围;
(3)写出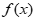 所有可能的零点个数及相应的a的取值范围。(请直接写出结论)
所有可能的零点个数及相应的a的取值范围。(请直接写出结论)
21. 对于无穷数列{cn},若对任意m,n∈N*,且m≠n,存在k∈N*,使得cm+cn=ck成立,则称{cn}为“G数列“。
(1)若数列{bn}的通项公式为bn=2n,{tn}的通项公式为tn=2n+1,分别判断{bn},{tn}是否为“G数列“,并说明理由;
(2)已知数列{an}为等差数列,
①若{an}是“G数列“,a1=8,a2∈N*,且a2> a1,求a2所有可能的取值;
②若对任意n∈N*,存在k∈N*,使得ak=Sn成立,求证:数列{an}为“G数列“。
参考答案
1. C 2. D 3. C 4. B 5. D 6. C 7. A 8. A 9. D 10. D
11.2. 12.1. 13.±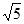 . 14.3. 15.(1)否;(2)1.
. 14.3. 15.(1)否;(2)1.
16.选择①,因为a2=6,S3=21,所以q≠1。
所以S3=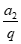 +a2+ a2q=
+a2+ a2q=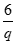 +6+6q=21。所以q=2或q=
+6+6q=21。所以q=2或q=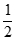 。
。
当q=2时,a1=3,Sn=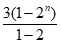 =3(2n-1),
=3(2n-1),
令Sk>1000,即2k>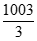 ,所以使得Sk>1000的正整数k的最小值为9。
,所以使得Sk>1000的正整数k的最小值为9。
当q=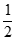 时,a1=12,Sn=
时,a1=12,Sn=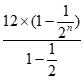 =24(1-
=24(1-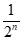 )
)
令Sk>1000,即2k<-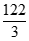 ,所以不存在满足条件的正整数k。
,所以不存在满足条件的正整数k。
选择②,因为a2=6,a4=24,所以q=±2。
当q=2时,a1=3,Sn=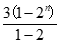 =3(2n-1),
=3(2n-1),
令Sk>1000,即2k>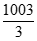 ,所以使得Sk>1000的正整数k的最小值为9。
,所以使得Sk>1000的正整数k的最小值为9。
当q=-2时,a1=-3,所以Sn=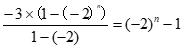 ,
,
令Sk>1000,即(-2)k>1001。
当k为偶数时,2k>1001,所以正整数k的最小值为10。
当k为奇数时,原不等式无解;
所以使得Sk>2020的正整数k的最小值为10。
选择③,因为a2=6,a5=48,所以q3=8。
所以q=2,a1=3,Sn=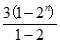 =3(2n-1),
=3(2n-1),
令Sk>1000,即2k>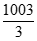 。
。
所以使得Sk>1000的正整数k的最小值为9。
17.(1)由表可知,该患者共6天的体温不低于39℃,记平均体温为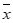 ,
,
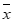 =
=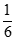 (39.4+39.7+40.1+39.9+39.2+39.0)=39.55℃。
(39.4+39.7+40.1+39.9+39.2+39.0)=39.55℃。
所以,患者体温不低于39℃的各天体温平均值为39.55℃。
(2)X的所有可能取值为0,1,2。
P(X=0)=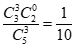 ,P(X=1)=
,P(X=1)= 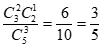 ,P(X=2)=
,P(X=2)= 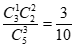 。
。
则X的分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
所以E(X)=0×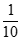 +1×
+1×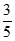 +2×
+2×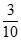 =
=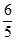 。
。
(3)“抗生素C”治疗效果最佳可使用理由:
①“抗生素B”使用期间先连续两天降温1.0℃又回升0.1℃,“抗生素C”使用期间持续降温共计1.4℃,说明“抗生素C”降温效果最好,故“抗生素C”治疗效果最佳。
②“抗生素B”治疗期间平均体温39.03℃,方差约为0.0156;“抗生素C”平均体温38℃,方差约为0.1067,“抗生素C”治疗期间体温离散程度大,说明存在某个时间节点降温效果明显,故“抗生素C”治疗效果最佳。
“抗生素B”治疗效果最佳可使用理由:
自使用“抗生素B”开始治疗后,体温才开始稳定下降,且使用“抗生素B”治疗当天共降温0.7℃,是单日降温效果最好的一天,故“抗生素B”治疗效果最佳。
18.(1)因为AB∥平面CMN,平面CMN 平面VAB=MN,
平面VAB=MN,
所以AB∥MN。
因为M为VA的中点,所以N为VB的中点,所以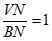 。
。
(2)①在等腰直角三角形VAC中,
因为AC=VC=2,所以VC⊥AC。
又平面VAC⊥平面ABC,
平面VAC 平面ABC=AC,
平面ABC=AC,
所以VC⊥平面ABC。
在平面ABC内过点C做y轴垂直于AC,
则VC⊥y轴,VC⊥AC,
如图建立空间直角坐标系C-xyz。
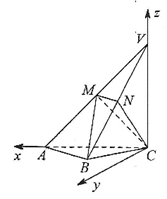
则C(0,0,0),V(0,0,2),B(1,1,0),M(1,0,1),
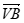 =(1,1,-2),
=(1,1,-2),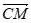 =(1,0,1),
=(1,0,1),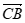 =(1,1,0)。
=(1,1,0)。
设平面MBC的法向量为n=(x,y,z),
则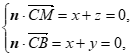 令x=1,则y=-1,z=-1所以n=(1,-1,-1)。
令x=1,则y=-1,z=-1所以n=(1,-1,-1)。
设直线VB与平面MBC所成角为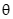 ,
,
则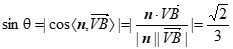
②若在平面VAC内存在一点P,NP⊥平面MBC,
设P(x0,0,z0),则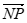 ∥n,
∥n,
因为N(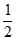 ,
,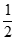 ,1),所以
,1),所以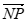 =(x0–
=(x0–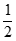 ,–
,–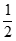 ,z0-1),
,z0-1),
所以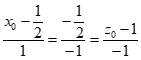 ,所以
,所以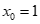 ,
,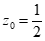 ,
,
所以,存在点P(1,0,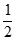 ),CP=
),CP=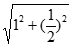 =
=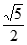 。
。
19.(1)由题意得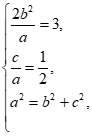 解得:a=2,b=
解得:a=2,b=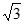 ,c=1。
,c=1。
所以椭圆的标准方程为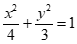 。
。
(2)依题意,若直线l的斜率不为零,可设直线l:x=my+1(m≠0),A(x1,y1),B(x2,y2)。
假设存在点P,设P(x0,0),由题设,x0≠1,且x0≠x1,x0≠x2。
设直线PA,PB的斜率分别为k1,k2,则k1=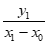 ,k2=
,k2=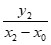 。
。
因为A(x1,y1),B(x2,y2)在x=my+1上,故x1=my1+1,x2=my2+1。
而x轴上任意点到直线PA,PB距离均相等等价于“PF平分∠APB”,
继而等价于k1+k2=0。
则k1+k2=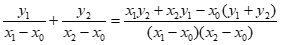
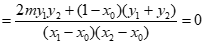 。
。
联立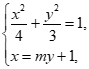 消去x,得(3m2+4)y2+6my-9=0,
消去x,得(3m2+4)y2+6my-9=0,
有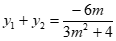 ,
,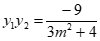 。
。
则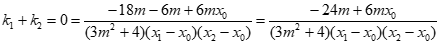
即-4m+mx0=0,故x0=4或m=0(舍)。
当直线l的斜率为零时,P(4,0)也符合题意。
故存在点P(4,0),使得x轴上任意点到直线PA,PB距离均相等。
20.(1)因为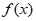 =
=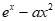 (a∈R),所以
(a∈R),所以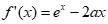 。
。
依题意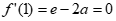 ,即
,即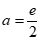 。
。
当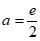 时,
时,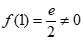 ,此时切线不与x轴重合,符合题意,因此
,此时切线不与x轴重合,符合题意,因此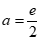 。
。
(2)由(1)知,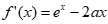 ,
,
当a≤0时,因为x∈[0,1],ex>0,-2ax≥0,
故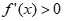 ,即
,即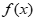 单增,因此
单增,因此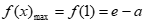 。
。
依题意,当a≤0时,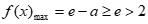 ,所以a≤0符合题意。
,所以a≤0符合题意。
当a>0时,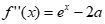 ,
,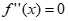 ,有x=ln2a。
,有x=ln2a。
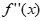 ,
,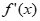 变化如下:
变化如下:
|
|
|
|
| – | 0 | + |
| ↘ | 极小值 | ↗ |
故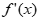 min=2a-2aln2a=2a(1-ln2a)。
min=2a-2aln2a=2a(1-ln2a)。
当1-ln2a≥0时,即0<a≤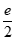 时,
时,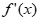 ≥0,
≥0,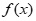 单调递增,
单调递增,
因此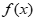 max=
max=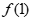 =e–a。
=e–a。
依题意,令e–a≥2,有0<a≤e-2。
当1-ln 2a<0时,即a>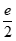 时,
时,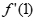 =e-2a<0,
=e-2a<0,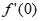 =1>0,
=1>0,
故存在唯一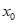 ∈(0,1)使
∈(0,1)使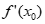 =0。
=0。
此时有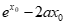 =0,即
=0,即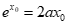 ,
,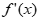 ,
,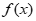 变化如下:
变化如下:
|
|
|
|
| + | 0 | – |
| ↗ | 极大值 | ↘ |
所以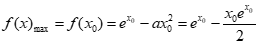 ,x0∈(0,1)。
,x0∈(0,1)。
依题意,令g(x)=ex–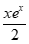 ,x∈(0,1),则
,x∈(0,1),则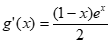 >0,g(x)在(0,1)单调递增,
>0,g(x)在(0,1)单调递增,
所以g(x)<g(1)=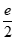 <2,所以
<2,所以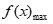 <2,此时不存在符合题意的a。
<2,此时不存在符合题意的a。
综上所述,当a∈(–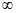 ,e-2],
,e-2],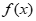 在[0,1]上的最大值不小于2,
在[0,1]上的最大值不小于2,
若a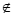 (–
(–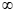 ,e-2],则
,e-2],则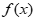 在[0,1]上的最大值小于2,
在[0,1]上的最大值小于2,
所以a的取值范围为(–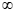 ,e-2]。
,e-2]。
方法二:
(2)当x∈[0,1]时,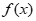 最大值不小于2,等价于
最大值不小于2,等价于
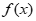 =
=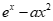 ≥2在x∈[0,1]上有解,显然x=0不是解,
≥2在x∈[0,1]上有解,显然x=0不是解,
即a≤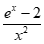 在x∈(0,1]上有解,
在x∈(0,1]上有解,
设g(x)=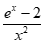 ,x∈(0,1],则
,x∈(0,1],则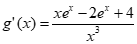 。
。
设h(x)=xex-2ex+4,x∈(0,1],则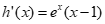 ≤0。
≤0。
所以h(x)在(0,1]单调递减,h(x)≥h(1)=4-e>0,
所以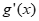 >0,所以
>0,所以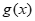 在(0,1]上单调递增,所以
在(0,1]上单调递增,所以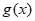 max=g(1)=e-2。
max=g(1)=e-2。
依题意需a≤e-2,所以a的取值范围为(–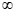 ,e-2]。
,e-2]。
方法三:
(2)由(1)知,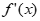 =ex-2ax,
=ex-2ax,
当a≤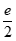 时,
时,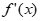 = ex-2ax≥ex–ex,
= ex-2ax≥ex–ex,
设h(x)= ex–ex,x∈[0,1],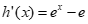 ≤0,
≤0,
所以h(x)在[0,1]单调递减,故h(x)≥h(1)=0。
所以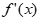 ≥0,所以
≥0,所以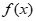 在[0,1]单调递增,
在[0,1]单调递增,
因此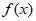 max=f(1)=e–a。
max=f(1)=e–a。
依题意,令e-a≥2,得a≤e-2。
当a>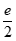 时,
时,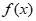 =ex–ax2≤ex–
=ex–ax2≤ex–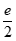 x2,
x2,
设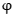 (x)= ex–
(x)= ex–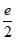 x2,x∈[0,1],则
x2,x∈[0,1],则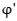 (x)=ex–ex=h(x)≥0,
(x)=ex–ex=h(x)≥0,
所以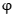 (x)在[0,1]单调递增,
(x)在[0,1]单调递增,
故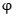 (x)max=
(x)max=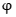 (1)=e-
(1)=e-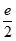 =
=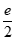 <2,即
<2,即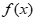 <2,不符合题意。
<2,不符合题意。
综上所述,a的取值范围为(–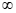 ,e-2]。
,e-2]。
(3)当a≤0时,y=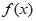 有0个零点;当0<a<
有0个零点;当0<a<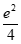 时,y=
时,y=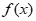 有1个零点;
有1个零点;
当a=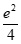 时,y=
时,y=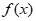 有2个零点;当a>
有2个零点;当a>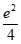 时,y=
时,y=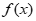 有3个零点。
有3个零点。
21. (1){bn}是“G数列“,理由是:
对任意m,n∈N*,且m≠n,bm=2m,bn=2n,bm+bn=2(m+n)=bm+n,m+n∈N*,
bm+n为数列{bn}中的第(m+n)项。
②数列{tn}不是“G数列“,理由是:
因为tn=2n+1,所以{tn}的每一项均为奇数,
因为t1+ t2=3+5=8为偶数,不是(tn)中的项,即不存在k∈N*,使得t1+ t2= tk。
(2)①因为{an}为等差数列,且a1=8,an=8+(n-1)(a2-8)。
若{an}是“G数列“,则对任意m,n∈N*且m≠n,存在k∈N*,使得am+an=ak成立,
即8+(m-1)(a2-8)+8+(n-1)( a2-8)=8+(k-1)(a2-8),
又因为a2> a1,所以k=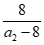 +m+n-1,
+m+n-1,
因为k∈N*,且a2>8,则a2-8=1,2,4,8。
所以a2=9,10,12,16。
②根据条件,对任意n∈N*,存在k∈N*,使得ak=Sn成立,
即na1+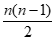 d= a1+(k-1)d。
d= a1+(k-1)d。
当d=0时,必有a1=0,此时数列{an}为“G数列“。
当d≠0时,对任意n∈N*,k=1+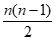 +(n-1)
+(n-1)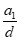 ∈N*,
∈N*,
取n=2,k=2+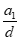 ∈N*,此时
∈N*,此时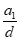 只可能取不小于-1的整数。
只可能取不小于-1的整数。
(A)当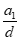 =-1时,k=1+
=-1时,k=1+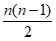 –(n-1)=
–(n-1)=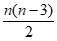 +2,
+2,
当n=1,2,3时,k分别取值1,1,2,均为正整数;
当n>3,n∈N*时,n与n-3的奇偶性不同,
则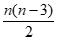 ∈N*,所以k=
∈N*,所以k=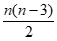 +2也为正整数。
+2也为正整数。
(B)当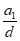 ∈N时,显然k=1+
∈N时,显然k=1+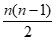 +(n-1)
+(n-1)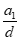 ∈N*。
∈N*。
令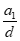 =s,则s的取值范围为{s∈Z|s≥-1}。
=s,则s的取值范围为{s∈Z|s≥-1}。
因为a1=sd,所以an=sd+(n-1)d=(s+n-1)d。
若对任意m,n∈N*且m≠n,有m+n≥3,
又因为s≥-1且S∈Z,所以r=s+m+n-1必为正整数。
因为am+ an=(s+m-1)d+(s+n-1)d=(2s+m+n-2)d,ar= as+m+n-1=(2s+m+n-2)d,
所以am+ an=ar,即对任意m,n∈N*且m≠n,存在r=s+m+n-1∈N*,使得am+an=ar。
所以当d≠0时,{an}为“G数列“。
综上所述,{an}为“G数列“。