本试卷共150分。考试时长120分钟。
第一部分
(选择题
共50分)
一、选择题共10小题,每小题5分,共50分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 下列各角中,与27°角终边相同的是
A. 63° B. 153° C. 207° D. 387°
2. 圆柱的母线长为5cm,底面半径为2cm,则圆柱的侧面积为
A. 20 πcm2 B. 10 πcm2 C. 28 πcm2 D. 14 πcm2
3. sin(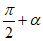 )=
)=
A. sin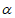 B. cos
B. cos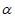 C. -sin
C. -sin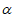 D. -cos
D. -cos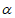
4. 设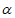 ∈(-π,π),且cos
∈(-π,π),且cos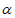 =-
=-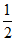 ,则
,则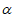 =
=
A. –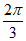 或
或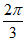 B. –
B. –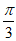 或
或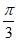
C. –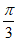 或
或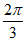 D. –
D. –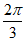 或
或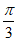
5. 设a,b均为单位向量,且a·b=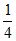 ,则|a+2b|=
,则|a+2b|=
A. 3 B. 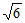 C. 6 D. 9
C. 6 D. 9
6. 下列四个函数中,以π为最小正周期,且在区间(0,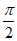 )上为增函数的是
)上为增函数的是
A. y=sin2x B. y=cos2x
C. y=tanx D. y=sin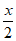
7. 向量a,b在正方形网格中的位置如图所示,则<a,b>=
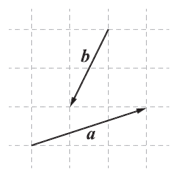
A. 45° B. 60° C. 120° D. 135°
8. 设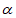 ,
,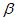 ∈(0,π),且
∈(0,π),且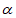 >
>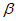 ,则下列不等关系中一定成立的是
,则下列不等关系中一定成立的是
A. sin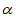 <sin
<sin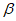 B. sin
B. sin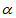 >sin
>sin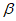
C. cos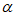 <cos
<cos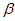 D. cos
D. cos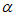 >cos
>cos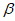
9. 将函数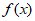 =sin2x的图像向右平移φ(0<φ≤
=sin2x的图像向右平移φ(0<φ≤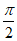 )个单位,得到函数
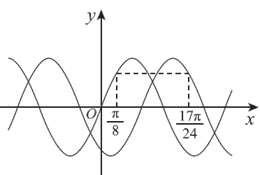
)个单位,得到函数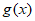 的图像。在同一坐标系中,这两个函数的部分图像如图所示,则φ=
的图像。在同一坐标系中,这两个函数的部分图像如图所示,则φ=
A. 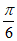 B.
B. 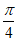 C.
C. 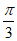 D.
D.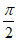
10. 棱锥被平行于底面的平面所截, 得到一个小棱锥和一个棱台。小棱锥的体积记为y,棱台的体积记为x,则y 与x 的函数图像为

A B C D
第二部分
(非选择题
共100分)
二、填空题共6小题,每小题4分,共24分。
11. 已知圆的半径为2,则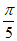 的圆心角所对的弧长为____。
的圆心角所对的弧长为____。
12. 在平面直角坐标系xOy中,角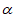 与角
与角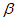 均以Ox为始边,它们的终边关于x轴对称。若sin
均以Ox为始边,它们的终边关于x轴对称。若sin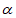 =
=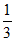 ,则sin
,则sin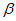 =____。
=____。
13. 向量a,b满足|b|=1,a·b=1。若 (λa–b)⊥b,则实数λ=____。
14. 已知正方体ABCD-A1B1C1D1的八个顶点在同一个球面上。若正方体的棱长是2,则球的直径是________;球的表面积是____。
15 已知函数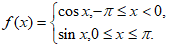 给出下列三个结论:
给出下列三个结论:
①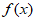 是偶函数;
是偶函数;
②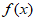 有且仅有3个零点;
有且仅有3个零点;
③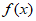 的值域是[-1,1]。
的值域是[-1,1]。
其中,正确结论的序号是____。
16. 设函数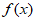 =sin(ωx+
=sin(ωx+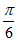 )(ω>0)。若
)(ω>0)。若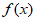 ≥
≥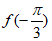 对任意的实数x都成立,则ω的最小值为______。
对任意的实数x都成立,则ω的最小值为______。
三、解答题共6小题,共76分。解答应写出文字说明,演算步骤或证明过程。
17. (本小题12分)
已知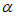 ∈(0,
∈(0,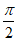 ),且cos
),且cos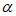 =
=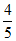 。
。
(Ⅰ)求tan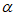 的值;
的值;
(Ⅱ)求sin2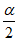 +sin2
+sin2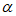 的值。
的值。
18. (本小题13分)
如图,正三棱锥P-ABC的底面边长为2,侧棱长为3。
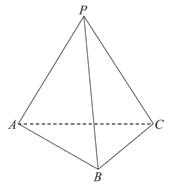
(Ⅰ)求正三棱锥P-ABC的表面积;
(Ⅱ)求正三棱锥P-ABC的体积。
19. (本小题12分)
在△ABC中,角A,B,C所对的边分别为a,b,c。C=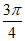 ,sinA=
,sinA=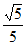 。
。
(Ⅰ)求sinB的值;
(Ⅱ)若c–a=5-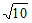 ,求△ABC的面积。
,求△ABC的面积。
20. (本小题14分)
已知函数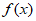 =
=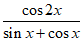 。
。
(Ⅰ)求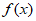 的定义域;
的定义域;
(Ⅱ)求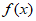 在区间[0,
在区间[0,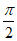 ]上的最大值;
]上的最大值;
(Ⅲ)求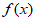 的单调递减区间。
的单调递减区间。
21. (本小题12分)
如图,在正方体ABCD-A1B1C1D1中,E为CC1的中点。
(Ⅰ)在图中作出平面AD1E和底面ABCD的交线,并说明理由;
(Ⅱ)平面AD1E将正方体分成两部分,求这两部分的体积之比。
22. (本小题13分)
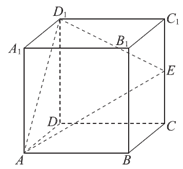
如图,在扇形OAB中,∠AOB=120°,半径OA=OB=2,P为弧AB上一点。
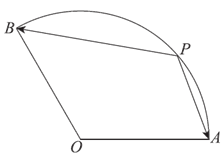
(Ⅰ)若OA⊥OP,求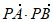 的值;
的值;
(Ⅱ)求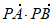 的最小值。
的最小值。
参考答案
一、选择题(共10小题,每小题5分,共50分)
1. D 2. A 3. B 4. A 5. B 6. C 7. D 8. C 9. C 10. A
二、填空题(共6小题,每小题4分,共24分)
11. 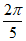 12. –
12. –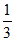
13. 1 14. 2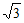 ;12π
;12π
15. ②③ 16. 2
注:(14)题每空2分;(15)题少解给2分,有错解不给分。
三、解答题(共6小题,共76分)
17. (共12分)
解:(Ⅰ)因为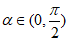 ,cos
,cos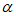 =
=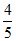 ,
,
所以sin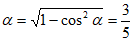 … 3分
… 3分
所以tan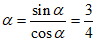 ……… 6分
……… 6分
(Ⅱ)因为sin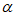 =
=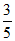 ,cos
,cos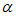 =
=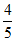 ,
,
所以sin2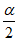 +sin2
+sin2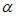 =
=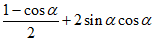 ……… 10 分
……… 10 分
=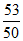 …… 12 分
…… 12 分
18.(共13分)
解:(Ⅰ)取BC的中点D,连接PD。
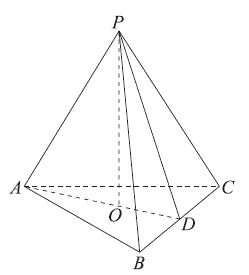
在Rt△PBD中,PD=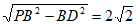 ,………1 分
,………1 分
所以S△PBC=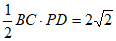 。 ………3 分
。 ………3 分
因为正三棱锥的三个侧面是全等的等腰三角形,
所以正三棱锥P-ABC的侧面积是3S△PBC= 6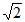 。…… 5 分
。…… 5 分
因为正三棱锥的底面是边长为2的正三角形,
所以正三棱锥P-ABC的底面积为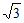 ,…… 7分
,…… 7分
所以正三棱锥P-ABC的表面积为6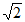 +
+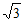 。 …… 8 分
。 …… 8 分
(Ⅱ)连接AD,设点O是正△ABC的中心,则PO垂直于底面ABC,
且OD=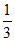 AD=
AD=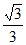 。 ……… 10分
。 ……… 10分
在Rt△POD中,PO=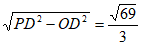 ,……… 11分
,……… 11分
所以正三棱锥P-
ABC的体积为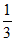 S△ABC ·PO=
S△ABC ·PO=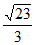 。
。
……… 13分
19.(共12分)
解:(Ⅰ)因为C=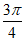 ,所以A
,所以A
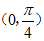 。 ……… 1分
。 ……… 1分
所以cos A=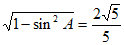 。……… 3 分
。……… 3 分
由已知得B=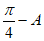 ,
,
……… 4 分
所以sinB=sin(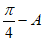 )=sin
)=sin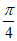 cosA- cos
cosA- cos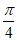 sinA=
sinA=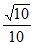 。……… 6 分
。……… 6 分
(Ⅱ)由正弦定理得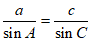 , ……… 8 分
, ……… 8 分
所以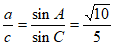 。……… 9 分
。……… 9 分
又因为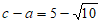 ,
,
解得a=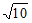 ,c=5。……… 10分
,c=5。……… 10分
所以S△ABC=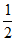 ac sinB=
ac sinB=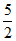
12 分
20.(共14分)
解:(Ⅰ)由sin x+ cos x≠0, …… 1分
得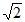 sin(x+
sin(x+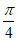 )≠0,……… 2 分
)≠0,……… 2 分
所以x+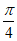 ≠kπ,其中k
≠kπ,其中k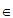 Z。 ……… 3分
Z。 ……… 3分
所以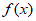 的定义域为{x |
的定义域为{x |
x≠kπ-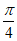 ,k
,k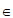 Z}。………4分
Z}。………4分
(Ⅱ)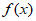 =
=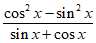 ……… 6分
……… 6分
=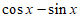 ……… 7分
……… 7分
=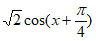 。 ……… 8分
。 ……… 8分
因为0≤x≤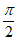 ,
,
所以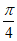 ≤x+
≤x+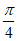 ≤
≤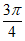 ,……… 9分
,……… 9分
所以当x+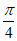 =
=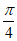 ,即x=0时,
,即x=0时,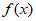 取得最大值1。……… 11分
取得最大值1。……… 11分
(Ⅲ)因为函数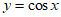 的单调递减区间为[2k π,2kπ+π] (k
的单调递减区间为[2k π,2kπ+π] (k Z)。……… 12分
Z)。……… 12分
由2k π ≤ x+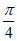 ≤ 2k π+π,x≠kπ-
≤ 2k π+π,x≠kπ-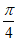 (k
(k Z),……… 13分
Z),……… 13分
得2kπ-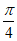 <x<2k π+
<x<2k π+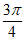 (k
(k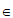 Z)。
Z)。
所以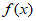 的单调递减区间为(2kπ-
的单调递减区间为(2kπ-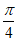 ,2kπ+
,2kπ+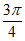 (k
(k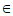 Z)。……… 14分
Z)。……… 14分
21.(共12分)
解:(Ⅰ)在正方形DCC1D1中,直线D1E与直线DC相交,
设D1E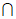 DC=F,连结AF。……… 2分
DC=F,连结AF。……… 2分
因为F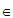 DC
DC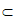 平面ABCD,
平面ABCD,
且F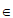 D1E
D1E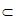 平面AD1E。 ……… 4分
平面AD1E。 ……… 4分
所以平面AD1E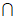 底面ABCD=AF。… 5分
底面ABCD=AF。… 5分
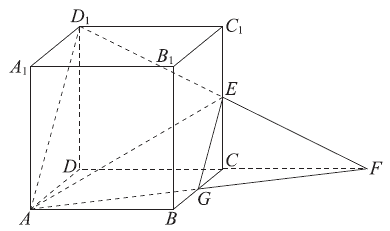
(Ⅱ)设BC AF=G,连结GE。
AF=G,连结GE。
由E为CC1的中点,得G为BC的中点,
所以EG // AD1 。……… 7分
所以平面AD1E将正方体分成两部分,其中一部分是三棱台CGE-
DAD1。
……… 8分
设正方体ABCD-A1B1C1D1的棱长为2。
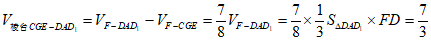 。…… 10分
。…… 10分
所以另一部分几何体的体积为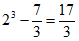 ,……… 11分
,……… 11分
所以两部分的体积之比是7:17。……… 12分
22.(共13分)
解:(Ⅰ)当OA⊥OP时,在△POB中,由余弦定理,得
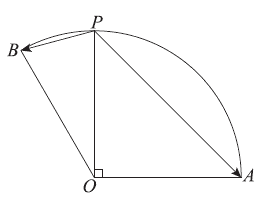
PB2=OB2+OP2-2OB·OP cos∠POB
=22+22-2×2×2×cos 30°
=8-4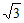 , ……… 2分
, ……… 2分
所以|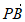 |=
|=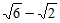 。……… 3 分
。……… 3 分
又因为|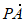 |=2
|=2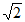 ,∠APB=120°,
,∠APB=120°,
所以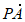 ·
·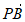 =|
=|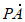 ||
||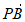 | cos∠APB=2-2
| cos∠APB=2-2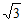 。……… 5 分
。……… 5 分
(Ⅱ)以O为原点,OA所在直线为x轴,建立如图所示的直角坐标系。 ……… 6分
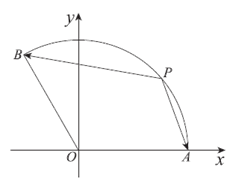
由题意知A(2,0),由∠AOB=120°,得B(-1,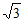 )。
)。
设P(2cos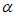 ,2sin
,2sin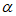 ),其中
),其中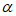
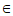 [0,
[0, ]。……… 7分
]。……… 7分
则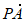 ·
·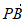 =(2-2cos
=(2-2cos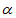 ,-2sin
,-2sin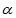 )·(-1-2 cos
)·(-1-2 cos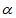 ,
,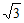 -2sin
-2sin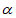 ) ……… 8分
) ……… 8分
=-2-2cos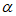 +4 cos2
+4 cos2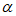 -2
-2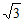 sin
sin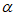 +4sin2
+4sin2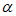
=-2 cos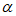 -2
-2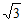 sin
sin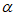 +2
+2
=-4sin(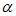 +
+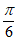 )+2。……… 10分
)+2。……… 10分
因为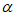
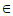 [0,
[0,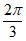 ],
],
所以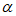 +
+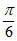
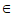 [
[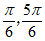 ],
],
所以sin(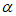 +
+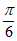 )
)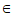 [
[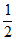 ,1],……… 11分
,1],……… 11分
所以当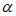 =
=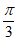 时,
时,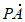 ·
·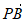 取得最小值-2。……… 13分
取得最小值-2。……… 13分
