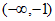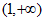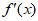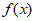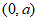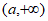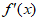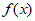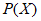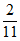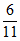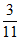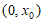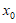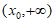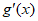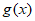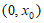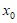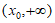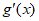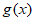本试卷共150分,考试时长120分钟。
第一部分(选择题 共40分)
一、选择题:共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 在复平面内,复数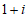 的共轭复数所对应的点位于
的共轭复数所对应的点位于
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 函数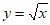 在
在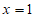 处的瞬时变化率为
处的瞬时变化率为
A. 2 B.  C.
C. 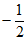 D. 1
D. 1
3. 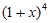 的展开式中
的展开式中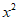 的系数是
的系数是
A. 8 B. 7 C. 6 D. 4
4. 曲线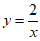 在点
在点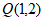 处的切线方程为
处的切线方程为
A. 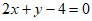 B.
B.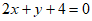
C. 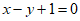 D.
D.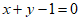
5. 某批数量很大的产品的次品率为p,从中任意取出4件,则其中恰好含有3件次品的概率是
A. 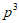 B.
B. 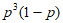 C.
C. 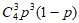 D.
D.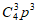
6. 已知某一离散型随机变量X的分布列如下,且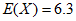 ,则a的值为
,则a的值为
X | 4 | a | 9 |
P | 0.5 | 0.1 | b |
A. 5 B. 6 C. 7 D. 8
7. 已知函数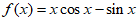 ,则
,则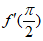 的值为
的值为
A. 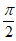 B.
B. 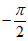 C. -1 D.
C. -1 D.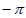
8. 已知函数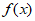 和
和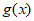 的导函数
的导函数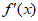 、
、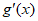 图象分别如图所示,则关于函数
图象分别如图所示,则关于函数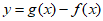 的判断正确的是
的判断正确的是
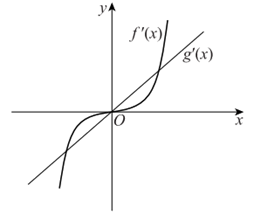
A. 有3个极大值点
B. 有3个极小值点
C. 有1个极大值点和2个极小值点
D. 有2个极大值点和1个极小值点
9. 万历十二年,中国明代音乐理论家和数学家朱载堉在其著作《律学新说》中,首次用珠算开方的办法计算出了十二个半音音阶的半音比例,这十二个半音音阶称为十二平均律,十二平均律包括六个阳律(黄钟、太族、姑洗、蕤宾、夷则、无射)和六个阴律(大吕、夹钟、仲吕、林钟、南吕、应钟)。现从这十二平均律中取出2个阳律和2个阴律,排成一个序列,组成一种旋律,要求序列中的两个阳律相邻,两个阴律不相邻,则可组成不同的旋律
A. 450种 B. 900种 C. 1350种 D. 1800种
10. 设函数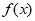 定义域为D,若函数
定义域为D,若函数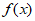 满足:对任意
满足:对任意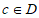 ,存在
,存在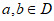 ,使得
,使得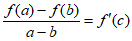 成立,则称函数
成立,则称函数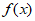 满足性质
满足性质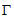 ,下列函数不满足性质
,下列函数不满足性质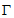 的是
的是
A. 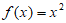 B.
B. 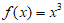 C.
C. 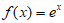 D.
D.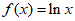
第二部分(非选择题 共110分)
二、填空题:共6小题,每小题5分,共30分。
11. 若复数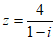 ,则
,则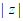 =____________。
=____________。
12. 在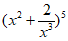 的展开式中,常数项为____________。(用数字作答)
的展开式中,常数项为____________。(用数字作答)
13. 从3名男医生和5名女医生中,选派3人组成医疗小分队,要求男、女医生都有,则不同的选取方法种数为________________。(用数字作答)
14. 中国福利彩票3D游戏(以下简称3D),是以一个3位自然数(如:0记作000)为投注号码的彩票,投注者从000~999这些3位自然数中选择一个进行投注,每注2元,如果与官方公布的三位数相同,则视为中奖,获得奖金1000元,反之则获得奖金0元,某人随机投了一注,他的奖金的期望是_____________元。
15. 能说明”若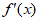 为偶函数,则
为偶函数,则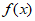 为奇函数”为假命题的一个函数是__________。
为奇函数”为假命题的一个函数是__________。
16. 辛普森悖论(Simpson’s Paradox)有人译为辛普森诡论,在统计学中亦有人称为”逆论”,甚至有人视之为”魔术”,辛普森悖论为英国统计学家E. H. 辛普森(E. H. Simpson)于1951年提出的,辛普森悖论的内容大意是”在某个条件下的两组数据,分别讨论时都会满足某种性质,可是一旦合并考虑,却可能导致相反的结论。”
下面这个案例可以让我们感受到这个悖论:关于某高校法学院和商学院新学期已完成的招生情况,现有如下数据
某高校 | 申请人数 | 性别 | 录取率 |
法学院 | 200人 | 男 | 50% |
女 | 70% | ||
商学院 | 300人 | 男 | 60% |
女 | 90% |
对于此次招生 给出下列四个结论:
①法学院的录取率小于商学院的录取率;
②这两个学院所有男生的录取率小于这两个学院所有女生的录取率;
③这两个学院所有男生的录取率不一定小于这两个学院所有女生的录取率;
④法学院的录取率不一定小于这两个学院所有学生的录取率。
其中,所有正确结论的序号是______________。
三、解答题:共6小题,共80分。解答应写出文字说明,演算步骤或证明过程。
17. (本小题满分13分)
已知函数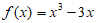 。
。
(Ⅰ)求函数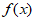 的单调区间;
的单调区间;
(Ⅱ)求函数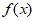 在区间
在区间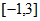 上的最大值和最小值。
上的最大值和最小值。
18.(本小题满分13分)
某射手打靶命中8环、9环、10环的概率分别为0.15、0.25、0.2,如果他连续打靶三次,且每次打靶的命中结果互不影响。
(Ⅰ)求该射手命中29环的概率;
(Ⅱ)求该射手命中不少于28环的概率。
19. (本小题满分13分)
已知函数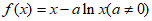 。
。
(Ⅰ)当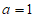 时,求曲线
时,求曲线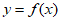 在点
在点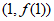 处的切线方程;
处的切线方程;
(Ⅱ)求函数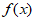 的极值点和极值。
的极值点和极值。
20. (本小题满分14分)
高中必修课程结束之后,学生需要从物理、化学、生物、历史、地理、政治六科中选择三科,继续学习选择性必修课程,某地记者为了了解本地区高一学生的选择意向,随机采访了100名学生作为样本进行情况调研,得到下表:
组别 | 选考科目 | 频数 |
第1组 | 历史、地理、政治 | 20 |
第2组 | 物理、化学、生物 | 17 |
第3组 | 生物、历史、地理 | 14 |
第4组 | 化学、生物、地理 | 12 |
第5组 | 物理、化学、地理 | 10 |
第6组 | 物理、生物、地理 | 9 |
第7组 | 化学、历史、地理 | 7 |
第8组 | 物理、历史、地理 | 5 |
第8组 | 化学、生物、政治 | 4 |
第10组 | 生物、地理、政治 | 2 |
合计:100 |
(Ⅰ)从样本中随机选1名学生,求该学生选择了化学的概率;
(Ⅱ)从第8组、第9组、第10组中,随机选2名学生,记其中选择政治的人数为X,求X的分布列和期望;
(Ⅲ)如果这个地区一名高一学生选择了地理,则在其它五科中,他同时选择哪一科的可能性最大?并说明理由。
21. (本小题满分13分)
已知函数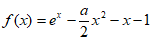 。
。
(Ⅰ)若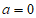 ,证明:
,证明: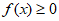 ;
;
(Ⅱ)若曲线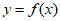 的切线斜率不存在最小值,求a的取值范围。
的切线斜率不存在最小值,求a的取值范围。
22. (本小题满分14分)
已知函数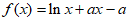 。
。
(Ⅰ)求函数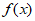 的单调区间;
的单调区间;
(Ⅱ)求证:当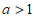 时,函数
时,函数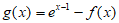 存在最小值,且最小值小于1。
存在最小值,且最小值小于1。
【试题答案】
一、选择题:共10小题,每小题4分,共40分。
1. D 2. B 3. C 4. A 5. C 6. C 7. B 8. D 9. B 10. B
二、填空题:共6小题,每小题5分,共30分。
11. 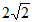 12. 40 13. 45 14. 1 15.
12. 40 13. 45 14. 1 15. 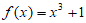 (答案不唯一) 16. ②④
(答案不唯一) 16. ②④
注:第16小题只选对一个正确命题得2分,错选不得分。
三、解答题:共6小题,共80分。解答应写出文字说明,演算步骤或证明过程。
17.(本小题满分13分)
解:(Ⅰ)因为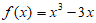 ,所以
,所以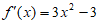 。 3分
。 3分
令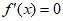 ,解得
,解得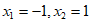 。
。
随着x的变化,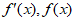 变化情况如下表:
变化情况如下表:
x |
| -1 | (-1,1) | 1 |
|
| + | 0 | - | 0 | + |
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
8分
所以,函数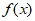 的单调递增区间为
的单调递增区间为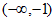 和
和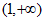 ,单调递减区间为
,单调递减区间为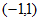 。
。
9分
(Ⅱ)因为函数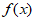 在区间
在区间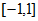 上单调递减,在区间
上单调递减,在区间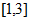 上单调递增,
上单调递增,
又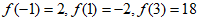 , 11分
, 11分
所以,函数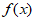 在区间
在区间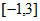 上的最大值为18,最小值为-2。 13分
上的最大值为18,最小值为-2。 13分
18. (本小题满分13分)
解:(Ⅰ)设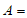 “连续射击3次,中29环”,
“连续射击3次,中29环”,
则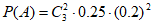 4分
4分
=0.03
所以该射手命中29环的概率为0.03。 5分
(Ⅱ)设B=”连续射击3次,命中不少于28环”,
依题意,命中30环的概率为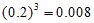 ; 7分
; 7分
命中28环的概率为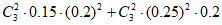 11分
11分
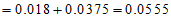 ; 12分
; 12分
由(1)知,命中29环的概率为0.03;
所以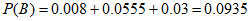 , 13分
, 13分
所以该射手连续射击3次,命中不少于28环的概率为0.0935。
19. (本小题满分13分)
解:(Ⅰ)当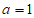 时,
时,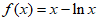 ,所以
,所以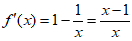 , 3分
, 3分
所以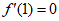 ,
,
又因为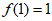 ,所以曲线
,所以曲线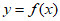 在点
在点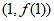 处的切线方程为
处的切线方程为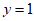 。 5分
。 5分
(Ⅱ)由已知,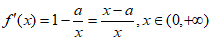 ,
,
①当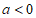 时,
时,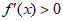 ,
,
函数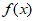 在定义域内是增函数,不存在极值。 7分
在定义域内是增函数,不存在极值。 7分
②当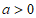 时,令
时,令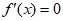 ,解得
,解得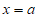 ,
,
随着x的变化,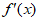 ,
,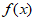 变化情况如下表:
变化情况如下表:
x |
| a |
|
| - | 0 | + |
| ↘ | 极小值 | ↗ |
9分
所以,函数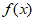 在区间
在区间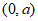 上单调递减,在区间
上单调递减,在区间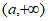 上单调递增, 10分
上单调递增, 10分
所以,函数 的极小值点为
的极小值点为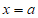 ,极小值为
,极小值为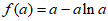 , 12分
, 12分
函数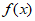 不存在极大值。 13分
不存在极大值。 13分
综上,当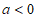 时,函数
时,函数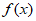 没有极值;当
没有极值;当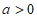 时,
时,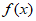 有极小值
有极小值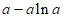 ,极小值点为
,极小值点为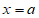 ,无极大值。
,无极大值。
20. (本小题满分14分)
解:(Ⅰ)设A=”从样本中随机选1人,该学生选择了化学”,
则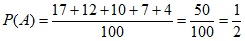 ,
,
所以,从样本中随机选1人,该学生选择了化学的概率为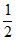 。 4分
。 4分
(Ⅱ)第8、9、10组共有11人,其中选择政治的有6人。
所以X的所有可能取值为0,1,2。 5分
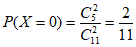 , 6分
, 6分
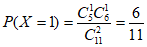 , 7分
, 7分
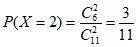 。 8分
。 8分
所以X的分布列为
X | 0 | 1 | 2 |
|
|
|
|
9分
故X的期望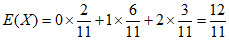 。 11分
。 11分
(Ⅲ)选择地理的总人数为: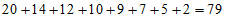 。
。
所以P(”同时选择生物”)=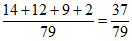 ;
;
P(”同时选择化学”)=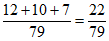 ;
;
P(”同时选择政治”)=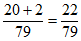 ;
;
P(”同时选择物理”)=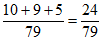 ;
;
P(”同时选择历史”)=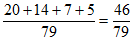 。 13分
。 13分
因为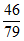 最大,所以一个学生选择了地理,同时选择历史的可能性最大。 14分
最大,所以一个学生选择了地理,同时选择历史的可能性最大。 14分
21.(本小题满分13分)
解:(Ⅰ)当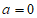 时,
时,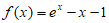 ,所以
,所以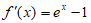 , 1分
, 1分
解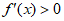 ,得
,得 ;解
;解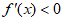 ,得
,得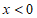 ,
,
所以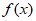 在区间
在区间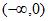 上单调递减,在区间
上单调递减,在区间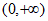 上单调递增, 3分
上单调递增, 3分
所以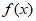 的最小值为
的最小值为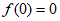 ,
,
所以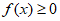 。 5分
。 5分
(Ⅱ)因为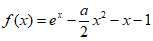 ,所以
,所以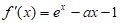 ,
,
设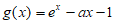 ,
,
则曲线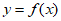 的切线斜率不存在最小值等价于
的切线斜率不存在最小值等价于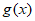 不存在最小值。 7分
不存在最小值。 7分
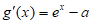 。
。
①当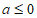 时,
时,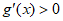 恒成立,
恒成立,
所以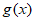 在区间
在区间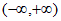 上单调递增,不存在最小值,
上单调递增,不存在最小值,
所以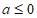 符合题意。 9分
符合题意。 9分
②当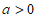 时,
时,
解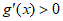 ,得
,得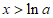 ;解
;解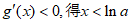 ,
,
所以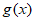 在区间
在区间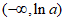 上单调递减,在区间
上单调递减,在区间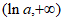 上单调递增, 10分
上单调递增, 10分
所以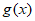 在
在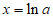 处取得最小值,
处取得最小值,
所以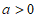 不符合题意。 12分
不符合题意。 12分
综上,a的取值范围为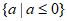 。 13分
。 13分
22. (本小题满分14分)
解:(Ⅰ)函数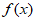 定义域为
定义域为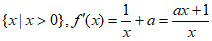 。
。
①当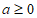 时,
时,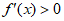 恒成立,函数
恒成立,函数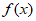 的单调递增区间为
的单调递增区间为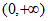 。 2分
。 2分
②当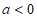 时,
时,
解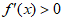 ,得
,得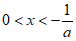 ;解
;解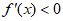 ,得
,得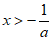 ,
,
所以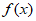 的单调递增区间为
的单调递增区间为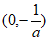 ,单调递减区间为
,单调递减区间为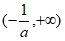 。 4分
。 4分
综上,当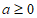 时,
时,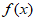 单调递增区间为
单调递增区间为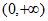 ;当
;当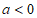 时,
时,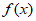 的单调递增区间为
的单调递增区间为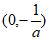 ,单调递减区间为
,单调递减区间为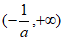 。
。
(Ⅱ)证法1:由已知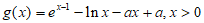 。
。
因为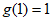 ,
,
所以只需证明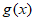 存在最小值,但
存在最小值,但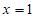 不是最小值点,即
不是最小值点,即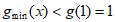 。6分
。6分
因为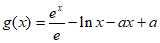 ,所以
,所以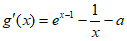 ,
,
因为函数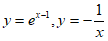 在区间
在区间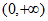 上是增函数,
上是增函数,
所以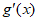 在区间
在区间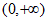 上是增函数, 8分
上是增函数, 8分
因为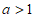 ,所以
,所以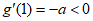 ,
,
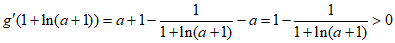 ,
,
所以方程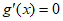 在区间
在区间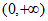 上存在唯一解, 10分
上存在唯一解, 10分
不妨设为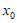 ,则
,则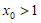 ,
,
随着x的变化,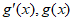 变化情况如下表:
变化情况如下表:
x |
|
|
|
| - | 0 | + |
| ↘ | 极小值 | ↗ |
所以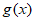 有最小值,最小值为
有最小值,最小值为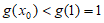 , 13分
, 13分
所以函数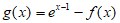 存在最小值,且最小值小于1。 14分
存在最小值,且最小值小于1。 14分
证法2:由已知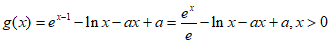 ,
,
所以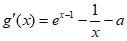 ,
,
因为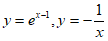 在区间
在区间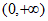 上是增函数,
上是增函数,
所以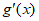 在
在 上是增函数, 6分
上是增函数, 6分
因为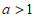 ,所以
,所以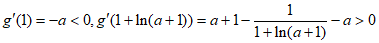 ,
,
所以方程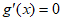 存在唯一解, 8分
存在唯一解, 8分
不妨设为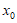 ,则
,则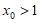 ,
,
随着x的变化,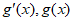 变化情况如下表:
变化情况如下表:
x |
|
|
|
| - | 0 | + |
| ↘ | 极小值 | ↗ |
所以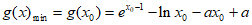 ,且
,且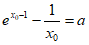 , 10分
, 10分
所以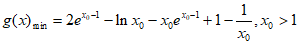 。
。
设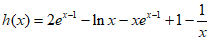 ,
,
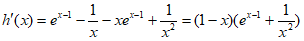 ,
,
当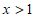 时,
时,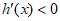 ,所以
,所以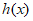 在区间
在区间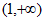 上单调递减, 12分
上单调递减, 12分
所以当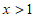 时,
时,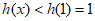 ,即
,即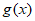 的最小值小于1, 13分
的最小值小于1, 13分
所以函数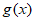 存在最小值,且最小值小于1。 14分
存在最小值,且最小值小于1。 14分