本试卷共三道大题,26道小题。满分100分。考试时间100分钟。
一、选择题(本题共30分,每小题3分)
第1—10题均有四个选项,符合题意的选项只有一个。
1. -8的立方根是
A. -4 B. -2 C. 2 D. ±2
2. 将不等式的解集x>6表示在数轴上,下列图形中正确的是

A B C D
3. 点P(-5,4)所在的象限是
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4. 下列各数中的无理数是
A. 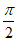 B.
B. 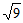 C.
C. 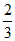 D. -6
D. -6
5. 已知m >n,下列结论中正确的是
A. m +2<n+2 B. m -2<n-2
C. -2m >-2n D. 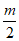 >
>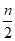
6. 下列各图中,线段CD是△ABC的高的是
A. 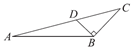 B.
B.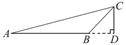
C.  D.
D.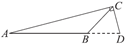
7. 如图,分别将木条a,b 与木条c 钉在一起,若∠1=50°,∠2=80°,要使木条a 与b 平行,则木条a需要顺时针转动的最小度数为
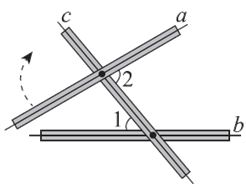
A. 30° B. 50° C. 80° D. 130°
8. 下列命题中正确的是
A. 如果两个角相等,那么这两个角一定是对顶角
B. 如果两个角互为补角,那么这两个角一定是邻补角
C. 如果两条直线都与第三条直线平行,那么这两条直线也互相平行
D. 如果两条平行线被第三条直线所截,那么同旁内角相等
9. 党的十八大以来,我国实施精准扶贫精准脱贫,全面打响了脱贫攻坚战,扶贫工作取得了决定性进展。下面的统计图反映了我国五年来农村贫困人口的相关情况,其中“贫困发生率“是指贫困人口占目标调查人口的百分比。
2015~2019年年末全国农村贫困人口和贫困发生率统计图
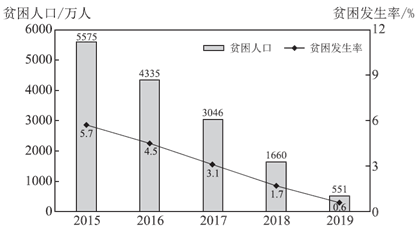
根据统计图提供的信息,下列推断中不合理的是
A. 与2018年相比,2019年年末全国农村贫困人口减少了1109万人
B. 2015~2019年年末,与上一年相比,全国农村贫困人口的减少量均超过1000万
C. 2015~2019年年末,与上一年相比,全国农村贫困发生率逐年下降
D. 2015~2019年年末,与上一年相比,全国农村贫困发生率下降均不少于1. 2%
10. 已知关于x 的不等式2x-m <1-x 的正整数解是1,2,3,则m 的取值范围是
A. 3<m ≤4 B. 3≤m <4 C. 8<m ≤11 D. 8≤m <11
二、填空题(本题共18分,第13,18题每小题3分,其余每小题2分)
11. 计算:|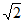 –
–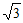 |=_________。
|=_________。
12. 小芸为了解同学们最感兴趣的在线学习方式,设计了如下的调查问题(选项不完整):
你最感兴趣的一种在线学习方式是(
|
她准备从“①在线听课,②在线讨论,③在线学习2~3小时,④用手机在线学习,⑤在线阅读“中选取三个作为该问题的备选答案,合理的选取是_________。(填序号)
13. 将一把直尺与一块含30°角的三角板按如图方式摆放。
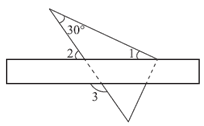
若∠1=25°,则∠2=_________°,∠3=_________°。
14. 已知点A(m -1,2m +3)在 y轴上,则点A的坐标为_________。
15. 若一个多边形的每个内角都是140°,则这个多边形的边数为_________。
16. 用一组a,b,c的值说明命题 “若a>b,则ac>bc。“是假命题,这组值可以是a=_________,b=_________,c=_________。
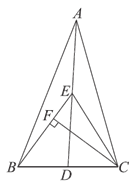
17. 如图,AD 是△ABC的中线,E是AD的中点,连接EB,EC,CF⊥BE于点F。若BE=9,CF=8,则△ACE的面积为________。
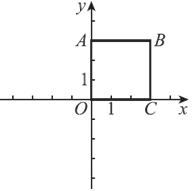
18. 如图,在平面直角坐标系xOy中,点A,B,C的坐标分别为(0,3),(3,3),(3,0)。正方形OABC 从图中的位置出发,以每秒旋转90°的速度,绕点O 沿顺时针方向旋转。同时,点P从点O 出发,以每秒移动1个单位长度的速度,沿正方形的边,按照O→A→B→C→O →A…的路线循环运动。第1秒时点P的坐标为(1,0),第2秒时点P的坐标为________,第2020秒时点P 的坐标为________。
三、解答题(本题共52分,第19~22题每小题6分,第23~26题每小题7分)
19. 解不等式组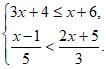
20. 小天学完平方根和开平方运算后,发现可以运用这些知识解形如x2 =a(a 为常数)的这类方程。
(1)小天先尝试解了下面两个方程:
① x2=1,解得x=1或x=-1;
② x2=-1,此方程无实数解。
方程①有两个解的依据是:正数有两个平方根,它们互为相反数;
方程②无实数解的依据是:_______________;
(2)小天进一步探究了解方程③和④:
③ 3x2=21;
④(x+2)2=9。
解:x2=7。
解:x+2=3或x+2=-3。
x= 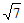 或x=-
或x=- 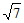 。 x=1或x=-5。
。 x=1或x=-5。
请你参考小天的方法,解下列两个方程:
⑤ 2x2-72=0;
⑥
(x-1)2=5。
21. 如图,在△ABC中,点D,E在AB边上,点F在AC边上,EF∥DC,点H在BC边上,且∠1+∠2=180°。求证:∠A=∠BDH。
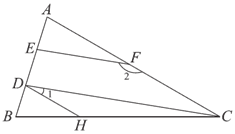
请将下面的证明过程补充完整:
证明:∵EF∥DC,
∴∠2+∠_______=180°。(理由:_______)
∵∠1+∠2=180°,
∴∠1=∠_______。
∴_______∥_______。(理由:_______)
∴∠A=∠BDH。
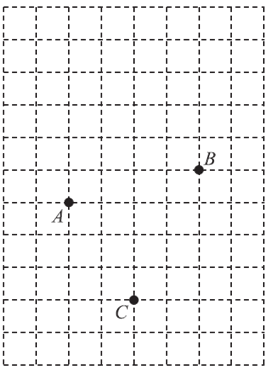
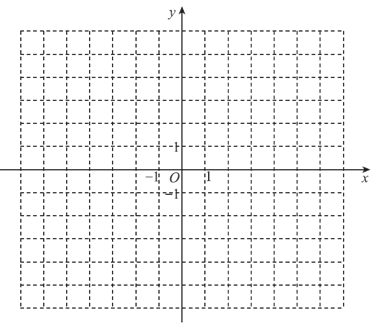
22. 在平面直角坐标系xOy 中,已知点A(0,1),B(4,2),C(2,-2)。
(1)在网格中画出这个平面直角坐标系;
(2)连接CB,平移线段CB,使点C 移动到点A,得到线段AD。
①
画出线段AD,并写出点D的坐标;
②
连接AC,DB,四边形ACBD的面积是_______。
23. 为弘扬传统文化,某校开展了“传承传统文化,阅读经典名著“活动,并举行了经典名著知识竞赛。为了解七年级学生(七年级有8个班,共320名学生)的阅读效果,综合实践调查小组开展了一次调查研究。
收集数据
(1)调查小组计划选取40名学生的竞赛成绩(百分制)作为样本,下面的抽样方法中,合理的是_________;(填字母)
A. 抽取七年级1班、2班各20名学生的竞赛成绩组成样本
B. 抽取各班竞赛成绩较好的共40名学生的竞赛成绩组成样本
C. 从年级中按学号随机选取40名学生的竞赛成绩组成样本
整理、描述数据
抽样方法确定后,调查小组收集到了40名学生的竞赛成绩,其中竞赛成绩x 在80≤x≤100范围的具体成绩如下:
90,92,81,82,95,86,88,89,86,93,97,100,80,
81,86,89,82,85,98,90,97,100,84,87,92,96。
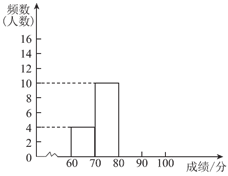
整理数据,得到如下频数分布表和频数分布直方图(不完整):
|
|
(2)请补全以上频数分布表和频数分布直方图;
应用数据
(3)若竞赛成绩不低于90分的记为 “优秀“,请你估计参加这次知识竞赛的全年级320名学生中,竞赛成绩为 “优秀“的约有多少人?
24. 某公园为了方便游客游览,设置了观光接驳车。公园设计的其中一条观光路线上设有A,B,C,D四个站点(如图所示),相邻两个站点的距离都是5千米,游客只能在站点上、下车。一辆接驳车在A,D之间往返行驶,一名游客在距离A 站点x 千米(5<x<10)的M 处徒步游览时,临时有事要赶回站点A,此时他正好遇到开往站点D 的接驳车,他决定走到站点B 等待刚才那辆车从站点D 开回。已知接驳车行驶的平均速度为30千米/时,该游客步行的平均速度为6千米/时,游客上下车的时间忽略不计。

(1)接驳车在A,D 之间往返行驶一次所需时间为_______小时;
(2)该游客从 M 处走到站点B 所需时间为_______小时;(用含x 的式子表示)
(3)如果该游客不晚于接驳车到达了站点B,那么当时他离站点A 的距离x 最多有多远?
25. 对于平面直角坐标系xOy 中的任意一点P (x,y),给出如下定义:记a=x+y,b=-y,将点M(a,b)与N(b,a)称为点P的一对“相伴点“。
例如:点P(2,3)的一对 “相伴点“是点
(5,-3)与(-3,5)。
(1)点Q(4,-1)的一对 “相伴点“的坐标是_________与_________;
(2)若点A(8,y)的一对 “相伴点“重合,则y 的值为_________;
(3)若点B 的一个 “相伴点“的坐标为(-1,7),求点B 的坐标;
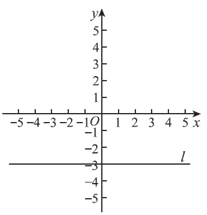
(4)如图,直线l
经过点(0,-3)且平行于x 轴。若点C 是直线l上的一个动点,点M与N是点C的一对“相伴点“,在图中画出所有符合条件的点 M,N 组成的图形。
26. 已知△ABC,过点B 作DE⊥BC 于点B,过点C 作FH ∥DE。
(1)BC 与FH 的位置关系是________;
(2)如图1,点M在直线DE和FH之间,连接BM,CM。若∠ABM=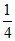 ∠ABD,∠ACM =
∠ABD,∠ACM =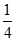 ∠ACF,∠BAC=72°,求∠BMC的度数;
∠ACF,∠BAC=72°,求∠BMC的度数;
(3)若∠ABE 和∠ACH 的平分线交于点N,在图2中补全图形,用等式表示∠BNC与∠BAC 的数量关系,并证明。
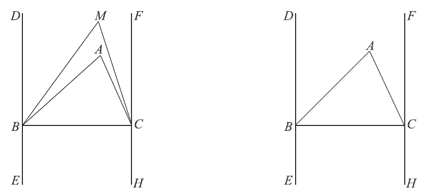
图1 图2
附加题
试卷满分:20分
一、解答题(本题共13分,第1题6分,第2题7分)
1. 已知一个三角形的三条边的长分别为n+2,n+6,3n。
(1)n+2_______n+6;(填 “>”,“=”或 “<“)
(2)若这个三角形是等腰三角形,求它的三边的长;
(3)若这个三角形的三条边都不相等,且n为正整数,直接写出n 的最大值。
2. 在△ABC中,BD是△ABC的角平分线,点E在射线DC上,EF⊥BC于点F,EM平分∠AEF交直线AB于点M。
(1)如图1,点E在线段DC上,若∠A=90°,∠M =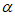 。
。
①
∠AEF=________;(用含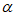 的式子表示)
的式子表示)
②
求证:BD ∥ME;
(2)如图2,点E 在DC 的延长线上,EM 交BD 的延长线于点N,用等式表示∠BNE与∠BAC的数量关系,并证明。
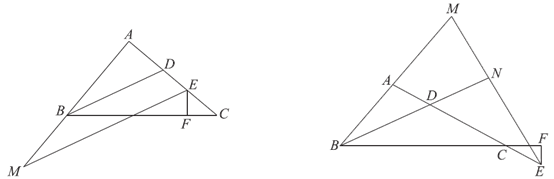
图1 图2
二、阅读探究题(本题7分)
3. 在平面直角坐标系xOy中,横、纵坐标都是整数的点叫做整点。给出如下定义:对于任意两个整点M (x1,y1),N(x2,y2),M与N的“直角距离“记为dMN,dMN =|x1-x2|+|y1-y2|。
例如,点M(1,5)与N(7,2)的“直角距离“dMN=|1-7|+|5-2|=9。
(1)已知点A(4,-1)。
①
点A 与点B(1,3)的 “直角距离“dAB = ________;
②
若点A 与整点C(-2,m)的 “直角距离“dAC =8,则m的值为________;
(2)小明有一项设计某社区规划图的实践作业,这个社区的道路都是正南正北,正东正西方向,并且平行的相邻两条路之间的距离都是相等的,可近似看作正方形的网格。小明建立平面直角坐标系画出了此社区的示意图(如图所示)。
为了做好社区消防,需要在某个整点处建一个消防站P,要求是:消防站与各个火警高危点的“直角距离“之和最小。目前该社区内有两个火警高危点,分别是D(-2,-1)和E(2,2)。
①
若对于火警高危点D 和E,消防站P 不仅要满足上述条件,还需要消防站P 到D,E两个点的 “直角距离“之差的绝对值最小,则满足条件的消防站P 的坐标可以是 _______(写出一个即可),所有满足条件的消防站P 的位置共有_______个;
②
在设计过程中,如果社区还有一个火警高危点F(4,-2),那么满足与这三个火警高危点的“直角距离“之和最小的消防站P 的坐标为_______。
参考答案
一、选择题(本题共30分,每小题3分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | B | C | B | A | D | B | A | C | D | C |
二、填空题(本题共18分,第13,18 题每小题3分,其余每小题2分)
11.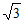 –
–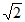 。 12.①②⑤。 13.55,125。
。 12.①②⑤。 13.55,125。
14.(0,5)。 15.9。
16.答案不唯一,如:a= 2,b=1,c=-1。
17.18。
18.(0,-2),(1,3)。
(说明:第16题列举对
a>b 得1分,全对得2分;第13,18 题答对一个空得2分,全对得3分)
三、解答题(本题共52分,第19~22题每小题6分,第23~26题每小题7分)
19.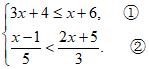
解:解不等式①,得x≤1。 2分
解不等式②,得x>-4。 5分
所以原不等式组的解集为-4<x≤1。 6分
20.(1)负数没有平方根; 2分
(2)⑤2x2-72=0
解:x2=36。
x= 6或x=-6。 4分
⑥(x-1)2=5
解:x-1=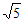 或x-1=-
或x-1=-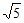 。
。
x=1+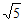 或x=1-
或x=1-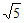 。 6分
。 6分
21. 证明:∵EF∥DC,
∴∠2+∠FCD__ =180°。 1 分
(理由:两直线平行,同旁内角互补__) 2 分
∵∠1+∠2=180°,
∴∠1=∠__FCD__。
3 分
∴__DH∥AC。 5分
(理由:内错角相等,两直线平行) 6 分
∴∠A=∠BDH。
22. 解:(1)坐标系如图所示; 2 分
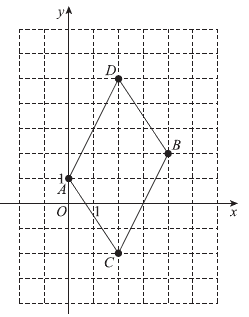
(2)①线段
AD 如图所示, 3 分
点
D 的坐标为(2,5); 5 分
② 14。 6 分
23.解:(1)C; 2 分
(2)补全频数分布表和频数分布直方图如下:
成绩 | 频数 | |
60≤x<70 | 4 | |
70≤x<80 | 10 | 3分 |
80≤x<90 | 14 | 4分 |
90≤x≤100 | 12 | 5分 |
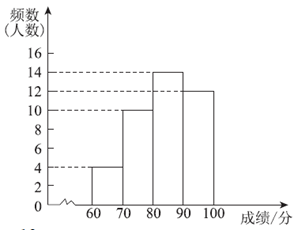 ……………6 分
……………6 分
(3)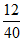 ×320= 96(人)。 7 分
×320= 96(人)。 7 分
答:估计全体七年级学生中,竞赛成绩为“优秀“的约有96人。
24.解:(1)1; 2 分
(2)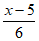 ; 3 分
; 3 分
(3)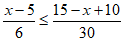 。 5 分
。 5 分
解得x≤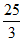 。 6 分
。 6 分
答:该游客离站点A的距离最远为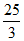 千米. 7 分
千米. 7 分
25.解:(1)(3,1),(1,3); 2 分
(2)-4; 3 分
(3)设点B 的坐标为(x,y),
则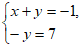 或
或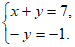
解得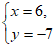 或
或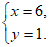
∴点
B 的坐标为(6,-7)或(6,1); 5 分
(4)如图所示。
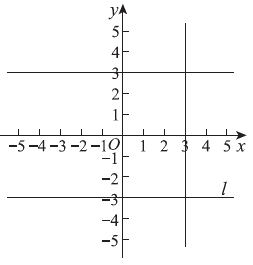 …………………7 分
…………………7 分
26.解:(1)BC⊥FH; 2 分
(2)如图1。
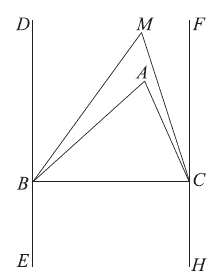
图 1
∵FH∥DE,
∴∠DBC+∠FCB=180°。
∴∠ABD+∠ACF=180°-∠ABC-∠ACB。
∵在△ABC 中,∠BAC =180°-∠ABC-∠ACB,
∴∠ABD+∠ACF=∠BAC =72°。
∵∠ABM=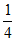 ∠ABD,∠ACM=
∠ABD,∠ACM=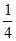 ∠ACF,
∠ACF,
∴∠ABM+∠ACM=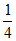 ∠ABD+
∠ABD+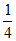 ∠ACF
∠ACF
=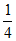 (∠ABD+∠ACF)=18°。
(∠ABD+∠ACF)=18°。
∴在△MBC 中,∠BMC =180°-∠MBC-∠MCB
=180°-(∠ABM+∠ACM)-(∠ABC+∠ACB)
=180°-18°-(180°-72°)
=54°。 4 分
(3)∠BAC+2∠BNC=360°。 5 分
证明:过点N 作直线 PQ∥DE,如图2。
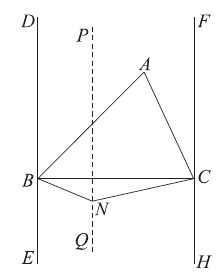
图2
∵PQ∥DE,
∴∠PNB=∠EBN。
∵FH∥DE,PQ∥DE,
∴FH∥PQ。
∴∠PNC=∠HCN。
∴∠BNC=∠PNB+∠PNC
=∠EBN+∠HCN。
∵BN,CN 分别平分∠ABE 和∠ACH,
∴∠ABN=∠EBN,∠ACN=∠HCN。
∵在四边形 ABNC 中,
∠BAC+∠ABN+∠BNC+∠ACN =360°,
∴∠BAC+∠EBN+∠BNC+∠HCN =360°。
∴∠BAC+∠BNC+∠BNC =360°。
∴∠BAC+2∠BNC=360°. 7 分
附加题答案
一、解答题(本题共13分,第1题6分,第2题7分)
1.解:(1) <; 2 分
(2)∵这个三角形是等腰三角形,
∴ n+2=3n 或 n+ 6=3n 。
∴ n=1或 n= 3 。 4 分
当
n=1 时,三条边的长分别为3,7,3,不能构成三角形;
当
n= 3 时,三条边的长分别为5,9,9,能构成三角形。
所以三角形的三条边的长分别为5,9,9. 5 分
(3)7. 6 分
2.解:(1)① 180°-2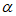 ; 2 分
; 2 分
②
证明:如图 1。
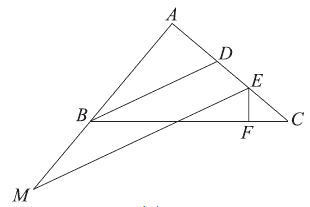
图 1
∵EF⊥BC 于点 F,
∴∠EFC=90°。
∴∠C+∠CEF =90°。
∵∠A=90°,
∴∠C+∠ABC =90°。
∴∠CEF=∠ABC。
∵∠AEF=180°-2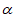 ,
,
∴∠CEF=2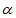 。
。
∴∠ABC=2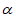 。
。
∵BD 平分∠ABC,
∴∠ABD=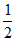 ∠ABC=
∠ABC=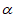 。
。
∴∠ABD=∠M。
∴BD∥ME。
4 分
(2)2∠BNE=90°+∠BAC。 5 分
证明:如图 2。
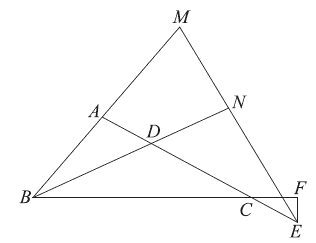
图 2
∵BD 平分∠ABC,EM 平分∠AEF,
设∠ABD=x,∠AEM=y,
∴∠ABC=2x,∠AEF=2y。
∵∠ABD+∠BAD=180°-∠ADB,
∠NED+∠END=180°-∠NDE,
而∠ADB=∠NDE,
∴∠ABD+∠BAD=∠NED+∠END。
∴x+∠BAD=y+∠END,
即 x–y=∠END-∠BAD。
同理,∠ABC+∠BAC=∠FEC+∠EFC。
∴2x+∠BAC=2y+∠EFC,
即 2x-2y=∠EFC-∠BAC。
∵EF⊥BC 于点F,
∴∠EFC=90°。
∴2(x–y)=90°-∠BAC。
∴2(∠END-∠BAD)=90°-∠BAC。
即 2(∠BNE-∠BAC)=90°-∠BAC。
∴2∠BNE=90°+∠BAC。 7 分
二、阅读探究题(本题7分)
3.解:(1)① 7; 2 分
②-3或 1; 4 分
(2)①
答案不唯一,如(0,0), 5 分
8; 6 分
②(2,-1)。 7分