本试卷共三道大题,25道小题。满分100分。考试时间100分钟。
一、选择题(本题共30分,每小题3分)
第1~10题均有四个选项,符合题意的选项只有一个。
1. 若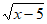 在实数范围内有意义,则x的取值范围是
在实数范围内有意义,则x的取值范围是
A. 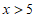 B.
B. 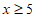 C.
C. 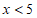 D.
D.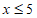
2. 下列图案中,既是轴对称图形也是中心对称图形的是
3. 下列运算正确的是
A. 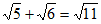 B.
B.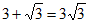
C. 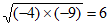 D.
D.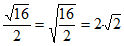
4. 如图,在Rt△ABC中,∠C=90°,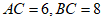 ,若D,E分别为边AC,BC的中点,则DE的长为
,若D,E分别为边AC,BC的中点,则DE的长为
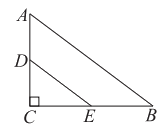
A. 10 B. 5 C. 4 D. 3
5. 下列关于一元二次方程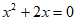 的说法正确的是
的说法正确的是
A. 该方程只有一个实数根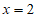 B. 该方程只有一个实数根
B. 该方程只有一个实数根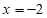
C. 该方程的实数根为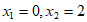 D. 该方程的实数根为
D. 该方程的实数根为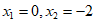
6. 下列命题正确的是
A. 一组对边平行,另一组对边相等的四边形是平行四边形
B. 对角线相等的四边形是矩形
C. 有一组邻边相等的四边形是菱形
D. 有一组邻边相等且有一个角是直角的平行四边形是正方形
7. 用配方法解一元二次方程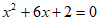 时,下列变形正确的是
时,下列变形正确的是
A. 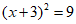 B.
B.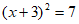
C. 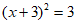 D.
D.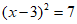
8. 甲、乙两座城市某年四季的平均气温如图所示,下列说法正确的是
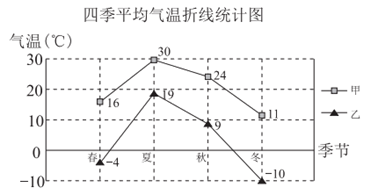
A. 甲城市的年平均气温在30℃以上
B. 乙城市的年平均气温在0℃以下
C. 甲城市的年平均气温低于乙城市的年平均气温
D. 甲、乙两座城市中,甲城市四季的平均气温较为接近
9. 图1是第七届国际数学教育大会(ICME-7)的会徽图案,它是由一串有公共顶点O的直角三角形(如图2所示)演化而成的,如果图2中的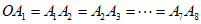 =1,那么OA8的长为
=1,那么OA8的长为
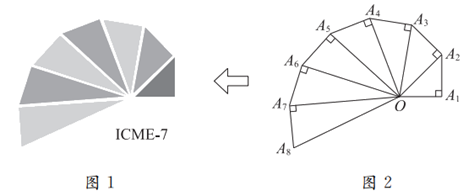
A. 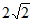 B. 3 C.
B. 3 C. 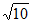 D.
D.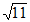
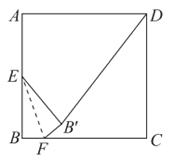
10. 如图,正方形ABCD的边长为2,E为AB边的中点,点F在BC边上,点B关于直线EF的对称点记为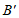 ,连接
,连接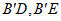 ,
,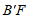 ,当点F在BC边上移动使得四边形
,当点F在BC边上移动使得四边形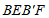 成为正方形时,
成为正方形时, 的长为
的长为
A. 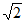 B.
B. 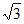 C.
C. 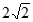 D. 3
D. 3
二、填空题(本题共26分,其中第18题5分,其余每小题3分)
11. 计算: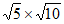 =_____________。
=_____________。
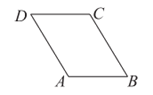
12. 如图,在平行四边形ABCD中,若∠A=2∠B,则∠D=________°。
13. 若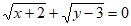 ,则
,则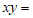 ___________。
___________。
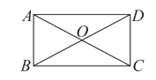
14. 如图,矩形ABCD的对角线AC与BD交于点O,若OB=5,则AC=___________。
15. 如果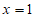 是关于x的方程
是关于x的方程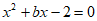 的一个根,则b=________。
的一个根,则b=________。
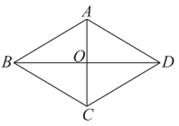
16. 如图,在菱形ABCD中,对角线AC与BD交于点O,若∠ABC=60°,OA=1,则菱形的周长等于____________。
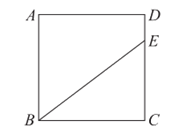
17. 如图,正方形ABCD的边长为4,点E在CD边上,CE=3,若点F在正方形的某一边上,满足CF=BE,且CF与BE的交点为M,则CM=____________。
18. 如图,在△OAB中,∠1=∠2. 将△OAB绕点O顺时针旋转180°,点A的对应点记为C,点B的对应点记为D,顺次连接BC,CD,DA得到四边形ABCD。
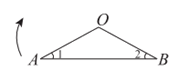
(1)补全图形;
(2)所得四边形ABCD为__________(从①矩形;②菱形;③正方形中选择,只填写序号即可),判断此结论的依据是____________。
三、解答题(本题共44分,第19~23题每小题6分,第24、25题每小题7分)
19. 计算:
(1)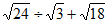 ; (2)
; (2)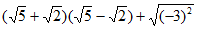 。
。
20. 解方程: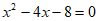 。
。
21. 如图,在平行四边形ABCD中,点E在BC边上,AE平分∠BAD,点F在AD边上,EF∥AB。
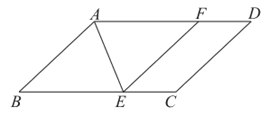
(1)求证:四边形ABEF是菱形;
(2)若AB=2,BC=3,点P在线段AE上运动,请直接回答当点P在什么位置时PC+PF取得最小值,最小值是多少。
22. 甲、乙两支运动队各有10名队员,他们的年龄分布情况分别如图1、图2所示。
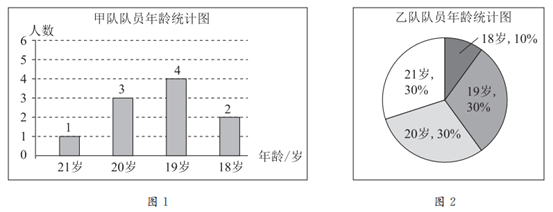
甲、乙两队队员年龄统计表
平均数(近似值) | 众数 | 中位数 | |
甲队 | a | ①_______ | ②________ |
乙队 | 20 | ③________ | b |
解决下列问题:
(1)求甲队队员的平均年龄a的值(结果取整数);
(2)补全统计表中的①②③三处;
(3)阅读理解——扇形图中求中位数的方法:
【阅读与思考】
小明同学在求乙队队员年龄的中位数b时,是这样思考的:
因为中位数是将一组数据按大小排序后,排在中间位置的一个数或中间两个数的平均数,那就需要先找到数据按大小排序后,大致排在50%附近的数,再根据中位数的概念进行细化求解。
图2这个扇形图中的数据18~21是按大小顺序旋转排列的,我们就可以像图3所示的这样,先找到最大数据”21″与最小数据”18″的分界半径OM,为找到排在50%附近的数,再作出直径MN,那么射线ON指向的数据就是中位数。
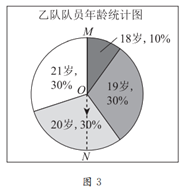
王老师的评价:小明的这个方法是从中位数的概念出发,充分利用了扇形图的特性形象直观地解决问题。
【理解与应用】
请你利用小明的方法直接写出统计表中b的值。
23. 阅读材料:
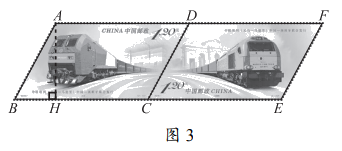
中国—西班牙联合发行《中欧班列(义乌—马德里)》特种邮票1套2枚,它们的大小、形状相同(如图1)。邮票在设计时采用了多种数学元素:根据画面内容邮票以平行四边形的形式呈现,代表着列车前进的速度,凸显中欧班列的动态美;中国与西班牙两个列车图形保持对称,并向外延展,……;在单枚邮票票面上的平行四边形ABCD中,邻边AB与AD的长度比非常接近黄金分割数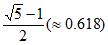 。
。
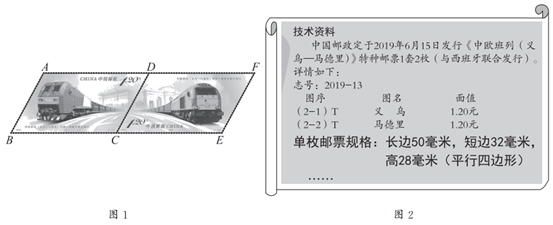
单枚邮票的规格见图2所示的技术资料(节选),设图1的平行四边形ABCD中BC边上的高为AH。
根据以上信息解决问题:
(1)提取信息:在平行四边形ABCD中,BC=________mm,AB=________mm,AH=_________mm;
(2)计算BH的长(结果用最简二次根式表示);
(3)如果将图1中的平行四边形ABCD设计成精确地满足相邻两边的比为黄金分割数,即在平行四边形ABCD中,满足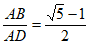 ,且
,且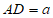 ,求此时2枚连印的邮票票面中平行四边形ABEF的周长(用含a的式子表示,结果用最简二次根式表示,无需计算近似值)。
,求此时2枚连印的邮票票面中平行四边形ABEF的周长(用含a的式子表示,结果用最简二次根式表示,无需计算近似值)。
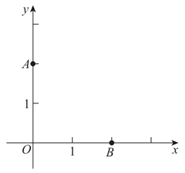
24. 在平面直角坐标系xOy中,A(0,2),B(2,0),四边形AOBC的第四个顶点C在第一象限,AC=1,BC=3。
(1)尺规作图:作出四边形AOBC(不要求写作法);
(2)求∠OAC的度数及四边形AOBC的面积。
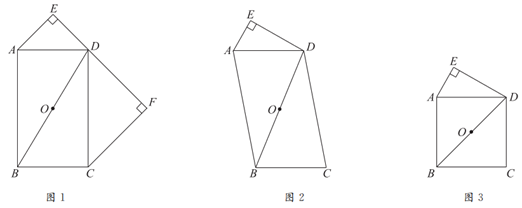
25. 在平行四边形ABCD中,O是对角线BD的中点,点E在平行四边形ABCD外,且∠AED=90°,过点C作直线ED的垂线,垂足为F,连接OE,OF。
(1)如图1,当平行四边形ABCD为矩形,且∠DAE=45°时,画出线段OE与OF,并直接写出这两条线段的数量关系;
(2)在图2中,根据题意补全图形,写出线段OE与OF的数量关系并加以证明;
(3)如图3,当平行四边形ABCD为正方形时,若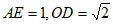 ,直接写出OF的长。
,直接写出OF的长。
附加题
试卷满分:20分
一、操作题(本题6分)
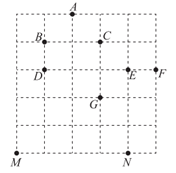
从下面正方形网格的格点A~N中,选择恰当的格点,分别画出以所选择格点为顶点的以下图形,并用字母表示。
①矩形;②菱形;③既不是矩形也不是菱形的平行四边形。
二、方案比较(本题6分)
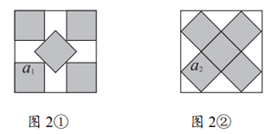
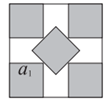
在边长为1的正方形中放置5个大小相同的小正方形,现在有如下两个放置方案(这两个方案中小正方形的边长分别为a1,a2):
图形 | 边长满足的条件 | 边长的值 | |
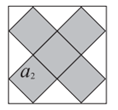
方案一 |
|
|
|
方案二 |
| ①_________ | ② |
(1)补全表格;
(2)比较a1与a2的大小关系并说明理由。
三、解答题(本题8分)
对于平面内三点M,N,P,我们规定:若将点M绕点P顺时针旋转α(0°<α<360°)后能与点N重合,就将其简记为: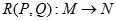 。
。
在平面直角坐标系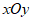 中,
中,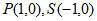 。
。
解决下面的问题:
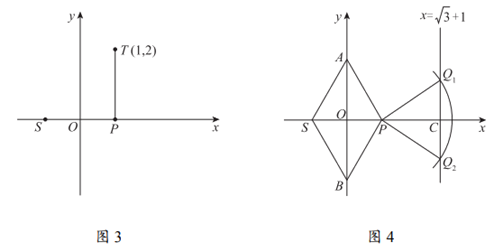
(1)如图1,若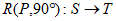 ,画出点T并直接写出点T的坐标;
,画出点T并直接写出点T的坐标;
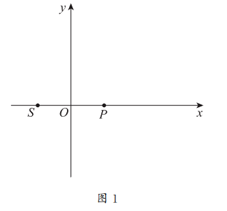
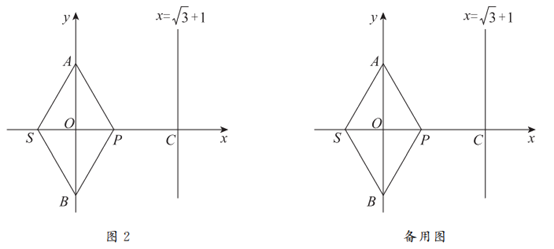
(2)如图2,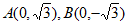 ,直线
,直线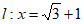 与x轴的交点为C。
与x轴的交点为C。
①若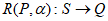 ,且点Q落在直线
,且点Q落在直线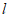 上,求
上,求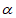 的值;
的值;
②若点E在四边形ASBP的边上运动,在直线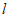 上存在相应的点F,使得
上存在相应的点F,使得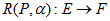 ,请直接写出点E的横坐标
,请直接写出点E的横坐标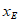 的取值范围。
的取值范围。
【试题答案】
一、选择题(本题共30分,每小题3分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | B | C | C | B | D | D | B | D | A | A |
二、填空题(本题共26分,其中第18题5分,其余每小题3分)
11. 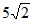 12. 60 13. -6 14. 10 15. 1 16. 8
12. 60 13. -6 14. 10 15. 1 16. 8
17. 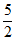 或
或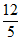
18. (1)见图1(2分);
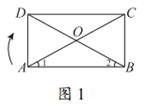
(2)①(1分),对角线相等的平行四边形是矩形(答案不唯一)(2分)
三、解答题(本题共44分,第19~23题每小题6分,第24、25题每小题7分)
19. 解:(1)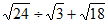
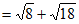
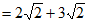 2分
2分
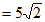 。 3分
。 3分
(2)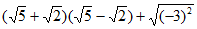
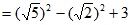 2分
2分
=5-2+3
=6。 3分
20. 解: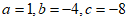 。 1分
。 1分
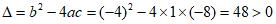 。 2分
。 2分
方程有两个不相等的实数根
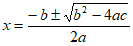 3分
3分
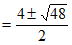
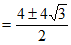 4分
4分
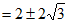 。
。
所以,原方程的根为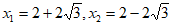 。 6分
。 6分
21. (1)证明:如图2。
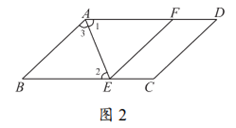
∵平行四边形ABCD,
∴AD∥BC,
∴∠1=∠2,
∵EF∥AB,
∴四边形ABEF是平行四边形, 2分
∵AE平分∠BAD,
∴∠1=∠3,
∴∠2=∠3,
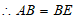 , 3分
, 3分
∴四边形ABEF是菱形。 4分
(2)点P与点E重合,3。 6分
22. 解:(1)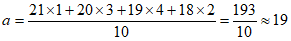 (岁)。 1分
(岁)。 1分
(2)①19; 2分
②19; 3分
③19,20,21。 5分
(3)20。 6分
23. 解:(1)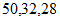 。 3分
。 3分
(2)如图3。
在Rt△ABH中,∠AHB=90°,
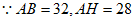 ,
,
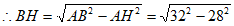
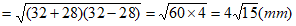 。 4分
。 4分
(3)C平行四边形ABEF=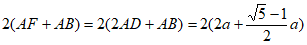
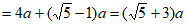 。 6分
。 6分
24. 解:(1)作图见图4(分别以A,B为圆心,1,3为半径作弧,两弧在第一象限交于点C, 1分
(2)如图4,连接AB。
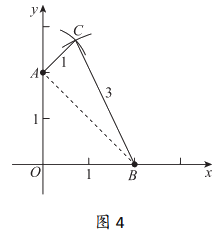
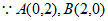 ,
,
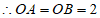 。 2分
。 2分
在Rt△AOB中,∠AOB=90°,
∴∠OAB=45°,
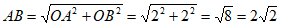 。 3分
。 3分
∵在△ABC中,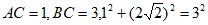 ,
,
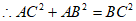 , 4分
, 4分
∴△ABC是直角三角形,∠BAC=90°, 5分
∴∠OAC=∠OAB+∠BAC=45°+90°=135°, 6分
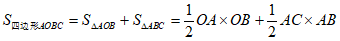
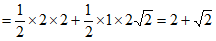 。 7分
。 7分
25. 解:(1)作图见图5,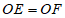 。 1分
。 1分
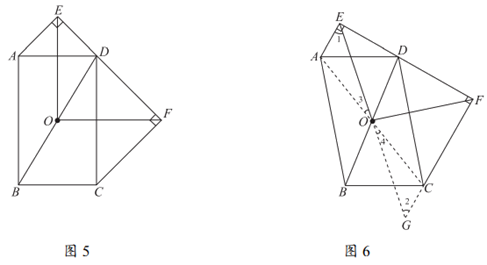
(2)作图见图6。 2分
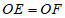 。 3分
。 3分
证明:连接AC,延长EO,FC,两条延长线交于点G,
∵平行四边形ABCD,O是对角线BD的中点,
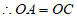 , 4分
, 4分
∵CF⊥EF,
∴∠CFE=90°,
∵∠AED=90°,
∴∠CFE+∠AED=180°,
∴CF∥AE,
∴∠1=∠2。
在△OAE与△OCG中,
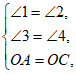
∴△OAE≌△OCG,
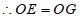 。 5分
。 5分
在Rt△EFG中,∠EFG=90°,OF为斜边EG的中线,
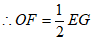 ,
,
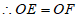 。 6分
。 6分
(3)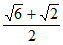 。 7分
。 7分
附加题答案
一、操作题(本题6分)
解:画图见图1。
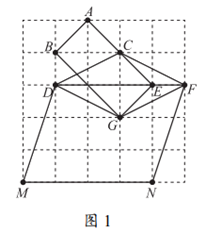
①矩形ABGE;②菱形CDGF;③既不是矩形也不是菱形的平行四边形DMNF。
二、方案比较(本题6分)
解:(1)①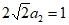 ; 2分
; 2分
②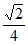 。 3分
。 3分
(2)
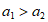 。 4分
。 4分
理由如下:
方法1:如图2,方案一中,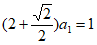 ;方案二中,
;方案二中,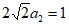 ,
,
又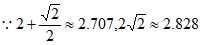 ,
,
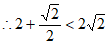 。
。
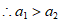 。 6分
。 6分
方法2: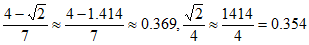 ,
,
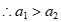 。
。
方法3:计算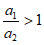 ,可得
,可得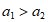 。
。
三、解答题(本题8分)
解:(1)画图见图3。 1分
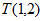 。 2分
。 2分
(2)①如图4,以点P为圆心,PS为半径作弧,交直线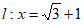 于点
于点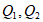 ,连接
,连接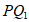 ,
,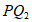 ,则∠PCQ1=90°,
,则∠PCQ1=90°,
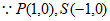 ,
,
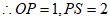 ,
,
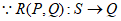 ,
,
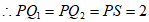 ,
,
∵直线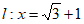 与x轴的交点为C,
与x轴的交点为C,
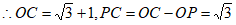 。
。
在Rt△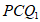 中,∠
中,∠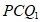 =90°,
=90°,
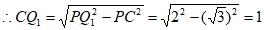 。
。
在△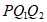 中,
中,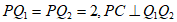 ,
,
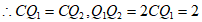 ,
,
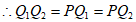 ,△
,△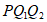 为等边三角形,∠
为等边三角形,∠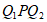 =60°,
=60°,
∴∠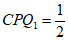 ∠
∠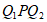 =30°。
=30°。
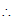 ∠
∠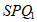 =180° – ∠
=180° – ∠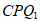 =180°-30°=150°, 5分
=180°-30°=150°, 5分
∠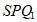 +∠
+∠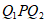 =150°+60°=210°, 6分
=150°+60°=210°, 6分
∴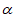 =150°或210°。
=150°或210°。
②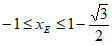 。 8分
。 8分

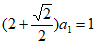
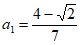
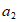 =________
=________