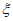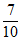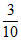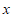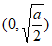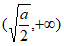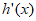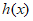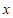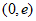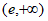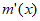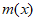本试卷满分为150分,考试时间为120分钟
第一部分 (选择题 共40分)
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 设集合P={1,2,3,4},Q={x||x|≤3,x∈R},则P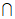 Q等于
Q等于
A. {1} B. {1,2,3}
C. {3,4} D. {-3,-2,-1,0,1,2,3}
2. 在复平面内,复数5+6i,3-2i对应的点分别为A,B。若C为线段AB的中点,则点C对应的复数是
A. 8+4i B. 2+8i C. 4+2i D. 1+4i
3. 下列函数中,既是奇函数又在区间(0,+∞)上单调递减的是
A. 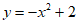 B.
B.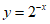
C. 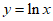 D.
D.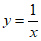
4. 圆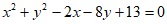 的圆心到直线
的圆心到直线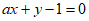 的距离为1,则a=
的距离为1,则a=
A. –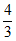 B. –
B. –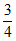 C.
C. 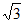 D. 2
D. 2
5. 将4位志愿者分配到博物馆的3个不同场馆服务,每个场馆至少1人,不同的分配方案有( )种
A. 36 B. 64 C. 72 D. 81
6. 如图,网格纸的小正方形的边长是1,粗线表示一正方体被某平面截得的几何体的三视图,则该几何体的体积为
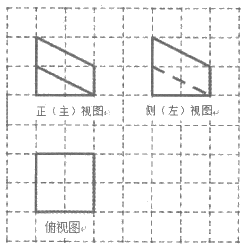
A. 2 B. 4 C. 5 D. 8
7. 函数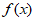 =
=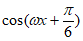 (
(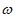 >0)的最小正周期为
>0)的最小正周期为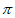 ,则
,则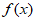 满足
满足
A. 在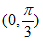 上单调递增 B. 图象关于直线x=
上单调递增 B. 图象关于直线x=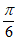 对称
对称
C. 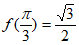 D. 当
D. 当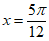 时有最小值-1
时有最小值-1
8. 设{an}是等差数列,其前n项和为Sn。则”S1+S3>2 S2“是”{an}为递增数列”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
9. 设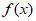 是定义在R上的函数,若存在两个不等实数x1,x2∈R,使得
是定义在R上的函数,若存在两个不等实数x1,x2∈R,使得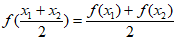 ,则称函数
,则称函数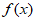 具有性质P,那么下列函数:
具有性质P,那么下列函数:
①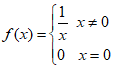 ;②
;②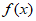 =
=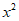 ③
③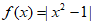 ;
;
具有性质P的函数的个数为
A. 0 B. 1 C. 2 D. 3
10. 点M,N分别是棱长为2的正方体ABCD-A1B1C1D1中棱BC,CC1的中点,动点P在正方形BCC1B1 (包括边界)内运动。若PA1∥面AMN,则PA1的长度范围是
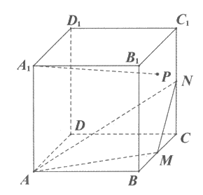
A. 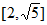 B.
B.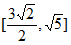
C. 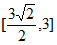 D.
D.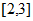
第二部分 (非选择题 共110分)
二、填空题共5小题,每小题5分,共25分。
11. 已知向量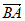 =
=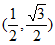 ,
,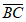 =
=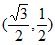 ,则∠ABC=_________。
,则∠ABC=_________。
12. 已知各项为正数的等比数列{an}中,a1=1,其前n项和为Sn(n∈N*),且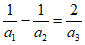 ,则
,则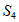 =__________。
=__________。
13. 能够说明”设a,b是任意非零实数,若”a>b,则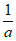 <
<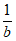 “是假命题的一组整数a,b的值依次为__________。
“是假命题的一组整数a,b的值依次为__________。
14. 已知F是抛物线C: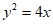 的焦点,M是C上一点,FM的延长线交y轴于点N。若M为FN的中点,则|FN|=__________。
的焦点,M是C上一点,FM的延长线交y轴于点N。若M为FN的中点,则|FN|=__________。
15. 石景山区为了支援边远山区的教育事业,组织了一支由13名一线中小学教师组成的支教团队,记者采访其中某队员时询问这个团队的人员构成情况,此队员回答:①有中学高级教师;②中学教师不多于小学教师;③小学高级教师少于中学中级教师;④小学中级教师少于小学高级教师;⑤支教队伍的职称只有小学中级、小学高级、中学中级、中学高级;⑥无论是否把我计算在内,以上条件都成立。由此队员的叙述可以推测出他的学段及职称分别是________、_________。
三、解答题共6小题,共85分。解答应写出文字说明,演算步骤或证明过程。
16. (本小题14分)
如图,在正四棱锥P-ABCD中,AB=PB=2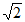 ,AC
,AC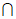 BD=O。
BD=O。
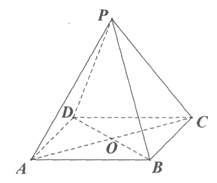
(I)求证:BO⊥面PAC;
(II)求二面角A-PC-B的余弦值。
17. (本小题14分)
2020年,北京将实行新的高考方案。新方案规定:语文、数学和英语是考生的必考科目,考生还需从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目。若一个学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定。例如,学生甲选择”物理、化学和生物”三个选考科目,则学生甲的选考方案确定,”物理、化学和生物”为其选考方案。
某校为了解高一年级840名学生选考科目的意向,随机选取60名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有16人 | 16 | 16 | 8 | 4 | 2 | 2 |
选考方案待确定的有12人 | 8 | 6 | 0 | 2 | 0 | 0 | |
女生 | 选考方案确定的有20人 | 6 | 10 | 20 | 16 | 2 | 6 |
选考方案待确定的有12人 | 2 | 8 | 10 | 0 | 0 | 2 |
(I)估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?
(II)从选考方案确定的16名男生中随机选出2名,求恰好有一人选”物理、化学、生物”的概率;
(III)从选考方案确定的16名男生中随机选出2名,
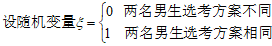 ,求
,求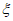 的分布列和期望。
的分布列和期望。
18. (本小题14分)
已知锐角△ABC,同时满足下列四个条件中的三个:
①A=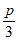 ②a=13 ③c=15 ④sinC=
②a=13 ③c=15 ④sinC=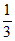
(I)请指出这三个条件,并说明理由;
(II)求△ABC的面积。
19. (本小题15分)
已知椭圆C: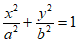 (a>b>0)的右焦点为F(1,0),离心率为
(a>b>0)的右焦点为F(1,0),离心率为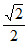 。直线l过点F且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M。
。直线l过点F且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M。
(I)求椭圆C的方程;
(II)证明:直线OM的斜率与l的斜率的乘积为定值;
(III)延长线段OM与椭圆C交于点P,若四边形OAPB为平行四边形,求此时直线l的斜率。
20. (本小题14分)
已知函数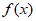 =
=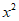 (x>0),g(x)=alnx(a>0)。
(x>0),g(x)=alnx(a>0)。
(I)若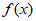 >
>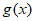 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(II)当a=1时,过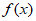 上一点(1,1)作
上一点(1,1)作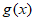 的切线,判断:可以作出多少条切线,并说明理由。
的切线,判断:可以作出多少条切线,并说明理由。
21. (本小题14分)
有限个元素组成的集合A={a1,a2,…,an},n∈N*,记集合A中的元素个数为card(A),即card(A)=n。定义A+A={x+y|x∈A,y∈A},集合A+A中的元素个数记为card(A+A),当card(A+A)=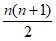 时,称集合A具有性质P。
时,称集合A具有性质P。
(I)A={1,4,7},B={2,4,8),判断集合A,B是否具有性质P,并说明理由;
(II)设集合A={a1,a2,a3,2020},a1< a2< a3<2020且ai∈N*(i=1,2,3),若集合A具有性质P,求a1+ a2+ a3的最大值;
(III)设集合A={ a1,a2,…,an},其中数列{ an}为等比数列,ai>0(i=1,2,…,n)且公比为有理数,判断集合A是否具有性质P并说明理由。
参考答案
一、选择题:本大题共10个小题,每小题4分,共40分。
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | B | C | D | A | A | B | D | C | C | B |
二、填空题:本大题共5个小题,每小题5分,共25分。
11. 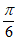 ; 12. 15; 13. 2,-1;答案不唯一
; 12. 15; 13. 2,-1;答案不唯一
14. 3; 15. 小学中级
三、解答题:本大题共6个小题,共85分。解答题应写出文字说明,证明过程或演算步骤。
16. (本小题14分)
(I)证明:联结PO。
在正四棱锥P-ABCD中,
PO⊥底面ABCD。
因为BO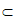 平面ABCD,
平面ABCD,
所以PO⊥BO。 …………3分
在正方形ABCD中,BO⊥AC,
又因为PO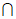 AC=O,
AC=O,
所以BO⊥面PAC。 …………6分
(II)解:由(I)知,PO,AO,BO两两垂直,
以O为坐标原点建立如图所示空间直角坐标系, ………7分
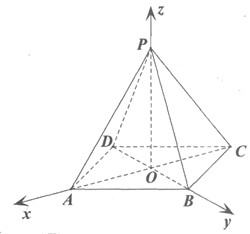
在正方形ABCD中,因为AB=2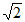 ,
,
所以AO=2。
又因为PB=2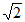 。
。
所以PO=2。
所以点P的坐标为P(0,0,2),点C的坐标为C(-2,0,0),
点B的坐标为B(0,2,0)。 …………8分
则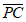 =(-2,0,-2),
=(-2,0,-2),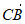 =(2,2,0)。 …………9分
=(2,2,0)。 …………9分
由(I)知,BO⊥平面PAC。
所以平面PAC的一个法向量为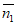 =
=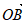 =(0,2,0)。 …………10分
=(0,2,0)。 …………10分
设平面PBC的一个法向量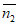 =(x,y,z)。
=(x,y,z)。
则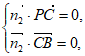 即
即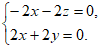
令y=1,则x=-1,z=1。
故平面PBC的一个法向量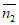 =(-1,1,1)。 …………13分
=(-1,1,1)。 …………13分
cos<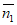 ,
,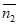 >
>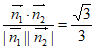
所以二面角A-PC-B的余弦值为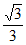 。 …………14分
。 …………14分
17. (本小题14分)
解:(I)由数据知,60人中选考方案确定的学生中选考生物的学生有8+20=28人…1分
所以该学校高一年级选考方案确定的学生中选考生物的学生有
840×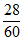 =392人 ………4分
=392人 ………4分
(II)选考方案确定且为”物理,化学,生物”的男生共有8人。 ……5分
设”恰好有一人选物理、化学、生物”为事件A ……6分
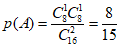 …8分
…8分
(III)由数据可知,选考方案确定的男生中有8人选择物理、化学和生物;有4人选择物理、化学和历史;有2人选择物理、化学和地理;有2人选择物理、化学和政治。 ……9分
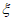 的可能取值为0,1。
的可能取值为0,1。
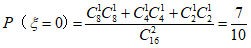
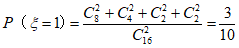 ……12分
……12分
所以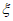 的分布列为:
的分布列为:
| 0 | 1 |
P |
|
|
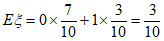 ……14分
……14分
18. (本小题14分)
解:(I)△ABC同时满足①,②,③。 …………3分
理由如下:
若△ABC同时满足①,④,则在锐角△ABC中,
sinC=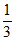 <
<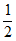 ,所以0<C<
,所以0<C<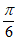
又因为A=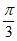 ,所以
,所以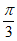 <A+C<
<A+C<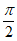
所以B>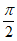 ,这与△ABC是锐角三角形矛盾,
,这与△ABC是锐角三角形矛盾,
所以△ABC不能同时满足①,④, …………6分
所以△ABC同时满足②,③。 …………7分
因为c>a所以C>A若满足④
则A<C<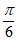 ,则B>
,则B>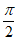 ,这与△ABC是锐角三角形矛盾
,这与△ABC是锐角三角形矛盾
故△ABC不满足④。 …………9分
故△ABC满足①,②,③。
(II)因为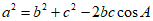 , …………10分
, …………10分
所以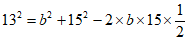 。
。
解得b=8或b=7。 …………12分
当b=7时,cosC=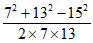 <0
<0
所以C为钝角,与题意不符合,所以b=8。 …………13分
所以△ABC的面积S=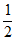 bcsinA=30
bcsinA=30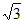 。 …………14分
。 …………14分
19. (本小题15分)
解:(I)由已知c=1,e=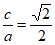 , …………2分
, …………2分
又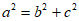 ,解得
,解得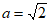 ,b=1 …………4分
,b=1 …………4分
所以椭圆方程为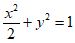 。 …………5分
。 …………5分
(II)设直线l的方程为y=k(x-1)(k≠0)
联立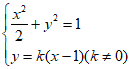 消去y得
消去y得
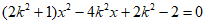 ,不妨设
,不妨设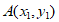 ,
,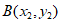 ……7分
……7分
则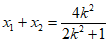 ,因为M为线段AB的中点
,因为M为线段AB的中点
所以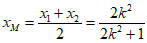 ,
,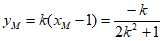 ……8分
……8分
所以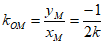 ……9分
……9分
所以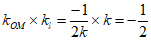 为定值。 ……10分
为定值。 ……10分
(III)若四边形OAPB为平行四边形,则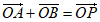 …………12分
…………12分
所以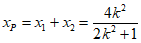
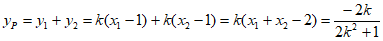 ……13分
……13分
因为点P在椭圆上,所以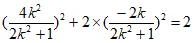 …14分
…14分
解得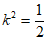 即
即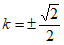
所以当四边形OAPB为平行四边形时,直线l的斜率为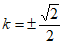 。 ………15分
。 ………15分
20. (本小题14分)
解:(I)令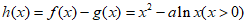 …………1分
…………1分
所以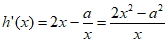
令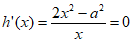 ,解得
,解得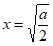 。 ……3分
。 ……3分
当x变化时,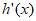 ,
,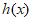 的变化情况如下表:
的变化情况如下表:
|
|
|
|
| – | 0 | + |
| 减 | 极小值 | 增 |
…………5分
所以在(0,+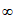 )的最小值为
)的最小值为 …6分
…6分
令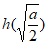 >0 解得0<a<2e。
>0 解得0<a<2e。
所以当0<a<2e时,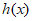 >0恒成立,即
>0恒成立,即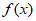 >
>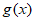 恒成立。 ………7分
恒成立。 ………7分
(II)可作出2条切线。 …………8分
理由如下:当a=1时,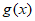 =lnx。
=lnx。
设过点(1,1)的直线l与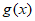 =lnx相切于点P(
=lnx相切于点P(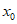 ,
,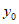 ), …………9分
), …………9分
则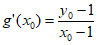 即
即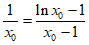
整理得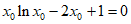 …………10分
…………10分
令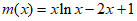 ,则
,则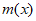 在(0,+
在(0,+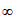 )上的零点个数与切点P的个数一一对应。
)上的零点个数与切点P的个数一一对应。
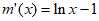 ,令
,令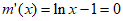 解得x=e。 …………11分
解得x=e。 …………11分
当x变化时,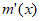 ,
,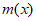 的变化情况如下表:
的变化情况如下表:
|
| e |
|
| – | 0 | + |
| 减 | 极小值 | 增 |
所以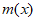 在(0,e)上单调递减,在(e,+
在(0,e)上单调递减,在(e,+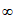 )上单调递增。
)上单调递增。
且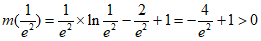
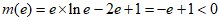
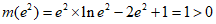 ………13分
………13分
所以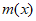 在(
在(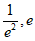 )和(
)和(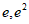 )上各有一个零点,即
)上各有一个零点,即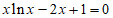 有两个不同的解。
有两个不同的解。
所以过点(1,1)可作出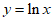 的2条切线。 …………14分
的2条切线。 …………14分
21. (本小题14分)
解:(I)集合A不具有性质P,集合B具有性质P。
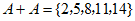 ,
,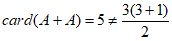 不具有性质P;
不具有性质P;
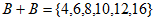 ,
,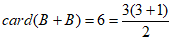 ,具有性质P。………3分
,具有性质P。………3分
(II)若三个数a,b,c成等差数列,则A={a,b,c}不具有性质P,理由是a+c=2b。
因为a1< a2< a3<2020且ai∈N*(i=1,2,3)所以a3≤2019,
要使a1+ a2+ a3取最大,则a3=2019;
a2≤2018,易知{2018,2019,2020}不具有性质P,要使a1+ a2+ a3取最大,
则a2=2017;
a1≤2016,要使a1+ a2+ a3取最大,检验可得a1=2014;
(a1+ a2+ a3)max=6050 …………8分
(III)集合A具有性质P。
设等比数列的公比为q,所以an= a1qn-1(a1>0)且q为有理数,
假设当i<k≤l<j时有ai+ aj= ak+ al成立,则有
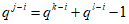 ………10分
………10分
因为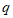 为有理数,设
为有理数,设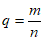 (m,n∈N*)且(m,n互质),因此有
(m,n∈N*)且(m,n互质),因此有
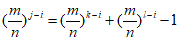 即
即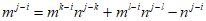 (1),
(1),
(1)式左边是m的倍数,右边是n的倍数,又m,n互质,
显然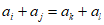 不成立。 ……12分
不成立。 ……12分
所以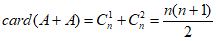 ,所以集合A具有性质P。 ……14分
,所以集合A具有性质P。 ……14分