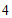本试卷共三道大题,28道小题.满分100分,考试时间120分钟.
一、选择题(本题共16分,每小题2分)
下面各题均有四个选项,符合题意的选项只有一个.
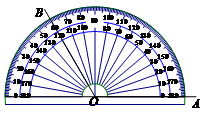
1.如图,用量角器度量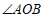 ,可以读出
,可以读出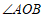 的度数为
的度数为
A. C. | B. D. |
2.花粉的质量很小,一粒某种植物花粉的质量约为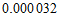 毫克,将
毫克,将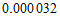 用科学记数法表示应为
用科学记数法表示应为
A. C. | B. D. |
3.下图是某个几何体的三视图,则该几何体是

A.圆锥 | B.长方体 |
C.三棱柱 | D.圆柱 |
4.实数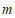 ,
,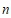 在数轴上的对应点的位置如图所示,则正确的结论是
在数轴上的对应点的位置如图所示,则正确的结论是
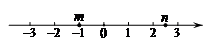
A. | B. | C. | D. |
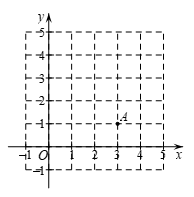
5.如图,小石同学在正方形网格图中建立平面直角坐标系后,点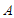 的坐标为
的坐标为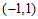 ,点
,点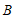 的坐标为
的坐标为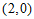 ,则点
,则点 的坐标为
的坐标为
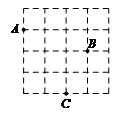
A. C. | B. D. |
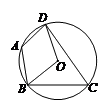
6. 如图,四边形 是⊙
是⊙ 的内接四边形,
的内接四边形,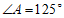 ,则
,则 的度数为
的度数为
A. C. | B. D. |
7.某厂的四台机床同时生产直径为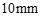 的零件,为了了解产品质量,质量检验员从这四台机床生产的零件中分别随机抽取
的零件,为了了解产品质量,质量检验员从这四台机床生产的零件中分别随机抽取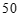 件产品,经过检测、整理、描述与分析,得到结果如下(单位:
件产品,经过检测、整理、描述与分析,得到结果如下(单位: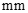 ):
):
机床数 特征 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 9.99 | 9.99 | 10.00 | 0.02 |
乙 | 9.99 | 10.00 | 10.00 | 0.07 |
丙 | 10.02 | 10.01 | 10.00 | 0.02 |
丁 | 10.02 | 9.99 | 10.00 | 0.05 |
从样本来看,生产的零件直径更接近标准要求且更稳定的机床是
A.甲 | B.乙 | C.丙 | D.丁 |
8.下图反映了我国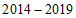 年快递业务量(单位:亿件)及年增长率(%)的情况
年快递业务量(单位:亿件)及年增长率(%)的情况
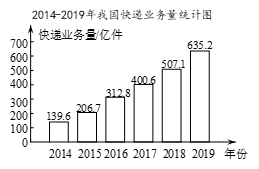
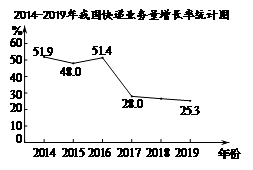
(以上数据来源于国家统计局网站)
根据统计图提供的信息,下列推断不合理的是
A. B.与 |
C. D. |
二、填空题(本题共16分,每小题2分)
9.如果分式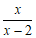 有意义,那么
有意义,那么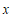 的取值范围是______.
的取值范围是______.
10.如果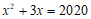 ,那么代数式
,那么代数式 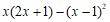 的值为______.
的值为______.
11.如图, 是⊙
是⊙ 的直径,点
的直径,点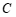 是⊙
是⊙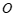 上一点,
上一点,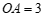 ,
,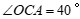 ,则阴影部分的面积为______.
,则阴影部分的面积为______.
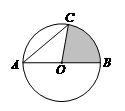
12.如图 ,边长为
,边长为 的大正方形中有一个边长为
的大正方形中有一个边长为 的小正方形,若将图
的小正方形,若将图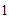 中的阴影部分拼成一个矩形如图
中的阴影部分拼成一个矩形如图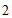 ,比较两图中阴影部分的面积,写出一个正确的等式:______.
,比较两图中阴影部分的面积,写出一个正确的等式:______.
13.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中第七卷《盈不足》记载了一道有趣的数学问题:”今有大器五、小器一容三斛;大器一、小器五容二斛. 问大、小器各容几何?”
译文:”今有大容器5个,小容器1个,总容量为3斛;大容器1个,小容器5个,
总容量为2斛.问大容器、小容器的容量各是多少斛?”
(注:斛,音hú,是古代的一种容量单位)
设大容器的容量为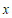 斛,小容器的容量为
斛,小容器的容量为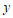 斛,根据题意,可列方程组为____.
斛,根据题意,可列方程组为____.
14.某种黄豆在相同条件下的发芽试验,结果如下表所示:
试验粒数n | 500 | 1000 | 2000 | 4000 | 7000 | 10000 | 12000 | 15000 |
发芽的粒数m | 421 | 868 | 1714 | 3456 | 6020 | 8580 | 10308 | 12915 |
发芽的频率 | 0.842 | 0.868 | 0.857 | 0.864 | 0.860 | 0.858 | 0.859 | 0.861 |
估计该种黄豆发芽的概率为______(精确到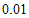 ).
).
15.在平面直角坐标系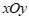 中,点
中,点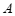 的坐标为
的坐标为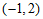 ,点
,点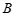 的坐标为
的坐标为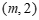 ,若直线
,若直线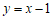 与线段
与线段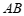 有公共点,则
有公共点,则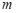 的值可以为______(写出一个即可).
的值可以为______(写出一个即可).
16.正方形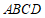 中,点
中,点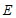 在边
在边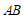 上,
上,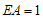 ,
,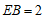 ,将线段
,将线段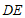 绕点
绕点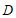 逆时针旋转,使点
逆时针旋转,使点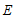 落在直线
落在直线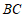 上的点
上的点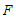 处,则
处,则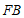 的长度为______.
的长度为______.
三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27-28题,每小题7分)解答应写出文字说明、演算步骤或证明过程.
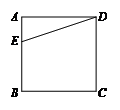
17.计算: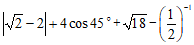 .
.
18.解不等式组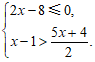
19.关于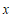 的一元二次方程
的一元二次方程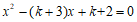 .
.
(1)求证:方程总有两个实数根;
(2)若方程有一个根为负数,求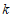 的取值范围.
的取值范围.
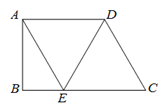
20.如图,在四边形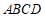 中,
中,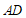 ∥
∥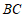 ,
,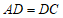 ,
,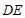 平分
平分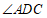 交
交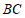 于点
于点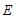 ,连接
,连接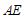 .
.
(1)求证:四边形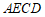 是菱形;
是菱形;
(2)连接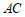 交
交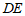 于点
于点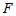 .若
.若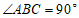 ,
,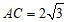 ,
,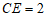 ,求
,求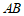 的长.
的长.
21.在抗击新冠肺炎疫情期间,老百姓越来越依赖电商渠道获取必要的生活资料.小石经营的水果店也适时加入了某电商平台,并对销售的水果中的部分(如下表)进行促销:参与促销的水果免配送费且一次购买水果的总价满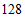 元减
元减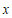 元.每笔订单顾客网上支付成功后,小石会得到支付款的
元.每笔订单顾客网上支付成功后,小石会得到支付款的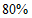 .
.
(1)当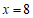 时,某顾客一次购买苹果和车厘子各
时,某顾客一次购买苹果和车厘子各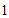 箱,需要支付______元,小石会得到______元;
箱,需要支付______元,小石会得到______元;
(2)在促销活动中,为保障小石每笔订单所得到的金额不低于促销前总价的七折,则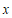 的最大值为______.
的最大值为______.
参与促销水果 | |
水 果 | 水 果 |
苹果 | 苹果 |
耙耙柑 | 耙耙柑 |
车厘子 | 车厘子 |
火龙果 | 火龙果 |
22.如图,在平面直角坐标系 中,函数
中,函数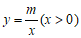 的图象
的图象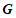 经过点
经过点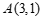 ,直线
,直线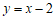 与
与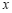 轴交于点
轴交于点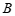 .
.
(1)求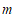 的值及点
的值及点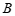 的坐标;
的坐标;
(2)直线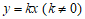 与函数
与函数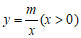 的图象
的图象 交于点
交于点 ,记图象
,记图象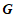 在点
在点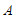 ,
,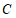 之间的部分与线段
之间的部分与线段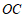 ,
,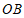 ,
,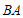 围成的区域(不含边界)为
围成的区域(不含边界)为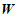 .
.
①当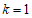 时,直接写出区域
时,直接写出区域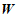 内的整点个数;
内的整点个数;
②若区域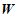 内恰有
内恰有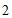 个整点,结合函数图象,求
个整点,结合函数图象,求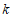 的取值范围.
的取值范围.
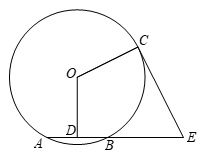
23.如图,点 ,
, ,
, 在⊙
在⊙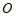 上,
上,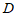 是弦
是弦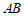 的中点,点
的中点,点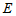 在
在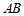 的延长线上,连接
的延长线上,连接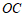 ,
,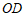 ,
,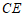 ,
,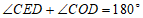 .
.
(1)求证: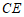 是⊙
是⊙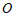 切线;
切线;
(2)连接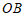 ,若
,若 ∥
∥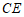 ,
,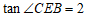 ,
,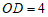 ,求
,求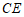 的长.
的长.
24.经过多方努力,北京市 年在区域空气质量同步改善、气象条件较常年整体有利的情况下,大气环境中细颗粒物(
年在区域空气质量同步改善、气象条件较常年整体有利的情况下,大气环境中细颗粒物( )等四项主要污染物同比均明显改善.对北京市空气质量的有关数据进行收集、整理、描述与分析,下面给出了部分信息:
)等四项主要污染物同比均明显改善.对北京市空气质量的有关数据进行收集、整理、描述与分析,下面给出了部分信息:
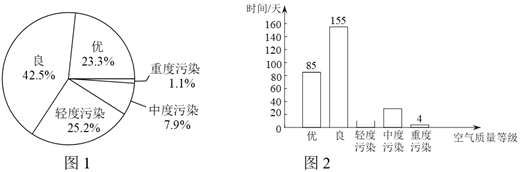
a.北京市 年空气质量各级别分布情况如下图(全年无严重污染日)(不完整):
年空气质量各级别分布情况如下图(全年无严重污染日)(不完整):
b.北京市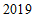 年大气环境中二氧化硫(
年大气环境中二氧化硫(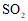 )的年均浓度为
)的年均浓度为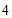 微克/立方米,稳定达到国家二级标准(
微克/立方米,稳定达到国家二级标准(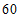 微克/立方米);
微克/立方米);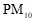 ,二氧化氮(
,二氧化氮(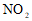 )的年均浓度分别为
)的年均浓度分别为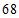 微克/立方米,
微克/立方米,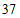 微克/立方米,均首次达到国家二级标准(
微克/立方米,均首次达到国家二级标准(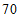 微克/立方米,
微克/立方米,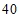 微克/立方米);
微克/立方米);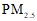 的年均浓度为
的年均浓度为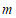 微克/立方米,仍是北京市大气主要污染物,超过国家二级标准(
微克/立方米,仍是北京市大气主要污染物,超过国家二级标准(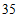 微克/立方米)的
微克/立方米)的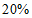 .
.
c.北京市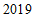 年大气环境中
年大气环境中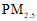 月均浓度变化情况如下:
月均浓度变化情况如下:
二氧化硫( )月均浓度(单位:微克/立方米)如下(不完整):
)月均浓度(单位:微克/立方米)如下(不完整):
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
月均浓度 | 9 | 6 | 5 | 4 | 3 | 2 | 3 | 3 | 5 | 4 |
(以上数据来源于北京市生态环境局官方网站)
根据以上信息,回答下列问题:
(1)北京市 年空气质量为”轻度污染”天数为( )
年空气质量为”轻度污染”天数为( )
A. | B. | C. |
(2)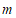 的值是______;
的值是______;
(3)北京市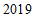 年大气环境中
年大气环境中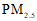 月均浓度达到国家二级标准的概率为____;
月均浓度达到国家二级标准的概率为____;
(4)北京市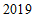 年大气环境中
年大气环境中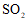 月均浓度的众数是
月均浓度的众数是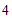 ,则中位数是______.
,则中位数是______.
25.如图,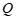 是
是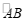 与弦
与弦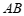 所围成图形的外部的一定点,
所围成图形的外部的一定点,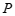 是弦
是弦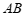 上的一动点,连接
上的一动点,连接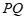 交
交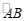 于点
于点 .已知
.已知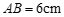 ,设
,设 ,
,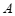 两点间的距离为
两点间的距离为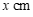 ,
,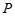 ,
,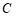 两点间的距离为
两点间的距离为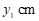 ,
,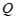 ,
,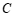 两点间的距离为
两点间的距离为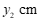 .
.
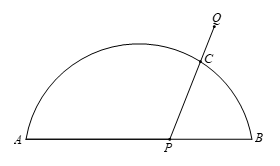
小石根据学习函数的经验,分别对函数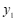 ,
,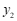 随自变量
随自变量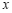 的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
(1)按照下表中自变量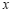 的值进行取点、画图、测量,分别得到了
的值进行取点、画图、测量,分别得到了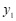 ,
,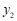 与
与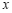 的几组对应值:
的几组对应值:
| 0 | 1 | 2 | 3 | 4 | 5 | 5.40 | 6 |
| 4.63 | 3.89 | 2.61 | 2.15 | 1.79 | 1.63 | 0.95 | |
| 1.20 | 1.11 | 1.04 | 0.99 | 1.02 | 1.21 | 1.40 | 2.21 |
(2)在同一平面直角坐标系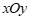 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点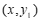 ,
,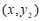 ,并画出函数
,并画出函数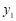 ,
,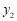 的图象;
的图象;
(3)结合函数图象,解决问题:当 为
为 的中点时,
的中点时,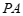 的长度约为____
的长度约为____ .
.
26.在平面直角坐标系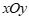 中,抛物线
中,抛物线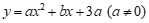 与
与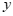 轴交于点
轴交于点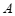 ,与
,与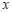 轴交于点
轴交于点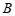 ,
,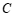 (点
(点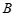 在点
在点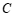 左侧).直线
左侧).直线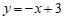 与抛物线的对称轴交于点
与抛物线的对称轴交于点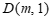 .
.
(1)求抛物线的对称轴;
(2)直接写出点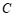 的坐标;
的坐标;
(3)点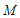 与点
与点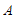 关于抛物线的对称轴对称,过点
关于抛物线的对称轴对称,过点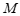 作
作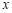 轴的垂线
轴的垂线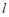 与直线
与直线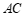 交于点
交于点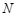 ,若
,若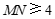 ,结合函数图象,求
,结合函数图象,求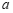 的取值范围.
的取值范围.
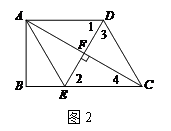
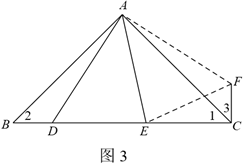
27.在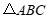 中,
中,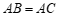 ,
, 是边
是边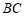 上的一点(不与点
上的一点(不与点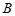 重合),边
重合),边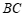 上点
上点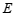 在点
在点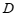 的右边且
的右边且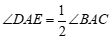 ,点
,点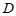 关于直线
关于直线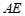 的对称点为
的对称点为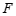 ,连接
,连接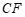 .
.
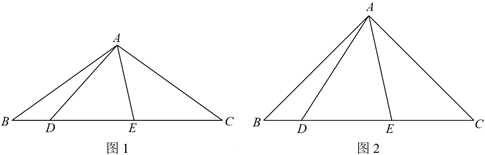
(1)如图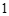 ,
,
①依题意补全图1;
②求证: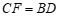 ;
;
(2)如图2,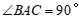 ,用等式表示线段
,用等式表示线段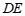 ,
,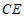 ,
,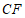 之间的数量关系,并证明.
之间的数量关系,并证明.
28.对于平面直角坐标系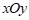 中的图形
中的图形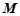 ,
,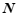 ,给出如下定义:
,给出如下定义: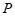 为图形
为图形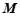 上任意一点,
上任意一点,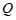 为图形
为图形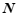 上任意一点,如果线段
上任意一点,如果线段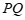 的长度有最小值,那么称这个最小值为图形
的长度有最小值,那么称这个最小值为图形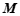 ,
,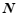 的”近距”,记作
的”近距”,记作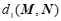 ;如果线段
;如果线段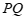 的长度有最大值,那么称这个最大值为图形
的长度有最大值,那么称这个最大值为图形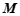 ,
,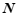 的”远距”,记作
的”远距”,记作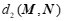 .已知点
.已知点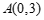 ,
,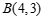 .
.
(1)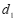 (点
(点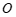 ,线段
,线段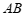 )= ______,
)= ______,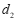 (点
(点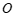 ,线段
,线段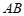 )= ______;
)= ______;
(2)一次函数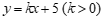 的图象与
的图象与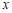 轴交于点
轴交于点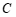 ,与
,与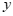 轴交于点
轴交于点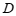 ,若
,若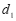 (线段
(线段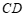 ,线段
,线段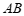 )
)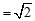 ,
,
①求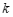 的值;
的值;
②直接写出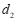 (线段
(线段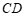 ,线段
,线段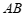 )= ______;
)= ______;
(3)⊙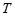 的圆心为
的圆心为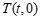 ,半径为
,半径为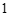 .若
.若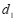 (⊙
(⊙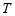 ,线段
,线段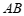 )
)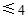 ,请直接写出
,请直接写出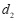 (⊙
(⊙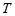 ,线段
,线段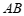 )的取值范围.
)的取值范围.

 【试题答案】
【试题答案】
一、选择题(本题共16分,每小题2分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | C | B | D | B | A | C | A | C |
二、填空题(本题共16分,每小题2分)
9. | 10. | 11. |
12. | 13. | 14. |
15.答案不唯一,如: | 16. | |
三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27-28题,每小题7分)解答应写出文字说明、演算步骤或证明过程.
17.解:原式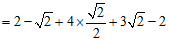 ………………………… 4分
………………………… 4分
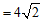 . …………………………… 5分
. …………………………… 5分
18.解:原不等式组为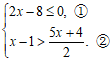
解不等式①,得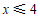 .
.
解不等式②,得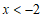 .…………………………………4分
.…………………………………4分
∴原不等式组的解集为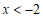 .…………………………………5分
.…………………………………5分
19.(1)证明:依题意,得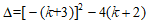 ……………………………1分
……………………………1分
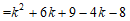
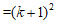 .…………………………………2分
.…………………………………2分
∵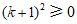 ,
,
∴方程总有两个实数根.…………………………………3分
(2)解:由求根公式,得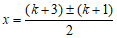 .
.
∴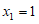 ,
,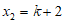 .…………………………………4分
.…………………………………4分
∵方程有一个根为负数,
∴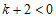 .
.
∴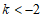 .
.
∴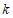 的取值范围是
的取值范围是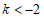 .…………………………………5分
.…………………………………5分
20.(1)证明:∵ ,如图1,
,如图1,
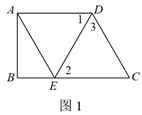
∴ .
.
∵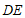 平分
平分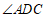 ,
,
∴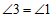 .
.
∴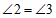 .
.
∴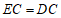 .
.
∵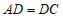
∴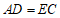 .
.
又∵ ,
,
∴四边形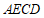 是平行四边形.
是平行四边形.
∴四边形 是菱形.…………………………………3分
是菱形.…………………………………3分
(2)解:∵四边形 是菱形,如图2,
是菱形,如图2,
∴ ,
,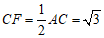 .
.
在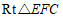 中,
中,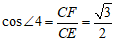 ,
,
∴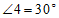 .
.
∵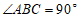 ,
,
∴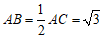 .…………………………………5分
.…………………………………5分
21.(1) ,
, ;…………………………………3分
;…………………………………3分
(2)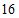 .…………………………………5分
.…………………………………5分
22.解:(1)∵函数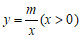 的图象
的图象 经过点
经过点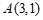
∴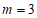 .…………………………………1分
.…………………………………1分
∵直线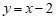 与
与 轴交于点
轴交于点 ,
,
∴点 的坐标为
的坐标为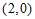 .…………………………………2分
.…………………………………2分
(2)① ;…………………………………3分
;…………………………………3分
②如图,
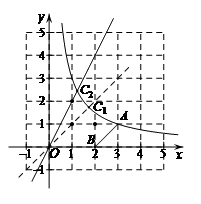
当直线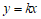 过点
过点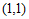 时,得
时,得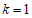 .
.
当直线 过点
过点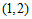 时,得
时,得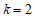 .
.
结合函数图象,可得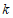 的取值范围是
的取值范围是
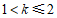 .…………5分
.…………5分
23.(1)证明:如图1,
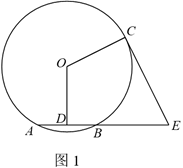
∵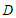 是弦
是弦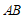 的中点,
的中点,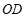 过圆心,
过圆心,
∴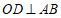
即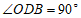 .
.
∵在四边形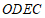 中,
中,
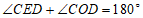 ,
,
∴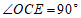 .
.
又∵ 是⊙
是⊙ 的半径,
的半径,
∴ 是⊙
是⊙ 切线.…………………………………2分
切线.…………………………………2分
(2)解:延长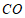 ,
,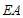 交于点
交于点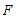 ,如图2.
,如图2.
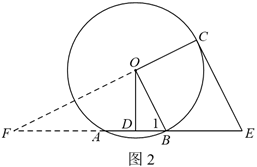
∵ ,
,
∴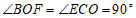 ,
,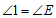 .
.
在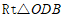 中,
中,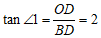 ,
, ,
,
∴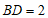 ,
,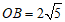 .…………………………………4分
.…………………………………4分
在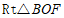 中,
中,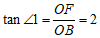 ,
,
∴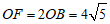 .
.
∵ ,
,
∴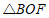 ∽
∽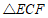
∴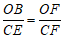
即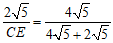
∴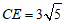 .…………………………………6分
.…………………………………6分
24.解:(1)B;…………………………………1分
(2)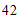 ;…………………………………3分
;…………………………………3分
(3)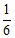 ;…………………………………4分
;…………………………………4分
(4)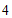 .…………………………………6分
.…………………………………6分
25.解:(1)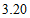 ;…………………………………2分
;…………………………………2分
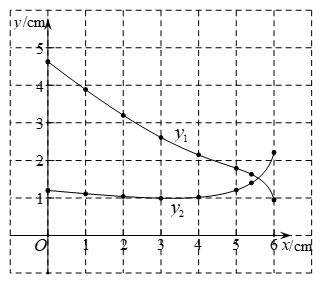 4分
4分
(2)
(3)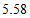 .…………………………………6分
.…………………………………6分
26.解:(1)∵直线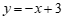 与抛物线的对称轴交于点
与抛物线的对称轴交于点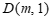 ,
,
∴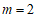 .
.
∴抛物线的对称轴为直线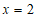 .…………………………………2分
.…………………………………2分
(2)点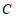 的坐标为
的坐标为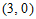 .…………………………………3分
.…………………………………3分
(3)∵抛物线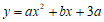 与
与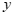 轴交于点
轴交于点 ,
,
∴点 的坐标为
的坐标为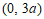 .
.
∵点 与点
与点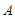 关于抛物线的对称轴对称,
关于抛物线的对称轴对称,
∴点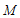 的坐标为
的坐标为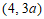 .
.
①当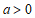 时,如图1.
时,如图1.
∵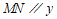 轴,
轴,
∴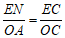 ,即
,即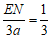 .
.
∴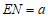 .
.
当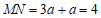 时,得
时,得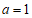 .
.
结合函数图象,若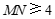 ,得
,得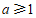 .……………………………5分
.……………………………5分
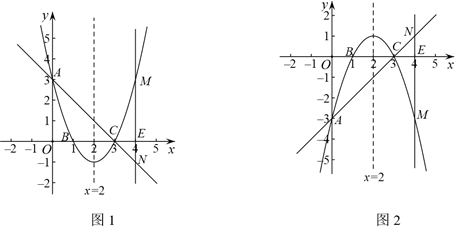
②当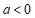 时,如图2.
时,如图2.
同理可得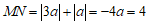 时,得
时,得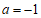 .
.
结合函数图象,若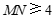 ,得
,得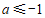 .
.
综上所述,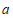 的取值范围是
的取值范围是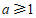 或
或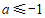 .…………………6分
.…………………6分
27.(1)①依题意补全图形,如图1.…………………………………1分
②证明:连接 ,如图2.
,如图2.
∵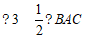 ,
,
∴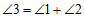 .
.
∵点 与点
与点 关于直线
关于直线 对称,
对称,
∴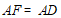 ,
,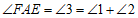 .
.
∴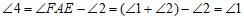 .
.
又∵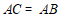 ,
,
∴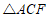 ≌
≌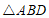 .
.
∴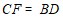 .…………………………………5分
.…………………………………5分
(2)线段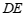 ,
,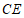 ,
,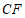 之间的数量关系是
之间的数量关系是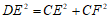 .
.
证明:连接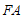 ,
,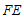 ,如图3.
,如图3.
∵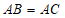 ,
,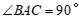 ,
,
∴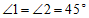 .
.
由(1)②,可得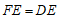 ,
,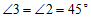 .
.
∴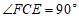 .
.
在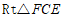 中,由勾股定理,得
中,由勾股定理,得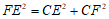 .
.
∴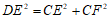 .…………………………………7分
.…………………………………7分
28.解:(1)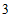 ,
,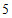 ;…………………………………2分
;…………………………………2分
(2)①过点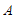 作
作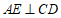 于点
于点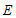 ,
,
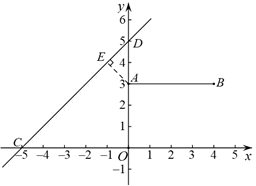
则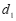 (线段
(线段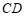 ,线段
,线段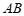 )
)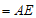
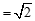 ,
,
∵直线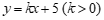 与
与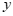 轴交点为
轴交点为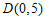 ,
,
与 轴交点
轴交点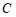 在
在 轴负半轴,
轴负半轴,
∴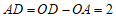 .
.
∴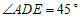 .
.
∴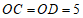 .
.
∴点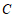 的坐标为
的坐标为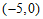 .
.
∴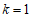 .…………………………………4分
.…………………………………4分
②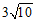 .…………………………………5分
.…………………………………5分
(3)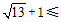
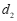 (⊙
(⊙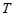 ,线段
,线段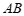 )
)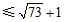 .……………………7分
.……………………7分

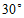
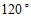
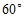
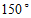
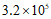
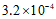
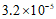
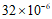
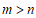

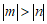
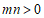
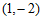
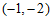
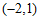
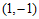
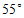
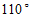
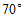
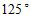
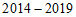 年,我国快递业务量的年平均值超过
年,我国快递业务量的年平均值超过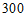 亿件
亿件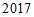 年相比,
年相比,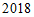 年我国快递业务量的增长率超过
年我国快递业务量的增长率超过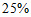
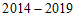 年,我国快递业务量与年增长率都是逐年增长
年,我国快递业务量与年增长率都是逐年增长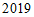 年我国的快递业务量比
年我国的快递业务量比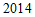 年的
年的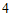 倍还多
倍还多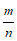
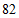
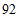
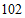
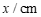
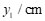
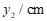
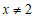
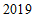
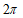
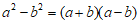
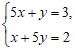
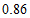
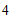 (
(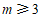 )
)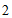 或
或