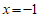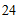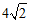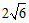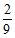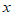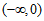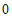本试卷共150分。考试时长120分钟。
第一部分 (选择题 共40分)
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 在复平面内,复数i(2-i)对应的点位于
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
2. 已知集合A={x|0<x<3},A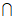 B={1},则集合B可以是
B={1},则集合B可以是
A. {l,2} B. {1,3}
C. {0,1,2} D. {l,2,3}
3. 已知双曲线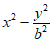 =1(b>0)的离心率为
=1(b>0)的离心率为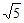 ,则b的值为
,则b的值为
A. 1 B. 2
C. 3 D. 4
4. 已知实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是
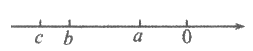
A. 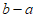 <
<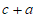 B.
B.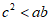
C. 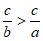 D.
D.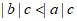
5. 在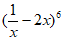 的展开式中,常数项为
的展开式中,常数项为
A. -120 B. 120
C. -160 D. 160
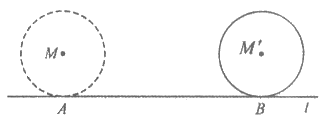
6. 如图,半径为1的圆M与直线l相切于点A,圆M沿着直线l滚动。当圆M滚动到圆M’时,圆M’与直线l相切于点B,点A运动到点A’,线段AB的长度为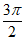 ,则点M’到直线BA’的距离为
,则点M’到直线BA’的距离为
A. 1 B. 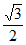 C.
C. 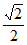 D.
D.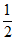
7. 已知函数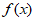 =|
=|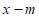 |与函数
|与函数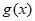 的图象关于y轴对称。若
的图象关于y轴对称。若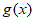 在区间(1,2)内单调递减,则m的取值范围为
在区间(1,2)内单调递减,则m的取值范围为
A. [-1,+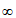 ) B. (-
) B. (-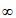 ,-1]
,-1]
C. [-2,+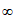 ) D. (-
) D. (-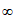 ,-2]
,-2]
8. 某四棱锥的三视图如图所示,该四棱锥中最长棱的棱长为
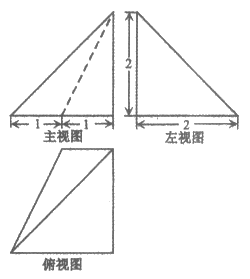
A. 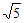 B. 2
B. 2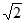
C. 2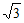 D.
D.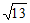
9. 若数列{an}满足a1=2,则”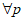 ,r
,r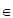 N*,
N*,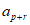 =
=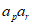 “是”{an}为等比数列”的
“是”{an}为等比数列”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
10. 形如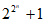 (n是非负整数)的数称为费马数,记为
(n是非负整数)的数称为费马数,记为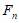 。数学家费马根据F0,F1,F2,F3,F4都是质数提出了猜想:费马数都是质数。多年之后,数学家欧拉计算出F5不是质数,那么F5的位数是
。数学家费马根据F0,F1,F2,F3,F4都是质数提出了猜想:费马数都是质数。多年之后,数学家欧拉计算出F5不是质数,那么F5的位数是
(参考数据:lg2≈0.3010)
A. 9 B. 10
C. 11 D. 12
第二部分 (非选择题 共110分)
二、填空题共5小题,每小题5分,共25分。
11. 已知点P(1,2)在抛物线C: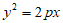 上,则抛物线C的准线方程为_______。
上,则抛物线C的准线方程为_______。
12. 在等差数列{an}中,a1=3,a2+ a5=16,则数列{an}的前4项的和为_______。
13. 已知非零向量a,b满足|a|=|a–b|,则(a–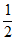 b)·b=_______。
b)·b=_______。
14. 在△ABC中,AB=4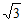 ,∠B=
,∠B=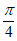 ,点D在边BC上,∠ADC=
,点D在边BC上,∠ADC=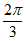 ,CD=2,则AD=_______;△ACD的面积为_______。
,CD=2,则AD=_______;△ACD的面积为_______。
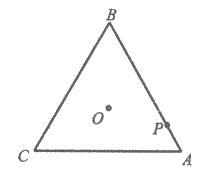
15. 如图,在等边三角形ABC中,AB=6。动点P从点A出发,沿着此三角形三边逆时针运动回到A点,记P运动的路程为x,点P到此三角形中心O距离的平方为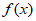 ,给出下列三个结论:
,给出下列三个结论:
①函数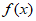 的最大值为12;
的最大值为12;
②函数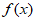 的图象的对称轴方程为x=9;
的图象的对称轴方程为x=9;
③关于x的方程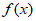 =kx+3最多有5个实数根。
=kx+3最多有5个实数根。
其中,所有正确结论的序号是_______。
注:本题给出的结论中,有多个符合题目要求。全部选对得5分,不选或有错选得0分,其他得3分。
三、解答题共6小题,共85分。解答应写出文字说明、演算步骤或证明过程。
16. (本小题共14分)
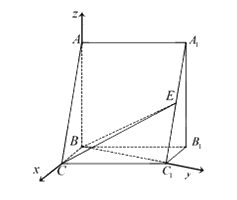
如图,在三棱柱ABC-A1B1C1中,AB⊥平面BB1C1C,AB=BB1=2BC=2,BC1=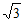 ,点E为A1C1的中点。
,点E为A1C1的中点。
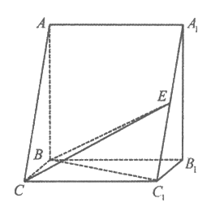
(I)求证:C1B⊥平面ABC;
(II)求二面角A-BC-E的大小。
17. (本小题共14分)
已知函数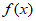 =2cos2
=2cos2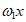 +sin
+sin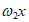 。
。
(I)求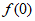 的值;
的值;
(II)从①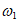 =1,
=1,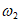 =2;②
=2;②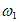 =1,
=1,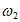 =l这两个条件中任选一个,作为题目的已知条件,求函数
=l这两个条件中任选一个,作为题目的已知条件,求函数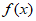 在[-
在[-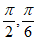 ]上的最小值,并直接写出函数
]上的最小值,并直接写出函数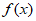 的一个周期。
的一个周期。
注:如果选择两个条件分别解答,按第一个解答计分。
18. (本小题共14分)
科技创新能力是决定综合国力和国际竞争力的关键因素,也是推动经济实现高质量发展的重要支撑,而研发投入是科技创新的基本保障。下图是某公司从2010年到2019年这10年研发投入的数据分布图:
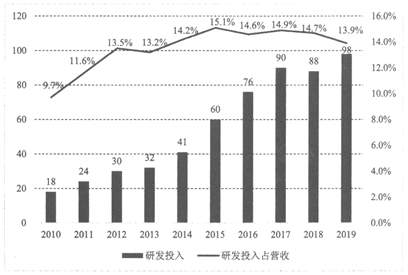
其中折线图是该公司研发投入占当年总营收的百分比,条形图是当年研发投入的数值(单位:十亿元)。
(I)从2010年至2019年中随机选取一年,求该年研发投入占当年总营收的百分比超过10%的概率;
(II)从2010年至2019年中随机选取两个年份,设X表示其中研发投入超过500亿元的年份的个数,求X的分布列和数学期望;
(III)根据图中的信息,结合统计学知识,判断该公司在发展的过程中是否比较重视研发,并说明理由。
19. (本小题共15分)
已知函数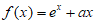 。
。
(I)当a=-1时,
①求曲线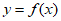 在点(0,
在点(0,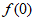 )处的切线方程;
)处的切线方程;
②求函数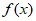 的最小值;
的最小值;
(II)求证:当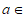 (-2,0)时,曲线
(-2,0)时,曲线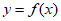 与
与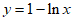 有且只有一个交点。
有且只有一个交点。
20. (本小题共14分)
己知椭圆C: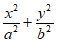 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为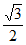 ,A1(-a,0),A2(a,0),B(0,b),△A1BA2的面积为2。
,A1(-a,0),A2(a,0),B(0,b),△A1BA2的面积为2。
(I)求椭圆C的方程;
(II)设M是椭圆C上一点,且不与顶点重合,若直线A1B与直线A2M交于点P,直线A1M与直线A2B交于点Q。求证:△BPQ为等腰三角形。
21. (本小题共14分)
已知数列{an}是由正整数组成的无穷数列。若存在常数k∈N*,使得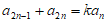 对任意的n
对任意的n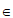 N*成立,则称数列{an}具有性质
N*成立,则称数列{an}具有性质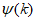 。
。
(I)分别判断下列数列{an}是否具有性质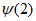 ;(直接写出结论)
;(直接写出结论)
①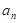 =1;②
=1;②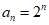 。
。
(II)若数列{an}满足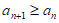 (n=l,2,3,…),求证:”数列{an}具有性质
(n=l,2,3,…),求证:”数列{an}具有性质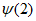 “是”数列{an}为常数列”的充分必要条件;
“是”数列{an}为常数列”的充分必要条件;
(III)已知数列{an}中a1=1,且an+1>an(n=l,2,3,…)。若数列{an}具有性质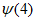 ,求数列{an}的通项公式。
,求数列{an}的通项公式。
参考答案
阅卷须知:
1. 评分参考中所注分数,表示考生正确做到此步应得的累加分数。
2. 其他正确解法可以参照评分标准按相应步骤给分。
一、选择题共10小题,每小题4分,共40分。
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | A | B | B | D | C | C | D | C | A | B |
二、填空题共5小题,每小题5分,共25分。
题号 | 11 | 12 | 13 | 14 | 15 |
答案 |
|
| 0 |
| ①② |
注:第14题第一空3分,第二空2分;第15题全部选对得5分,不选或有错选得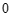 分,其他得3分。
分,其他得3分。
三、解答题共6小题,共85分。解答应写出文字说明、演算步骤或证明过程。
16. 解:(Ⅰ)因为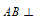 平面
平面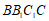 ,
,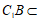 平面
平面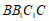
所以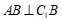 。
。
在△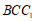 中,
中,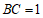 ,
,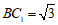 ,
,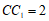 ,
,
所以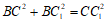 。
。
所以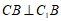 。
。
因为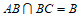 ,
, 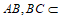 平面
平面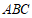 ,
,
所以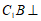 平面
平面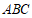 。
。
(Ⅱ)由(Ⅰ)知,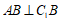 ,
,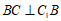 ,
,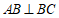 ,
,
如图,以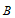 为原点建立空间直角坐标系
为原点建立空间直角坐标系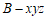 。
。
则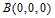 ,
,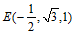 ,
,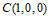 。
。
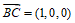 ,
,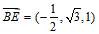 。
。
设平面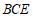 的法向量为
的法向量为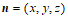 ,
,
则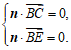
即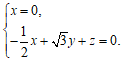
令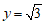 则
则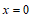 ,
,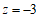 ,
,
所以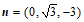 。
。
又因为平面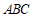 的法向量为
的法向量为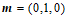 ,
,
所以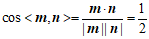 。
。
由题知二面角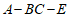 为锐角,所以其大小为
为锐角,所以其大小为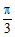 。
。
17. 解:(Ⅰ)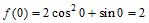 。
。
(Ⅱ)选择条件①。
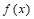 的一个周期为
的一个周期为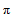 。
。
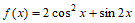
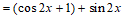
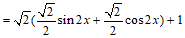
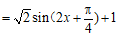 。
。
因为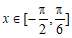 ,所以
,所以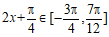 。
。
所以 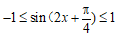 。
。
所以 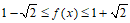 。
。
当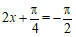 时,即
时,即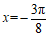 时,
时,
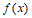 在
在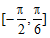 取得最小值
取得最小值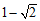 。
。
选择条件②。
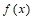 的一个周期为
的一个周期为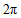 。
。
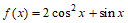
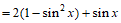
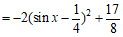 。
。
因为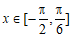 ,所以
,所以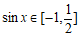 。
。
所以 当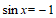 时,即
时,即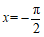 时,
时,
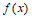 在
在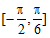 取得最小值
取得最小值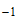 。
。
18. 解:(Ⅰ)设事件A为”从2010年至2019年中随机选取一年,研发投入占当年总营收的百分比超过10%”,从2010年至2019年一共10年,其中研发投入占当年总营收的百分比超过10%有9年,所以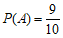 。
。
(Ⅱ)由图表信息,从2010年至2019年10年中有5年研发投入超过500亿元,所以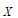 的所有可能取值为
的所有可能取值为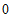 ,
,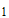 ,
,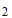 。
。
且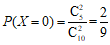 ;
;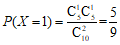 ;
;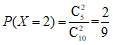 。
。
所以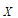 的分布列为:
的分布列为:
| 0 | 1 | 2 |
|
|
|
|
故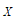 的期望
的期望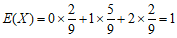 .
.
(Ⅲ)本题为开放问题,答案不唯一。 要求用数据说话,数据可以支持自己的结论即可,阅卷时按照上述标准酌情给分。
(19)解:(Ⅰ)①当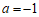 时,
时,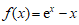 ,则
,则
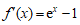 .
.
所以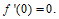
又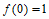 ,
,
所以曲线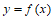 在点
在点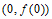 处的切线方程为
处的切线方程为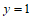
②令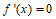 ,得
,得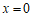 。
。
此时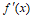 ,
,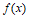 随
随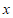 的变化如下:
的变化如下:
|
|
|
|
|
| 0 |
|
| ↘ | 极小值 | ↗ |
可知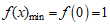 ,函数
,函数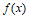 的最小值为1。
的最小值为1。
(Ⅱ)由题意可知,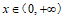 。
。
令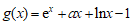 ,则
,则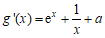 .
.
由(Ⅰ)中可知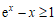 ,故
,故
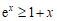 .
.
因为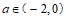 ,
,
则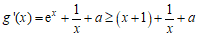
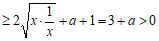 .
.
所以函数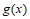 在区间
在区间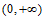 上单调递增。
上单调递增。
因为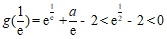 ,
,
又因为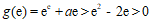 ,
,
所以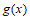 有唯一的一个零点。
有唯一的一个零点。
即函数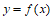 与
与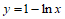 有且只有一个交点。
有且只有一个交点。
20. 解:(Ⅰ)由题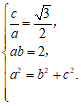
解得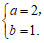
所以椭圆方程为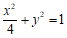 。
。
(II)解法1
证明:设直线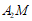 方程为
方程为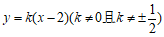 ,直线
,直线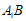 方程为
方程为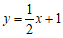
由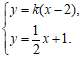 解得点
解得点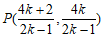 。
。
由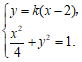 得
得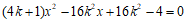 ,
,
则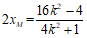 。
。
所以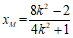 ,
,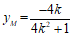 。
。
即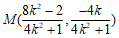 。
。
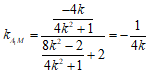 。
。
于是直线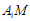 的方程为
的方程为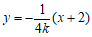 ,直线
,直线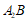 的方程为
的方程为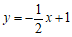 。
。
由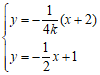 解得点
解得点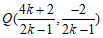
于是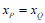 ,所以
,所以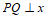 轴。
轴。
设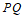 中点为
中点为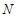 ,则
,则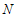 点的纵坐标为
点的纵坐标为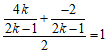 。
。
故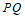 中点在定直线
中点在定直线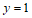 上。
上。
从上边可以看出点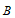 在
在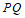 的垂直平分线上,所以
的垂直平分线上,所以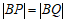 ,
,
所以△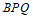 为等腰三角形。
为等腰三角形。
解法2
证明:设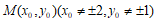 则
则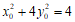 。
。
直线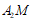 方程为
方程为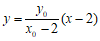 ,直线
,直线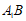 方程为
方程为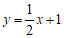 。
。
由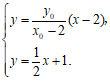
解得点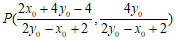 。
。
直线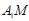 方程为
方程为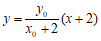 ,直线
,直线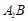 方程为
方程为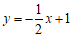 。
。
由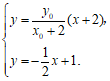
解得点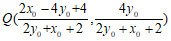 。
。
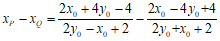
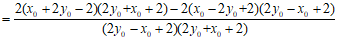
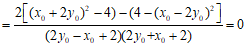 。
。
于是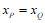 ,所以
,所以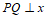 轴。
轴。
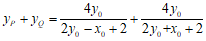
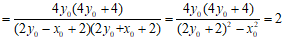 。
。
故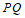 中点在定直线
中点在定直线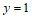 上。
上。
从上边可以看出点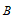 在
在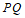 的垂直平分线上,所以
的垂直平分线上,所以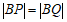 ,
,
所以△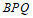 为等腰三角形。
为等腰三角形。
(21)解:(Ⅰ)①数列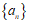 具有”性质
具有”性质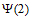 “;
“;
②数列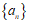 不具有”性质
不具有”性质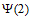 “。
“。
(Ⅱ)先证”充分性”:
当数列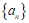 具有”性质
具有”性质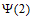 “时,有
“时,有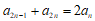
又因为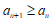 ,
,
所以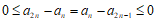 ,
,
进而有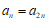
结合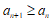 有
有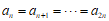 ,
,
即”数列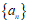 为常数列”;
为常数列”;
再证”必要性”:
若”数列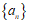 为常数列”,
为常数列”,
则有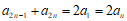 ,
,
即”数列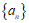 具有”性质
具有”性质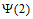 “。
“。
(Ⅲ)首先证明: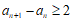 。
。
因为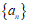 具有”性质
具有”性质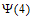 “,
“,
所以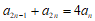 。
。
当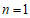 时有
时有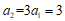 。
。
又因为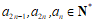 且
且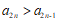 ,
,
所以有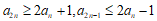 ,
,
进而有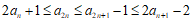 ,
,
所以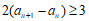 ,
,
结合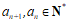 可得:
可得: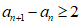 。
。
然后利用反证法证明: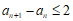 。
。
假设数列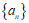 中存在相邻的两项之差大于2,
中存在相邻的两项之差大于2,
即存在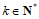 满足:
满足:
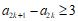 或
或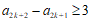 ,
,
进而有
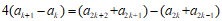
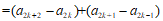
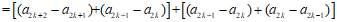
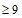 。
。
又因为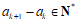 ,
,
所以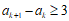
依次类推可得: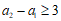 ,矛盾,
,矛盾,
所以有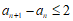 。
。
综上有: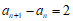 ,
,
结合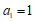 可得
可得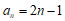 ,
,
经验证,该通项公式满足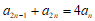 ,
,
所以: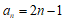 。
。