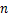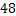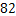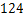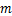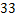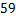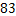本试卷共三道大题,28道小题。满分100分。考试时间120分钟。
一、选择题(本题共16分,每小题2分)
第1-8题均有四个选项,符合题意的选项只有一个.
1.下面的四个图形中,是圆柱的侧面展开图的是

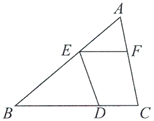
2.若代数式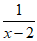 有意义,则实数
有意义,则实数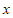 的取值范围是
的取值范围是
A. 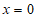 B.
B. 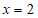 C.
C. 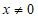 D.
D.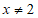
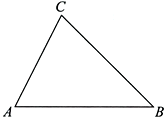
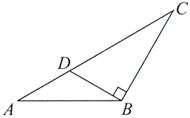
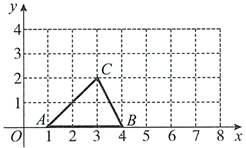
3.如图,在△ABC中,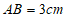 ,通过测量,并计算△ABC的面积,所得面积与下列数值最接近的是
,通过测量,并计算△ABC的面积,所得面积与下列数值最接近的是
A. 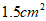 B.
B. 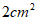 C.
C. 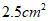 D.
D.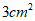
4.图中阴影部分是由4个完全相同的的正方形拼接而成,若要在①,②,③,④四个区域中的某个区域处添加一个同样的正方形,使它与阴影部分组成的新图形是中心对称图形,则这个正方形应该添加在
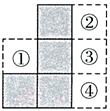
A. 区域①处 B. 区域②处 C. 区域③处 D. 区域④处
5.如图,在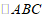 中,
中, 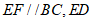 平分
平分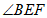 ,且
,且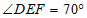 ,则
,则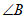 的度数为
的度数为
A.70° B.60° C.50° D.40°
6.如果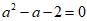 ,那么代数式
,那么代数式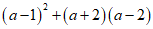 的值为
的值为
A.1 B.2 C.3 D.4
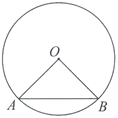
7.如图, 的半径等于4,如果弦
的半径等于4,如果弦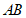 所对的圆心角等于
所对的圆心角等于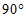 ,那么圆心
,那么圆心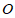 到弦
到弦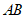 的距离为
的距离为
A.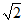 B.
B.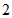 C.
C.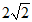 D.
D.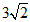
8.在平面直角坐标系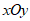 中,对于点
中,对于点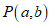 ,若
,若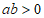 ,则称点
,则称点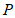 为”同号点”.下列函数的图象中不存在”同号点”的是
为”同号点”.下列函数的图象中不存在”同号点”的是
A.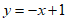 B.
B.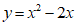 C.
C.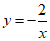 D.
D.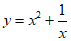
二、填空题(本题共16分,每小题2分)
9.单项式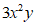 的系数是
的系数是
.
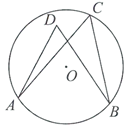
10.如图,点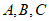 在
在 上,点
上,点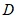 在
在 内,则
内,则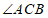
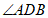 .(填
.(填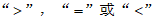 )
)
11.下表记录了一名篮球运动员在罚球线上投篮的结果:
投篮次数 |
|
|
|
|
|
|
|
投中次数 |
|
|
|
|
|
|
|
投中频率 |
|
|
|
|
|
|
|
根据上表,这名篮球运动员投篮一次,投中的概率约为
.(结果精确到0.01)
12.函数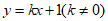 的图象上有两点
的图象上有两点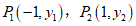 ,若
,若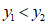 ,写出一个符合题意的
,写出一个符合题意的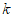 的值:
的值:
.
13.如图,在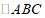 中,
中,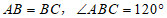 ,过点
,过点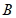 作
作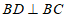 ,交
,交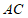 于点
于点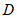 ,若
,若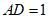 ,则
,则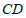 的长度为
的长度为
.
14.如图,在平面直角坐标系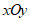 中,已知点
中,已知点 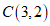 ,将
,将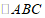 关于直线
关于直线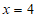 对称,得到
对称,得到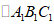 ,则点
,则点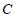 的对应点
的对应点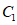 的坐标为
的坐标为
;再将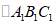 向上平移一个单位长度,得到
向上平移一个单位长度,得到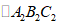 ,则点
,则点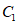 的对应点
的对应点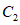 的坐标为
的坐标为
.
15.小华和小明周末到北京三山五园绿道骑行.他们按设计好的同一条线路同时出发,小华每小时骑行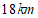 ,小明每小时骑行
,小明每小时骑行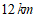 ,他们完成全部行程所用的时间,小明比小华多半小时.设他们这次骑行线路长为
,他们完成全部行程所用的时间,小明比小华多半小时.设他们这次骑行线路长为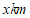 ,依题意,可列方程为
,依题意,可列方程为
.
16.如图,在平面直角坐标系 中,有五个点
中,有五个点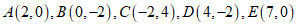 ,将二次函数
,将二次函数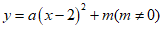 的图象记为
的图象记为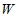 .下列的判断中
.下列的判断中
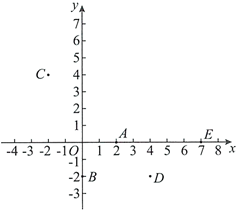
①点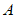 一定不在
一定不在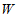 上;
上;
②点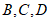 可以同时在
可以同时在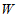 上;
上;
③点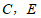 不可能同时在
不可能同时在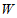 上.
上.
所有正确结论的序号是
.
三、解答题(本题共68分,第17~22题,每小题5分,第23~26题,每小题6分,第27~28题,每小题7分)解答应写出文字说明、演算步骤或证明过程.
17.计算: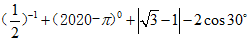
18.解不等式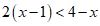 ,并在数轴上表示出它的解集.
,并在数轴上表示出它的解集.
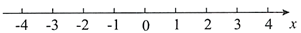
19.下面是小王同学”过直线外一点作该直线的平行线”的尺规作图过程.
已知:直线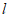 及直线
及直线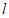 外一点
外一点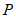 .
.
求作:直线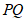 ,使得
,使得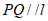 .
.

作法:如图,
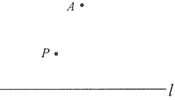
①在直线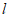 外取一点
外取一点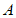 ,作射线
,作射线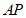 与直线
与直线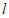 交于点
交于点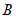 ,
,
②以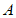 为圆心,
为圆心,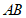 为半径画弧与直线
为半径画弧与直线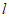 交于点
交于点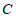 ,连接
,连接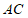 ,
,
③以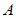 为圆心,
为圆心,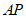 为半径画弧与线段
为半径画弧与线段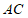 交于点
交于点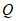 ,
,
则直线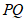 即为所求.
即为所求.
根据小王设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明: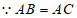 ,
,
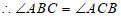 ,(
,(
)(填推理的依据)
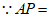 ______________,
______________,
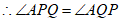 .
.
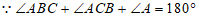 ,
,
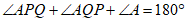 ,
,
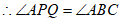 .
.
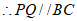 (
(
)(填推理的依据).
即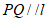 .
.
20.已知关于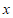 的一元二次方程
的一元二次方程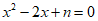 .
.
(1)如果此方程有两个相等的实数根,求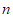 的值;
的值;
(2)如果此方程有一个实数根为0,求另外一个实数根.
21.如图,在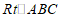 中,
中,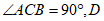 为
为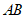 边的中点,连接
边的中点,连接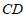 ,过点
,过点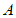 作
作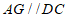 ,过点
,过点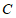 作
作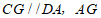 与
与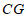 相交于点
相交于点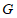
(1)求证:四边形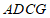 是菱形;
是菱形;
(2)若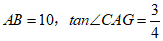 ,求
,求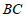 的长.
的长.
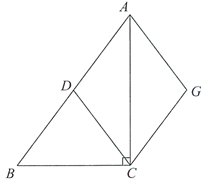
22.坚持节约资源和保护环境是我国的基本国策,国家要求加强生活垃圾分类回收与再生资源回收有效衔接,提高全社会资源产出率,构建全社会的资源循环利用体系.图1反映了2014-2019年我国生活垃圾清运量的情况.
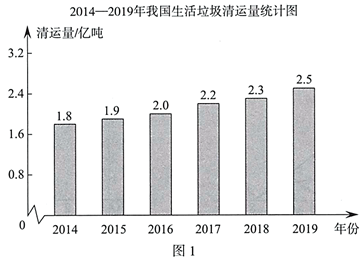
图2反映了2019年我国G市生活垃圾分类的情况.
根据以上材料回答下列问题:
(1)图2中,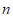 的值为
的值为
;
(2)2014-2019年,我国生活垃圾清运量的中位数是
;
(3)据统计,2019年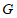 市清运的生活垃圾中可回收垃圾约为0.02亿吨,所创造的经济总价值约为40亿元.若2019年我国生活垃圾清运量中,可回收垃圾的占比与
市清运的生活垃圾中可回收垃圾约为0.02亿吨,所创造的经济总价值约为40亿元.若2019年我国生活垃圾清运量中,可回收垃圾的占比与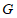 市的占比相同,根据
市的占比相同,根据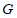 市的数据估计2019年我国可回收垃圾所创造的经济总价值是多少.
市的数据估计2019年我国可回收垃圾所创造的经济总价值是多少.
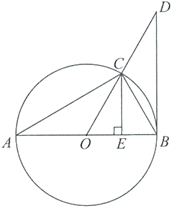
23.如图,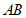 为
为 的直径,
的直径,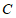 为
为 上一点,
上一点,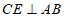 于点
于点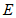 ,
, 的切线
的切线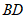 交
交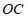 的延长线于点
的延长线于点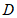 .
.
(1)求证: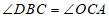 ;
;
(2)若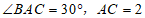 .求
.求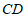 的长.
的长.
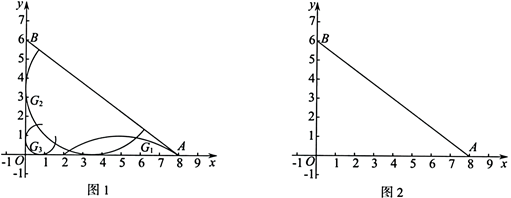
24.如图,在平面直角坐标系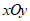 中,函数
中,函数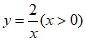 的图象与直线
的图象与直线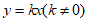 交于点
交于点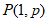 .
.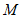 是函数
是函数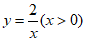 图象上一点,过
图象上一点,过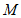 作
作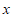 轴的平行线交直线
轴的平行线交直线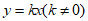 于点
于点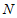 .
.
(1)求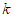 和
和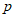 的值;
的值;
(2)设点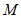 的横坐标为
的横坐标为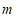 .
.
①求点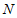 的坐标;(用含
的坐标;(用含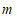 的代数式表示)
的代数式表示)
②若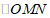 的面积大于
的面积大于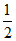 ,结合图象直接写出
,结合图象直接写出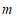 的取值范围.
的取值范围.
25.如图1,在四边形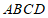 中,对角线
中,对角线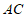 平分
平分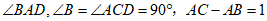 .为了研究图中线段之间的数量关系,设
.为了研究图中线段之间的数量关系,设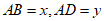 .
.
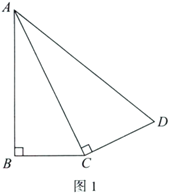
(1)由题意可得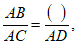 (在括号内填入图1中相应的线段)
(在括号内填入图1中相应的线段)
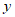 关于
关于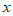 的函数表达式为
的函数表达式为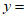
;
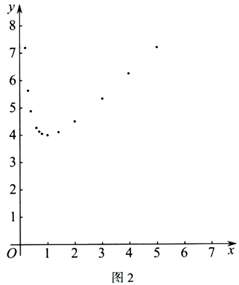
(2)如图2,在平面直角坐标系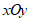 中,根据(1)中
中,根据(1)中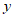 关于
关于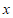 的函数表达式描出了其图象上的一部分点,请依据描出的点画出该函数的图象;
的函数表达式描出了其图象上的一部分点,请依据描出的点画出该函数的图象;
(3)结合函数图象,解决问题:①写出该函数的一条性质:
;
②估计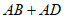 的最小值为
的最小值为
.(结果精确到0.1)
26.在平面直角坐标系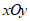 中,已知二次函数
中,已知二次函数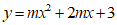 的图象与
的图象与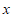 轴交于点
轴交于点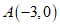 ,与
,与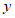 轴交于点
轴交于点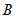 ,将其图象在点
,将其图象在点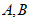 之间的部分(含
之间的部分(含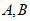 两点)记为
两点)记为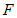 .
.
(1)求点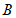 的坐标及该函数的表达式;
的坐标及该函数的表达式;
(2)若二次函数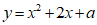 的图象与
的图象与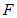 只有一个公共点,结合函数图象,求
只有一个公共点,结合函数图象,求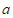 的取值范围.
的取值范围.
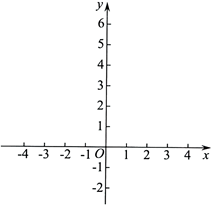
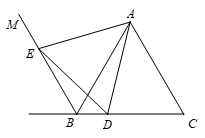
27.如图1,等边三角形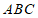 中,
中,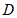 为
为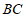 边上一点,满足
边上一点,满足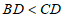 ,连接
,连接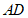 ,以点
,以点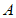 为中心将射线
为中心将射线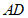 顺时针旋转
顺时针旋转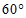 ,与
,与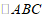 的外角平分线
的外角平分线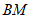 交于点
交于点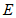 .
.
(1)依题意补全图1;
(2)求证: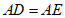 ;
;
(3)若点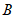 关于直线
关于直线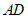 的对称点为
的对称点为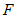 ,连接
,连接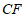 .
.
①求证: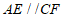 ;
;
②若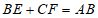 成立,直接写出
成立,直接写出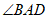 的度数为
的度数为
°
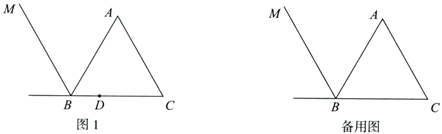
28.在平面内,对于给定的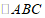 ,如果存在一个半圆或优弧与
,如果存在一个半圆或优弧与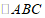 的两边相切,且该弧上的所有点都在
的两边相切,且该弧上的所有点都在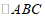 的内部或边上,则称这样的弧为
的内部或边上,则称这样的弧为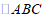 的内切弧.当内切弧的半径最大时,称该内切弧为
的内切弧.当内切弧的半径最大时,称该内切弧为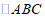 的完美内切弧.(注:弧的半径指该弧所在圆的半径)在平面直角坐标系
的完美内切弧.(注:弧的半径指该弧所在圆的半径)在平面直角坐标系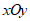 中,
中,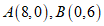 .
.
(1)如图1,在弧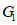 ,弧
,弧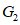 ,弧
,弧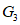 中,是
中,是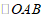 的内切弧的是
的内切弧的是
;
(2)如图2,若弧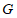 为
为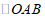 的内切弧,且弧
的内切弧,且弧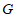 与边
与边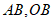 相切,求弧
相切,求弧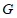 的半径的最大值;
的半径的最大值;
(3)如图3,动点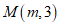 ,连接
,连接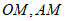 .
.
①直接写出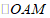 的完美内切弧的半径的最大值;
的完美内切弧的半径的最大值;
②记①中得到的半径最大时的完美内切弧为弧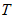 .点
.点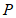 为弧
为弧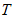 上的一个动点,过点
上的一个动点,过点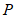 作
作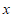 轴的垂线,分别交
轴的垂线,分别交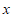 轴和直线
轴和直线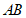 于点
于点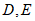 ,点
,点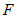 为线段
为线段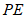 的中点,直接写出线段
的中点,直接写出线段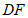 长度的取值范围.
长度的取值范围.
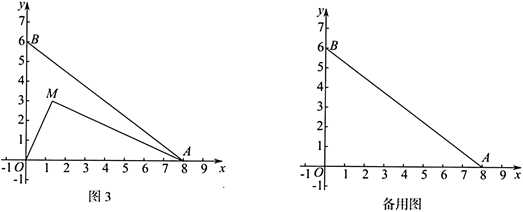
【试题答案】
一、选择题
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | A | D | D | B | D | A | C | C |
二、填空题
9. 3 10. < 11. 0.68 12. 1 (答案不唯一)
13. 2 14. (5,2),(5,3) 15. 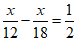 16. ①②
16. ①②
注:第14题每空1分;第16题答对一个得1分,答对2个得满分,含有错误答案得0分
三、解答题
17.解:原式=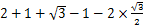
=2
18.解:去括号,得:
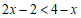 .
.
移项,得: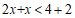 .
.
合并同类项,得: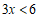 .
.
系数化成1得: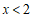 .
.
该不等式的解集在数轴上表示为:

19.解:(1)补全图形如图所示:
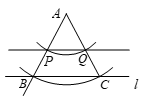
(2)等边对等角.
AQ.
同位角相等,两直线平行.
20.解:(1)∵原方程有两个相等实数根,
∴Δ=0.
即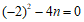 .
.
∴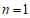 .
.
(2)∵原方程有一个实数根为0,
∴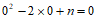
即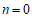 .
.
∴原方程可化为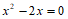 .
.
∴另一个根为2.
21.(1)证明:
∵AG∥DC,CG∥DA,
∴四边形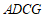 为平行四边形.
为平行四边形.
∵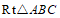 中,
中,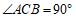 ,
,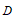 为
为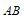 边的中点,
边的中点,
∴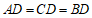 .
.
∴四边形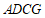 是菱形.
是菱形.
(2)解:∵四边形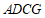 是菱形,
是菱形,
∴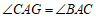 .
.
∵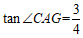 ,
,
∴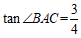 .
.
∴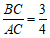 .
.
∵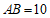 ,
,
∴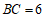 .
.
22.解:(1)18.
(2)2.1.
(3)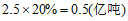
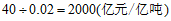
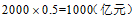
答:根据G市的数据估计2019年我国可回收垃圾所创造的经济总价值是1000亿元.
23.(1)证明:
∵DB是⊙O的切线,
∴∠OBD=∠OBC+∠DBC=90°.
∵AB是⊙O的直径,
∴∠ACB=∠OCA+∠OCB=90°.
∵OC=OB,
∴∠OBC=∠OCB.
∴∠DBC=∠OCA.
(2)解:在Rt△ACB中,∠A=30°,AC=2,可得CB=ACtanA=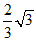 .
.
∵∠A=30°,
∴∠COB=2∠A=60°.
∴∠D=90°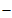 ∠COB=30°.
∠COB=30°.
∵OA=OC,
∴∠OCA=∠A=30°.
∴∠DBC=∠OCA=30°.
∴∠D=∠DBC.
∴CB=CD.
∴CD=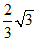 .
.
24.解:(1)依题意,P(1,p)在函数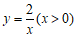 的图象上,
的图象上,
可得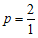 =2,得点P(1,2).
=2,得点P(1,2).
将P(1,2)代入直线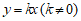 ,得
,得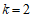 .
.
(2)①由于M是函数 图象上一点,且点M的横坐标为m,
图象上一点,且点M的横坐标为m,
可得点M的纵坐标为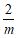 .
.
又因为过M作x轴的平行线交直线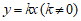 于点N,
于点N,
得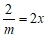 ,解得
,解得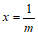 ,即N点坐标为(
,即N点坐标为(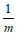 ,
,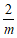 ).
).
②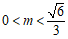 或者
或者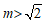 .
.
25.解:(1)AC,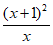 .
.
(2)如图所示:
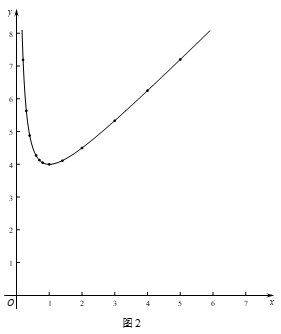
(3)①当x>1时,y随x的增大而增大(答案不唯一).
②4.8.
26.解:(1)∵y=mx2+2mx+3的图象与与y轴交于点B,
∴点B的坐标为(0,3).
∵y=mx2+2mx+3的图象与x轴交于点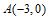 ,
,
∴将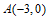 代入y=mx2+2mx+3可得
代入y=mx2+2mx+3可得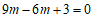 .
.
∴m=-1.
∴该函数的表达式为y=-x2-2x+3.
(2)∵将二次函数y=mx2+2mx+3的图象在点A,B之间的
部分(含A,B两点)记为F,
∴F的端点为A,B,并经过抛物线y=mx2+2mx+3的
顶点C(其中C点坐标为(-1,4)).
∴可画F如图1所示.
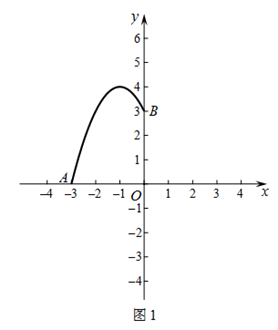
∵二次函数y=x2+2x+a的图象的对称轴为x=-1,
且与F只有一个公共点,
∴可分别把A,B,C的坐标代入解析式y=x2+2x+a中.
∴可得三个a值分别为-3,3,5.
可画示意图如图2所示.
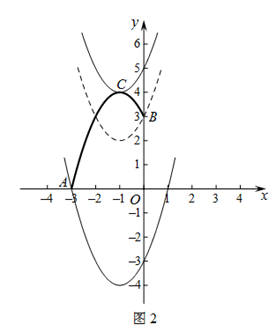
∴结合函数图象可知:
二次函数y=x2+2x+a的图象与F只有一个公共点时,
a的取值范围是-3≤a<3或a=5.
27.(1)依题意补全图形
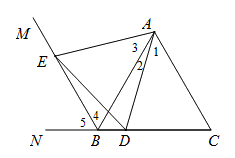
(2)证明:
∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠ABC=∠C=60°.
∴∠1+∠2=60°.
∵射线AD绕点A顺时针旋转60°得到射线AE,
∴∠DAE=60°.
∴∠2+∠3=60°.
∴∠1=∠3.
∵∠ABC=60°,
∴∠ABN=180°-∠ABC=120°.
∵BM平分∠ABN,
∴∠4=∠5=60°.
∴∠4=∠C.
∴△ABE≌△ACD.
∴AD=AE.
(3)①证明:连接AF,设∠BAD=α,
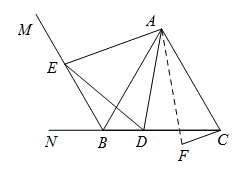
∵点B与点F关于直线AD对称,
∴∠FAD=∠BAD=α,FA=AB.
∵∠DAE=60°,
∴∠BAE=∠DAE-∠DAB=60°-α.
∵等边三角形ABC中,∠BAC=60°,
∴∠EAC=∠BAE+∠BAC=120°-α.
∵AB=AC,AF=AB,
∴AF=AC.
∴∠F=∠ACF.
∵∠FAC=∠BAC-∠FAD-∠BAD=60°-2α,
且∠F+∠ACF+∠FAC=180°,
∴∠ACF=60°+α.
∴∠EAC+∠ACF=180°.
∴AE∥CF.
②20°.
28.解:(1)弧G2,弧G3.
(2)∵弧G为△OAB的内切弧,且弧G与边AB,OB相切,
∴弧G所在圆的圆心在∠OBA的角平分线BI上.
易知若弧G的半径最大,则弧G所在圆的圆心I在△OAB的边OA上.设弧G与边AB,OB相切分别切于点O,H.
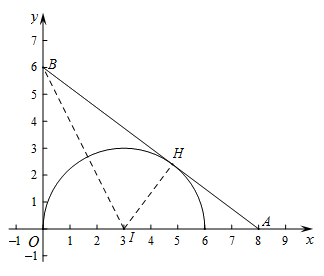
∴IH⊥AB.
∵A(8,0),B(0,6),
∴BO=6,AO=8,AB=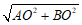 =10.
=10.
∵∠IOB=∠IHB=90°,OI=IH,BI=BI,
∴△IOB≌△IHB.
∴BH=BO=6.
∴AH=AB-BH=4,AI=AO-OI=8-OI,OI=HI.
在Rt△AIH中,AI2=AH2+HI2,即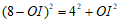 .
.
解得OI=3.
(3)①△OAM的完美内切弧半径的最大值为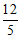 .
.
②线段DF长度的取值范围是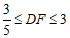 且
且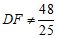 .
.
注:本试卷各题中若有其他合理的解法请酌情给分.