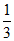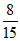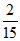本试卷满分共150分 考试时间120分钟
第一部分(选择题 共40分)
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 集合A={x∈Z|-2<x<2)的子集个数为
(A)4 (B)6 (C)7 (D)8
2. 函数 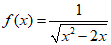 的定义域为
的定义域为
(A)(0,2) (B)[0,2]
(C)(-∞,0) 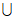 (2,+∞) (D)(-∞,0]
(2,+∞) (D)(-∞,0] 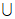 [2,+∞)
[2,+∞)
3. 下列函数中,最小正周期为π的是
(A) 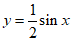 (B)
(B)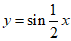
(C) 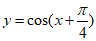 (D)
(D)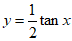
4. 已知数列{an}的前n项和Sn=n2-n,则a2+a3=
(A)3 (B)6 (C)7 (D)8
5. 设a,b为非零向量,则”a⊥b”是”|a+b|=|a-b|”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
6. 已知抛物线M:x2=2py(p>0)的焦点与双曲线N: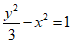 的一个焦点重合,则p=
的一个焦点重合,则p=
(A) 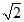 (B)2 (C)
(B)2 (C) 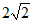 (D)4
(D)4
7. 已知函数f(x)=ln(1-x)- ln(1+x),则f(x)
(A)是奇函数,且在定义域上是增函数
(B)是奇函数,且在定义域上是减函数
(C)是偶函数,且在区间(0,1)上是增函数
(D)是偶函数,且在区间(0,1)上是减函数
8. 如图所示,一个三棱锥的主视图和左视图均为等边三角形,俯视图为等腰直角三角形,则该棱锥的体积为
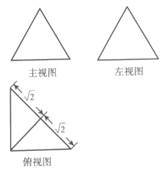
(A) 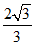 (B)
(B)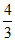
(C) 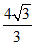 (D)
(D)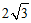
9. 在△ABC中,AC=3,BC=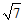 ,AB=2,则AB边上的高等于
,AB=2,则AB边上的高等于
(A) 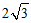 (B)
(B) 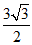 (C)
(C) 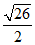 (D)
(D)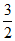
10.某中学举行了科学防疫知识竞赛。经过选拔,甲、乙、丙三位选手进入了的最后角逐。他们还将进行四场知识竞赛。规定:每场知识竞赛前三名的得分依次为a,b,c(a>b>c,且a,b,c∈N*);选手总分为各场得分之和。四场比赛后,已知甲最后得分为16分,乙和丙最后得分都为8分,且乙只有一场比赛获得了第一名,则下列说法正确的是
(A)每场比赛的第一名得分a为4 (B)甲至少有一场比赛获得第二名
(C)乙在四场比赛中没有获得过第二名 (D)丙至少有一场比赛获得第三名
第二部分(非选择题 共110分)
二、填空题共5小题,每小题5分,共25分。
11. 已知复数z=2-i,则|z|=______________.
12. 已知直线x+y+1=0的倾斜角为α,则cosα=____________.
13. 双曲线M: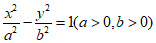 的离心率为
的离心率为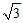 ,则其渐近线方程为_________。
,则其渐近线方程为_________。
14. 天干地支纪年法(简称干支纪年法)是中国历法上自古以来就一直使用的纪年方法。天干有十,即:甲、乙、丙、丁、戊、己、庚、辛、壬、癸;地支有十二,即:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥。干支纪年法天干地支对应的规律如下表:
天干 | 甲 | 乙 | 丙 | 丁 | 戊 | 己 | 庚 | 辛 | 壬 | 癸 | 甲 | 乙 | 丙 | … |
地支 | 子 | 丑 | 寅 | 卯 | 辰 | 巳 | 午 | 未 | 申 | 酉 | 戌 | 亥 | 子 | … |
干支 纪年 | 甲 子 年 | 乙 丑 年 | 丙 寅 年 | 丁 卯 年 | 戊 辰 年 | 己 巳 年 | 庚 午 年 | 辛 未 年 | 壬 申 年 | 癸 酉 年 | 甲 戌 年 | 乙 亥 年 | 丙 子 年 | … |
2049年是新中国成立100周年。这一百年,中国逐步实现中华民族的伟大复兴。使用干支纪年法,2049年是己巳年,则2059年是_________年;使用于支纪年法可以得到________种不同的干支纪年。
15. 已知集合P={(x,y){(x-cosθ)2+(y-sinθ)2=4,0≤θ≤π}。由集合P中所有的点组成的图形如图中阴影部分所示,中间白色部分形如美丽的”水滴”。给出下列结论:
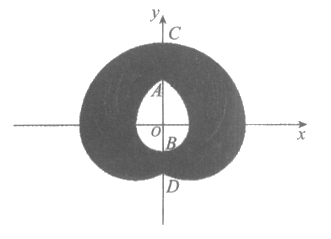
①”水滴”图形与y轴相交,最高点记为A,则点A的坐标为(0,1);
②在集合P中任取一点M,则M到原点的距离的最大值为3;
③阴影部分与y轴相交,最高点和最低点分别记为C,D,则|CD|=3+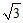 ;
;
④白色”水滴”图形的面积是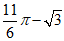 .
.
其中正确的有_________。
注:本题给出的结论中,有多个符合题目要求。全部选对得5分,不选或有错选得0分,其他得3分。
三、解答题共6小题,共85分,解答应写出文字说明,演算步骤或证明过程。
16. (本小题共14分)
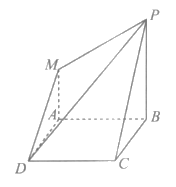
如图,四边形ABCD为正方形,MA∥PB,MA⊥BC,AB⊥PB,MA=1,AB=PB=2。
(I)求证:PB⊥平面ABCD;
(Ⅱ)求直线PC与平面PDM所成角的正弦值。
17. (本小题共14分)
已知等差数列{an}的前n项和为Sn,a1=2,S5=20。
(I)求数列{an}的通项公式;
(Ⅱ)若等比数列{bn}满足a4+b4=9,且公比为q,从①q=2;②q=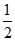 ;③q=-1
;③q=-1
这三个条件中任选一个作为题目的已知条件,求数列{an-bn}的前n项和Tn。
注:如果选择多个条件分别解答,按第一个解答计分。
18. (本小题共14分)
为了增强学生的冬奥会知识,弘扬奥林匹克精神,北京市多所中小学校开展了模拟冬奥会各项比赛的活动,为了了解学生在越野滑轮和旱地冰壶两项中的参与情况,在北京市中小学学校中随机抽取了10所学校,10所学校的参与人数如下:
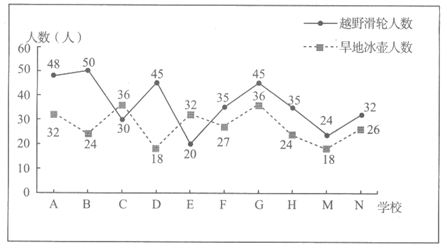
(I)现从这10所学校中随机选取2所学校进行调查,求选出的2所学校参与越野滑轮人数都超过40人的概率;
(II)现有一名旱地冰壶教练在这10所学校中随机选取2所学校进行指导,记X为教练选中参加旱地冰壶人数在30人以上的学校个数,求X的分布列和数学期望;
(Ⅲ)某校聘请了一名越野滑轮教练,对高山滑降、转弯、八字登坡滑行这3个动作进行技术指导。规定:这3个动作中至少有2个动作达到”优”,总考核记为”优”,在指导前,该校甲同学3个动作中每个动作达到”优”的概率均为0.1。在指导后的考核中,甲同学总考核成绩为”优”。能否认为甲同学在指导后总考核达到”优”的概率发生了变化?请说明理由。
19. (本小题共15分)
已知函数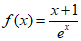 。
。
(I)求函数f(x)的极值;
(Ⅱ)求证:当x∈(0,+∞)时, 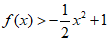 ;
;
(Ⅲ)当x>0时,若曲线y=f(x)在曲线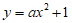 的上方,求实数a的取值范围。
的上方,求实数a的取值范围。
20. (本小题共14分)
已知椭圆C: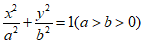 经过A(1,0),B(0,b)两点。O为坐标原点,且△AOB的面积为
经过A(1,0),B(0,b)两点。O为坐标原点,且△AOB的面积为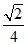 。过点P(0,1)且斜率为k(k>0)的直线l与椭圆C有两个不同的交点M,N,且直线AM,AN分别与y轴交于点S,T.
。过点P(0,1)且斜率为k(k>0)的直线l与椭圆C有两个不同的交点M,N,且直线AM,AN分别与y轴交于点S,T.
(I)求椭圆C的方程;
(Ⅱ)求直线l的斜率k的取值范围;
(Ⅲ)设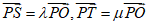 ,求λ+μ的取值范围。
,求λ+μ的取值范围。
21.(本小题共14分)
已知无穷集合A,B,且A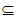 N,B
N,B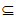 N,记A+B={a+b|a∈A,b∈B},定义:满足N*
N,记A+B={a+b|a∈A,b∈B},定义:满足N*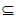 (A+B)时,则称集合A,B互为”完美加法补集”。
(A+B)时,则称集合A,B互为”完美加法补集”。
(I)已知集合A={a|a=2m+1,m∈N),B={b|b=2n,n∈N)。判断2019和2020是否属于集合A+B,并说明理由;
(Ⅱ)设集合
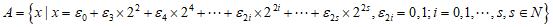
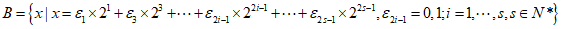 (i)求证:集合A,B互为”完美加法补集”;
(i)求证:集合A,B互为”完美加法补集”;
(ii)记A(n)和B(n)分别表示集合A,B中不大于n(n∈N*)的元素个数,写出满足A(n)B(n)=n+1的元素n的集合。(只需写出结果,不需要证明)
参考答案
一、选择题共10小题,每小题4分,共40分。
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | D | C | D | B | C | D | B | A | B | C |
二、填空题共5小题,每小题5分,共25分。
11. 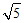 12.
12. 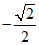 13.
13.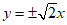
14. 己卯;60 15. ②③④
三、解答题共6小题,共85分。解答应写出文字说明,演算步骤或证明过程。
16. (本小题共14分)
证明:(I)因为MA⊥BC,MA∥PB,
所以PB⊥BC,
因为AB⊥PB,AB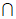 BC=B,
BC=B,
所以PB⊥平面ABCD。 ……5分
(II)因为PB⊥平面ABCD,
AB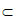 平面ABCD,AD
平面ABCD,AD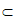 平面ABCD,
平面ABCD,
所以PB⊥AB,PB⊥AD。
因为四边形ABCD为正方形,
所以AB⊥BC。
如图建立空间直角坐标系B-xyz,
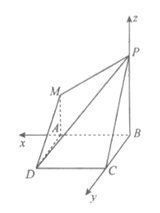
则P(0,0,2),M(2,0,1),C(0,2,0),D(2,2,0),
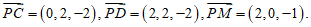
设平面PDM的法向量为u=(x,y,z),
则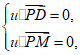 即
即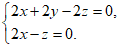
令z=2,则x=1,y=-1。于是u=(1,1,2)。
平面PDM的法向量为u=(1,1,2)。
设直线PC与平面PDM所成的角为θ,
所以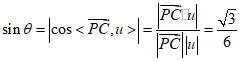 .
.
所以直线PC与平面PDM所成角的正弦值为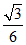 .………14分
.………14分
17. (本小题共14分)
解: (I)设等差数列{an}的公差为d,
又因为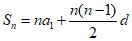 ,且a1=2,
,且a1=2,
所以S5=10+10d=20,故d=1.
所以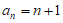 。 ……6分
。 ……6分
(II)由(I)可知,a4=5,又a4 +b4=9,所以b4 =4.
若选择条件①q=2,可得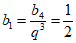 ,
,
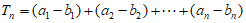
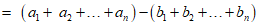
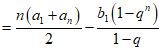
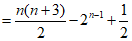 。 ………14分
。 ………14分
若选择条件②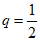 ,可得
,可得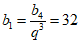 ,
,
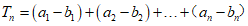
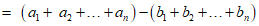
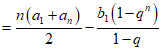
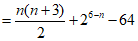
若选择条件③q=-1,可得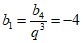 ,
,
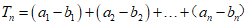
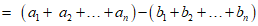
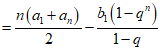
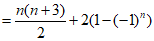 .
.
18. (本小题共14分)
解:(I)记”选出的两所学校参与越野滑轮人数都超过40人”为事件S,
参与越野滑轮人数超过40人的学校共4所,随机选择2所学校共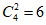 种,
种,
所以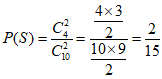 ………4分
………4分
(II) X的所有可能取值为0,1,2,参加旱地冰壶人数在30人以上的学校共4所,
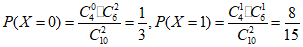 ,
,
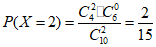
X的分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
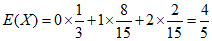 ………11分
………11分
(III)答案不唯一。
答案示例1:可以认为甲同学在指导后总考核为”优”的概率发生了变化。理由如下:
指导前,甲同学总考核为”优”的概率为:
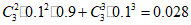
指导前,甲同学总考核为”优”的概率非常小,一旦发生,就有理由认为指导后总考核达到”优”的概率发生了变化。
答案示例2:无法确定。理由如下:
指导前,甲同学总考核为”优”的概率为:
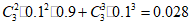
虽然概率非常小,但是也可能发生,
所以,无法确定总考核达到”优”的概率发生了变化。 ……14分
19. (本小题共15分)
解:(I)因为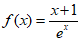 ,定义域R,
,定义域R,
所以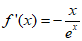 .
.
令f'(x)=0,解得x=0。
随x的变化,f'(x)和f(x)的情况如下:
x | (-∞,0) | 0 | (0,+∞) |
f’(x) | + | 0 | – – |
f(x) | ↗ | 极大值 | ↘ |
由表可知函数f(x)在x=0时取得极大值f(0)=1,无极小值。 ………5分
(II)令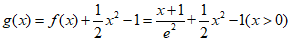 ,
,
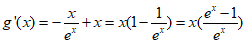
由x>0得ex -1>0,
于是g'(x)>0,
故函数g(x)是[0,+∞)上的增函数。
所以当x∈(0,+∞)时,g(x)>g(0)=0,即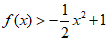 。 ………9分
。 ………9分
(III)当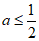 时,由(II)知
时,由(II)知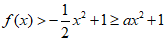 ,满足题意。
,满足题意。
令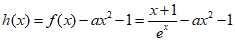
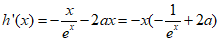
当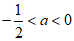 时,若x∈
时,若x∈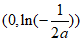 ,
, ,
,
则h(x)在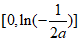 上是减函数。
上是减函数。
所以x∈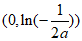 时,h(x)<h(0)=0,不合题意。
时,h(x)<h(0)=0,不合题意。
当a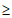 0时h'(x)<0,则h(x)在(0,+∞)上是减函数,
0时h'(x)<0,则h(x)在(0,+∞)上是减函数,
所以h(x)<h(0)=0,不合题意,
综上所述,实数a的取值范围 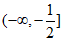 。 ……15分
。 ……15分
20.(本小题共14分)
解:(I)因为椭圆C: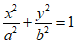 经过点A(1,0),
经过点A(1,0),
所以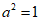 解得a=1.
解得a=1.
由△AOB的面积为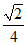 可知,
可知,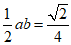 ,
,
解得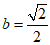 ,
,
所以椭圆C的方程为x2+2y2=1。 ……………………3分
(II)设直线l的方程为y=kx+1,M(x1,y1),N(x2,y2)。
联立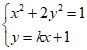 ,消y整理可得:
,消y整理可得: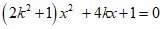 。
。
因为直线与椭圆有两个不同的交点,
所以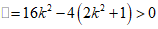 ,解得
,解得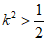 。
。
因为k>0,所以k的取值范围是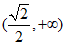 。 ………7分
。 ………7分
(III)因为A(1,0),P(0,1)M(x1,y1),N(x2, y2),
所以直线AM的方程是: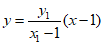 。
。
令x=0,解得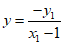
所以点S的坐标为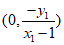 。
。
同理可得:点T的坐标为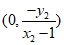 。
。
所以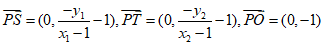 .
.
由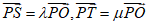 ,
,
可得: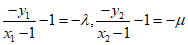
所以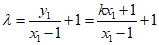 .
.
同理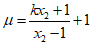
由(II)得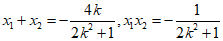
所以
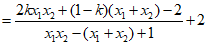
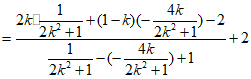
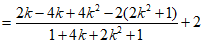
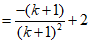
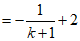
所以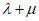 的范围是
的范围是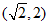 。 …14分
。 …14分
21. (本小题共14分)
解:(I)由a=2m+1,b=2n得a+b= 2(m+n)+1是奇数,
当a= 2×1009+1,b=2×0=0时,a+b= 2019,
所以2019∈A+B,2020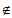 A+B. ……………4分
A+B. ……………4分
(II)(i)首先证明:对于任意自然数p可表示为唯一一数组(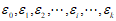 ),
),
其中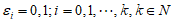
使得
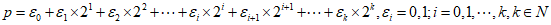 由于
由于
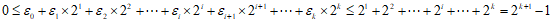 这种形式的自然数p至多有
这种形式的自然数p至多有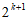 个,且最大数不超过
个,且最大数不超过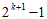 。
。
由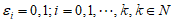 ,每个
,每个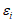 都有两种可能,
都有两种可能,
所以这种形式的自然数p共有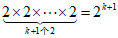 个结果,
个结果,
下证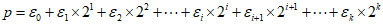
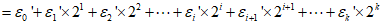
其中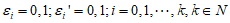 ,则
,则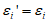
假设存在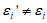 中,取i最大数为j,则
中,取i最大数为j,则
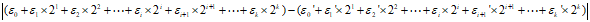
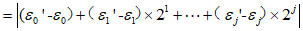
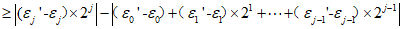
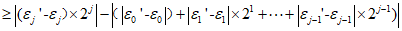
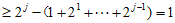
所以0≥1不可能。
综上,任意正整数p可唯一表示为
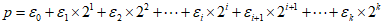
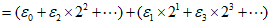
显然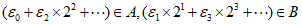 ,
,
满足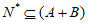 ,所以集合A,B互为”完美加法补集”.…………………11分
,所以集合A,B互为”完美加法补集”.…………………11分
(ii)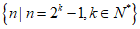 ………………14分
………………14分
(若用其他方法解题,请酌情给分)