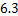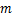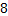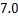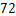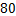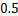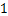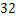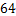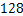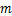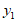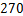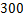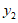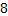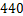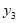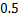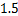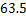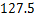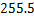本试卷共三道大题,28道小题。满分100分。考试时间120分钟。
一、选择题(本题共16分,每小题2分)
第1-8题均有四个选项,符合题意的选项只有一个.
1.下图是某个几何体的展开图,该几何体是
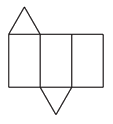
(A)三棱柱 (B)三棱锥 (C)圆柱 (D)圆锥
2.熔喷布,俗称口罩的”心脏”,是口罩中间的过滤层,能过滤细菌,阻止病菌传播.经测量,医用外科口罩的熔喷布厚度约为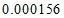 米,将
米,将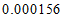 用科学记数法表示应为
用科学记数法表示应为
(A)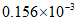 (B)
(B)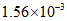 (C)
(C)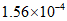 (D)
(D)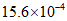
3.实数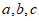 在数轴上的对应点的位置如图所示,则下列结论正确的是
在数轴上的对应点的位置如图所示,则下列结论正确的是
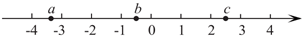
(A)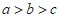 (B)
(B)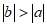 (C)
(C)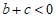 (D)
(D)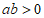
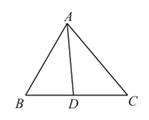
4.如图,在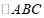 中,
中,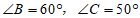 ,如果
,如果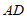 平分
平分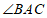 ,那么
,那么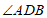 的度数是
的度数是
(A)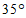 (B)
(B)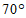 (C)
(C)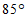 (D)
(D)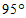
5.如果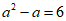 ,那么代数式
,那么代数式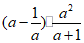 的值未
的值未
(A)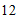 (B)
(B)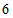 (C)
(C)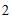 (D)
(D)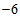
6.一组数据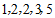 ,将这组数据中的每一个数都加上
,将这组数据中的每一个数都加上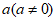 ,得到一组新数据
,得到一组新数据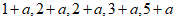 ,这两组数据的以下统计量相等的是
,这两组数据的以下统计量相等的是
(A)平均数 (B)众数 (C)中位数 (D)方差
7.如图,点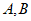 是
是 上的定点,点
上的定点,点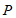 为优弧
为优弧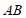 上的动点(不与点
上的动点(不与点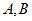 重合),在点
重合),在点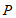 运动的过程中,以下结论正确的是
运动的过程中,以下结论正确的是
(A)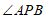 的大小改变
的大小改变
(B)点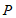 到弦
到弦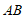 所在直线的距离存在最大值
所在直线的距离存在最大值
(C)线段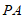 与
与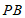 的长度之和不变
的长度之和不变
(D)图中阴影部分的面积不变
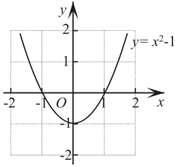
8.如图,抛物线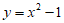 .将该抛物线在
.将该抛物线在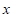 轴和
轴和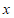 轴下方的部分记作
轴下方的部分记作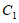 ,将
,将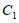 沿
沿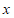 轴翻折记作
轴翻折记作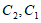 和
和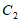 构成的图形记作
构成的图形记作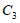 .关于图形
.关于图形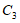 ,给出如下四个结论,其中错误的是
,给出如下四个结论,其中错误的是
(A)图形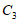 恰好经过4个整点(即横、纵坐标均为整数的点)
恰好经过4个整点(即横、纵坐标均为整数的点)
(B)图形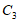 上任意一点到原点的距离都不超过1
上任意一点到原点的距离都不超过1
(C)图形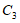 的周长大于
的周长大于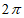
(D)图形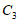 所围成的区域的面积大于2且小于
所围成的区域的面积大于2且小于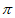
二、填空题(本题共16分,每小题2分)
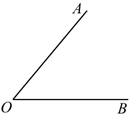
9.如图,已知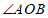 ,用量角器度量
,用量角器度量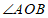 的度数为
的度数为
°.
10·不等式组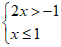 的所有整数解是
的所有整数解是
.
11.一个不透明的盒子中装有3个黄球,6个红球,这些球除了颜色外无其他差别.从中随机摸出一个球,恰好是黄球的概率为
.
12.小明把一副三角板摆放在桌面上,如图所示,其中边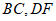 在同一条直线上可以得到
在同一条直线上可以得到
,依据是
.
13.如图,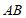 为
为 的直径,弦
的直径,弦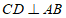 于点
于点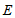 .如果
.如果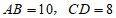 ,那么
,那么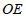 的长为
的长为
.
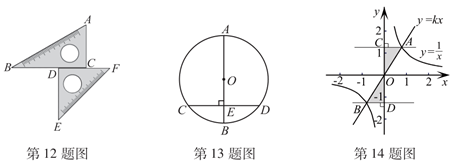
14. 如图,正比例函数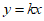 的图象和反比例函数
的图象和反比例函数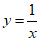 的图象交于
的图象交于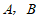 亮点,分别过点
亮点,分别过点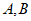 作
作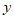 轴的垂线,垂足为点
轴的垂线,垂足为点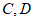 ,则
,则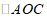 与
与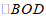 的面积之和为
的面积之和为
.
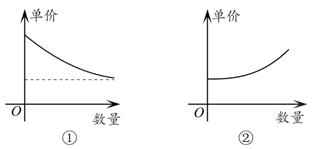
15.经济学家在研究市场供求关系时,一般用纵轴表示产品单价(自变量),而用横轴表示产品数量(因变量),下列两条曲线分别表示某种产品数量与单价之间的供求关系,一条表示厂商希望的供应曲线,另一条表示客户希望的需求曲线,其中表示客户希望的需求曲线的是
(填入序号即可).
16.小志自主创业,在网上经营一家水果店,销售的水果中有盒装草莓、荔枝、山竹,价格依次为40元/盒、60元/盒、80元/盒.为增加销量,小志对这三种水果进行促销:一次性购买水果的总价超过100元时,超过的部分打5折,每笔订单限购3盒.顾客支付成功后,小志会得到支付款的80%作为货款.
(1)顾客一笔订单购买了上述三种水果各一盒,则小志收到的货款是元
;
(2)小志在两笔订单中共售出原价180元的水果,则他收到的货款最少是
元
三、解答题(本题共68分,第17-24题,每小题5分,第25题6分,第26,28题,每小题7分,第27题8分)
17.下面是小文设计的”过圆外一点作圆的切线”的作图过程.
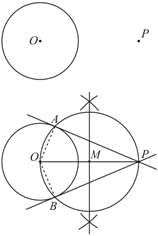
已知: 和圆外一点
和圆外一点 .
.
求作:过点 的
的 的切线.
的切线.
作法:①连接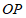 ;
;
②以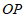 为直径作
为直径作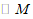 ,交
,交 于点
于点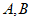 ;
;
③作直线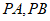 ;
;
所以直线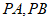 为
为 的切线.
的切线.
根据小文设计的作图过程,完成下面的证明.
证明:连接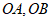 .
.
∵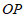 为
为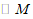 的直径,
的直径,
∴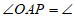
=
°
(
)(填推理的依据)
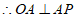 ,______
,______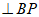 .
.
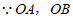 为
为 的半径,
的半径,
∴直线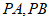 为
为 的切线(
的切线(
)(填推理的依据)
18.计算: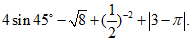
19.解分式方程: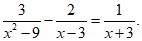
20.关于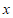 的方程
的方程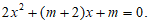
(1)求证:方程总有两个实数根;
(2)请你选择一个合适的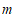 的值,使得方程的两个根都是整数,并求此时方程的根.
的值,使得方程的两个根都是整数,并求此时方程的根.
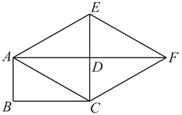
21.如图,矩形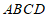 ,延长
,延长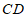 至点
至点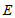 ,使
,使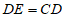 ,连接
,连接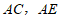 ,过点
,过点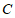 作
作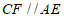 交
交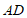 的延长线于点
的延长线于点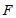 ,连接
,连接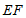 .
.
(1)求证:四边形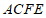 是菱形;
是菱形;
(2)连接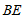 交
交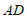 于点
于点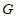 .当
.当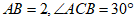 时,求
时,求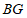 的长.
的长.
22.在平面直角坐标系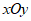 中,一次函数
中,一次函数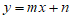 的图象与反比例函数
的图象与反比例函数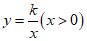 的图象交于点
的图象交于点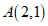 和点
和点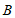 ,与
,与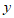 轴交于点
轴交于点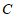 .
.
(1)求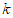 的值;
的值;
(2)如果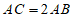 ,求一次函数的表达式.
,求一次函数的表达式.
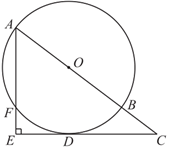
23.如图,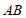 为
为 的直径,
的直径,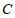 为
为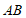 延长线上一点,
延长线上一点,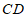 为
为 的切线,切点为
的切线,切点为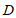 ,
,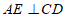 于点
于点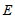 ,且
,且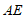 与
与 交于点
交于点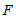 .
.
(1)求证:点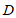 为
为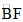 的中点;
的中点;
(2)如果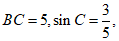 求
求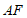 的长.
的长.
24.2020年3月至5月,某校开展了一系列居家阅读活动.学生利用”宅家”时光,在书海中遨游,从阅读中获得精神慰藉和自我提升.为了解学生居家阅读的情况,学校从七、八两个年级各随机抽取50名学生,进行了居家阅读情况调查.下面给出了部分数据信息:
a.两个年级学生平均每周阅读时长x(单位:小时)的频数分布直方图如下(数据分成4组: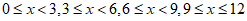 ):
):
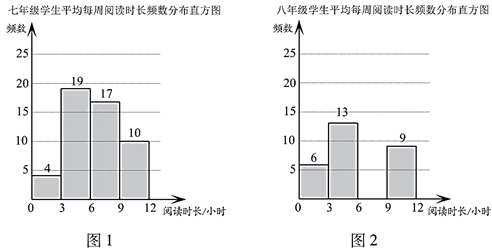
b.七年级学生平均每周阅读时长在6≤x<9这一组的是:
6 6 7 7 7 7 7 8 8 8 8 8 8 8 8 8 8
c.两个年级学生平均每周阅读时长的平均数、中位数、众数、方差如下:
平均数 | 中位数 | 众数 | 方差 | |
七年级 |
|
|
|
|
八年级 |
|
|
|
|
根据以上信息,回答下列问题:
(1)补全图2;
(2)写出表中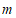 的值;
的值;
(3)返校后,学校计划将平均每周阅读时长不低于9小时的学生授予”阅读之星”称号.小丽说:”根据频数分布直方图中的数据信息,估计七年级约有20%的学生获得该称号,八年级约有18%的学生获得该称号,所以七年级获得该称号的人数一定比八年级获得该称号的人数多.”你认为她的说法
(填入”正确”或”错误”);
(4)请你结合数据对两个年级的居家阅读情况进行评价.
25.小腾的爸爸计划将一笔资金用于不超过10天的短期投资,针对这笔资金,银行专属客户经理提供了三种投资方案,这三种方案的回报如下:
方案一:每一天回报30元;
方案二:第一天回报8元,以后每一天比前一天多回报8元;
方案三:第一天回报0.5元,以后每一天的回报是前一天的2倍.
下面是小腾帮助爸爸选择方案的探究过程,请补充完整:
(1)确定不同天数所得回报金额(不足一天按一天计算),如下表:
天数 |
|
|
|
|
|
|
|
|
|
|
方案一 |
|
|
|
|
|
|
|
|
|
|
方案二 |
|
|
|
|
|
|
|
|
|
|
方案三 |
|
|
|
|
|
|
|
|
|
|
其中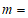
;
(2)计算累计回报金额,设投资天数为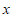 (单位:天),所得累计回报金额是
(单位:天),所得累计回报金额是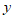 (单位:元),于是得到三种方案的累计回报金额)。
(单位:元),于是得到三种方案的累计回报金额)。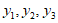 与投资天数
与投资天数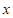 的几组对应值:
的几组对应值:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中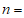
;
(3)在同一平面直角坐标系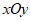 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点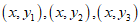 ,并画出
,并画出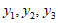 的图象;
的图象;
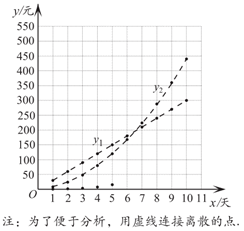
(4)结合图象,小腾给出了依据不同的天数而选择对应方案的建议:
26.在平面直角坐标系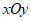 中,抛物线
中,抛物线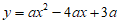 与
与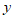 轴交于点
轴交于点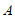 .
.
(1)求点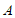 的坐标(用含
的坐标(用含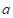 的式子表示);
的式子表示);
(2)求抛物线与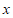 轴的交点坐标;
轴的交点坐标;
(3)已知点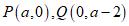 ,如果抛物线与线段
,如果抛物线与线段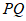 恰有一个公共点,结合函数图象,求
恰有一个公共点,结合函数图象,求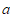 的取值范围.
的取值范围.
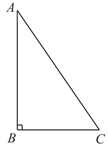
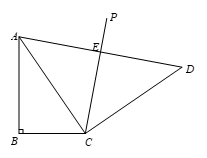
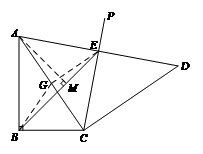
27.如图,在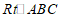 中,
中,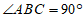 ,将
,将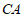 绕点
绕点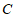 顺时针旋转
顺时针旋转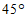 ,得到
,得到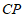 ,点
,点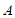 关于直线
关于直线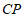 的对称点为
的对称点为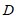 ,连接
,连接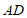 交直线
交直线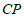 于点
于点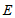 ,连接
,连接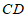 .
.
(1)根据题意补全图形;
(2)判断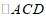 的形状,并证明;
的形状,并证明;
(3)连接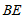 ,用等式表示线段
,用等式表示线段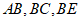 之间的数量关系,并证明.
之间的数量关系,并证明.
温馨提示:在解决第(3)问的过程中,如果你遇到困难,可以参考下面几种解法的主要思路.
解法1的主要思路:
延长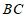 至点
至点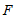 ,使
,使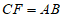 ,连接
,连接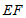 ,可证
,可证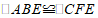 ,再证
,再证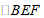 是等腰直角三角形.
是等腰直角三角形.
解法2的主要思路:
过点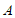 作
作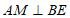 于点
于点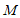 ,可证
,可证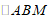 是等腰直角三角形,再证
是等腰直角三角形,再证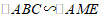 .
.
解法3的主要思路:
过点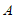 作
作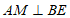 于点
于点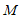 ,过点
,过点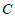 作
作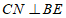 于点
于点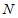 ,设
,设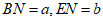 用含
用含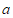 或
或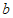 的式子表示
的式子表示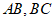 .
.
······.
28.过直线外一点且与这条直线相切的圆称为这个点和这条直线的点线圆.特别地,半径最小的点线圆称为这个点和这条直线的最小点线圆.在平面直角坐标系 中,点
中,点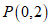 .
.
(1)已知点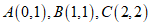 ,分别以
,分别以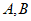 为圆心,1为半径作
为圆心,1为半径作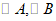 ,以
,以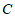 为圆心,2为半径作
为圆心,2为半径作 ,其中是点
,其中是点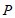 和
和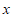 轴的点线圆的是
轴的点线圆的是
;
(2)记点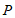 和
和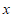 轴的点线圆为
轴的点线圆为 ,如果
,如果 与直线
与直线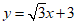 没有公共点,求
没有公共点,求 的半径
的半径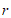 的取值范围;
的取值范围;
(3)直接写出点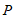 和直线
和直线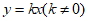 的最小点线圆的圆心的横坐标
的最小点线圆的圆心的横坐标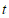 的取值范围.
的取值范围.
【试题答案】
一、选择题(本题共16分,每小题2分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | A | C | D | C | B | D | B | C |
二、填空题(本题共16分,每小题2分)
9. 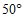 10. 0,1 11.
10. 0,1 11. 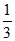 12. AC∥DE;内错角相等,两直线平行 13. 3 14. 1 15. ① 16. 112;128
12. AC∥DE;内错角相等,两直线平行 13. 3 14. 1 15. ① 16. 112;128
三、解答题(本题共68分,第17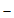 24题,每小题5分,第25题6分,第26,28题,每小题7分,第27题8分)
24题,每小题5分,第25题6分,第26,28题,每小题7分,第27题8分)
17.证明:连接OA,OB.
∵OP为⊙E的直径,
∴∠OAP=∠OBP=90°.
(直径所对的圆周角是直角).
∴OA⊥AP,OB⊥BP.
∵OA,OB为⊙O的半径,
∴直线PA,PB为⊙O的切线.(经过半径的外端,并且垂直于这条半径的直线是圆的切线).……5分
18.解:原式=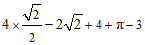
=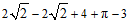 …4分
…4分
=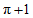 .……5分
.……5分
19.解: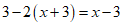 .
.
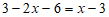 .…..2分
.…..2分
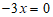 .
.
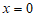 .……4分
.……4分
经检验,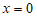 是原方程的解.
是原方程的解.
∴原方程的解是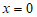 .……5分
.……5分
20.解:(1)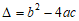
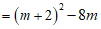
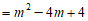
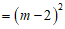 ≥0.……1分
≥0.……1分
∴原方程总有两个实数根.2分
(2)当m=0时,原方程化为2x2+2x=0.
解得x1=0,x2=-1.……5分(m的值不唯一,满足题意解答正确即可)
21.(1)证明:∵CF∥AE,
∴∠1=∠2.
在△ADE与△FDC中,
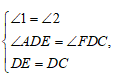
∴△ADE≌△FDC.
∴AE=CF.……1分
∴四边形ACFE是平行四边形.
∵四边形ABCD是矩形,
∴∠ADC=90°.
∴CE⊥AF.
∴四边形ACFE是菱形.…3分
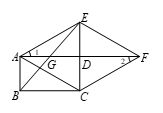
(2)解:∵矩形ABCD中,
∴∠ABC=∠BCD=90°.
CD=AB=2.
∵∠ACB=30°,
∴BC=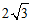 ,EC=4.
,EC=4.
在Rt△BCE中,
BE= .…4分
.…4分
∵GD∥BC,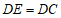 ,
,
∴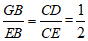 .
.
∴BG=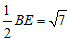 .……5分
.……5分
22.解:(1)∵反比例函数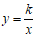 的图象经过
的图象经过
点A(2,1),
∴k=2……2分
(2)分别过点A,B作AD,BE垂直y轴于点D,E.
∵A(2,1),
∴AD=2.
情况1:当点B在线段AC上时.
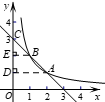
∵AC=2AB,∴BE=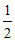 AD=1.
AD=1.
∴B(1,2).
∵一次函数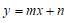 过点A(2,1),B(1,2),
过点A(2,1),B(1,2),
可得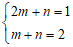 ,
,
解得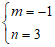 .
.
∴一次函数表达式为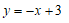 .
.
情况2:当点B在线段AC反向延长线上时.
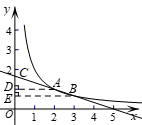
∵AC=2AB,
∴BE=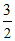 AD=3.
AD=3.
∴B(3,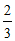 ).
).
∵一次函数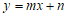 过点
过点
A(2,1),B(3,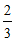 ),
),
可得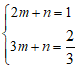 ,
,
解得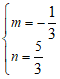 .
.
∴一次函数表达式为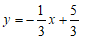 .……5分
.……5分
23.解:(1)连接OD,BF相交于点G.
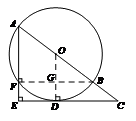
∵CD为⊙O的切线,
∴∠ODC=90°.……1分
∵AB为⊙O的直径,
∴∠AFB=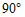 =
=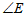 .
.
∴BF∥EC.
∴∠OGB=∠ODC=90°.
即OD⊥BF.
∴D为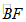 的中点.……2分
的中点.……2分
(2)在Rt△COD中,sinC=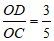 ,
,
设⊙O的半径为r.
∴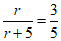 .
.
∴r=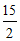 .……3分
.……3分
由(1)得∠ABF=∠C,
∴sin∠ABF=sinC=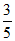 .…4分
.…4分
在Rt△ABF中,
sin∠ABF=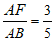 ,
,
∴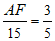 .
.
∴AF=9.……5分
24.(1)正确补全图形;……1分
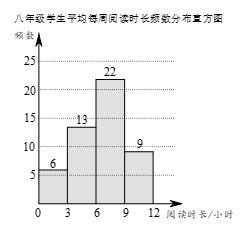
(2)6.5;……2分
(3)错误.……3分
(4)答案不唯一,理由支持结论即可.……5分
25.解:(1)m=256;(2)n=511.5………2分
(3)正确画出函数图象:
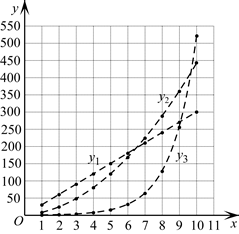 ………3分
………3分
(4)如果爸爸投资天数不超过6天时,应该选择方案一;如果爸爸投资天数在7到9天时,应该选择方案二;如果爸爸投资天数为10天时,应该选择方案三.…6分
26.解:(1)令x=0,则y=3a.
∴点A的坐标为(0,3a).………………………………………………1分
(2)令y=0,则ax2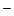 4ax+3a=0.…………………………………………2分
4ax+3a=0.…………………………………………2分
∵a≠0,∴解得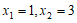 .
.
∴抛物线与x轴的交点坐标分别为(1,0),(3,0).…………4分
(3)①当a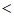 0时,
0时,
可知3a≥a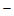 2.解得a≥-1.
2.解得a≥-1.
∴a的取值范围是-1≤a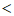 0.
0.
②当a>0时,由①知a≥-1时,点Q始终在点A的下方,所以抛物线与线段PQ恰有一个公共点时,只要1≤a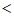 3即可.
3即可.
综上所述,a的取值范围是-1≤a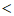 0或1≤a
0或1≤a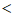 3………7分
3………7分
 .解:(1)正确补全图形:
.解:(1)正确补全图形:
 ……………………………2分
……………………………2分
(2)△ACD是等腰直角三角形;…………………………………3分
证明:∵将CA绕点C顺时针旋转45°,
∴∠ACP=45°.
∵点D与A关于直线CP对称,
∴∠DCP=∠ACP=45°,AC=CD.
∴∠ACD=90°.
∴△ACD是等腰直角三角形.………………………………4分
(3)AB+BC=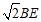 ;………………………………………………5分
;………………………………………………5分
解法1证明:延长BC至点F,使CF=AB,连接DF,EF.
∵△ACD是等腰直角三角形,AE=DE,
∴AE=CE,∠AEC=90°.
∵∠ABC=90°,
∴∠BAE+∠BCE=180°.
∵∠FCE+∠BCE=180°,
∴∠BAE=∠FCE.
∴△ABE≌△CFE.…………………………………………6分
∴BE=FE,∠1=∠2.
∴∠2+∠3=∠1+∠3=90°.
即∠BEF=90°.
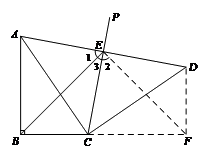
∴△BEF是等腰直角三角形.……………………………7分
∴BC+CF=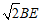 .
.
即AB+BC=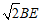 .……………………………………8分
.……………………………………8分
解法2证明:过点A作AM⊥BE于点M,取AC中点G,连接GB,GE.
设∠GBE=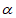 ,∠ABG=
,∠ABG=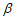 ,
,
∵∠ABC=∠AEC=90°,
∴AG=BG=EG=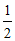 AC.
AC.
∴∠ABG=∠BAC=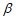 ,∠GBE=∠GEB=
,∠GBE=∠GEB=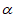 .
.
在△BGE中,
∵∠GBE+∠BGE+∠BEG=180°,
∴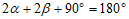 .
.
∴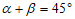 .
.
即∠ABE=45°.……………………………………6分
(或根据圆的定义判断A,B,C,E在以点G为圆心的圆上,根据同弧CE所对圆周角相等,证明∠ABE=45°)
∵∠AMB=90°,
∴∠BAM=∠CAE=45°.
∴∠BAC=∠MAE.
∵∠ABC=∠AME=90°,
∴△ABC∽△AME.…………………………………………7分
∴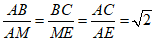 .
.
∴BC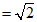 ME.
ME.
又∵AB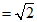 BM.
BM.
∴AB+BC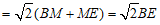 .……………………8分
.……………………8分
解法3证明:过点A作AM⊥BE于点M,过C作CN⊥BE于点N,
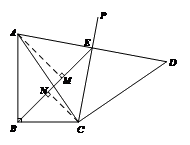
∴∠AME=∠CNE=90°.
即∠MAE+∠AEM=90°.
∵∠MEC+∠AEM=90°.
∴∠MAE=∠MEC.
∵AE=CE,
∴△AME≌△ECN.……………………………………6分
∴AM=EN.
同解法2,可证∠ABM=∠CBM=45°.……………………………7分
设BN=a,EN=b
∴BC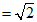 a,AB
a,AB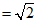 b.
b.
∴AB+BC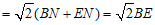 .……………………8分
.……………………8分
(说明:三条线段数量关系写为: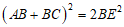 等其他等式如果正确也给分)
等其他等式如果正确也给分)
28.解:(1)⊙A,⊙C;………………………………………………………………2分
(2)如图1,⊙D1过点P,且与x轴和直线y=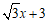 都相切.
都相切.
此时⊙D1的半径r=1.
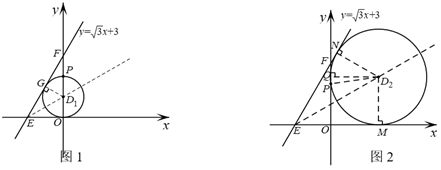
如图2,⊙D2过点P,且与x轴和直线y=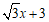 都相切.切点分别为M,N,连接D2M,D2N,D2P,过点D2作D2Q⊥y轴于点Q.
都相切.切点分别为M,N,连接D2M,D2N,D2P,过点D2作D2Q⊥y轴于点Q.
设D2M=r,
∴D2P=D2M=r.
易证OQ=D2M=r.
∴PQ=r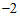 .
.
∵∠MEN=60°,
∴∠D2EM=30°.
∴EM=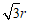 .
.
∴OM=D2Q=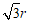
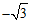 .
.
根据勾股定理可以得到:D2P2=D2Q2+PQ2,
即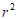 =
=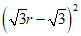 +
+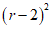 .
.
解得r1=1(舍),r2=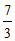 .
.
∴1<r<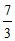 .………………………………………………………5分
.………………………………………………………5分
(3)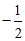 ≤x
≤x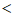 0或0
0或0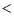 x≤
x≤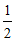 .………………………………………………………7分
.………………………………………………………7分